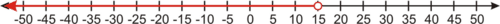Section: 不平等 | 1.9 不平等

Section outline

Introduction
::导言

An inequality is a relation between two expressions that are not equal. Inequality signs include ≠ (not equal to), > (greater than), ≥ ( greater than or equal to), < (less than), and ≤ ( less than or equal to). These can be used to describe and solve situations such as the following:
::不平等是两个不平等的表达形式之间的关系。不平等的迹象包括 (不等于), > (大于), (大于或等于), < (低于), 和 (不等于或等于) 。这些可以用来描述和解决以下情况:

Ms. Jain wants to buy identical boxes of art supplies for her 25 students. If she can spend no more than $375 on art supplies, what inequality describes the price can she afford for each individual box of supplies?
::Jain女士想为25名学生购买一箱相同的艺术用品,如果她花在艺术用品上的费用不超过375美元,那么她能为每盒用品支付多少价钱呢?

Expressing Solutions of an Inequality
::表达不平等的解决办法

The solution of an inequality can be expressed in four different ways:
::解决不平等的办法可以用四种不同的方式表达:

1. Inequality notation. The answer is simply expressed as $\begin{aligned} x < 15 \end{aligned}$ .
::1. 不平等表示:答案仅以x<15表示。

2. Set notation . The answer is expressed as a set: $\begin{aligned} {x | x < 15} \end{aligned}$ . The brackets indicate a set, and the vertical line means “such that,” so we read this expression as “the set of all values of $\begin{aligned} x \end{aligned}$ such that $\begin{aligned} x \end{aligned}$ is a real number less than 15.”
::2. 设置符号。答案以一组表示 : {xx < 15}。括号表示一组,垂直线表示 " 例如, " ,因此我们将这一表达式解读为 " x 所有数值的组,使 x 实际数字小于15。 "

3. Interval notation. This uses brackets to indicate the range of values in the solution. For example, the answer to our problem would be expressed as $\begin{aligned} (- \infty, 15) \end{aligned}$ , meaning “the interval containing all the numbers from $\begin{aligned} - \infty \end{aligned}$ to 15, but not actually including $\begin{aligned} - \infty \end{aligned}$ or 15.”
::3. 中间符号:使用括号来表示解决方案中的数值范围,例如,我们问题的答案将以(,15)表示,意思是 " 包含%至15之间所有数字的间隔,但实际上不包括或15。 "

a) Square or closed brackets “[” and “]” indicate that the number next to the bracket is included in the solution set .
:a) 方括号或封闭括号“[”和“]”表示括号旁边的数字包括在一套解决办法中。

b) Round or open brackets “(” and “)” indicate that the number next to the bracket is not included in the solution set. When using infinity and negative infinity ( $\begin{aligned} \infty \end{aligned}$ and $\begin{aligned} - \infty \end{aligned}$ ), we always use open brackets because infinity isn’t an actual number and so it can never be included in an interval.
:b) 圆括号或括号 " ( " ) " 和 " ( " ) " )表示括号旁边的数字没有包括在一套解决办法中,在使用无限性和负无限性(和)时,我们总是使用括号,因为无限性不是实际数字,因此它永远不能包括在一个间隔内。

4. Solution graph. This shows the solution on the real number line. A closed circle on a number indicates that the number is included in the solution set, while an open circle indicates that the number is not included in the set. For our example, the solution graph is:
::4. 解析图:此图显示实际数字线上的解析法。数字上的封闭圆表示数字包含在解析套件中,而开放圆则表示数字不包括在解析套件中。例如,解析图是:

The following video reviews these four types of notation:
::以下视频回顾这四类标记:

Identify the Number of Solutions of an Inequality
::确定不平等解决方案的数量

Inequalities can have:
::不平等可以有:

A set that has an infinite number of solutions.
::一组有无限数的解决方案。

A set that has a finite number of solutions.
::一组有一定数量的解决办法。

No solutions.
::无解决办法。

I nequalities often have an infinite number of solutions, at least in theory. For example, the inequality $\begin{aligned} \frac{5 x - 1}{4} > - 2 (x + 5) \end{aligned}$ has the solution $\begin{aligned} x > - 3 \end{aligned}$ . This solution says that all real numbers greater than -3 make this inequality true, and there are infinitely many such numbers.
::不平等往往有无限数量的解决办法,至少在理论上是如此。比如,不平等 5x-142(x+5) 就有了解决方案 x3 。这个解决方案指出,所有实际数字都大于 - 3 使这种不平等成为现实,而且此类数字也无穷无尽。

However, in real life, sometimes we are trying to solve a problem that can only have positive integer answers, because the answers describe numbers of discrete objects.
::然而,在现实生活中,有时我们试图解决一个只能有正整数答案的问题,因为答案描述了离散物体的数量。

For example, suppose you are trying to figure out how many $8 pens you can buy if you want to spend less than $50. An inequality to describe this situation would be $\begin{aligned} 8 x < 50 \end{aligned}$ , and if you solved that inequality you would get $\begin{aligned} x < \frac{50}{8} \end{aligned}$ , or $\begin{aligned} x < 6.25 \end{aligned}$ .
::例如,假设您正在试图弄清楚如果想要花费不到50美元,您可以买多少笔8美元。描述这种情况的不平等程度为8x<50,如果解决了不平等,您将得到 x<508 或 x<6.25。

But could you really buy any number of pens as long as it’s less than 6.25? No; you couldn’t buy 6.1 pens, or -5 pens, or any other fractional or negative number of pens. So if we wanted to express our solution in set notation, we couldn’t express it as the set of all numbers less than 6.25, or $\begin{aligned} {x | x < 6.25} \end{aligned}$ . Instead, the solution is just the set containing all the nonnegative whole numbers less than 6.25, or {0, 1, 2, 3, 4, 5, 6}. When we’re solving a real-world problem dealing with discrete objects like pens, our solution set will often be a finite set of numbers instead of an infinite interval.
::但是,只要小于6.25,你真的能买到任何数量的笔吗? 不;你不能买到6.1支笔,或者5支笔,或者任何其他的分数或负数笔。因此,如果我们想用设定符号来表达我们的解决方案,我们就不能把它表达为所有数字少于6.25的一组,或者{xx < 6.25}。相反,解决方案只是包含所有非负数不到6.25的整数,或者{0,1,2,3,4,4,5,6}。当我们解决与诸如笔等离散物体有关的现实世界问题时,我们的解决方案往往只是一组有限的数字,而不是无限的间隔。

An inequality can also have no solutions at all. For example, consider the inequality $\begin{aligned} x - 5 > x + 6 \end{aligned}$ . When we subtract $\begin{aligned} x \end{aligned}$ from both sides, we end up with $\begin{aligned} - 5 > 6 \end{aligned}$ , which is not true for any value of $\begin{aligned} x \end{aligned}$ . We say that this inequality has no solution.
::不平等也不可能有任何解决办法。例如,考虑不平等 x-5>x+6 。当我们从两边减去 x 时,我们最终会得到 - 5>6 。这对x 的任何价值来说都是不正确的。我们说,这种不平等是没有解决办法的。

The opposite can also be true. If we flip the inequality sign in the above inequality, we get $\begin{aligned} x - 5 < x + 6 \end{aligned}$ , which simplifies to $\begin{aligned} - 5 < 6 \end{aligned}$ . That’s always true no matter what $\begin{aligned} x \end{aligned}$ is, so the solution to that inequality would be all real numbers , or $\begin{aligned} (- \infty, \infty) \end{aligned}$ .
::反之亦然。如果我们翻转上述不平等中的不平等标志,我们就会得到x-5<x+6,它简化为~5<6。这始终是事实,不管x是什么,因此解决不平等的办法都是真实数字,或者(,,)。

Examples
::实例

Example 1
::例1

Describe what the following solutions in interval notation mean:
::说明间距符号中的下列解决办法的含义:

a) [-4, 6]
:a) [-4、6]

Solution:
::解决方案 :

The solution is all numbers between -4 and 6, including -4 and 6.
::解决办法是在-4和6之间的所有数字,包括-4和6。

b) (8, 24)
:b) (8,24)

Solution:
::解决方案 :

The solution is all numbers between 8 and 24, not including the numbers 8 and 24.
::解决办法是8到24之间的所有数字,不包括8和24。

c) [3, 12)
:c) [3、12]

Solution:
::解决方案 :

The solution is all numbers between 3 and 12, including 3 but not including 12.
::解决办法是3到12之间的所有数字,包括3个,但不包括12个。

d) $\begin{aligned} (- 10, \infty) \end{aligned}$
:d) (-10,)

Solution:
::解决方案 :

The solution is all numbers greater than -10, not including -10.
::解决方案的数值均大于 -10, 不包括 -10 。

e) $\begin{aligned} (- \infty, \infty) \end{aligned}$
::e) (,)

Solution:
::解决方案 :

The solution is all real numbers.
::解决办法都是真实的数字。

Example 2
::例2

Solve the following inequality. Write the solution in inequality and set notation.
::解决以下不平等问题,写出解决不平等问题的办法,并设置符号。

$\begin{aligned} - 2 x < 12 \end{aligned}$
Solution:
::- 2x < 12 解答 :

Divide both sides of the inequality by $\begin{aligned} - 2 \end{aligned}$ . Remember that the inequality sign needs to be switched from less than to greater than (or from greater than to less than) when you multiply or divide both sides of an inequality by a negative number:
::将不平等的两边除以-2。记住,当不平等的两边增加或除以负数时,不平等的标志需要从小于(或从大于)改为大于(或从小于)时,不平等的标志需要从小于(或从大于)改为大于(或小于),因为不平等的两边增加或除以负数:

$\begin{aligned} \frac{- 2 x}{- 2} & > \frac{12}{- 2} \\ x & > - 6 \end{aligned}$
In set notation, the solution is $\begin{aligned} {x | x > - 6} \end{aligned}$ .
::-2x-2>12 -2x6 在设定符号中, 解决方案是 {xx6} 。

Example 3
::例3

Solve the inequality below. Write the solution in inequality and set notation.
::解决以下的不平等问题,写出解决不平等问题的办法,并设置符号。

$\begin{aligned} 8 - 4 x \geq 2 (3 x - 11) \end{aligned}$
Solution:
::8-4x=2(3x-11) 溶液:

Step 1: Distribute the 2 on the right side of the inequality:
::第1步:在不平等的右侧分配2:

$\begin{aligned} 8 - 4 x & \geq 2 (3 x - 11) \\ 8 - 4 x & \geq 6 x - 22 \end{aligned}$

::8-4x=2(3x-11)8-4x-6x-22

Step 2: Collect the numbers on one side of the inequality and all the $\begin{aligned} x \end{aligned}$ terms to the other side of the inequality:

::第2步:收集不平等一方的数字和不平等另一方的所有x条件:

$\begin{aligned} 8 - 8 - 4 x - 6 x & \geq 6 x - 6 x - - 22 - 8 \\ - 10 x & \geq - 30 \end{aligned}$
Step 3: Divide both sides of the inequality by $\begin{aligned} - 10 \end{aligned}$ and switch the inequality sign:

::8 - 8 - 4x- 6x6x6x6x 22 - 8 - 10x 30 Step 3: 将不平等的两边除以- 10, 并改变不平等的标志 :

$\begin{aligned} \frac{- 10 x}{- 10} & \leq \frac{- 30}{- 10} \\ x & \leq 3 \end{aligned}$

::- 10x-1030-10x3

In set notation, the solution is $\begin{aligned} {x | x \leq 3} \end{aligned}$ .
::在设定符号中, 解决方案是 {xx} 。

Example 4

::例4

In order to get a bonus this month, Lalit must sell at least 120 newspaper subscriptions. He sold 85 subscriptions in the 1st three weeks of the month. How many subscriptions must Lalit sell in the last week of the month?
::为了获得本月的奖金,Lalit必须卖掉至少120份报纸订阅费。他在这个月的第一个星期卖了85份订阅费。Lalit必须在这个月的最后一周卖出多少订阅费?

Solution:
::解决方案 :

Let $\begin{aligned} x = \end{aligned}$ the number of subscriptions Lalit sells in the last week of the month. The total number of subscriptions for the month must be greater than 120, so we write $\begin{aligned} 85 + x \geq 120 \end{aligned}$ . We solve the inequality by subtracting 85 from both sides: $\begin{aligned} x \geq 35 \end{aligned}$ .
::Let x = Lalit 在当月最后一周销售的订阅数量。该月的订阅总数必须超过120个, 所以我们写85+x 120。我们从双方减去85个, 解决不平等问题 : x% 35 。

Therefore , Lalit must sell 35 or more subscriptions in the last week to get his bonus.
::因此,Lalit必须在上周出售35个或更多的订阅费,以获得奖金。

To check the answer, we see that $\begin{aligned} 85 + 35 = 120 \end{aligned}$ . If he sells 35 or more subscriptions, the total number of subscriptions he sells that month will be 120 or more.
::为了检查答案,我们可以看到85+35=120。如果他出售35个或更多的订阅,那么他该月销售的订阅总数将是120个或120个以上。

Example 5

::例5

A group of Class VI students is trying to raise at least $650 this summer. How many boxes of erasers (each box has only 2 erasers) must they sell at $4.50 per box in order to reach their goal?
::今年夏天,一群六年级学生想募集至少650美元。为了达到他们的目标,他们必须卖出多少箱橡皮纸(每个盒子只有两个橡皮纸 ) , 每箱4.50美元?

Solution:
::解决方案 :

Let $\begin{aligned} x = \end{aligned}$ number of boxes sold. Then the inequality describing this problem is $\begin{aligned} 4.50 x \geq 650 \end{aligned}$ .
::Let x= 售出箱数。然后描述这一问题的不平等度是 4. 50x650 。

We solve the inequality by dividing both sides by 4.50: $\begin{aligned} x \geq 144.44 \end{aligned}$ .
::我们通过将双方除以4.50:x144.44来解决不平等问题。

We round up the answer to 145, since only whole boxes can be sold.
::我们找回145个答案因为只有整个箱子可以卖掉

Therefore, the group of Class VI students must sell at least 145 boxes.
::因此,六年级学生必须出售至少145箱。

If we multiply 145 by $4.50, we obtain $652.50. So if the group sells more than 144 boxes, they will raise more than $650. But if they sell 144 boxes, they will raise only $648, which is not enough. So they must indeed sell at least 145 boxes.
::如果我们把145乘以4.5乘以4.5美元,我们就会得到652.50美元。因此,如果该集团出售144箱以上,它们将筹集650美元以上。但如果它们出售144箱,它们只筹集648美元,这是不够的。因此它们必须至少出售145箱。

Example 6

::例6

The width of a rectangle is 20 cm. What must the length be if the perimeter is at least 180 cm?
::矩形宽度为 20 厘米。如果周边至少为 180 厘米, 长度必须是什么 ?

Solution:
::解决方案 :

Let $\begin{aligned} x = \end{aligned}$ length of the rectangle. The formula for perimeter is
::x= 矩形的长度。圆周的公式是

$\begin{aligned} Perimeter = 2 \times length + 2 \times width \end{aligned}$

::半径=2x长+2x宽

Since the perimeter must be at least 180 cm, we have $\begin{aligned} 2 x + 2 (20) \geq 180 \end{aligned}$ .
::由于周界必须至少180厘米,我们有2x+2(20)-180。

Simplify: $\begin{aligned} 2 x + 40 \geq 180 \end{aligned}$
::简化: 2x+40-180

Subtract 40 from both sides: $\begin{aligned} 2 x \geq 140 \end{aligned}$
::双方减40:2x140

Divide both sides by 2: $\begin{aligned} x \geq 70 \end{aligned}$
::将两边除以 2 : x / 70

Therefore, the length must be at least 70 cm.
::因此,长度必须至少为70厘米。

If the length is at least 70 cm and the width is 20 cm, then the perimeter is at least $\begin{aligned} 2 (70) + 2 (20) = 180 c m \end{aligned}$ .
::如果长度至少为70厘米,宽度为20厘米,则周界至少为2(270+2(20)=180厘米。

The following video provides real-world applications of solving inequalities:
::以下影片提供解决不平等的现实应用:

Review
::回顾

Solve each inequality. Give the solution in inequality notation and interval notation.
::解决每一种不平等,提供不平等的标记和间隙标记的解决方案。

1. $\begin{aligned} x + 15 < 12 \end{aligned}$
::1. x+15 < 12

2. $\begin{aligned} x - 4 \geq 13 \end{aligned}$
::2. x-413

3. $\begin{aligned} 9 x > - \frac{3}{4} \end{aligned}$
::3. 9x______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

4. $\begin{aligned} - \frac{x}{15} \leq 5 \end{aligned}$
::4. - 155-5

5. $\begin{aligned} 620 x > 2400 \end{aligned}$
::5. 620x>2400

6. $\begin{aligned} \frac{x}{20} \geq - \frac{7}{40} \end{aligned}$
::6. x20=740

7. $\begin{aligned} \frac{3 x}{5} > \frac{3}{5} \end{aligned}$
::7. 3x5>35

8. $\begin{aligned} x + 3 > x - 2 \end{aligned}$
::8. x+3>x-2

Solve each inequality. Give the solution in inequality notation and set notation.
::解决每一种不平等,给出不平等的标记和设置标记的解决方法。

9. $\begin{aligned} x + 17 < 3 \end{aligned}$
::9. x+17 <3

10. $\begin{aligned} x - 12 \geq 80 \end{aligned}$
::10 - 12- 1980

11. $\begin{aligned} - 0.5 x \leq 7.5 \end{aligned}$
::11.-0.5x=7.5

12. $\begin{aligned} 75 x \geq 125 \end{aligned}$
::12. 75x=125

13. $\begin{aligned} \frac{x}{- 3} > - \frac{10}{9} \end{aligned}$
::13. x-3109

14. $\begin{aligned} \frac{x}{- 15} < 8 \end{aligned}$
::14. x-15 < 8

15. $\begin{aligned} \frac{x}{4} > \frac{5}{4} \end{aligned}$
::15. x4>54

16. $\begin{aligned} 3 x - 7 \geq 3 (x - 7) \end{aligned}$
::16. 3x-73(x-7)

Solve the following inequalities, give the solution in set notation, and show the solution graph:
::解决以下不平等问题,在设定符号时给出解决方案,并显示解决方案图:

17. $\begin{aligned} 4 x + 3 < - 1 \end{aligned}$
::17. 4x+3=1

18. $\begin{aligned} 2 x < 7 x - 36 \end{aligned}$
::18. 2x < 7x-36

19. $\begin{aligned} 5 x > 8 x + 27 \end{aligned}$
::19. 5x8x+27

20. $\begin{aligned} 5 - x < 9 + x \end{aligned}$
::20. 5-x<9+x

21. $\begin{aligned} 4 - 6 x \leq 2 (2 x + 3) \end{aligned}$
::21. 4-6x=2(2x+3)

22. $\begin{aligned} 5 (4 x + 3) \geq 9 (x - 2) - x \end{aligned}$
::22. 5(4x+3)9(x-2)-x

23. $\begin{aligned} 2 (2 x - 1) + 3 < 5 (x + 3) - 2 x \end{aligned}$
::23. 2(2(2x-1-1)+3 <5(x+3)-2x

24. $\begin{aligned} 8 x - 5 (4 x + 1) \geq - 1 + 2 (4 x - 3) \end{aligned}$
::24. 8x-5( 4x+1) 1+2( 4x-3)

25. $\begin{aligned} 2 (7 x - 2) - 3 (x + 2) < 4 x - (3 x + 4) \end{aligned}$
::25. 2(7x-2)-3(x+2) <4x-(3x+4)

26. $\begin{aligned} \frac{2}{3} x - \frac{1}{2} (4 x - 1) \geq x + 2 (x - 3) \end{aligned}$
::26. 23x-12(4x-1-1)x+2(x-3)

27. At the Delhi Zoo, you can pay either $22 for the entrance fee or $71 for the yearly pass, which entitles you to unlimited admission.
::27. 在德里动物园,您可以支付22美元的入场费,也可以支付71美元的年假,这可使您获得无限制的入场许可。

a) At most, how many times can you enter the zoo for the $22 entrance fee before spending more than the cost of a yearly membership?
:a) 最多,在花费超过每年会员费用之前,你有多少次可以进入动物园收取22美元的入场费?

b) Are there infinitely many or finitely many solutions to this inequality?
:b) 对这种不平等是否有无限多或有限的许多解决办法?

28. Prateek's scores for four tests were 82, 95, 86, and 88. What will he have to score on his 5th and last test to average at least 90 for the term?
::28. 普尔提的四次考试得分是82、95、86和88,

Review (Answers)
::回顾(答复)

Please see the Appendix.
::请参看附录。

Section outline

Introduction ::导言

Expressing Solutions of an Inequality ::表达不平等的解决办法

Examples ::实例

Review ::回顾

Review (Answers) ::回顾(答复)

Introduction
::导言

Expressing Solutions of an Inequality
::表达不平等的解决办法

Examples
::实例

Review
::回顾

Review (Answers)
::回顾(答复)