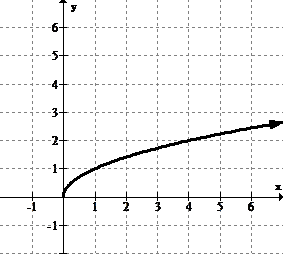Section: 最大和最低 | 2.3 最大和最低

Section outline

Introduction
::导言

Roller Coaster

When riding a roller coaster, you will always reach one point that is the absolute highest off the ground. There are usually many other places that reach fairly high—just not as high as that one. How do you identify and distinguish between these different peaks in a precise way?
::当骑过山车时,你总是会达到一个绝对最高点。通常还有其他很多地方到达相当高的地方,只是没有那个那么高。你如何精确地辨别和区分这些不同的山峰呢?

Local and Absolute Maximum and Minimum
::本地和绝对最大和最低

Local extrema and relative extrema are synonyms that refer to the points with the $\begin{aligned} y \end{aligned}$ -values that are the highest or lowest $\begin{aligned} y \end{aligned}$ -values on a local neighborhood of the domain of a function.
::本地 extrema 和相对 extrema 是同义词, 指函数域内某个地方附近的 Y 值最高或最低 y 值的点。

Global extrema and absolute extrema are synonyms that refer to the points with the $\begin{aligned} y \end{aligned}$ -values that are either the highest or the lowest $\begin{aligned} y \end{aligned}$ -values on the entire domain of the function.
::Global extrema 和绝对 extrema 是同义词, 指函数整个域最高或最低 y 值的 y 值点。

One way to identify local extrema is by looking at a graph. The local minimum values are all the $\begin{aligned} y \end{aligned}$ -values on the graph that appear as a valley. The local maximum values are all the $\begin{aligned} y \end{aligned}$ -values on the graph that appear as the top of a hill. The absolute minimum is the smallest $\begin{aligned} y \end{aligned}$ -value on the graph. The absolute maximum is the largest $\begin{aligned} y \end{aligned}$ -value on the graph. These ideas are further illustrated in the following video:
::一种识别本地 extrema 的方法是查看图表。本地最小值是以山谷形式出现的图表上的所有 Y 值。本地最大值是作为山顶出现的图表上的所有 Y 值。绝对最小值是图上最小的 y 值。绝对值是图上最大的 y 值。这些想法在下面的视频中进一步说明 :



Global or Absolute Extrema and Local or Relative Extrema
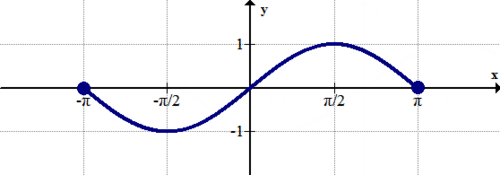
::全球或绝对Extrema和当地或相对Extrema

A global maximum point refers to the point with the largest $\begin{aligned} y \end{aligned}$ -value on the graph of a function when a largest $\begin{aligned} y \end{aligned}$ -value exists . A global minimum point refers to the point with the smallest $\begin{aligned} y \end{aligned}$ -value. Together these two values are referred to as global extrema. Global refers to the entire domain of the function . Global extrema are also called absolute extrema. There can be only one global maximum value and only one global minimum value. For example, $\begin{aligned} f (x) = \sin x \end{aligned}$ has infinitely many global maximum points and global minimum points, but only one global maximum value and only one global minimum value.
::当存在最大 Y 值时,全球最大点指函数图中最大 y 值的点。全球最低点指最小 y 值的点。这两个值加起来称为全球 extrema。 Global 指该函数的整个领域。 Global extrema 也称为绝对 extrema。只有一个全球最大值, 只有一个全球最低值。例如, f(x) = sinx 拥有无限多的全球最大值和全球最低点, 但只有一个全球最大值, 只有一个全球最低值。

In addition to global maximums and global minimums, there are also local extrema or relative maximums and relative minimums. The word "relative" is used because, in relation to some neighborhood, these values stand out as being the highest or the lowest. The graph of the function below is defined for a closed interval and illustrates the global maximum, global minimum, local maximum, and local minimum values.
::除了全球最大值和全球最低值之外,还存在局部极端值或相对最高值和相对最低值。使用“相对”一词是因为相对于某些邻里,这些值是最高值或最低值。下面的函数图为封闭间隔而定义,并显示全球最高值、全球最低值、地方最高值和当地最低值。

Locating these values is one goal of calculus. In this course, extreme values will be determined by inspection or using technology.
::确定这些值是微积分的一个目标,在这一过程中,极端值将通过检查或使用技术来确定。

Examples
::实例

Example 1
::例1

Identify and categorize all extrema:
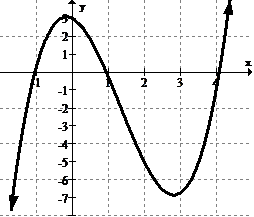
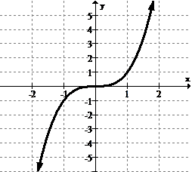
::识别并分类所有 extrema :

Solution:
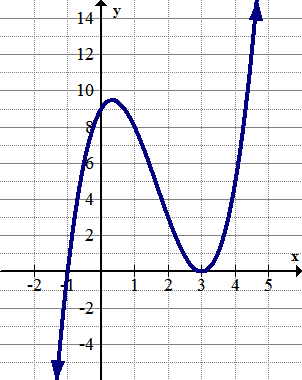
::解决方案 :

Since the function increases and decreases without bound , there are no global extrema. There is a local maximum point at approximately (-0.25, 3) and a local minimum point at approximately (2.8, -7).
::由于功能的增减没有约束,因此没有全球极限值,在大约(-0.25, 3)和大约(2.8, - 7)的地方最低点上都有一个地方最高点。

Example 2
::例2

Identify and categorize all extrema for the given function defined on the closed interval:
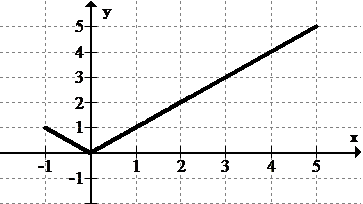
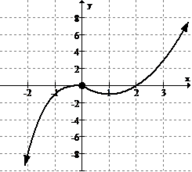
::识别并分类封闭间隔上定义的给定函数的所有 extrema :

Solution:
::解决方案 :

T he endpoints of the graph of the function are important. The $\begin{aligned} y \end{aligned}$ -values from these points are included in the set of possible extreme values.
::函数的图形端点很重要。这些端点的y值包含在一套可能的极端值中。

There is a global minimum point and a local minimum point at (0, 0). The global maximum point is located at the endpoint (5, 5), and there is no local maximum point.
::有全球最低点和当地最低点(0,0),全球最高点位于终点(5,5),没有当地最高点。

Example 3
::例3

Identify and categorize all extrema:
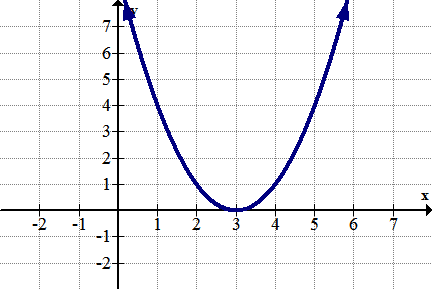
::识别并分类所有 extrema :

Solution:
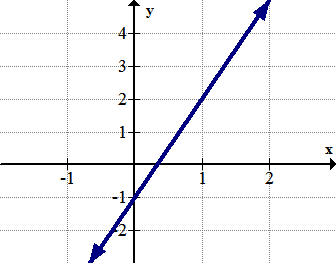
::解决方案 :

Since this function increases to $\begin{aligned} \infty \end{aligned}$ as $\begin{aligned} x \end{aligned}$ increases, there is no global maximum and no local maximum. At the only endpoint, there is a global minimum value of 0 .
::由于此函数随着 x 的增加而增加至 ,因此没有全球最大值和本地最高值。在唯一的终点,全球最低值为 0 。

Example 4
::例4

Identify and categorize all extrema:
::识别并分类所有 extrema :

Solution:
::解决方案 :

There are no global or local maximums or minimums. The function flattens near $\begin{aligned} x = 0 \end{aligned}$ , but does not have a minimum or maximum value.
::没有全球或本地的上限或最小值。函数平板接近 x=0, 但没有最小值或最大值。

Example 5
::例5

Identify and categorize the extrema:
::辨别和分类 extrema :

Solution:
::解决方案 :

There are no global extrema. There appears to be a local maximum point at (0, 0) and a local minimum point at (1, -1).
::没有全球极限值。似乎有当地最高点( 0, 0) 和当地最低点(1, 1) (1, 1) 。

Example 6
::例6

Identify and categorize the extrema:
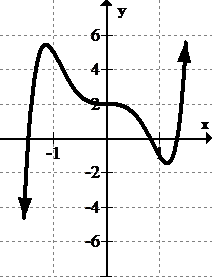
::辨别和分类 extrema :

Solution:
::解决方案 :

There are no global extrema. There appears to be a local maximum point at (-1.2, 5.3) and a local minimum point at (1.2, -1.8). Note that these values are approximated.
::没有全球极限值,在(1.2,5.3)和(1.2,1.8)地方最低点值上似乎都有一个地方最高点。注意这些值是近似值。

Summary
::摘要

Maximum and minimum points identify the highest points and the lowest points, or the peaks and the valleys, in a graph.
::在图表中,最大和最低点表示最高点和最低点,或峰值和山谷。

The absolute extreme values are the highest or lowest function values across the entire domain of the function .
::绝对极端值是函数整个领域的最高或最低函数值。

The relative extreme values are the highest or lowest function values within an interval.
::相对极端值是间隔内最高或最低函数值。

Review
::回顾

Use the graph below for 1-2:
::1-2使用下图:

1. Identify any global extrema.
::1. 查明任何全球极端。

2. Identify any local extrema.
::2. 标明任何局部端口。

Use the graph below for 3-4:
::3-4使用下图:

3. Identify any global extrema.
::3. 查明任何全球极端。

4. Identify any local extrema.
::4. 标明任何局部端口。

Use the graph below for 5-6:
::5-6 使用下图 :

5. Identify any global extrema.
::5. 查明任何全球极端。

6. Identify any local extrema.
::6. 标明任何局部端口。

Use the graph below for 7-8:
::7-8 使用下图 :

7. Identify any global extrema.
::7. 查明任何全球极端。

8. Identify any local extrema.
::8. 标明任何局部端口。

Use the graph below for 9-10:
::9-10使用下图:

9. Identify any global extrema.
::9. 查明任何全球极端。

10. Identify any local extrema.
::10. 查明任何局部端口。

11. Explain the difference between a global maximum and a local maximum.
::11. 解释全球最高比率与地方最高比率之间的差别。

12. Draw an example of a graph with a global minimum and a local maximum, but no global maximum.
::12. 绘制一个具有全球最低值和当地最高值但无全球最高值的图表的例子。

13. Draw an example of a graph with local maximums and minimums, but no global extrema.
::13. 绘制一个带有本地最大值和最小值但无全球外形的图形示例。

14. Use a graphing device t o identify and categorize the extrema of
::14. 使用图形设备来识别和分类

       $\begin{aligned} f (x) = \frac{1}{2} x^{4} + 2 x^{3} - 6.5 x^{2} - 20 x + 24. \end{aligned}$
::f(x) = 12x4+2x3- 6.5x2-20x+24。

15. Use a graphing device to identify and categorize the extrema of
::15. 使用图形设备来识别和分类

      $\begin{aligned} g (x) = - x^{4} + 2 x^{3} + 4 x^{2} - 2 x - 3. \end{aligned}$
::g(x)x4+2x3+4x2-2x-3。

16. A rectangle has area 20 in 2 . Write an expression for the perimeter of the rectangle as a function of its width, $\begin{aligned} x \end{aligned}$ . What dimensions of the rectangle will minimize its perimeter? What is the minimum perimeter?
::16. 矩形的面积为 20 英寸 2 。矩形的外形以其宽度的函数表示矩形的周边。矩形的哪一维将最大限度地缩小其周界? 最小的周界是什么?

17. A rectangle has perimeter $\begin{aligned} P \end{aligned}$ . Write a function for the area of the rectangle as a function of $\begin{aligned} P \end{aligned}$ and $\begin{aligned} x \end{aligned}$ , the width of the rectangle. What do you think will be the rectangle with maximum area?
::17. 矩形有一个矩形周边P. 写入矩形区域的函数,作为矩形宽度的P和x的函数。你认为什么是最大区域的矩形?

18. A rectangular lot beside a river is fenced on the other 3 sides with 80 feet of fencing. What is the largest possible size of the lot?
::18. 河流旁的长方形地块在另外三边围有80英尺栅栏的栅栏,该地块的最大面积是多少?

Review (Answers )
::回顾(答复)

Please see the Appendix.
::请参看附录。

最大和最低

Section outline

Introduction
::导言

Local and Absolute Maximum and Minimum
::本地和绝对最大和最低

Global or Absolute Extrema and Local or Relative Extrema
::全球或绝对Extrema和当地或相对Extrema

Examples
::实例

Summary
::摘要

Review
::回顾

Review (Answers )
::回顾(答复)

Section outline

Introduction ::导言

Local and Absolute Maximum and Minimum ::本地和绝对最大和最低

Global or Absolute Extrema and Local or Relative Extrema ::全球或绝对Extrema和当地或相对Extrema

Examples ::实例

Summary ::摘要

Review ::回顾

Review (Answers ) ::回顾(答复)

Introduction
::导言

Local and Absolute Maximum and Minimum
::本地和绝对最大和最低

Global or Absolute Extrema and Local or Relative Extrema
::全球或绝对Extrema和当地或相对Extrema

Examples
::实例

Summary
::摘要

Review
::回顾

Review (Answers )
::回顾(答复)