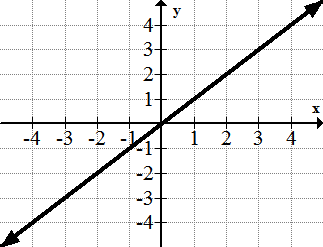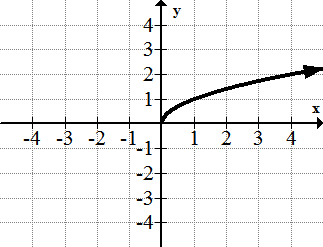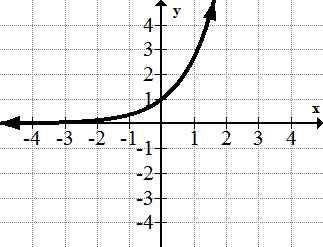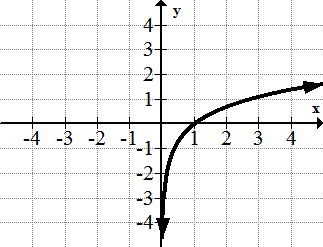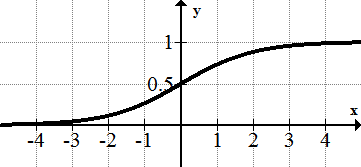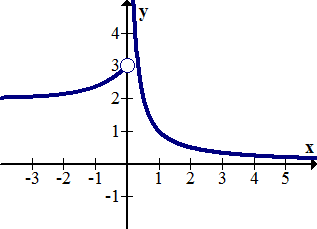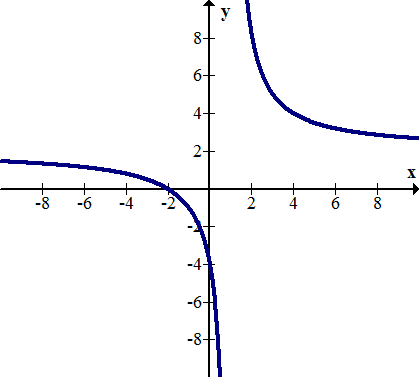节: 零星和结束行为 | 2.10 单生物和结束行为

章节大纲

Introduction
::导言

To understand the behavior of a function, it is helpful to view its graph. When a graph is displayed, typically the portion near the origin is visible. But there are times when an analyst needs to determine the behavior of the graph outside this region. To show this long- term behavior within a narrow viewing area, several techniques have been developed. In this section, you will study these techniques in order to determine the long-term behavior of a function.
::要理解函数的行为, 查看它的图形是有用的。当显示一个图形时, 通常会看到接近源头的部分。但有时分析师需要确定此区域外的图形行为。要在狭小的查看区显示这种长期行为, 已经开发了几种技术。在本节中, 您将研究这些技术, 以便确定函数的长期行为。

Consider this example: A law enforcement agency gathered data about the number of crime incidents per year in a specific region. The number of crime incidents can be modeled using the given function, where $\begin{aligned} t \end{aligned}$ represents the time since 2005:
::考虑这个例子:执法机构收集了特定区域每年犯罪事件数量的数据,犯罪事件数量可使用特定功能作为模型,其中t表示2005年以来的时间:

$\begin{aligned} N (t) = 3, 500 (\frac{1}{1 + 1.025 e^{- 0.6 t}}) \end{aligned}$

:t)=3,500(11+1.025e-0.6t)

The graph of this function will allow law enforcement to understand long-term behavior and predict the number of crimes in the future. Notice that as the year approaches 2015, the number of crimes in this region seems to be approaching 3, 500 crimes per year in the area, but will not exceed that number. This means the function is approaching $\begin{aligned} y = 3, 500 \end{aligned}$ asymptotically, and the horizontal line is the function's horizontal asymptote.
::这一功能的图解将使执法部门能够理解长期行为并预测未来犯罪的数量。请注意,随着2015年的临近,该地区每年的犯罪数量似乎接近3,500起,但不会超过这一数量。这意味着该功能正在逐渐接近y=3,500, 水平线是该函数的横向零点。

End Behavior of Polynomials
::终止多配偶行为

The end behavior of a function describes the long-term behavior of a function as $\begin{aligned} x \end{aligned}$ approaches negative infinity or positive infinity. When the function is a polynomial, then the end behavior can be determined by considering the sign on the leading coefficient and whether the degree of the function is odd or even.
::函数的结束行为描述函数的长期行为为 x 接近负无限或正无限。当函数是多数值时, 最终行为可以通过考虑主要系数的符号以及函数的大小是否奇特来决定。

When the degree of the polynomial is even and the leading coefficient is positive, then the function approaches positive infinity as $\begin{aligned} x \end{aligned}$ approaches negative infinity and positive infinity.
::当多元系数是偶数,而主要系数是正数时,当函数接近正无穷时,x接近负无穷和正无穷。

When the degree of the polynomial is even and the leading coefficient is nega tive, then the function approaches negative infinity as $\begin{aligned} x \end{aligned}$ approaches negative infinity and positive infinity.
::当多元系数的幅度相等而主要系数为负值时,当函数接近负无限度时,当x接近负无限度和正无限度时,该函数接近负无限度。

When the degree of the polynomial is odd and the leading coefficient is positive, then the function approaches positive infinity as $\begin{aligned} x \end{aligned}$ approaches positive infinity, and the f unction approaches negative infinity as $\begin{aligned} x \end{aligned}$ approaches negative infinity .
::当多数值度是奇数,而主要系数是正数时,当函数接近正无穷时,当函数接近正无穷时,当函数接近正无穷时,当函数接近负无穷时,当函数接近负无穷时,当函数接近负无穷时,当函数接近负无穷时。

When the degree of the polynomial is odd and the leading coefficient is negative, then the function approaches negati ve infinity as $\begin{aligned} x \end{aligned}$ approaches positive infinity, and the f unction approaches positive infinity as $\begin{aligned} x \end{aligned}$ approaches negative infinity .
::当多数值度是奇数,而主要系数是负数时,当函数接近负无穷时,当函数接近负无穷时,x接近正无穷,而函数接近正无穷时,x接近负无穷时,函数接近正无穷。

Asymptotes
::单生数

A vertical asymptote is a vertical line, such as $\begin{aligned} x = 1 \end{aligned}$ , marking a specific value toward which the graph of a function may approach but will never reach .
::垂直无线是一个垂直线,如 x=1, 标记函数的图形可能接近但永远无法达到的特定值。

A horizontal asymptote is a horizontal line such as $\begin{aligned} y = 4 \end{aligned}$ . It indicates a range value that the function approaches as $\begin{aligned} x \end{aligned}$ approaches positive infinity or negative infinity. A function may touch or pass through a horizontal asymptote.
::水平无线线是一个水平线, 如 y= 4 。它表示一个范围值, 函数以 x 接近正无线或负无线的方式接近。函数可以触摸或通过水平无线。

The reciprocal function has two asymptotes, one vertical and one horizontal.
::互惠功能有两个小数点,一个是垂直的,一个是横向的。

Play, Learn and Explore Asymptotes and End Behavior:
::玩耍、学习和探索小事件和结束行为:

Examples
::实例

Example 1
::例1

Identify the horizontal asymptote for the following function:
::识别以下函数的水平时点 :

Solution: The graph appears to flatten as $\begin{aligned} x \end{aligned}$ approaches positive infinity. The horizontal asymptote is $\begin{aligned} y = 0 \end{aligned}$ , even though the function clearly passes through this line an infinite number of times.
::解析度 : 图形似乎随着 x 接近正无穷度而平滑。水平无穷为 y=0, 即使函数明显通过这条线, 次数无限。

Example 2
::例2

Identify the asymptotes and end behavior of the following function:
::识别下列函数的小数点和末数行为 :

Solution: The function has a horizontal asymptote $\begin{aligned} y = 2 \end{aligned}$ as $\begin{aligned} x \end{aligned}$ approaches negative infinity. There is a vertical asymptote at $\begin{aligned} x = 0 \end{aligned}$ .
::解析度 : 该函数的 X 接近负无限度时, 具有水平同量 y= 2 。 x=0 时, 存在垂直同量。

Example 3
::例3

Identify the asymptotes and end behavior of the following function:
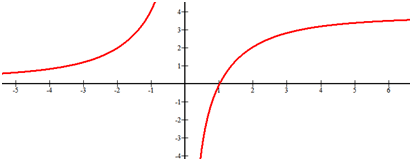
::识别下列函数的小数点和末数行为 :

Solution: There is a vertical asymptote, $\begin{aligned} x = 0 \end{aligned}$ . The horizontal asymptote as $\begin{aligned} x \end{aligned}$ approaches negative infinity is $\begin{aligned} y = 0 \end{aligned}$ and the horizontal asymptote as $\begin{aligned} x \end{aligned}$ approaches positive infinity is $\begin{aligned} y = 4. \end{aligned}$
::解析度 : 有一个垂直的无线点, x=0。水平的无线点是 y=0, 水平的无线点是 y=4, 水平的无线点是 x 的正无线点是 y=4 。

Example 4
::例4

Identify the horizontal and vertical asymptotes of the following function:
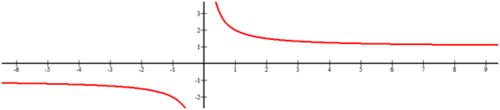
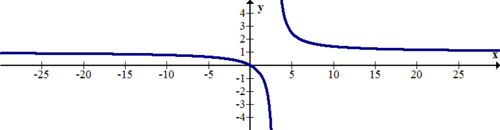
::识别以下函数的水平和垂直单位数:

Solution: There is a vertical asymptote, $\begin{aligned} x = 0 \end{aligned}$ . As $\begin{aligned} x \end{aligned}$ approaches negative infinity , there is a horizontal asymptote, $\begin{aligned} y = - 1 \end{aligned}$ . As $\begin{aligned} x \end{aligned}$ approaches positive infinity , there is another horizontal asymptote, $\begin{aligned} y = 1 \end{aligned}$ .
::解答 : 存在垂直无线, x=0。 x 接近负无线时, 存在水平无线, y1. x 接近正无线, 还有另一个水平无线, y=1 。

Example 5
::例5

Identify the horizontal and vertical asymptotes of the following function:
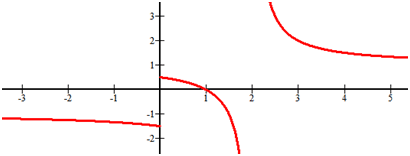
::识别以下函数的水平和垂直单位数:

Solution: There is a vertical asymptote, $\begin{aligned} x = 2 \end{aligned}$ . At $\begin{aligned} x = 0 \end{aligned}$ , there is a break in the graph but not a vertical asymptote. As $\begin{aligned} x \end{aligned}$ approaches negative infinity , there is a horizontal asymptote, $\begin{aligned} y = - 1 \end{aligned}$ . As $\begin{aligned} x \end{aligned}$ approaches positive infinity , there is another horizontal asymptote, $\begin{aligned} y = 1 \end{aligned}$ .

::解析度 : 存在垂直静态, x=2 。在 x=0 时, 图形有一个断裂, 但不是垂直静态。 x 接近负无穷时, 存在水平静态, y 。 x 接近正无穷时, y= 1 。当 x 接近正无穷时, 还有一个水平静态, y= 1 。

Example 6
::例6

Identify the horizontal and vertical asymptotes based on the graph of the following piecewise function:
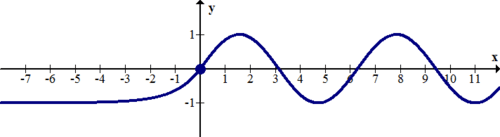
::根据以下按片段函数的图形, 识别水平和垂直的单位数 :

$\begin{aligned} f (x) = {\begin{cases} e^{x} - 1 & x \leq 0 \\ \sin x & 0 < x \end{cases} \end{aligned}$
:x)\\\ ex- 1x0sin\\ x0 <x)

Solution: There is a horizontal asymptote, $\begin{aligned} y = - 1 \end{aligned}$ , as $\begin{aligned} x \end{aligned}$ approaches negative infinity.
::解答: 存在一个水平的零星, y1, x 接近负无穷。

Summary
::摘要

The end behavior of a function describes the long-term behavior of a function as $\begin{aligned} x \end{aligned}$ approaches negative infinity and positive infinity.
::函数的结束行为描述函数的长期行为为 x 接近负无限和正无限。

A vertical asymptote is a vertical line that marks a specific value toward which the graph of a function may approach but will never reach .
::垂直线是一个垂直线条,该线条代表一个函数的图形可能接近但永远不会达到的具体值。

A horizontal asymptote is a horizontal line that the graph of a function approaches as $\begin{aligned} x \end{aligned}$ approaches positive infinity or negative infinity.
::水平无线线是一个水平线, 函数的图形以 x 接近正无线或负无线为方向。

Graphing asymptotes is a method to illustrate the long-term behavior of a function. They are usually identified with dotted lines on the graph of the function, and indicate how the function will behave outside the viewing window.
::绘制 asymptotes 是用来说明函数的长期行为的一种方法。它们通常在函数图中用虚线识别, 并显示函数在查看窗口外的行为方式。

Review
::回顾

Identify the asymptotes and end behavior of the following functions:
::识别下列函数的小数点和末数行为 :

1. $\begin{aligned} y = x \end{aligned}$
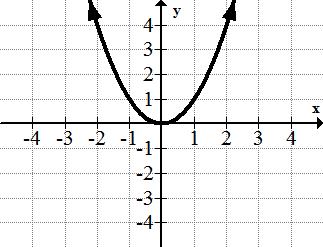
::1.y=x

2. $\begin{aligned} y = x^{2} \end{aligned}$
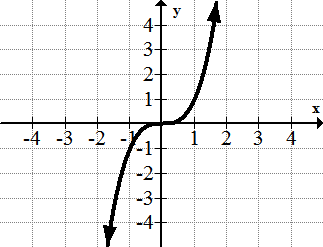
::2. y=x2

3. $\begin{aligned} y = x^{3} \end{aligned}$
::3. y=x3

4. $\begin{aligned} y = \sqrt{x} \end{aligned}$
::4.y=x

5. $\begin{aligned} y = \frac{1}{x} \end{aligned}$
::5. y=1x

6. $\begin{aligned} y = e^{x} \end{aligned}$
::6. y=ex

7. $\begin{aligned} y = \ln (x) \end{aligned}$
::7.y=ln(x)

8. $\begin{aligned} y = \frac{1}{1 + e^{- x}} \end{aligned}$
::8. y=11+e-x

9.

10.

11.

12. Explain why it makes sense that $\begin{aligned} y = \frac{1}{x} \end{aligned}$ has a vertical asymptote at $\begin{aligned} x = 0 \end{aligned}$ .
::12. 解释为什么y=1x在 x=0 时有一个垂直的空位是有道理的。

13. Explain why it makes sense that $\begin{aligned} y = \frac{1}{x + 3} \end{aligned}$ has a vertical asymptote at $\begin{aligned} x = - 3 \end{aligned}$ .
::13. 解释为什么y=1x+3在 x3 上有一个垂直的静态,这是有道理的。

14. Use the technique from the previous problem to determine the vertical asymptote for the function $\begin{aligned} y = \frac{1}{x - 2} \end{aligned}$ .
::14. 使用上一个问题的技术来确定函数y=1x-2的垂直静态。

15. Use the technique from problem #13 to determine the vertical asymptote for the function $\begin{aligned} y = \frac{2}{x + 4} \end{aligned}$ .
::15. 使用问题13的技术确定函数y=2x+4的垂直空点。

Review (Answers )
::回顾(答复)

Please see the Appendix.
::请参看附录。

零星和结束行为

章节大纲

Introduction
::导言

End Behavior of Polynomials
::终止多配偶行为

Asymptotes
::单生数

Examples
::实例

Summary
::摘要

Review
::回顾

Review (Answers )
::回顾(答复)

章节大纲

Introduction ::导言

End Behavior of Polynomials ::终止多配偶行为

Asymptotes ::单生数

Examples ::实例

Summary ::摘要

Review ::回顾

Review (Answers ) ::回顾(答复)

Introduction
::导言

End Behavior of Polynomials
::终止多配偶行为

Asymptotes
::单生数

Examples
::实例

Summary
::摘要

Review
::回顾

Review (Answers )
::回顾(答复)