节: 实际多党零分数 | 3.5 实际复数为零

章节大纲

Introduction
::导言

Unlike those often found in textbooks , problems in real life do not always fit easily into quadratic or even cubic equations. Financial models, population models, fluid activity, etc., often require of higher degree in order to approximate the overall behavior. Although it is challenging to model some of these more complex interactions, the effort can be well worth it. Mathematical models of stocks are used constantly to "look into the future" and make the kinds of educated guesses that create safe and stable investment portfolios .

To graph more complicated polynomial functions, we need powerful methods to find the zeros . Synthetic division can verify the zeros, but knowing where they are located is often a mystery. Several theorems summarize these methods:
::要绘制更复杂的多元函数图,我们需要强大的方法来找到零。合成分裂可以验证零,但知道它们的位置往往是一个谜。一些理论总结了这些方法:

Remainder Theorem
::保留定理

Factor Theorem
::因数定理

Rational Zero Theorem
::推理为零定理

Descartes's Rule of Sign
::笛卡尔的签署规则

These theorems and rules help make the discovery of the roots of polynomial functions easier.
::这些理论原理和规则有助于更容易发现多元功能的根源。

lesson content

The last theorem listed, credited to Rene Descartes (pictured) in his work La Géom é trie , helps us calculate the upper bound on the number of roots and their signs.
::La Géométrie作品中最后列出的归名为Rene Descartes(肖像)的理论帮助我们计算根数及其标志的上限。

The Remainder Theorem
::遗物定理

If a polynomial $\begin{aligned} f (x) \end{aligned}$ of degree $\begin{aligned} n > 0 \end{aligned}$ is divided by $\begin{aligned} x - c \end{aligned}$ , then the remainder $\begin{aligned} R \end{aligned}$ is a constant and it is equal to the value of the polynomial when $\begin{aligned} c \end{aligned}$ is substituted for $\begin{aligned} x \end{aligned}$ . That is,
::如果以x-c除以一多角 f(x) 度 n>0 除以 x > 0,那么其余的 R 是常数, 当 c 取代 x 时, 则等于多角值。也就是说,

\begin{aligned} f (c) = R . \end{aligned}

c) =R.

The Factor Theorem
::因数定理

An extension of the Remainder Theorem is the Factor Theorem. It states that if $\begin{aligned} f (x) \end{aligned}$ is a polynomial of degree $\begin{aligned} n > 0 \end{aligned}$ and $\begin{aligned} f (c) = 0 \end{aligned}$ , then $\begin{aligned} x - c \end{aligned}$ is a factor of the polynomial $\begin{aligned} f (x) \end{aligned}$ . Conversely , if $\begin{aligned} x - c \end{aligned}$ is a factor, then $\begin{aligned} c \end{aligned}$ is a zero of $\begin{aligned} f . \end{aligned}$
::保存者定理的延伸是因子定理。它指出, 如果 f(x) 是一度为n>0和 f(c)=0, 那么 x- c 是多度为 f(x) 的一个因数。相反, 如果 x- c 是一因数, 那么c 是 f 0 。

The Rational Zero Theorem
::理性的零定理

Given the polynomial
::以多面体为背景

\begin{aligned} f (x) = a_{n} x^{n} + a_{n - 1} x^{n - 1} + \dots + a_{1} x + a_{0}, \end{aligned}

x) = anxn+an- 1xn- 1a1x+a0,

$\begin{aligned} a_{n} \neq 0 \end{aligned}$ and $\begin{aligned} n \end{aligned}$ is a positive integer . If the coefficients are integers and $\begin{aligned} \frac{p}{q} \end{aligned}$ is a rational zero in lowest terms , then $\begin{aligned} p \end{aligned}$ is a divisor of $\begin{aligned} a_{0} \end{aligned}$ and $\begin{aligned} q \end{aligned}$ is a divisor of $\begin{aligned} a_{n} . \end{aligned}$
::an0和 n 是一个正整数。如果系数是整数,而pq是最低值的合理零,那么p是a0的差数,q是a的差数。

Descartes's Rule of Signs
::笛卡尔的标志规则

Given any polynomial $\begin{aligned} p (x) \end{aligned}$ , the maximum number of positive roots can be determined by this method:
::考虑到任何多面 p(x), 最大正根数可以通过此方法确定 :

Write the terms of $\begin{aligned} p (x) \end{aligned}$ in descending order (i.e., from the highest degree term to the lowest degree term).
::以降序顺序(即从最高学位到最低学位)撰写p(x)条款。

Count the number of sign changes in the sequence of terms in $\begin{aligned} p (x) \end{aligned}$ . Call the number of sign changes $\begin{aligned} r \end{aligned}$ .
::计数 p(x) 中术语序列的符号更改次数。调用 r 的符号更改次数 r 。

Note that the maximum number of positive roots of $\begin{aligned} p (x) \end{aligned}$ is less than or equal to $\begin{aligned} r \end{aligned}$ . Further, the possible number of positive roots is $\begin{aligned} r, r - 2, r - 4, \dots \end{aligned}$
::注意p(x)正根的最大数量小于或等于r。此外,正根的可能数量是r,r-2,r-4,...

Similarly, given any polynomial $\begin{aligned} p (x) \end{aligned}$ , the maximum number of negative roots can be determined by this method:
::同样,如果存在任何多面p(x),通过这种方法可以确定最大负根数:

Substitute $\begin{aligned} - x \end{aligned}$ for $\begin{aligned} x \end{aligned}$ in $\begin{aligned} p (x) \end{aligned}$ so that you have $\begin{aligned} p (- x) \end{aligned}$ (i.e., change the sign of all terms in $\begin{aligned} p (x) \end{aligned}$ with odd powers).
::p( x) 中 x 的替代 - x , 这样您就可以有 p - x (即用奇数更改 p( x) 中所有术语的符号) 。

Write the terms of $\begin{aligned} p (- x) \end{aligned}$ in descending order.
::按降序写p(-x)的条款。

Count the number of sign changes in the sequence of terms as above.
::计算上面术语序列中的符号更改次数。

Note that the maximum number of negative roots is less than or equal to the number of sign changes.
::注意负根的最大数量小于或等于符号更改的数量。

Finding Zeros
::查找零

When asked to find all of the zeros of a polynomial function , follow the steps as follows:
::当被要求查找多元函数的所有零时,请遵循以下步骤:

Apply the Rational Zero Theorem by listing all of the possible rational zeros by dividing each of the factors of the constant term by the factors of the leading coefficient .
::应用理性的零理论,列出所有可能的理性零点,用主要系数的系数将常值的每个系数除以。

Apply Descartes's Rule of Signs to determine the number of possible positive and negative real zeros.
::应用笛卡尔的标志规则确定可能的正数和负数实际零数

Use the Factor Theorem or synthetic division to determine if any of the possible rational zeros are actual zeros.
::使用系数定理或合成分解来确定任何可能的理性零是实际零。

F ind all of the zeros by dividing the polynomial by the binomial factor found using the Factor Theorem or synthetic division.
::通过将多数值除以使用因子定理或合成分解发现的二数系数来查找所有零。

Examples
::实例

Example 1
::例1

Use synthetic division and the Remainder and Factor theorems to find the quotient $\begin{aligned} Q (x) \end{aligned}$ and the remainder $\begin{aligned} R \end{aligned}$ if $\begin{aligned} f (x) = 2 x^{3} - 3 x^{2} + 6 \end{aligned}$ is divided by $\begin{aligned} x - 5 \end{aligned}$ .
::使用合成分块以及残留物和因子定理来找到商数Q(x),如果f(x)=2x3-3x2+6除以x-5,则其余R除以x-5。

Solution:
::解决方案 :

Step 1: Perform s ynthetic division :
::第1步:进行合成分解:

\begin{aligned} 5) \bar{2 - 3 0 6} \\ \underline{↓ 10 35 175} \\ 2 7 35 181. \end{aligned}

Step 2: Apply the obtained coefficients to the quotient $\begin{aligned} Q (x) \end{aligned}$ :
::第2步:将获得的系数适用于商数Q(x):

\begin{aligned} 2 x^{3} - 3 x^{2} + 6 = (2 x^{2} + 7 x + 35) (x - 5) + 181. \end{aligned}

::2x3-3x2+6=(2x2+7x+35)(x-5)+181。

Note: The remainder is 181, and it can also be obtained if we substitute $\begin{aligned} x = 5 \end{aligned}$ into $\begin{aligned} f (x) \end{aligned}$ :
::注:其余为181,如果我们将x=5改为f(x),也可以获得:

\begin{aligned} f (5) & = 2 (5)^{3} - 3 (5)^{2} + 6 \\ = 250 - 75 + 6 \\ = 181. \end{aligned}

::f(5)=2(5)3-3(5)2+6=250-75+6=181。

Example 2
::例2

Use the Rational Zero Theorem and synthetic division to find all the possible rational zeros of the polynomial
::使用理性零定理和合成分解来查找多元论的所有可能的理性零

\begin{aligned} f (x) = x^{3} - 2 x^{2} - x + 2. \end{aligned}

x) =x3-2x2-x2+2。

Solution:
::解决方案 :

Step 1: The Rational Zero Theorem states if $\begin{aligned} \frac{p}{q} \end{aligned}$ is a rational root , then $\begin{aligned} p \end{aligned}$ is a divisor of the constant term of the polynomial $\begin{aligned} f (x) \end{aligned}$ and $\begin{aligned} q \end{aligned}$ is a divisor of its leading coefficient. So $\begin{aligned} p \end{aligned}$ is a divisor of 2 and $\begin{aligned} q \end{aligned}$ is a divisor of 1. Hence, $\begin{aligned} p \end{aligned}$ can take the following values: -1, 1, -2, 2, and $\begin{aligned} q \end{aligned}$ can be either -1 or 1. Therefore , the possible values of $\begin{aligned} \frac{p}{q} \end{aligned}$ are
::步骤 1: 理性零理论表示 pq 是理性根, p 是常数的常数。所以 p 是 2 的 divisor, q 是 1 的 divisor。因此, p 需要以下值: - 1, 1, 1, 2, 2, q 可以是 - 1 或 1 。因此, pq 的可能值是 1 。

\begin{aligned} \frac{p}{q} : - 1, 1, - 2, 2. \end{aligned}

::pq:-1,1,2-2,2。

Step 2: T here are four possible zeros. Of these four, not more than three can be zeros of $\begin{aligned} f \end{aligned}$ because $\begin{aligned} f \end{aligned}$ is a polynomial with degree 3. To test which of the four possible candidates are zeros of $\begin{aligned} f \end{aligned}$ , we use synthetic division.
::第2步:可能为4个零。在这4个零中,最多不超过3个是f的零,因为f是具有第3级的多元性。为了测试4个可能的候选者中哪一个是f的零,我们使用合成分法。

Step 3: We use synthetic division to check to see if 2 is indeed a factor:
::步骤3:我们利用合成分区检查2是否确实是一个因素:

\begin{aligned} 2) \bar{1 - 2 - 1 2} \\ \underline{↓ 2 0 - 2} \\ 1 0 - 1 0. \end{aligned}

Hence, 2 is a zero of $\begin{aligned} f \end{aligned}$ . Further, by division,
::因此,2是f的零。此外,按区域分列,

\begin{aligned} f (x) & = (x - c) Q (x) + R (x) \\ = (x - 2) (x^{2} - 1) + 0. \end{aligned}

::f(x)=(x-c)Q(x)+R(x)=(x-2)(x2-1)+0。

Step 4: The remaining zeros of $\begin{aligned} f \end{aligned}$ are the zeros of $\begin{aligned} Q (x) = x^{2} - 1, \end{aligned}$ which can be factored to
::第4步:F的剩余零点为Q(x)=x2-1的零点,可乘以

\begin{aligned} Q (x) & = x^{2} - 1 \\ = (x - 1) (x + 1) . \end{aligned}

::Q(x)=x2-1=(x-1)(x+1)。

Thus, the remaining zeros are -1 and 1. The rational zeros of $\begin{aligned} f \end{aligned}$ are -1, 1, and 2.
::因此,剩下的零是-1和1. F的理性零是-1、1和2。

Example 3
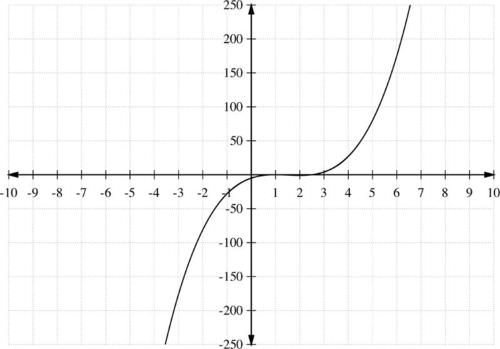
::例3

Graph the polynomial function $\begin{aligned} h (x) = 2 x^{3} - 9 x^{2} + 12 x - 5. \end{aligned}$
::图解多边函数 h( x) = 2x3- 9x2+12x-5。

Solution:
::解决方案 :

Step 1: Notice that the leading term is $\begin{aligned} 2 x^{3} \end{aligned}$ , where $\begin{aligned} n = 3 \end{aligned}$ is odd and $\begin{aligned} a_{n} = 2 > 0 \end{aligned}$ . This tells us that the end behavior will take the shape of a power function with an odd exponent . Apply the Factor Theorem and synthetic division, and we can find the rational roots of $\begin{aligned} h (x) \end{aligned}$ .
::第一步 1: 请注意, 前一学期为 2x3, 其中 n=3 是奇数, 和 an=2>0 。这告诉我们, 最终行为将使用奇数表示符数, 以功率函数的形式出现。应用因子定理和合成分解, 我们可以找到 h( x) 的合理根。

Step 2: Use the Rational Zero Theorem and find that the possible rational zeros are
::步骤2:使用理性零理论论,发现可能的理性零是

\begin{aligned} \frac{p}{q} : - 1, 1, - 2, 2, - 5, 5, - \frac{5}{2}, \frac{5}{2} . \end{aligned}

::q:-1,1,2,2,5,5,5,52,52。

Step 3: Test each number by the Factor Theorem:
::第3步:用系数定理测试每个数字:

\begin{aligned} h (- 1) = 2 (- 1)^{3} - 9 (- 1)^{2} + 12 (- 1) - 5 = - 28 \end{aligned}

::h( - 1) = 2( - 1) 3- 9( - 1) 2+12( - 1) - 528

Since the remainder is -28, -1 is not a root.
::因为剩下的是 -28, -1 不是根。

Now let's test $\begin{aligned} x = 1 \end{aligned}$ :
::现在让我们测试 x=1 :

\begin{aligned} h (1) = 2 (1)^{3} - 9 (1)^{2} + 12 (1) - 5 = 0 \end{aligned}

::h(1)=2(1)3-9(1)2+12(1)-5=0

Since the remainder is 0, 1 is a root, so use synthetic division to divide.
::由于其余为0, 1 是根, 所以使用合成分裂来分割。

\begin{aligned} 1) \bar{2 - 9 12 - 5} \\ \underline{↓ 2 - 7 5} \\ 2 - 7 5 0. \end{aligned}

Step 4: Rewrite $\begin{aligned} h (x) \end{aligned}$ since 1 is a zero:
::第4步:重写h(x),因为1为零:

\begin{aligned} h (x) = (2 x^{2} - 7 x + 5) (x - 1) . \end{aligned}

::h(x) = (2x2-7x+5)(x-1) 。

Step 5: Factor the quadratic and solve for the roots:
::步骤5: 将根的二次方和溶解值乘以 :

\begin{aligned} 2 x^{2} - 7 x + 5 = (2 x - 5) (x - 1) \end{aligned}

\begin{aligned} h (x) = (2 x - 5) (x - 1)^{2} \\ 2 x - 5 = 0 or x - 1 = 0. \end{aligned}

::2x2-7x+5=(2x-5)(x-1) h(x)=(2x-5)(x-1)-222x-5=0或x-1=0)。

Thus, 1 and $\begin{aligned} \frac{5}{2} \end{aligned}$ are the $\begin{aligned} x - \end{aligned}$ intercepts of $\begin{aligned} h (x) \end{aligned}$ .
::因此,1和52是h(x)的x-拦截。

Step 6: The $\begin{aligned} y - \end{aligned}$ intercept is
::步骤6: y - 界面是

\begin{aligned} h (0) = - 5. \end{aligned}

0)5。

Further, synthetic division or the Remainder Theorem can be also used to form a table of values for the graph of $\begin{aligned} h (x) \end{aligned}$ :
::此外,合成分裂或残余定理也可以用来组成h(x)图的数值表:

\begin{aligned} x & - 1 & 0 & 1 & 2 & \frac{5}{2} & 3 \\ h (x) & - 28 & - 5 & 0 & - 1 & 0 & 4 \end{aligned}

::2523h(x)-28-50-104

Step 7: C hoose test points from each interval and find $\begin{aligned} h (x) \end{aligned}$ :
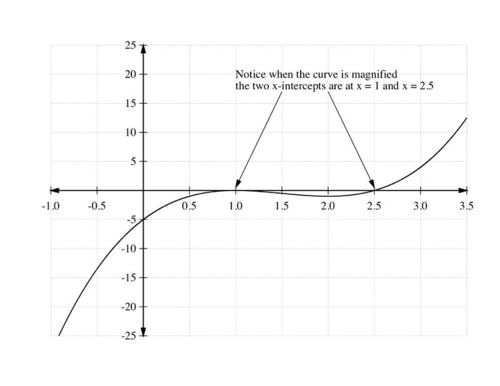
::步骤7:从每个间隔选择测试点并查找 h(x) :

Interval	Test Value $\begin{aligned} x \end{aligned}$	$\begin{aligned} h (x) \end{aligned}$	Sign of $\begin{aligned} h (x) \end{aligned}$	Location of points on the graph
$\begin{aligned} (- \infty, 1) \end{aligned}$	-1	-28	-	below the $\begin{aligned} x - \end{aligned}$ axis
$\begin{aligned} (1, \frac{5}{2}) \end{aligned}$	$\begin{aligned} \frac{3}{2} \end{aligned}$	$\begin{aligned} \frac{- 1}{2} \end{aligned}$	-	below the $\begin{aligned} x - \end{aligned}$ axis
$\begin{aligned} (\frac{5}{2}, \infty) \end{aligned}$	3	4	+	above the $\begin{aligned} x - \end{aligned}$ axis

Using this information, the graph of $\begin{aligned} h (x) \end{aligned}$ is shown in the two graphs below. Notice that the 2nd graph is a magnification of $\begin{aligned} h (x) \end{aligned}$ in the vicinity of the $\begin{aligned} x - \end{aligned}$ axis:
::使用此信息, h(x) 的图形在以下两个图表中显示。请注意, 第二图是 x- 轴附近 h(x) 的放大值 :

lesson content

Example 4
::例4

a) Show that $\begin{aligned} x + 3 \end{aligned}$ is a factor of $\begin{aligned} g (x) = x^{4} + 2 x^{3} - 3 x^{2} + 4 x + 12 \end{aligned}$ .
::a) 显示 x+3 是g(x)=x4+2x3-3x2+4x12的系数。

Solution:
::解决方案 :

By the Factor Theorem, if $\begin{aligned} f (c) = 0 \end{aligned}$ , then $\begin{aligned} x - c \end{aligned}$ is a factor of the polynomial. In other words, if synthetic division produces a remainder equal to zero, then $\begin{aligned} c \end{aligned}$ is a factor of the polynomial.
::依因数定理, 如果 f( c) =0, 那么x - c 是多元值的一个系数。换句话说, 如果合成分解产生等于零的剩余值, 那么c 是多元值的一个系数。

\begin{aligned} g (- 3) = (- 3)^{4} + 2 (- 3)^{3} - 3 (- 3)^{2} + 4 (- 3) + 12 = 0 \end{aligned}

::g(-3)=(-3)4+2(-3)3-3-3-3(-3)2+4(-3)+12=0

So, -3 is a root and $\begin{aligned} x + 3 \end{aligned}$ is a factor of $\begin{aligned} g (x) \end{aligned}$ .
::所以, -3 是根, x+3 是g(x) 的系数。

b) Find the quotient $\begin{aligned} Q (x) \end{aligned}$ and express $\begin{aligned} f (x) \end{aligned}$ in factored form .
:b) 以系数形式查找商数Q(x)和Express f(x)。

Solution:
::解决方案 :

Use synthetic division with $\begin{aligned} c = - 3 : \end{aligned}$

\begin{aligned} - 3) \bar{1 2 - 3 4 12} \\ \underline{↓ - 3 3 0 - 12} \\ 1 - 1 0 4 0. \end{aligned}

::使用与 c3:-3)1 2-3 4 12 Q3 3 0-12_1-1 0 4 0的合成分形。

Since $\begin{aligned} g (- 3) = 0 \end{aligned}$ and the quotient is $\begin{aligned} Q (x) = x^{3} - x^{2} + 4 \end{aligned}$ , $\begin{aligned} g (x) \end{aligned}$ can be written as
::由于 g( - 3) =0, 商数为 Q( x) =x3 -x2+4, g( x) 可以以下列方式写入 :

\begin{aligned} g (x) & = (x - (- 3)) (x^{3} - x^{2} + 4) \\ g (x) & = (x + 3) (x^{3} - x^{2} + 4) . \end{aligned}

Example 5
::例5

Use the Rational Zero Theorem to find all the rational zeros of the polynomial
::使用理性的零点定理来查找多元数的所有理性零

\begin{aligned} f (x) = x^{3} - 2 x^{2} - 5 x + 6. \end{aligned}

x) =x3-2x2-5x+6。

Solution:
::解决方案 :

Step 1: Assume $\begin{aligned} \frac{p}{q} \end{aligned}$ is a rational zero of $\begin{aligned} f \end{aligned}$ . By the Rational Zero Theorem, $\begin{aligned} p \end{aligned}$ is a divisor of 6 and $\begin{aligned} q \end{aligned}$ is a divisor of 1. Thus, $\begin{aligned} p \end{aligned}$ and $\begin{aligned} q \end{aligned}$ can assume the following respective values:

\begin{aligned} p : 1, - 1, 2, - 2, 3, - 3, 6, - 6 \end{aligned}

and

\begin{aligned} q : - 1, 1. \end{aligned}

Therefore, the possible rational zeros will be

\begin{aligned} \frac{p}{q} : - 1, 1, - 2, 2, - 3, 3, - 6, 6. \end{aligned}

::第1步:假设pq是f的理性零。根据理性的零理论,p是6之差,q是1之差,因此,p和q可以假定相应的数值如下:p:1:1-2,2-2,3,3,6,6和q:-1,1.因此,可能的理性零将是pq:1,1,2,2,3,3,6。

Notice that with these choices for $\begin{aligned} p \end{aligned}$ and $\begin{aligned} q, \end{aligned}$ there could be $\begin{aligned} 8 \cdot 2 = 16 \end{aligned}$ rational zeros. But 8 of them are duplicates. For example, $\begin{aligned} \frac{1}{- 1} = \frac{- 1}{1} = - 1 \end{aligned}$ .
::请注意, p 和 q 有这些选择, 可能有 82= 16 理性零。但其中 8 是重复的。例如, 1 - 1\\\\\\\\ 11\\ 1 。

Step 2: Test all these values by synthetic division (do this on your own for practice), and we finally find that $\begin{aligned} 1, - 2, and 3 \end{aligned}$ are zeros of $\begin{aligned} f \end{aligned}$ . That is,
::第2步:用合成组分来测试所有这些数值(为实践而自行测试),我们最终发现1-2和3是f的零。也就是说,

\begin{aligned} f (x) & = x^{3} - 2 x^{2} - 5 x + 6 \\ = (x - 1) (x + 2) (x - 3) . \end{aligned}

Example 6
::例6

Use Descartes's Rule of Signs to identify the maximum number of possible positive and negative roots for the function
::使用笛卡尔的标志规则确定函数的最大可能的正根和负根数

\begin{aligned} f (x) = - 2 x^{3} + x^{2} - 3 x^{5} + 5 x - 1. \end{aligned}

Solution:
::解决方案 :

Step 1: R ewrite $\begin{aligned} f (x) \end{aligned}$ in descending order:

\begin{aligned} f (x) = - 3 x^{5} - 2 x^{3} + x^{2} + 5 x - 1. \end{aligned}

::第1步:按降序重写 f(x) : f(x)\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\

The number of sign changes of $\begin{aligned} f (x) \end{aligned}$ is 2, so the number of positive roots is either 2 or 0.
::f( x) 的符号更改数为 2, 正根数为 2 或 0 。

Step 2: For the negative roots, write

\begin{aligned} f (- x) = - 3 (- x)^{5} - 2 (- x)^{3} + (- x)^{2} + 5 (- x) - 1 \\ f (- x) = 3 x^{5} + 2 x^{3} + x^{2} - 5 x - 1. \end{aligned}

::第2步:对于负根,写 f(-x)3x3(-x)5-2(-x)3+(-x)2+5(-x)2+1f(-x)=3x5+2x3+x2-2-5x-1。

Step 3: The number of sign changes of $\begin{aligned} f (- x) \end{aligned}$ is 1, so the maximum number of negative roots is 1.
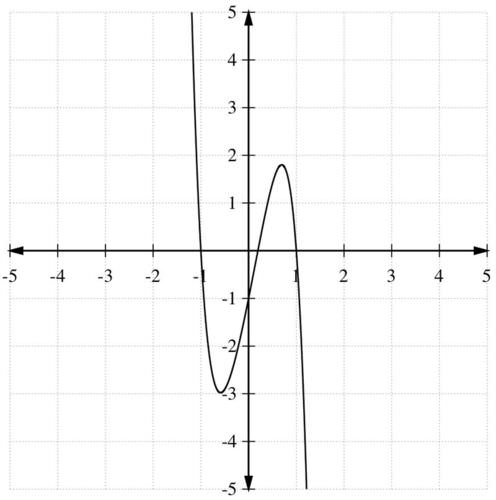
::第3步:f(-x)的标记更改数目为1,因此负根的最大数目为1。

Step 4: The graph of $\begin{aligned} f (x) \end{aligned}$ below shows that there is one negative root and two positive roots:
::第4步:f(x)下图显示有一个负根和两个正根:

lesson content

Example 7
::例7

Find the root(s) of $\begin{aligned} f (x) = 4 x^{2} - 3 x - 7. \end{aligned}$
::查找 f( x) = 4x2 - 3x- 7 的根根。

Solution:
::解决方案 :

Fact or and apply the zero product rule :
::适用 " 零产品 " 规则的因数:

\begin{aligned} 4 x^{2} - 3 x - 7 = 0 \end{aligned}

\begin{aligned} (4 x - 7) (x + 1) = 0 \end{aligned}

\begin{aligned} 4 x - 7 = 0 \end{aligned}

\begin{aligned} x + 1 = 0 \end{aligned}

\begin{aligned} x = \frac{7}{4} \end{aligned}

\begin{aligned} x = - 1 \end{aligned}

(each zero has a multiplicity of one).

Example 8
::例8

Find the real root(s) of $\begin{aligned} f (x) = x^{4} + 1 \end{aligned}$ .
::查找 f( x) =x4+1 的真实根根。

Solution:
::解决方案 :

Since there are no even roots of negative numbers, this function has no real zeros:

\begin{aligned} x^{4} & = - 1 \\ x & = \sqrt[4]{- 1} . \end{aligned}

::由于没有负数的根数,此函数没有实际零数: x41x14。

Summary
::摘要

Three theorems work together to identify and verify zeros of a polynomial:
- Remainder Theorem, which is used to quickly evaluate a polynomial;
  ::保留理论,用于快速评估多面性;
- Factor Theorem, which relates a zero remainder to a factor of a polynomial;
  ::系数定理,它将零余数与多元系数的一个系数相联系;
- Rational Zero Theorem, which creates a list of possible rational zeros.
  ::理性的零理论, 创造了一个可能的理性零的列表。
::三个论者共同确定和核实多元论的零:用于快速评估多元论的 " 保留论者理论 " ; 系数论者,将零余数与多元论系数联系起来; 逻辑论,将可能的合理零数列成一个清单。

Descartes's Rule of Sign lists possible numbers of positive and negative zeros, which helps to narrow possibilities.
::笛卡尔的《签名规则》列出了可能的正数和负数零数,这有助于缩小可能性。

Review
::回顾

Find all the possible rational solutions for the following polynomials. Use the Rational Zero Theorem:
::为以下多边协议寻找所有可能的理性解决方案。使用理性的零理论 :

$\begin{aligned} f (x) = x^{3} + 6 x^{2} - 18 x + 20 \end{aligned}$
:x) =x3+6x2-18x+20

$\begin{aligned} f (x) = 4 x^{4} + x^{2} - 15 \end{aligned}$
:xx)=4x4+x2-15)

$\begin{aligned} f (x) = - 2 x^{3} + 7 x^{2} - x + 8 \end{aligned}$
:x) f=2x3+7x2 -x+8

$\begin{aligned} f (x) = x^{4} - 3 x^{3} - 4 x^{2} + 15 x + 9 \end{aligned}$
:x) =x4- 3x3- 4x2+15x+9

$\begin{aligned} f (x) = 8 x^{4} - 5 x^{3} + 16 x^{2} + 37 x - 24 \end{aligned}$
:x) = 8x4 - 5x3+ 16x2+ 37x- 24

Find all the real-number solutions for each function below. Use any method you like:
::查找以下每个函数的所有真实数字解决方案。使用您喜欢的任何方法 :

$\begin{aligned} f (x) = 6 x^{3} - 17 x^{2} + 11 x - 2 \end{aligned}$
:x)=6x3-17x2+11x-2

$\begin{aligned} f (x) = x^{4} + 7 x^{3} + 6 x^{2} - 32 x - 32 \end{aligned}$
:x) =x4+7x3+6x2 - 32x-32

$\begin{aligned} f (x) = 16 x^{3} + 40 x^{2} - 25 x - 3 \end{aligned}$
:x) = 16x3+40x2- 25x-3

$\begin{aligned} f (x) = 2 x^{3} - 9 x^{2} + 21 x - 18 \end{aligned}$
:x) = 2x3- 9x2+21x- 18

$\begin{aligned} f (x) = 4 x^{3} - 16 x^{2} + 39 x - 295 \end{aligned}$
:x)=4x3-16x2+39x-295

$\begin{aligned} f (x) = 6 x^{4} + x^{3} - 29 x^{2} + 17 x + 5 \end{aligned}$
::f(x)=6x4+x3-29x2+17x+5

$\begin{aligned} f (x) = x^{5} + 7 x^{4} - 3 x^{3} - 65 x^{2} - 8 x + 156 \end{aligned}$
::f(x) =x5+7x4-3x3-65x2-8x+156

$\begin{aligned} f (x) = 4 x^{4} + 20 x^{3} - 23 x^{2} - 120 x + 144 \end{aligned}$
::f(x) = 4x4+20x3 - 23x2 - 120x+144

$\begin{aligned} f (x) = 9 x^{4} - 226 x^{2} + 25 \end{aligned}$
:x)=9x4-226x2+25

Solve $\begin{aligned} f (x) = 3 x^{4} - x^{2} - 14 \end{aligned}$ by factoring. How many real solutions does this function have? What type of solution(s) could the others be?
::以保理法解决 f( x) = 3x4- x2- 14 。此函数有多少真正的解决方案? 其它的可以是什么类型的解决方案 ?

Review (Answers)
::回顾(答复)

Please see the Appendix.
::请参看附录。

章节大纲

Introduction ::导言

The Remainder Theorem ::遗物定理

The Factor Theorem ::因数定理

The Rational Zero Theorem ::理性的零定理

Descartes's Rule of Signs ::笛卡尔的标志规则

Finding Zeros ::查找零

Examples ::实例

Summary ::摘要

Review ::回顾

Review (Answers) ::回顾(答复)

Introduction
::导言

The Remainder Theorem
::遗物定理

The Factor Theorem
::因数定理

The Rational Zero Theorem
::理性的零定理

Descartes's Rule of Signs
::笛卡尔的标志规则

Finding Zeros
::查找零

Examples
::实例

Summary
::摘要

Review
::回顾

Review (Answers)
::回顾(答复)