代数基本理论

播放段落

Introduction
::导言

播放段落

The Fundamental Theorem of Algebra is the key to answering this question and determining whether finding the solution is worthwhile. The theorem states every polynomial equation has at least one solution.  
::代数的基本理论是回答这一问题和确定找到解决方案是否值得的关键。 该理论说明了每个多元方程式至少有一个解决方案。

播放段落

The Fundamental Theorem of Algebra
::代数基本理论

播放段落

If $\begin{align*}f(x)\end{align*}$ is a polynomial of degree $\begin{align*}n\ge 1\end{align*}$ , then $\begin{align*}f(x)\end{align*}$ has at least one zero in the complex number domain . In other words, there is at least one complex number $\begin{align*}c\end{align*}$ such that $\begin{align*}f(c)=0\end{align*}$ .
::如果 f( x) 是一度 n1, 那么 f( x) 在复数域中至少有 零 。 换句话说, 至少有一个复数 c , 如 f( c) =0 。

播放段落

Several  proofs exist for the Fundamental Theorem of Algebra, but all require much more advanced mathematics. This  theorem is considered to be one of the most important theorems in mathematics. A corollary of this important theorem is the Factorization Theorem. 
::代数基本理论有几种证据存在,但都需要更先进的数学。 这个理论被认为是数学中最重要的理论之一。 这个重要理论的必然结果就是“因子化理论 ” 。

播放段落

The Factorization Theorem:
::因素化理论:

播放段落

If
::如果(如果)

播放段落

$$\begin{align*}f(x)=a_{n}x^{n}+a_{n-1}x^{n-1}+\cdots+a_{1}x+a_{0},\end{align*}$$
:x) = anxn+an- 1xn- 1a1x+a0,

播放段落

where $\begin{align*}a_{n} \ne 0\end{align*}$ , and $\begin{align*}n\end{align*}$ is a positive integer , then
::a++%0, 和 n为正整数的

播放段落

$$\begin{align*}f(x)=a_{n}(x-c_{1})(x-c_{2})\cdots(x-c_{n}),\end{align*}$$
:xx) = an(x-c1)(x-c2) (x-cn),

播放段落

where the numbers $\begin{align*}c_{i}\end{align*}$ are complex numbers. This leads to the n-Roots Theorem.
::数字 ci 是复杂的数字。 这导致 n- Roots 定理 。

播放段落

The n-Roots Theorem
::N -Roots定理

播放段落

If $\begin{align*}f(x)\end{align*}$ is a polynomial of degree $\begin{align*}n\end{align*}$ , where $\begin{align*}n\ne 0\end{align*}$ , then $\begin{align*}f(x)\end{align*}$ has, at most, $\begin{align*}n\end{align*}$ zeros .
::如果 f(x) 是一等n, 其中n0, 那么f(x) 最多为 n0。

播放段落

Notice that this theorem does not restrict that the zeros must be distinct. In other words, multiplicity of the zeros is allowed. For example, the quadratic equation $\begin{align*}f(x)=x^{2}+6x+9\end{align*}$ has one zero, -3, with multiplicity $\begin{align*}k=2\end{align*}$ . In general, if
::请注意此定理没有限制零必须区别。 换句话说, 允许多个零。 例如, f( x) =x2+6x+9 的四方方方程 f( x) =x2+6x+9 有 零 - 3 , 多重 k=2 。 一般来说, 如果

播放段落

$$\begin{align*}f(x)=(x-c)^{k}q(x)\quad\text{and} \quad q(c)\ne0,\end{align*}$$
:xx) = (x-c) kq(x) 和q(c) =0,

播放段落

then $\begin{align*}c\end{align*}$ is a zero of the polynomial $\begin{align*}f\end{align*}$ and of multiplicity $\begin{align*}k\end{align*}$ . For example,
::然后, c 是多面性 f 和多重 k 的零。 例如,

播放段落

$$\begin{align*}f(x)=(x-2)^{3}(x+5)\end{align*}$$
:xx)=(x-2)3(x+5)

播放段落

has 2 as one zero with $\begin{align*}k=3\end{align*}$ and -5 as a zero with $\begin{align*}k=1\end{align*}$ .  
::2 等于 1 0, k=3 和 -5 等于 0, k= 1 。

播放段落

Finding a Polynomial Function with Given Roots
::查找带有给定根的多面函数

播放段落

On the other hand, if you are given the roots of the polynomial, you can create the equation. By substituting each of the zeros into factors and then distributing, zeros can allow us to determine the polynomial function . This process may remind you of using the zeros to determine a quadratic equation. For example, if we are asked to find a 4th-degree polynomial with the roots 1, 6, $\begin{align*}-3\end{align*}$ , and  $\begin{align*}-8\end{align*}$ , we could write  $\begin{align*}f\left(x\right)=(x-1)(x-6)(x+3)(x+8).\end{align*}$
::另一方面,如果给您给定多面形的根根, 您可以创建方程。 通过将每个零替换为因数, 然后分配, 零可以让我们确定多面形函数。 这个过程可以提醒您使用零来决定四面形方程。 例如, 如果我们被要求找到一个四度多面形, 根数 1、 6、 3 和 -8, 我们可以写入 f( x) = (x- 1) (x- 6) (x+3) (x+8) 。

播放段落

Conjugate Pairs Theorem
::共和对等理论

播放段落

If $\begin{align*}f(z)\end{align*}$ is a polynomial of degree $\begin{align*}n\end{align*}$ , with $\begin{align*}n\ne0\end{align*}$ and with real coefficients, and if $\begin{align*}f(z_{0})=0\end{align*}$ , where $\begin{align*}z_{0}=a+bi\end{align*}$ , then $\begin{align*}f(\overline{z_{0}})=0\end{align*}$  such that  $\begin{align*}\overline{z_{0}}\end{align*}$ is the complex conjugate of $\begin{align*}z_{0}\end{align*}$ . 
::如果 f(z) 是一等量 n, 有n0 和真实系数, 如果 f(z0) = 0, 其中z0=a+bi, 那么 f( z0) = 0 , 那么f( z0) = 0 如此复杂, z0 的结合就是 z0 。

播放段落

Recall that the complex conjugate for a complex number  $\begin{align*}a+bi\end{align*}$  is  $\begin{align*}a-bi\end{align*}$ . 
::回顾复杂数字a+bi的复杂共同点是 a-bi。

播放段落

This theorem says that if a complex number is a zero of a polynomial with real coefficients, then its complex conjugate must also be a zero of the same polynomial. In other words, complex roots (or zeros) exist in conjugate pairs for the same polynomial. For example, the polynomial function
::这个理论说,如果一个复合数字是具有实际系数的多元数值的零,那么其复杂的共产体也必须是同一多元系数的零。 换句话说,同一多元系数的复合根( 或零) 存在于同一种复合对配中。 例如, 多元函数

播放段落

$$\begin{align*}f(x)=x^{2}-2x+2\end{align*}$$
:xx) =x2-2x+2

播放段落

has two zeros: one is the complex number $\begin{align*}1+i\end{align*}$ . By the Conjugate Pairs Theorem (also called the Conjugate Root Theorem), $\begin{align*}1-i\end{align*}$ is also a zero of $\begin{align*}f(x)=x^{2}-2x+2\end{align*}$ . We can easily prove that by multiplication :
::具有 2 零 : 1 是 1+ 1 的复合数 。 根据 Conjugate Pairs 理论( 也称为 Conjugate 根理论 ) , 1- i 也是 f( x) =x2 - 2x+2 的零 。 我们很容易通过乘法证明:

播放段落

$$\begin{align*}\left[x-(1+i)\right]\left[x-(1-i)\right] &= (x-1-i)(x-1+i)\\ &= x^2 -x +xi - x +1 - i - xi + i +1\\ &= x^2 -2x + 2\end{align*}$$
::[x-(1+一) [x-(1-一)]=(x-1-(一)-(一)=(x-1-(一)(x-1+一)=x2-(x)-(x)-(x)-(x)-(x)-(x)-(x)-(一)-(一)-(一)-(一)-(一)-(一)][x-(一)-(一)-(一)-(一)(一)(一)=x2-(一)-(x)-(x)-(x)-(x)-(一)-(一)-(一)-(一)-(一)-(一)-(一)-(一)-(一)-(一)-(一)-(一)-1)-(一)-(一)-(一)-(一)-(一)-(一)-(一)-(一)-(一)-(一)-(一)-(一)+)-(一)+)-(一)-(一)-(一)-(一)+)-(一)-(一)-(一)-(一)-(一)-(一)-)(二)-(一)-(一)-)(二)-(一)-(一)-)(一)-)(一)-(一)-)-)-)-(一)-(一)-(一)-)-)-(一)-)-(一)-(一)-(一)-(一)-(一)-(一)-(一)-(一)-(一)-(一)-(一)-(一)-(一)-(一)-(一)-(一)-(一)-(一)-(一)-(一)-(一)-(一)-(一)-(一)-(一)-(一)-(一)-(一)-)-(一)-(一)-(一)-(一)-(一)-(一)-(一)-(一)-(一)-(一)-(一

播放段落

Examples
::实例

播放段落

Example 1 
::例1

播放段落

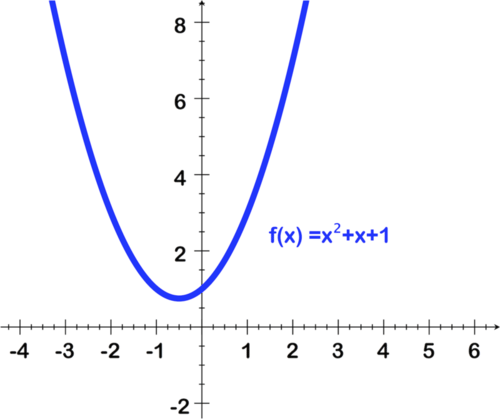
Write $\begin{align*}g(x)=x^{2}+x+1\end{align*}$  in factored form over the complex numbers.
::将 g(x) =x2+x+1 以乘数的乘数形式写成。

播放段落

Solution:
::解决方案 :

播放段落

Step 1: Notice that  $\begin{align*}g(x)\end{align*}$ has no real roots, since its graph has no  $\begin{align*}x\end{align*}$ - intercepts :  
::第1步:注意g(x)没有真正的根根,因为其图形没有 X 界面:

播放段落

Step 2: Using the quadratic formula , the roots of $\begin{align*}g(x)\end{align*}$ are
::第2步:使用四方公式,g(x)的根是

播放段落

$$\begin{align*}x &= \frac{-b \pm \sqrt{b^2-4ac}}{2a}\\ &= \frac{-1 \pm \sqrt{(1)^2-4(1)(1)}}{2(1)}\\ &= \frac{-1 \pm \sqrt{-3}}{2}\\ &= - \frac{1}{2} + \frac{\sqrt{3}}{2}i \ \text{ or } \ - \frac{1}{2} - \frac{\sqrt{3}}{2}i.\end{align*}$$
::-=YTET -伊甸园字幕组=- 翻译组=- 翻译组=- 翻译组=- 翻译组=- 翻译组=- 翻译组=- 翻译组=- 翻译组=- 翻译组=- 翻译组=- 翻译组=- 翻译组=- 翻译组=- 翻译组=- 翻译组=- 翻译组=- 翻译组=- 翻译组=- 翻译组=- 翻译组=- 翻译组=- 翻译组=- 翻译组=- 翻译组=- 翻译组=- 翻译组=-

播放段落

Step 3: W rite  $\begin{align*}g(x)\end{align*}$ in factored form over the complex numbers:
::第3步:以综合数字的系数形式写出 g(x) :

播放段落

$$\begin{align*}g(x)=\left[x-\left(-\frac{1}{2}+\frac{\sqrt{3}}{2}i\right)\right]\left[x-\left(-\frac{1}{2}-\frac{\sqrt{3}}{2}i\right)\right].\end{align*}$$
::g(x)=[x-(-12)-(-12)-32i) [x-(-)-12)-32i)]。

播放段落

Example 2
::例2

播放段落

Find a polynomial with real coefficients of minimum degree with  the zeros: $\begin{align*}\frac{-1}{3}, 1-i\end{align*}$ and $\begin{align*}2i\end{align*}$ .
::找到一个具有最低程度实际系数的多元系数,零为:-13,1-i和2i。

播放段落

Solution:
::解决方案 :

播放段落

Since the numbers $\begin{align*}2i\end{align*}$ and $\begin{align*}1-i\end{align*}$ are zeros,  then their conjugate pairs must also be zeros by  the Conjugate Pairs Theorem.  Thus,  $\begin{align*}-2i\end{align*}$ and $\begin{align*}1+i\end{align*}$ must also be roots of  $\begin{align*}f(x)\end{align*}$ . Therefore ,
::由于数字2i和1-i为零,那么它们的对等配对也必须是“对等合议定理”中的零。因此,-2i和1+i也必须是f(x)的根。因此,

播放段落

$$\begin{align*}f(x)= \left ( x+\frac{1}{3} \right )[x-(1-i)][x-(1+i)][x-(2i)][x-(-2i)].\end{align*}$$
:xx)=(x+13)[x-(1-)(一)][x-(1+一)][x-(1+一)][x-2(一)][x-(一)][x-(-)(二))]。

播放段落

Simplify:
::简化 :

播放段落

$$\begin{align*}f(x) = \left ( x+\frac{1}{3} \right )(x-1+i)(x-1-i)(x-2i)(x+2i).\end{align*}$$
::f(x) = (x+13) (x-1+1)(x-1-i)(x-2i)(x+2i) 。

播放段落

After multiplying,
::乘以后,

播放段落

$$\begin{align*}f(x)=\frac{1}{3}(3x^{5}-5x^{4}+16x^{3}-18x^{2}+16x+8),\end{align*}$$
::f(x) = 13( 3x5 - 5x4+16x3_ 18x2+16x8)

播放段落

which is a 5th-degree polynomial. Notice that the total number of zeros is also 5.
::注意零的总数也是5。

播放段落

Example 3
::例3

播放段落

What is the multiplicity of each zero of the polynomial below?
::下面每个零的多元体的多重性是多少?

播放段落

$$\begin{align*}g(x)=x^{4}-6x^{3}+18x^{2}-54x+81\end{align*}$$
::g(x) =x4 - 6x3+18x2 - 54x+81

播放段落

Solution:
::解决方案 :

播放段落

Step 1: Using a graphing calculator or program or the Rational Zero Theorem, it can be determined that $\begin{align*}x=3\end{align*}$ is a zero of $\begin{align*}g(x)\end{align*}$ . By  synthetic division ,
::第1步:使用图形计算计算器或程序或理性零理论,可以确定x=3为g(x)0。按合成部分分列,

$$\begin{align*} \ 3 \ \big ) \overline{1 \ -6 \ \ 18 \ -54 \ \ \ \ 81\;}\\ \quad \ \ \underline{\downarrow \ \ \ 3 \ -9 \ \ \ \ 27 \ -81}\\ \quad \ \ 1 \ -3 \ \ \ 9 \ -27 \ \ \ \ \ 0\end{align*}$$

播放段落

$$\begin{align*}g(x)=x^{4}-6x^{3}+18x^{2}-54x+81=(x-3)(x^{3}-3x^{2}+9x-27).\end{align*}$$
::g(x) =x4-6x3+18x2-54x+81=(x-3)(x3-3x2+9x-27)。

播放段落

Step 2: Using synthetic division again on the resulting quotient, $\begin{align*}x=3\end{align*}$  is seen to be a zero of multiplicity 2:
::第2步:在由此得出的商数上再次使用合成分割法, x=3 被看成是多元值的零:

$$\begin{align*} \ 3 \ \big ) \overline{1 \ -3 \ \ 9 \ -27}\\ \underline{\downarrow \ \ 3 \quad 0 \quad 27}\\ \quad \ \ 1 \ \ \ \ 0 \ \ \ 9 \ \ \ \ \ 0\end{align*}$$

播放段落

$$\begin{align*}g(x) &= (x-3)(x-3)(x^2+9)\end{align*}$$
::g(x) = (x-3) (x-3) (x-3) (x2+9)

播放段落

Step 3: Factor $\begin{align*}x^2+9\end{align*}$  over the complex numbers:
::第3步:复数乘以x2+9:

播放段落

$$\begin{align*}g(x) &= (x-3)^2(x-3i)(x+3i). \end{align*}$$ Then, 3 has multiplicity 2, or  3 is said to be a  double zero, and $\begin{align*}3i\end{align*}$ and $\begin{align*}-3i\end{align*}$ are each zeros with multiplicity 1.
::g(x) = (x-3) 2(x-3i)(x+3i) 。 那么, 3 的多重值为 2, 或 3 据说是 双 0 , 而 3 i 和- 3i 则是 多个 1 的每个零 。

播放段落

Example 4
::例4

播放段落

Identify or estimate the values of the zeros and state their multiplicities for 
$\begin{align*}y = (x + 2)^2(x - 1).\end{align*}$
::确定或估计零值,并说明y=(x+2)2(x-1)的倍数。

播放段落

Solution:
::解决方案 :

播放段落

To identify the roots and their multiplicities:
::为了查明根源及其多重性:

播放段落

Step 1: Set the function equal to 0:  

$$\begin{align*}(x + 2)(x + 2)(x - 1) = 0.\end{align*}$$
::第1步:将函数设为 0x+2)(x+2)(x-1)=0) 。

播放段落

Step 2: Solve. The roots then are $\begin{align*}x = 1\end{align*}$ and  $\begin{align*}x = -2\end{align*}$ . 
::步骤 2: 解决。 根为 x=1 和 x @ @ @% 2 。 then the root is x=1 and x @% 2 。

播放段落

Step 3: Since the $\begin{align*}x = -2\end{align*}$ root appears twice, it has a multiplicity of 2, whereas the $\begin{align*}x = 1\end{align*}$ root appears only once, so its multiplicity is 1.
::第3步:由于 x%2 根出现两次,其多重性为2, 而 x=1 根只出现一次, 因此其多重性为 1 。

播放段落

Example 5
::例5

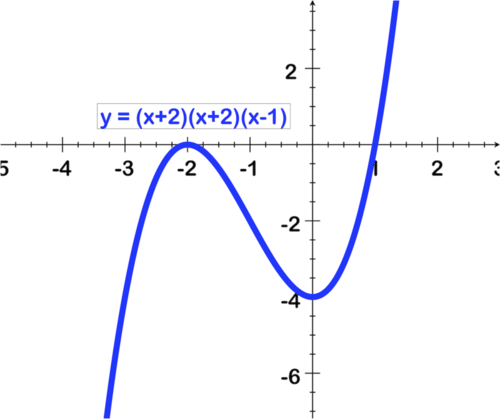
播放段落

Identify the zeros for the function graphed below and state their multiplicities:
::标明以下图表显示的函数的零,并说明其多功能性:

播放段落

Solution:
::解决方案 :

播放段落

Step 1: Identify points where the function crosses the  $\begin{align*}x-axis\end{align*}$ . On this graph, the function passes through at the root  $\begin{align*}x = 1.\end{align*}$
::步骤 1: 确定函数横越 x - 轴的点。 在此图中, 函数在 root x=1 处通过 root x=1 。

播放段落

Step 2: Identify points where the function  touches the  $\begin{align*}x-axis\end{align*}$  but does not cross. This occurs at  the root $\begin{align*}x = -2\end{align*}$ . If a root has an even multiplicity, it will not intersect but will turn away from t he axis, and if it has an odd multiplicity, it will pass through.
::第2步:确定函数触碰 x - 轴但未交叉的点。 根 x\\\\\ 2 发生这种情况。 如果根有偶数, 根不会交叉, 但它会从轴中转开, 如果有奇数的多重, 它会通过 。

播放段落

Step 3:  The zeros of this function are 1 with multiplicity 1, and -2 with multiplicity 2. Note that this makes sense as it is the same function as the previous example.
::第3步:本职能的零是1, 多重1, 多重2。 注意,这与上一个例子的相同功能是有道理的。

播放段落

Example 6
::例6

播放段落

Find a polynomial of degree 5 with real coefficients and the zeros: 1 (multiplicity 2), $\begin{align*}-2\end{align*}$ , and $\begin{align*}-2i\end{align*}$ .
::找到具有实际系数和零位数的5度多元值:1(多重2)、-2和-2i。

播放段落

Solution:
::解决方案 :

播放段落

Step 1: Create the factors for the given zeros and add the conjugate of -2i:
::第1步:为给定的零创建系数,并加上 -2i的组合:

$$\begin{align*}(x - 1)(x + 2)(x - 1)(x + 2i)\end{align*}$$

$$\begin{align*}(x - 1)(x - 1)(x + 2)(x + 2i)(x - 2i).\end{align*}$$

播放段落

Step 2:  Multiply:

$$\begin{align*}f(x)=x^5 + x^3 + 2x^2 - 12x + 8.\end{align*}$$
::第2步:乘以: f(x)=x5+x3+2x2-12x+8。

播放段落

Summary
::摘要

播放段落
• The Fundamental Theorem of Algebra guarantees that a polynomial of degree  $\begin{align*}n\geq1\end{align*}$  has at least one complex zero.
  ::代数的基本理论保证,一等一(n1)至少有一个复合零。
播放段落
• Its corollaries provide tools to find the zero:
  播放段落
  • The Factorization Theorem states that a polynomial of degree  $\begin{align*}n\end{align*}$  can be factored over the complex numbers:   $\begin{align*}f(x)=a_{n}(x-c_{1})(x-c_{2})\cdots(x-c_{n}).\end{align*}$  
    ::保理学理论指出,在复合数字(f(x)=an(x-c1)(x-c2))\(x-cn)\(x-cn))上,可乘以多度尼。
  播放段落
  • The Conjugate Pairs Theorem states that if a polynomial has real coefficients, and   $\begin{align*}z_{0}=a+bi\end{align*}$  is a zero, then  $\begin{align*}z_{0}=a-bi\end{align*}$  is also a zero.
    ::" 共产物对角理论 " 指出,如果多面体具有实际系数,而z0=a+bi为零,那么z0=a-bi也为零。
  
  ::其卷轴提供了找到零的工具: 系数化理论指出, 复数( f( x) = an( x- c1)( x- c2) ) {( x- cn) ) = (x- c2) {( x- cn) ) 中, 复数线提供找到零的工具 。 该理论指出, 如果多元值有实际系数, z0=a+bi 是0, 那么z0=a- bi 也是0 。 </span> </li> <button class="play-button btn btn-success" style="float: right;" value="@s"> 播放段落 </button> <li> <button class="play-button btn btn-success" style="float: right;" value="@s"> 播放段落 </button> <p id="x-ck12-ZTY5ZTUyMTJkODk5NjJjMjU5NjZjMGE0M2YzZTUyZGY.-wfn"> The  <span class="x-ck12-mathEditor" data-contenteditable="false" data-edithtml="FASD4geBnAHBDAdgAgMYBt7WgXgEQBOApogCZHGkC0AtvAC4AWeyAlqfkaa/fAEboiAWQbNk0egE9B+AGYB7RPSrRWALyIAuZACYALLAAeAbjwA+UBCshIrRLACu9ZFNhF89IofosMWXHiyrAQSLl7OdHZ88obIjFgAKuEsiPA07nh0TCzs+FlisPKq9KyK+ACMvg4S8jRUAO7sTPgAzDpVNXWMRKwA5oz0re3I8E7yqLWwgp748rKyLBLSGY2kTNrlAOxGxnE9/fTabTssAG7w6A4ZiOaW1mCQAPRwSBb3YEAAA" data-math-class="x-ck12-math" data-mathmethod="inline" data-tex="n"> <span class="MathJax_Preview" style="color: inherit;"> <span class="MJXp-math" id="MJXp-Span-1520"> <span class="MJXp-mtable" id="MJXp-Span-1521"> <span> <span class="MJXp-mtr" id="MJXp-Span-1522" style="vertical-align: baseline;"> <span class="MJXp-mtd" id="MJXp-Span-1523" style="text-align: right;"> <span class="MJXp-mi MJXp-italic" id="MJXp-Span-1524"> n </span> </span> </span> </span> </span> </span> </span> <span class="MathJax_SVG MathJax_SVG_Processing" id="MathJax-Element-92-Frame" style="font-size: 100%; display: inline-block;" tabindex="-1"> </span> <script id="MathJax-Element-92" type="math/tex"> \begin{align*}n\end{align*} -Roots Theorem states that if $\begin{align*}f(x)\end{align*}$ is a polynomial of degree $\begin{align*}n\end{align*}$ , where $\begin{align*}n\ne 0\end{align*}$ , then $\begin{align*}f(x)\end{align*}$ has at most  $\begin{align*}n\end{align*}$ zeros.
  ::n-RootsTheorem 表示,如果 f(x) 是一等n的多元度 n, 那么 f(x) 最多为 n0 。
  
  ::n-RootsTheorem 表示,如果 f(x) 是一等n的多元度 n, 那么 f(x) 最多为 n0 。

播放段落

Review
::回顾

播放段落

For 1-4, find the polynomial with the given roots:
::1 - 4, 找到与给定根的多面性 :

播放段落

1. 2 (with multiplicity 2), 4 (with multiplicity 3),  $\begin{align*}1, \sqrt{2}i, -\sqrt{2}i\end{align*}$ .
::1. 2,2,4(3),1,2i,2i。

播放段落

2. 1, -3 (with multiplicity 3),  $\begin{align*}-1, \sqrt{3}i, -\sqrt{3}i.\end{align*}$
::2. 1-3(多重3),-1-3i,3i。

播放段落

3. 5 (with multiplicity 2), -1 (with multiplicity 2),  $\begin{align*}2i, -2i.\end{align*}$
::3. 5(多重2),-1(多重2),2i,-2i。

播放段落

4.  $\begin{align*}i, -i, \sqrt{2}i, -\sqrt{2}i\end{align*}$
::4. i,i,2i,2i

播放段落

Factor  each polynomial completely. Use the various theorems from this section, synthetic division, and/or a calculator or graphing program to solve.
::每个多数值系数的系数 。 使用本节的不同定理、 合成项和/ 或计算器或图形程序解析 。

播放段落

5.  $\begin{align*}f(x)=x^5+4x^4-2x^3-14x^2-3x-18\end{align*}$
::5. f(x)=x5+4x4-2x3-14x2-3x-18

播放段落

6.  $\begin{align*}g(x)=x^4-1\end{align*}$
::6. g(x)=x4-1

播放段落

7.  $\begin{align*}h(x)=x^6-12x^5+61x^4-204x^3+532x^2-864x+576\end{align*}$
::7. h(x)=x6-12x5+61x4-204x3+532x2-864x+576

播放段落

8.  $\begin{align*}j(x)=x^7-11x^6+49x^5-123x^4+219x^3-297x^2+243x-81\end{align*}$
::8. j(x) =x7- 11x6+49x5 - 123x4+219x3-297x2+243x- 81

播放段落

9.  $\begin{align*}k(x)=x^5+3x^4-11x^3-15x^2+46x-24\end{align*}$
::9. k(x) =x5+3x4- 11x3- 15x2+46x-24

播放段落

10.  $\begin{align*}m(x)=x^6-12x^4+23x^2+36\end{align*}$
::10.(x)=x6-12x4+23x2+36

播放段落

11.  $\begin{align*}n(x)=x^6-3x^5-10x^4-32x^3-81x^2-85x-30\end{align*}$
::11. n(x)=x6-3x5-10x4-32-81x2-85x-30

播放段落

12.  $\begin{align*}p(x)=x^6+4x^5+7x^4+12x^3-16x^2-112x-112\end{align*}$
::12.p(x)=x6+4x5+7x4+12x3-16x2-112x-112

播放段落

13. How can you tell the number of roots that a polynomial has from its equation?
::13. 你如何从多元等式中分辨出根数?

播放段落

14. Explain the meaning of the term “multiplicity.”
::14. 解释 " 多重性 " 一词的含义。

播放段落

15. A polynomial with real coefficients has one root that is $\begin{align*}\sqrt{3}i \end{align*}$ .  What other root(s) must the polynomial have?
::15. 具有实际系数的多元系数有一个根,即3i。 多元系数还必须有其他根吗?

播放段落

Review (Answers)
::回顾(答复)

播放段落

Please see the Appendix.
::请参看附录。