相近的多元函数实际零位数
章节大纲
-
Introduction
::导言In elementary algebra courses, graphs are often constructed by plotting points and then connecting the points. In precalculus, the points are used to fine-tune a graph. To do this , the 1st step is to classify a function into a family, and choose the appropriate characteristics of that family to build a graph. Interestingly , for many graphs, connecting the points would not be the best choice. To see why, a ssume that a graph needs to be constructed for a function, . Three points are plotted. The following graphs are possibilities:


This situation demonstrates the need to know more about the function's characteristics to be able to make this decision. It also requires some theorems to know under which conditions the mathematician can "connect the dots" to complete the sketch of a graph.
::这种情况表明需要更多地了解函数的特性才能作出这一决定。 还需要一些理论家知道数学家在何种条件下可以“ 连接点” 完成图表的草图。Intermediate Value Theorem
::中间值定理The provides the conditions to sketch a continuous graph between the plotted points. It requires that a function be continuous. R ecall that an informal definition of continuous is that a function is continuous over a certain interval if it has no breaks, jumps, asymptotes, or holes in that interval. Polynomial functions are continuous for all real . Rational functions are often not continuous over the set of real numbers because they do have the discontinuities, asymptotes, or holes in the graph.
::提供在绘图点之间绘制连续图表的条件。 它要求函数是连续的。 提醒注意, 一个连续的非正规定义是,如果该连续的函数没有间断、 跳跃、 空洞或洞洞, 则该连续的间隔是连续的 。 对于所有真实的 x 来说, 多功能是连续的 。 逻辑函数通常不是连续的, 因为它们在图形中存在不连续性、 空洞或洞洞 。Knowing that a function is continuous over some interval allows a mathematician to use the Intermediate Value Theorem.
::了解某函数在一定间隔[a,b]内具有连续性,可使数学家使用中间值理论。Intermediate Value Theorem
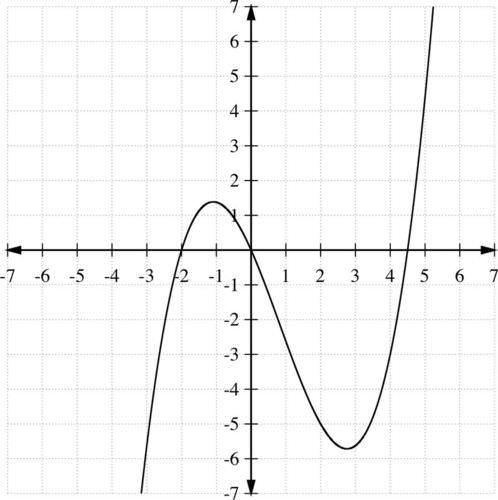
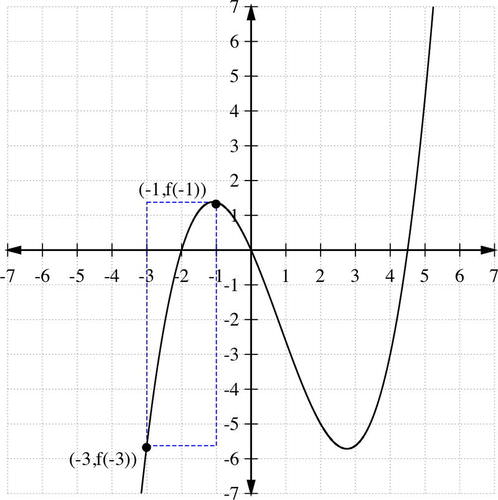
::中间值定理If is continuous on some interval and is between and , then there is some such that .The following graphs highlight how the Intermediate Value Theorem works. Consider the graph of the function on the interval [-3, -1]:
::以下图表突出显示中间值定理是如何工作的。 考虑间隔[ 3 - 1] 的函数 f( x) = 14( x3 - 5x22 - 9x) 的图形 :and . Since is a polynomial, thus continuous for all real values of , then a continuous curve can be drawn from to .
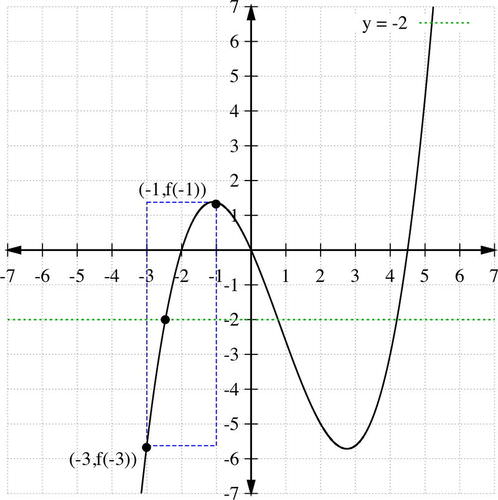
::f(-3) 5.625和f(-1)=1.375。f(x)是多元的,因此对x的所有实际值都是连续的,因此,可以从(-3)至(-1)至(-1)至(-1)至(1)至(3)至(3)至(5)至(3)至(3)至(3)至(3)至(3)至(3)至(3)至(1)至(3)至(3)至)。This theorem can be used to estimate the coordinates of points on the graph. For example, any -value between -5.625 and 1.375, say , corresponds to some value on the interval [-3, -1].
::此定理可用于估算图中点的坐标。 例如, y 值在 -5. 625 和 1. 375 之间的任何 Y 值, 例如 y = 2, 与间距[ 3 - 1] 上的一些 x - 值相对应 。The Bounded Roots Theorem
::断根定理The Bounded Roots Theorem is a corollary to the Intermediate Value Theorem:
::深根定理是中间值定理的必然结果:Bounded Roots Theorem
::深根定理If is continuous on and there is a sign change between and (that is, is positive and is negative, or vice versa), then there is a such that .The Bounded Roots Theorem is a corollary to the Intermediate Value Theorem because it is simply a special case where .
::深根定理是中间值定理的必然结果,因为它只是n=0的特殊案例。In the previous example, , since and , and is continuous on , then has a root on the given interval. The graph estimates the root to be at .
::在上个例子f(x)=14(x3-5x22-9x)中,由于 f(-3) <0和 f(-1)>0和 f(x)>0和 f(x)是连续的[-3)-1], f(x)在给定间隔上有一个根。图中估计根在 x%2 。Approximate Zeros of Polynomial Functions
::近乎零多元函数T he Intermediate Value Theorem is a simple but extremely powerful theorem. One of the most critical applications of the theorem is illustrated here with bounded roots:
::中间值定理是一个简单但极强的定理。Given a continuous function ,
::给定连续函数 g( x) ,-
Find two points such that
and
. Once these two points are found, iterate, using the steps below to home in on the root of
on the interval
. (Note, we will assume
; the same algorithm works with minor adjustments if the opposite is true.)
::查找两个点, 如 g(a) < 0 和 g(b) > 0 。 一旦发现这两个点, 就会在 [a, b] 间距上使用 g(x) 根根部的下到家的步数。 (注意, 我们将假设 g(b) > g(a) ; 如果相反, 同样的算法会稍作调整 。) -
Evaluate
.
-
If
, then the root is
.
::如果 g( a+b2) =0, 那么根就是 x=a+b2 。 -
If
, replace
with
and repeat steps 1-2 using
::如果 g(a+b2) < 0, 将 a 替换为 a+b2, 并使用 [a+b2, b] 重复步骤1-2。 -
If
, replace
with
and repeat steps 1-2 using
::如果 g(a+b2) >0, b 替换为 a+b2, 并使用 [a, a+b2] 重复步骤1-2。
::如果 g(a+b2) =0,则根为 x=a+b2=0,如果 g(a+b2) < 0,则根为 x=a+b2 < 0, 替换为 a+b2, 并使用 [a+b2, b] 重复步骤1-2。如果 g(a+b2) >0, 则用 a+b2 替换 bb2, 并使用 [a, a+b2] 重复步骤1-2。 -
If
, then the root is
.
This algorithm will not usually find the exact root of , but the root found will be within a tolerable error range. For example, if this process is repeated enough times so that , the root of is correct within 0.005.
::此算法通常不会找到 g( x) 的确切根, 但所找到的根将位于可容忍的错误范围之内。 例如, 如果此进程重复足够多次, 使 {a- b\\\\\ 0.01} g( x) 根在 0.005 内正确 。Examples
::实例Example 1
::例1Show that has at least one root in the interval [1, 2].
::显示 f( x)\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\Solution:
::解决方案 :Since is a polynomial, it is continuous on [1, 2] . and . Since , there must exist some point such that by the Intermediate Value Theorem or the Bounded Roots Theorem. Therefore, has a root in (1, 2).
::由于 f(x) 是多元的, 它在 [1、2] . f(1)=2 和 f(2) 14 上是连续的。 由于 n=0\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\Example 2
::例2The table below shows several sample values of a polynomial :
::下表显示多个多边 p(x) 的多个样本值:
::-4-2014-68101518p(x)44.156.62-4.12-4.91.160-8.74-24.07-49.893.41Based on the information in the table,
::根据表中的资料,(a) What is the minimum number of roots of ?
:a) p(x) 的最低根数是多少?
(b) What are bounds on the roots of identified in (a)?
:b) 在(a)中查明的p(x)的根部有哪些界限?
Solution:
::解决方案 :S ince is a polynomial, it is continuous everywhere. Use the Bounded Roots Theorem to identify roots by looking at intervals where changes sign.
::由于 p( x) 是多元的, 它在任何地方都是连续的 。 使用深根定理通过查看 p( x) 更改符号的间隔来识别根 。(a) There are four sign changes of in the table, so has a minimum of four roots.
:a) 表中p(x)有4个符号变化,因此p(x)至少有4根根。
(b) The roots are in the following intervals and the table shows one root is at .
:b) 根在以下间隔x[-2,0],x[1,4],x[15,18],表格显示一个根在x=6。
Example 3
::例3Show the 1st five iterations of finding the root of using the starting values and .
::使用起始值 a=0 和 b=2 显示查找 h(x) =x2 - x- 1 根的首五个迭代Solution:
::解决方案 :Step 1: Since is continuous, verify that there is a root between and . and so by the Bounded Roots Theorem there is a root in the interval [0, 2]. Check . Since the root is between and . Continue with the new interval, [1, 2].
::步骤 1: 由于 h( x) 是连续的, 校验 x=0 和 x=2. h( 0) @% 1 和 h(2)=1 之间有根, 因此通过有界根的定理, 在间隔 [ 0, 2] 中有一个根 。 check h( 0+22)=h(1)\\\\\\ 1. 由于~ 1 < 0, 根在 x=1 和 x=2 之间, 根在 x=1 和 x=2 之间 。 继续使用新间隔, [ 1, 2] 。Step 2: Now the interval is [1, 2]. . Since , choose the interval [1.5, 2].
::步数 2: 现在的间隔是 [1、2]. h(1+22)=h(1.5) @ @%0. 25。 从- 0. 25 < 0, 请选择间隔 [1.5、 2] 。Step 3: . Since , choose the interval [1.5, 1.75].
::第3步:h(1.5+22)=h(1.75)=0.31。自0.31[0.31],请选择间隔[1.5、1.75]。Step 4: . Since , the root is between 1.5 and 1.625.
::第4步:h(1.5+1.752)=h(1.625)=_0.002。自0.02>0以来,根在1.5至1.625之间。Step 5: . Since , we know the root is between 1.5620 and 1.625.
::步骤5:h(1.5+1.6252)=h(1.5620)=0.12。从-0.12 < 0开始,我们知道根在1.5620到1.625之间。This example shows that after five iterations, the possible location of the root, the midpoint of the interval, is accurate within approximately 0.03 units.
::这个例子显示,在五个迭代之后,根的可能位置,即间距的中点,在大约0.03个单位内准确无误。Summary
::摘要-
Intermediate Value Theorem
::中间值定理If is continuous on some interval and is between and , then there is some such that .
::如果f(x)在一定的间隔[a,b]是连续的,而n在f(a)和f(b)之间,那么就有一些f(c)=n的c[a,b]。
::如果f(x)在一定的间隔[a、b]和n在f(a)和f(b)之间时是连续的,那么就有一些f(c)=n的c[a、b]。 -
Bounded Roots Theorem
::深根定理If is continuous on and there is a sign change between and (that is, is positive and is negative, or vice versa), then there is a such that .
::如果f在[a,b]上是连续的,而且f(a)和f(b)(即f(a)为正数,f(b)为负数,或f(b)为负数,或反之亦然)之间有符号变化,那么就有一个f(c)=0的c(a),b)为f(c)=0。
::如果 f 在 [a, b] 上是连续的, f(a) 和 f(b)(即 f(a) 是正数, f(b) 是负数, f(b) 是负数, 反之亦然), f(c) =0 之间有符号变化,则有 c(a), b) 等於 f(c)=0。
Review
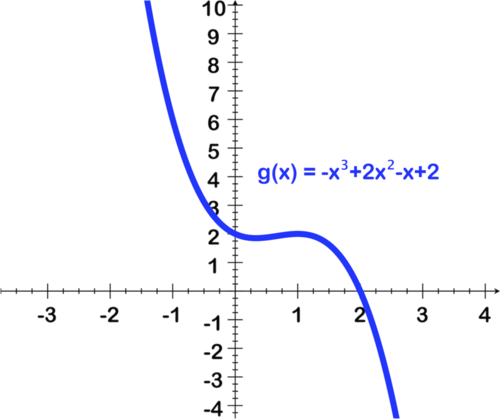
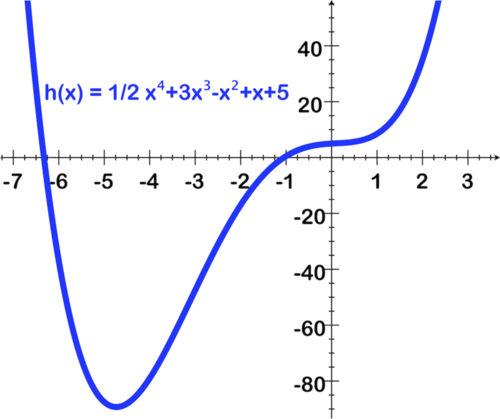
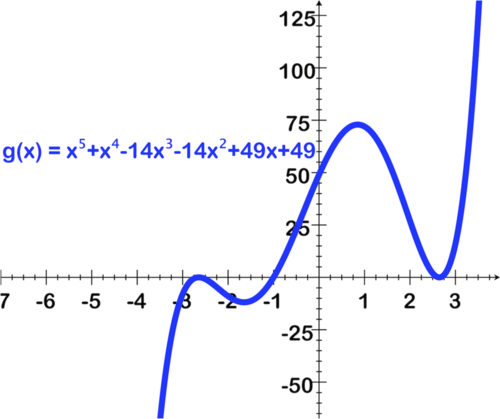
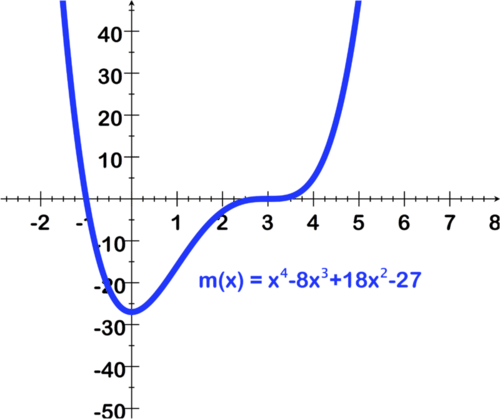
::回顾For questions 1–5, use the image of the graph and accompanying equation to find the following:
::对于问题1-5,使用图表的图象和相应的方程式来查找:- a. Leading coefficient and degree of the polynomial,
- b. Number of real zeros and their approximate values using the graph,
- c. Number of imaginary zeros.
1.
2.
3.
4.
5.
For questions 6–10, use the Intermediate Value Theorem to show the bounds on the roots of each function. The bounds should be integer values.-
:xx)=2x3-3x+4
-
::g(x) =========================================================================================================================================================================================12===12 -
::h(x) = 12x4 - x3 - 3x2+1 -
is a polynomial and selected values of
are given in the following table:
:kx) 是多元值, 下表给出了 k(x) 的选定值 :
::x-3-2-2-1 1 2 3k(x)-23.5-10.5-1.5-1-23.5-
Stephen argues the function
has two zeros based on the following table and an application of the
Bounded Roots
Theorem. What is faulty about Stephen's reasoning?
::Stephen 争论 r( x) = 4x+1x+3.5 函数基于下表和 Bounded Roots 理论的应用有两个零。 Stephen 的推理有什么问题?
::x-5-4-3-2-1 0 1 2 3 4r(x)12.67 30-22-4.67-1.200.291.111.642.02。For problems 11–12, apply the numerical algorithm five times to find a bound on the zeros of the following functions, given the indicated starting values. Give a final estimate for the zero.
::对于问题 11 - 12, 使用数字算法五次在以下函数的零值上找到一个约束值, 以显示起始值 。 给出 0 的最后估计值 。-
on
::[ 0, 1] 的 k(x) =x4- 3x+1 -
on
:x) [1,3] b (x) 0.1x5+3x3-3-5x2
Review (Answers)
::回顾(答复)Please see the Appendix.
::请参看附录。 -
Find two points such that
and
. Once these two points are found, iterate, using the steps below to home in on the root of
on the interval
. (Note, we will assume
; the same algorithm works with minor adjustments if the opposite is true.)