化合物利息

播放段落

An investor is considering two investments. The 1st choice is a capital investment and pays a guaranteed 5.4% annually. The 2nd choice is a savings account that pays 5.3% interest compounded daily. The investor plans to choose the 1st investment, but is this the best choice?    
::投资者正在考虑两项投资。 第一项选择是资本投资,每年支付5.4%的保证金。 第二项选择是每天支付5.3%利息的储蓄账户。 投资者计划选择第一项投资,但这是最好的选择吗?

播放段落

Compound Interest
::化合物利息

播放段落

Nearly all investment accounts can be established so that the interest is compounded. This means the investor is paid interest on any funds in an account, even if they were earnings on the original investment. Every investor needs to understand the mathematical effects of compounding. First, the formula :
::几乎所有投资账户都能够建立,这样利息就会变本加厉。 这意味着投资者可以在账户中的任何基金上获得利息,即使这些基金是原始投资的收益。 每个投资者都需要理解复合的数学影响。 首先,公式:

播放段落

$$\begin{align*}A(t) = p \cdot \left(1 +\frac{r}{n}\right)^{nt},\end{align*}$$
::A(t) =p( 1+rn) ,

播放段落

where
::何 地

播放段落
• $\begin{align*}A(t)\end{align*}$  is the accumulated value of the investment in the account after  $\begin{align*}t\end{align*}$  years.
  ::A(t) 系指在t年之后在该账户中投资的累计价值。
播放段落
• $\begin{align*}p\end{align*}$  is the principal, or amount originally invested. 
  ::p 是本金,或最初投资的金额。
播放段落
• $\begin{align*}r\end{align*}$  is the annual interest rate .
  ::r 是年利率。
播放段落
• $\begin{align*}n\end{align*}$  is the number of times that the interest is compounded each year. This means the interest is paid in  $\begin{align*}n\end{align*}$  equal payments throughout the year.
  ::n 表示每年利息复数的倍数。这意味着全年以n等额支付利息。
播放段落
• $\begin{align*}t\end{align*}$  is the number of years that the money remains in the account.
  ::t 是钱留在账户里的年数。

播放段落

If the amount of money is compounded quarterly, then $\begin{align*}n=4\end{align*}$ .  If the amount of money is compounded monthly , then  $\begin{align*}n=12\end{align*}$ . Notice that   $\begin{align*}t\end{align*}$  is determined in years, so 6 months would mean  $\begin{align*}t=0.5\end{align*}$ . 
::如果货币金额是每季度一次,那么n=4。如果货币金额是每月一次,那么n=12。请注意,t是按年份确定的,所以六个月意味着t=0.5。

播放段落

Compound interest yields more interest because throughout the year,  the principal includes both the initial principal and the interest earnings for the year. 
::复利产生更多的利息,因为在整个一年中,本金包括当年的初始本金和利息收入。

 

  

播放段落

Continuously Compounded Interest
::连续增加的利息

播放段落

In finance, interest that is calculated continuously is often discussed. This type of interest is called  continuously compounded interest . Similar to population growth and decay, an exponential function is used to simulate the continuous growth of the interest. The formula for continuously compounded interest is 

$$\begin{align*}A(t)=p{e}^{rt}.\end{align*}$$
::在金融方面,经常讨论连续计算的利息。这类利息被称为连续的复合利息。与人口增长和衰变相似,用指数函数模拟利息的持续增长。持续复合利息的公式是A(t)=pert。

  

播放段落

Examples
::实例

播放段落

Example 1
::例1

播放段落

Use the formula for compound interest to determine the amount of money in an investment after 20 years, if $2,000 is invested, and the interest rate is 5% compounded annually.
::如果投资2 000美元,则使用复合利息公式确定20年后投资金额,年利率为5%。

播放段落

Solution:
::解决方案 :

播放段落

$$\begin{align*}A(20)& = 2,\!000{(1.05)}^{20}\\ A(20)&\approx 5,\!306.60\end{align*}$$
::A(20)=2,000(1.05)20A(20)=5,306.60

播放段落

The investment will be worth $5,306.60.
::投资价值5 306.60美元

播放段落

Example 2
::例2

播放段落

How long will it take for $2,000 invested at 5% compounded annually to reach $7,000?
::2 000美元的投资需要多久才能达到7 000美元?

播放段落

Solution:
::解决方案 :

播放段落

$$\begin{align*}2,\!000(1.05)^t &= 7,\!000\\ 1.05^t &= 3.5\\ \ln{1.05^t} &=\ln{3.5}\\ t\cdot \ln{1.05} &= \ln{3.5}\\ t &= \frac{\ln{3.5}}{\ln{1.05}}\\ t &\approx 25.677 \end{align*}$$
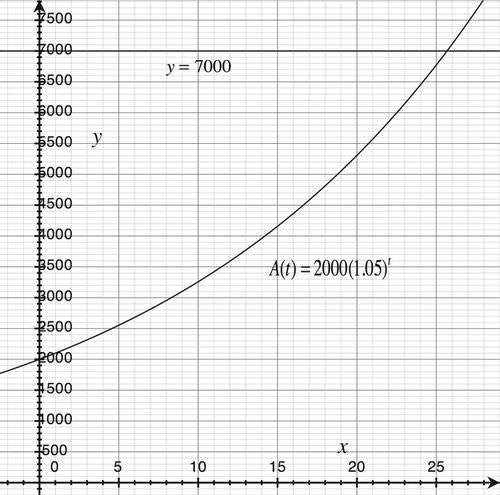
::2 000(1.05)t= 7,0001.05t= 3.5ln1.05t= 0.5t@ 3.5t@@@1.05=ln @ 1.05t= 0.5n_ @1.05t= 1.05t_25.677)

播放段落

This example could also be solved by graphing the function $\begin{align*}A(t) = 2,\!000(1.05)^t\end{align*}$  and the horizontal line $\begin{align*}y=7,\!000\end{align*}$ . The graph shows account values for a 28-year period. The intersection of the exponential function for compound interest and the horizontal line can be used to estimate the year when the account reaches $7,000. 
::也可以通过图形化函数 A(t) = 2 000(1.05t) 和水平线 y= 7 000 来解决这个问题。图形显示28年期间的账户值。复合利息的指数函数和水平线的交叉点可用于估计账户达到7 000美元的年份。

播放段落

The intersection point is approximately (25.7, 7000), so it would take almost 26 years for the investment to reach $7,000.
::交叉点约为(25.7,700美元),因此投资需要将近26年才能达到7 000美元。

播放段落

Example 3
::例3

播放段落

What is the value of an investment after 20 years, if $2,000 is invested at the interest rate 5% compounded continuously?
::如果以5%的利率连续投资2 000美元,20年后投资的价值是什么?

播放段落

Solution:
::解决方案 :

播放段落

Using the formula for compound interest: 
::使用复合利益公式:

$$\begin{align*}A(20) &= 2,\!000{e}^{0.05(20)}\\ A(20) &= 2,\!000{e}^{1}\\ A(20)& \approx {5,\!436.56}.\end{align*}$$  

播放段落

So, the value of the investment is $5,436.56.
::因此,投资的价值是5 436.56美元。

播放段落

Example 4
::例4

播放段落

Return to the problem from the Introduction, concerning an investor who is considering two investments. The 1st choice pays a guaranteed 5.4% annually, and the 2nd choice pays 5.3% interest compounded daily. Which is  the best choice?  
::回到《导言》的问题,即一个投资者在考虑两项投资。 第一选择每年支付5.4%的保证金,第二选择每天支付5.3%的利息,而第二选择每天支付5.3%的利息。 哪种是最好的选择?

播放段落

Solution:
::解决方案 :

播放段落

To answer the original problem, assume $20,000 is invested and calculate the values of each account after one year. The choices are:
::为了解决最初的问题,假设投资20 000美元,并在一年后计算每个账户的价值。

播放段落

First choice:     $\begin{align*}A(1)=20,\!000{(1+.054)}^{1}=21,\!080.00.\end{align*}$
::第一种选择:A(1)=20,000(1+.054)1=21,080.00。

播放段落

Second choice:   $\begin{align*}A(1)=20,\!000\left(1+\frac{0.053}{365}\right)\approx{21,\!088.51}.\end{align*}$  

::第二选择:A(1)=20,000(1+0.053365) 21,088.51。

播放段落

So, although the 1st choice pays 5.4% interest, it is paid only  once per year. The 2nd choice pays 5.3% interest, but pays 365 times per year. The effect of repeatedly paying interest on interest is the compounding of the interest. Clearly, the investor is benefitted by more frequent compounding.  
::因此,尽管第一选择支付5.4%的利息,但每年只支付一次。 第二选择支付5.3%的利息,但每年支付365次。 反复支付利息对利息的影响是利息的增益。 显然,投资者因更频繁的增益而受益。

播放段落

Example 5
::例5

播放段落

Compare the values of the investments shown in the table.  H ow does the compounding influence the value of the investment?
::比较表中显示的投资价值。复合对投资价值有何影响?

	Principal	r	n	t
a.	$4,000	.05	1 (annual)	8
b.	$4,000	.05	4 (quarterly)	8
c.	$4,000	.05	12 (monthly)	8
d.	$4,000	.05	365 (daily)	8
e.	$4,000	.05	8,760 (hourly)	8

播放段落

Solution:
::解决方案 :

播放段落

Apply  the compound interest formula. For this example, the $\begin{align*}n\end{align*}$  is the quantity that changes: $\begin{align*}A(8) = 4,\!000 \left (1 + \frac{.05} {n}\right )^{8n}\end{align*}$ .
::应用复利公式。 对于此示例, n 是更改的数量 : A( 8) = 4,000 ( 1+. 05n) 8n 。

	Principal	r	n	t	A
a.	$4,000	.05	1 (annual)	8	$5,909.82
b.	$4,000	.05	4 (quarterly)	8	$5,952.52
c.	$4,000	.05	12 (monthly)	8	$5,962.34
d.	$4,000	.05	365 (daily)	8	$5,967.14
e.	$4,000	.05	8,760 (hourly)	8	$5,967.29

播放段落

A graph of the function $\begin{align*}f(x) = 4,\!000 \left (1 + \frac{.05} {x}\right )^{8x}\end{align*}$ , where  $\begin{align*}x\end{align*}$  represents the number of compounding periods is shown below. The graph indicates that the function has a horizontal asymptote at approximately $5,968.
::函数 f( x) = 4,000 ( 1+. 05x) 8x 的图形显示如下: x 表示复合期数。 该图显示该函数的水平同位数大约为 5,968 美元。

 

播放段落

This means that for the investment of $4,000, at 5% interest for 8 years, compounding more and more frequently will never result in more than about $5,968.
::这意味着,对于4 000美元的投资,8年的利息为5%,增加的频率越来越频繁,将永远不会超过5 968美元。

播放段落

Example 6  
::例6

播放段落

Determine the value of each investment:
::确定每项投资的价值:

播放段落

a) $5,000 is invested in an account that pays 6% interest, compounded monthly. What is the value of the investment after 10 years?
:a) 5 000美元投资在一个每月支付6%利息(复计)的账户中。 10年后的投资价值是多少?

播放段落

Solution:
::解决方案 :

播放段落

$5,000, invested for 10 years at 6% interest, compounded monthly.

$$\begin{align*}A(10) &= 5,\!000 \left (1 + \frac{.06} {12}\right )^{12\cdot 10}\\ A(10) &= 5,\!000 \left (1.005\right )^{120} \\ A(10) &= \$ 9,\!096.98\end{align*}$$
::5 000美元,投资10年,利息6%,每月复数A(10)=5 000(1+.0612)1210A(10)=5 000(1.005)120A(10)=9 096.98美元

播放段落

Thus, the initial $5,000 investment is worth $9,096.98 after 10 years.


::因此,最初的5 000美元投资在10年后价值9 096.98美元。

播放段落

b) $6,000 is invested in an account that pays 2.5% interest, compounded quarterly. What is the value of the investment after 10 years?
:b) 6 000美元投资在一个支付2.5%利息的账户中,每季付2.5%的利息。

播放段落

Solution:
::解决方案 :

播放段落

$6,000, invested for 10 years at 2.5% interest, compounded quarterly.
::6000美元,投资10年,利息2.5%,每季度一次。

播放段落

Quarterly compounding means that interest is compounded 4 times per year. So, in the equation , $\begin{align*}n=4\end{align*}$ .

$$\begin{align*}A(10) &= 6,\!000 \left( 1 + \frac{.025} {4}\right )^{4 \cdot 10} \\ A(10) &= 6,\!000 (1.00625)^{40}\\ A(10) &= \$7,698.16\end{align*}$$
::季度复利意味着利息每年复利4次。在方程式中,n=4.A(10)=6,000(1+.025444}410A(10)=6,000(1.00625)40A(10)=7,698.16美元。

播放段落

Thus, the initial $6,000 investment is worth $7,698.16 after 10 years.


::因此,最初的6 000美元投资在十年后价值7 698.16美元。

播放段落

Example 7
::例7

播放段落

How long does it take for a $2,000 investment, which earns 5% interest compounded continuously to grow to $25,000?
::2 000美元的投资需要多长时间才能赚到5%的利息,再到25 000美元,利息又不断增长到25 000美元?

播放段落

Solution:  
::解决方案 :

播放段落

$$\begin{align*}25,000 &= 2,\!000{e}^{0.05t} \\ 12.5 &= {e}^{0.05t}\\ \ln 12.5 &= \ln \left( {e}^{0.05t}\right) \\ \ln 12.5 &= 0.05t \\ t &= \frac{\ln 12.5}{0.05} \approx 50.5\end{align*}$$
::255=2 000e0.05t12.5=e0.05tn12.5=ln(e0.05t) 12.5=0.05tt=ln12.50.0550.5

播放段落

Thus, it takes approximately 50.5 y ears for the investment of $2,000 to be worth $25,000.
::因此,投资2 000美元大约需要50.5年,价值25 000美元。

播放段落

Summary
::摘要

播放段落
• Compound interest formula:  $\begin{align*}A(t) = p \cdot \left(1 +\frac{r}{n}\right)^{nt}\end{align*}$  
  ::复方利益公式: A( t) =p( 1+rn)
播放段落
• Continuously compounded interest:  $\begin{align*}A(t) = p \cdot {e}^{rt}\end{align*}$   
  ::连续复利: A( t) = pert

播放段落

Review
::回顾

播放段落
1. What is the formula for determining the value of an investment with  compound interest?
   ::确定具有复合利息的投资价值的公式是什么?
播放段落
2. If someone invested $4,500, how much would the person have earned after 4 years at a compounded quarterly interest rate of 2%?
   ::如果有人投资了4500美元,那么4年后以2%的复合季度利率挣了多少钱?
播放段落
3. Kyle opened up a savings account in July. He deposited $900. The bank pays a compounded monthly  interest rate of 5% annually. What is Kyle's balance at the end of 4 years?
   ::Kyle在7月开了一个储蓄账户,他存了900美元。银行每月支付5%的复合利率。四年结束时Kyle的余额是多少?
播放段落
4. After having an account for 6 years, how much money does Roberta have in the account if her original deposit was $11,000, and her semiannually (twice a year)  compound interest rate  is 8.4%?
   ::在拥有6年的账户之后,如果Roberta的原始存款为11 000美元,而且她半年一次(一年两次)的复合利率为8.4%,那么罗贝塔在账户中有多少钱?
播放段落
5. Tom called his bank today to check on his savings account balance. He was surprised to learn that he has balance of $6,600. He opened his account 8 years old with  $5,000, and his interest is compounded monthly. Based on this data, what percent interest rate has the bank been paying on the account?
   ::汤姆今天打电话给他的银行查看他的储蓄账户余额。他惊讶地得知他的存款余额为6 600美元。他用5 000美元开户,8岁开户,每月利息加起来。 根据这个数据,银行在账户上支付的利率是多少?
播放段落
6. Julie opened a 4% interest account with a bank that compounds the interest quarterly. If she deposited $3,000 into the account at the beginning of the year, how much could she expect to have at the end of the year?
   ::朱莉在一家银行开了一个4%的利息账户,该银行每季增加利息。 如果她在年初将3000美元存入该账户,那么她预计年底能拿到多少?
播放段落
7. What is the balance on a deposit of $818, earning 5% interest compounded semiannually (twice a year) for 5 years?
   ::818美元存款的余额是多少,每半年(一年两次)每5年赚取5%的利息(每5年两次)?
播放段落
8. Karen made a decent investment. After 4 years she had $3,250 in her account, and expects to have $16,250 after another 4 years with no additional deposit. Her savings account is a compounding interest account. How much was her original deposit?
   ::凯伦做了一个体面的投资。四年后,她有3,250美元入户,预计四年后会有16,250美元,没有额外的存款。她的储蓄账户是一个复利账户。她的原始存款是多少?
播放段落
9. Write an expression that correctly represents the balance on an account after 7 years, if the account was compounded yearly at a rate of 5%, with an initial balance of $1,000.
   ::写一个表达式,正确代表一个账户7年后的余额,如果该账户每年以5%的费率复算,初始余额为1 000美元。
播放段落
10. Kathy receives an inheritance check for $3,000 and decides to put it in a savings account so she can send her daughter to college when she gets older. Kathy finds an account that pays compounding interest annually at a rate of 14%. The balance on the account can be represented by a function, where $\begin{align*}x\end{align*}$  is the time in years. Write a function, and then use it to determine how much money will be in the account at the end of 7 years.
    ::Kathy收到3000美元的继承支票,并决定将支票存入储蓄账户,以便当女儿长大后,她可以送她上大学。Kathy找到一个每年以14%的利率支付加息的账户。账户上的余额可以用一个函数来表示,X是年中的时间。写一个函数,然后用它来确定在7年结束时,账户里有多少钱。
播放段落
11. Stan is late on his car payment. The finance company charges 3% interest per month it is late. His monthly payment is $300. What is the total amount he will owe if he pays the August 1 bill on October 1? (Assume he paid his September bill on time.)
    ::Stan的汽车付款迟了。 金融公司每月收取3%的利息。 他每月的付款为300美元。 如果他在10月1日支付8月1日的账单,他将拖欠的总额是多少? (假设他按时支付了他的9月账单。 )

播放段落

Today, you get your 1st credit card. It charges 12.49% interest on all purchases, and compounds that interest monthly. Within one day you max out the credit limit of $1,200.
::今天,你得到第一张信用卡。它收取所有购买的12.49%的利息,并每月增加利息。在一天之内,你将最多不超过1 200美元的信用限额。

播放段落
12. If you pay the monthly accrued interest plus $50 towards the initial $1,200 amount every month, how much will you still owe at the end of the 1st 12 months?
    ::如果你每月向最初的1 200美元支付每月累计利息加50美元,那么在12个月后,你还欠了多少钱?
播放段落
13. How much will you have paid in total at the end of the year?
    ::到年底你总共要付多少钱?

播放段落

You are preparing for retirement. You invest $10,000 for 5 years in an account that compounds monthly at 12% per year. However, unless this money is in an IRA or other tax-free vehicle with zero inflation, you also have an annual tax payment of 30% on the earned interest.
::您正在准备退休。 您在每月12 % 的账户中投资了 10,000 美元, 为期5 年。 但是, 除非这笔钱在爱尔兰共和军或其他零通胀免税的车辆中, 否则您每年还得按所得利息缴纳30%的税款。

播放段落
14. How much will you have in 5 years?
    ::5年后你还要多少钱?
播放段落
15. Now, take into account that the money loses 3% spending value per year due to inflation. How much is what you have saved really worth at the end of the 5 years?
    ::现在,考虑到由于通货膨胀,这笔钱每年损失3%的支出价值。 在五年结束时,你所节省的钱到底值多少?

播放段落

Review ( Answers)
::回顾(答复)

播放段落

Please see the Appendix.
::请参看附录。