Sines法律
章节大纲
-
Introduction
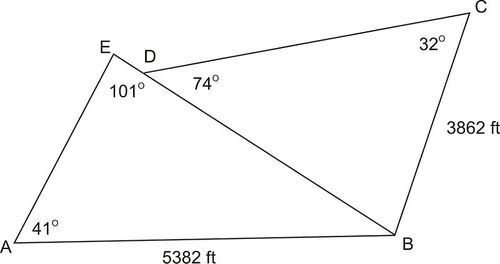
::导言A business group wants to build a golf course on a plot of land that was once a farm. The deed to the land is old, and information about the land is incomplete. If is 5,382 feet, is 3,862 feet, is is is , and is , what are the lengths of the sides of each triangular piece of land?The , which is a generalization of the for any triangle, can be used when:
::对于任何三角形来说,它是该三角形的概括,可用于下列情况:-
Two sides of a triangle and the included angle are known (SAS), or
::三角形两侧和所包括角度为已知(SAS),或 -
All three sides of the triangle are known (SSS).
::三角形的所有三边都是已知的(SSS)。
If the triangle doesn’t fit either of those scenarios, the Law of Sines may apply.
::如果三角形不符合上述两种情况, 可以适用Sines法则。The Law of Sines is a statement about the relationship between the sides and the angles in any triangle. While the Law of Sines will yield one correct answer in many situations, there are times when it is ambiguous , meaning it can produce more than one answer, or no answer.
::《辛那斯定律》是一份关于两边关系和任何三角形角度的声明。 尽管辛那斯定律在许多情况下将产生一个正确的答案,但有时它模棱两可,意思是它可以产生一个以上的答案,或者没有答案。Use the Law of Sines when:
::在下列情况下使用Sines法:-
Two angles and a non-included side are known (AAS), or
::已知两个角度和一个未包含的侧面(AAS),或 -
Two angles and the included side (ASA) are known.
::已知的两个角度和包括的侧面(ASA)是已知的。
When solving a triangle where two sides and the non-included side are known (SSA), this case is known as the Ambiguous Case of the Law of Sines.
::当解决已知两边和未包括一方的三角形时,本案被称为 " 辛尼定律的模糊案例 " 。Derivation of the Law of Sines
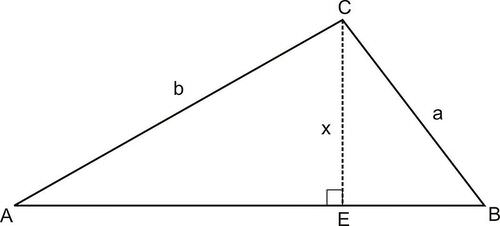
::Sines法的衍生contains altitude , which extends from and intersects . Refer to the length of altitude as .
::ABC 包含从C和AB相交的高度CE。First, and , by the definition of sine. Equivalently,
::首先,罪A=xb 和罪B=xa,根据"正弦"的定义。
:sinA) =xanda(sinB) =xb(sinA) =a(sinB) sinAa=sinBb 或asinA=bsinB
Extending these ratios to angle and side , the Law of Sines is developed.
::将这些比率扩大到角度C和角度c,制定了Sines法。Law of Sines
::Sines法律
Note: Use any two of the three ratios from either form when solving.
::表格1:sinAa=sinBb=sinCcForm 2:asinA=bsinB=csinC 注:在解析时,使用两种形式中的任何两种比率。AAS (Angle-Angle-Side) Case
::AAS( 角度- 角度- 侧) 大小写Example 1
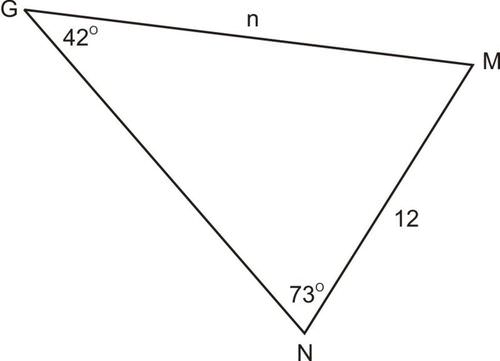
::例1For , and . Find .
::GMN,GG=42,N=73和G=12。Solution:
::解决方案 :Two angles and one non-included side are known. The other non-included side "> can be found.
::已知两个角度和一个未包含的侧面(g),可找到另一个未包含的侧面。
::12sin\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\1715。Example 2
::例2From the diagram in Example 1, find and .
::从例1中的图表中找到 M 和 m。Solution:
::解决方案 :is simply . To find side , use either the Law of Sines or Law of Cosines. Using the Law of Sines :
::M只是180427365。Option 1: and
::备选1:++G和g
::{\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}为什么? {\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}为什么? {\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}为什么? {\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}为什么?Option 2: and
::备选2:N和n
::1715 msin 73 73 1715 msin 73 *1715 sin 65 m=1715 msin *65 75 @sin 73 @m_16.25Example 3
::例3Recall the problem from the Introduction. A business group wants to build a golf course on a plot of land that was once a farm. If is 5,382 feet, is 3,862 feet, is is is , and is , what are the lengths of the sides of each triangular piece of land?
::回顾导言中的问题。一个商业团体想在曾经是农场的一块土地上建造高尔夫球场。如果AB是5,382英尺,BC是3,862英尺,ZAEB是101,BDC是74,EAB是41,DCB是32,那么每块三角地的两边长度是多少?Solution:
::解决方案 :Use the Law of Sines to determine the length of side .
::使用Sines法来确定EB的长度。
::101 5 382EBsin 101 5 382EBsin 101 5 382sin 41EB= 5 382sin 41 asin 101 EB_3 597英尺Use the Law of Sines to determine the length of side .
::使用Sines法来确定DB侧的长度。
::DB=3,862sin\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\3,862sin\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\2,129129英尺。To find the length of , start by finding . Then use the Law of Sines.
::找到 AE 的长度, 首先找到 QABE=180- (41+101) = 38 。 然后使用 Sines 法则 。
To solve for the last side, find the angle: . Since there are two equal angles, there will be two equal sides and .
::5382sin101AAEsin3838385382sin101AEAE=3 375.5英尺 最后一边的解答角为 7<9,9sin51.067.00024. 由于两个角度相等, 双面相等, DC=BC=3,862英尺。ASA (Angle-Side-Angle) Case
::ASA( 闪光- 闪光- 闪光) 案例The 2nd case to use the Law of Sines is when two angles in a triangle and the included side are known (ASA). For instance, in :
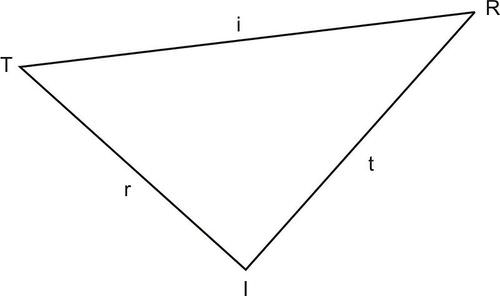
::使用Sines定律的第2个案例是已知三角形和包括的侧面的两个角度(ASA)。, and are known.
::T、R和我都已经知道了,and are known.
::T,i,r是已知的。, and are known.
::R,I,和t是已知的。Example 4
::例4In the picture above, , and . Find the measure of .
::在以上图片中,请找到 t 的度量 。Solution:
::解决方案 :Since two angles and the included side are known, you can find either of the non-included sides using the Law of Sines. Start by finding the 3rd angle using the fact that the sum of all of the angles in a triangle must equal .
::由于已知两个角度和包含的侧面, 您可以使用“ 辛那斯定律” 找到一个未包含的侧面。 从找到第三个角度开始, 使用三角形中所有角度的总和必须等于 180\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\
::*I=180 -(83+24)... *I=180 -107 *I=73*Now u se the Law of Sines to find :
::现在使用Sines法则来寻找 t:
::-==YTET -伊甸园字幕组= -伊甸园字幕组= -伊甸园字幕组= -伊甸园字幕组= -伊甸园字幕组= -伊甸园字幕组= -伊甸园字幕组= -伊甸园字幕组= -伊甸园字幕组= -伊甸园字幕组= -伊甸园字幕组= -伊甸园字幕组= -伊甸园字幕组= -伊甸园字幕组= -伊甸园字幕组= -伊甸园字幕组= -伊甸园字幕组= -伊甸园字幕组= -伊甸园字幕组=Example 5
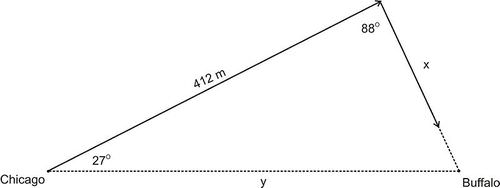
::例5To avoid a snowstorm on a flight from Chicago to Buffalo, the pilot moved off the normal flight path. After flying 412 miles in this direction, the pilot turned the plane back toward Buffalo. The angle formed by the 1st flight course and the 2nd flight course is . For the pilot, two issues are pressing:
::为了避免从芝加哥飞往水牛城的航班发生暴风雪,飞行员将27从正常飞行路线上移出。在朝这个方向飞行412英里后,飞行员将飞机转回水牛城。第一飞行路线和第二飞行路线所形成的角度是88。对于飞行员来说,有两个问题很紧迫:-
What is the total distance of the modified flight path?
::修改后的飞行路径的总距离是多少? -
How much farther did the plane travel than if he had chosen the original course?
::飞机飞行的距离比他选择原航程还要远多?
Solution:
::解决方案 :Part 1: In order to find the total distance of the modified flight path, find side . To find side , use the Law of Sines. Since two angles and the included side are known, this is an ASA case.
::第1部分:为了找到修改后的飞行路径的总距离,请找到侧面 x。要找到侧面 x,请使用Sines定律。由于已知两个角度和包括的侧面,这是一个 ASA 案例。
::缺少 Angle= 180 ( 27 ) = 65The total distance of the modified flight path is .
::经修改的飞行路径总距离为412+206.4=618.4米。Part 2: To find how much farther the pilot had to travel, find , the original flight path. Use the Law of Sines again to find .
::第2部分:为了找到飞行员必须走多远, 找到y, 最初的飞行路径。 再次使用Sines法则来找到y 。
::Siney(sin65)=412(sin88)Cross乘以.y=412(sin88)sin=6565*DivideJohn had to travel farther.
::约翰不得不远行618.4-454.3=164.1米。SSA ( Side- Side-Angle) Case
::SSS( 半半半半半半角) 案例In geometry, two sides and a non-included angle do not necessarily define a unique triangle. Consider the following cases given , and :
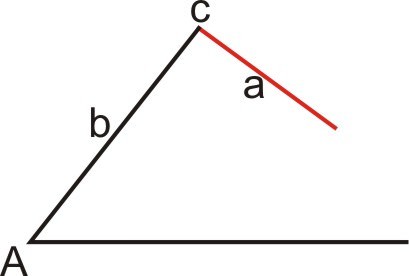
::在几何学中,两边和未包含角度不一定定义一个独特的三角形。Case 1: No triangle exists
::案件1:不存在三角关系(a <b)In this case, and side is too short to reach the base of the triangle. Since no triangle exists, there is no solution.
::在此情况下, < b 和 侧面 a 的长度太短, 无法到达三角形的底部 。 由于不存在三角形, 因此没有解决方案 。Case 2: One triangle exists
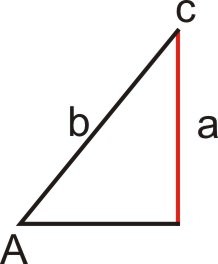
::案例2:存在一个三角形(a<b)In this case, and side is perpendicular to the base of the triangle. Since this situation yields exactly one triangle, there is exactly one solution.
::在此情况下, <b 和 侧面 a 与三角形底部垂直。 由于此情况产生一个三角形, 完全只有一个解决方案 。Case 3: Two triangles exist
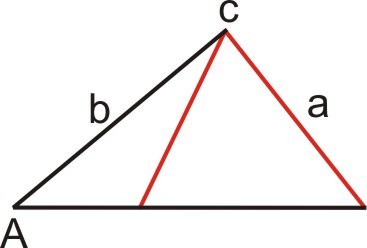
::案例3:存在两个三角形(a < (b))In this case, and side meets the base at exactly two points. Since two triangles exist, there are two solutions. Note that only the angle opposite the longest side of a triangle may be obtuse. To eliminate the need for considering two possible outcomes, a void using the Law of Sines to determine the largest angle of a triangle.
::在此情况下, a < b 和 a 的侧面会在精确的两个点上满足基点 。 由于存在两个三角, 有两个解决方案 。 请注意, 只有三角形最长的侧面对面的角可能会被忽略 。 要消除考虑两个可能的结果的必要性, 避免使用 Sines 定律来确定三角形的最大角 。Case 4: One triangle exists
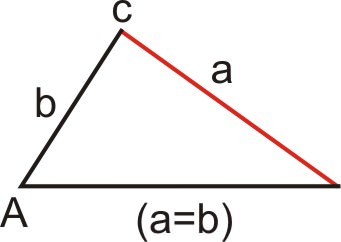
::案例4:存在一个三角形(a=b)In this case, and side meets the base at exactly one point. Since there is exactly one triangle, there is one solution.
::在此情况下, a=b 和 a 侧相匹配, 恰好在一个点与基点相匹配。 因为完全只有一个三角形, 只有一个解决方案 。Case 5: One triangle exists
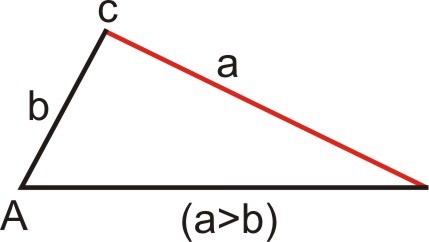
::案例5:存在一个三角形(a>b)In this case, and side meets the base at exactly one point. Since there is exactly one triangle, there is one solution.
::在此情况下, a> b 和 侧面与基点完全匹配一个点。 由于完全只有一个三角形, 只有一个解决方案 。Case 3 is referred to as the Ambiguous Case because there are two possible triangles and two possible solutions. One way to check to see how many possible solutions (if any) a triangle will have is to compare sides and . In the situation, where , determine how many solutions there will be by analyzing and .
::案例3被称为“模糊案例”,因为有两种可能的三角形和两种可能的解决方案。一种是比较a和b两边,以检查三角形有多少可能的解决方案(如果有的话)。在这种情况下, <b,通过分析a和bsinA来确定有多少解决方案。If: Then: i. No solution, one solution, two solutions a. No solution b. One solution c. Two solutions ii. One solution iii. One solution Example 6
::例6Determine if the sides and angle given determine zero, one, or two triangles. All sets contain an angle, its opposite side, and the side between them.
::确定给定的边和角度是否确定 0、 1 或两个三角形。 全部集合都包含一个角度、 其对面和它们之间的侧面 。a.
::a. a=5,b=8,A=62.19Solution:
::解决方案 :Even though , and are not used in every example, follow the same pattern from the table by multiplying the non-opposite side (of the angle) by the sine of the angle.
::即使并非每个例子都使用 a、b 和 A, 仍遵循表格中的相同模式, 将非对面面面( 角度) 乘以角的正弦 。. Since , there is no solution.
::5 < 8,8sin62.197.076. 由于5<7.076,没有解决办法。b.
::b. c=14,b=10,B=15.45Solution:
::解决方案 :. Since , there are two solutions.
::10<14,14sin15.453.73。自10>3.73以来,有两种解决办法。c.
::d=16,g=11,D=44,94Solution:
::解决方案 :, so there is one solution.
::16>11,所以只有一个解决办法。d.
::a=9,b=7,B=51.06Solution:
::解决方案 :. Since , there is no solution.
::7<9,9sin51.067.00024。自7<7.00024以来,没有解决办法。Example 7
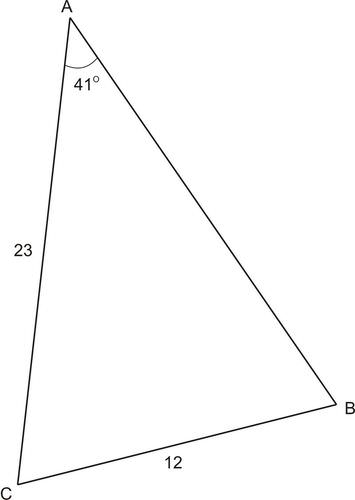
::例7Find .
::找找BSolution:
::解决方案 :Use the Law of Sines to determine the angle.
::使用Sines法则来确定角度。
::-=YTET -伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=- 翻译:Since no angle exists with a sine greater than 1, there is no solution to this problem.
::由于没有任何角度存在超过1的必备条件,因此这个问题没有解决办法。Similarly, the 1st step could have compared and before proceeding to see how many solutions were possible.
::同样,第一个步骤本来可以比较a和bsinA,然后才着手研究有多少解决办法是可能的。: since , there are no solutions.
::a=12,bsinA=15.1:自12<15.1和a<bsinA以来,没有解决办法。Example 8
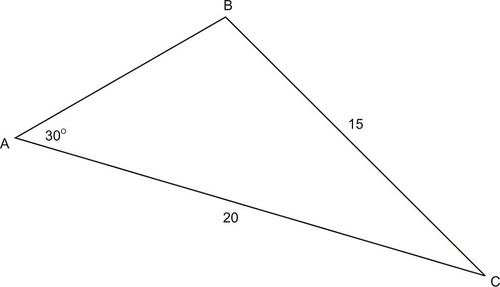
::例8In triangle , and . Find .
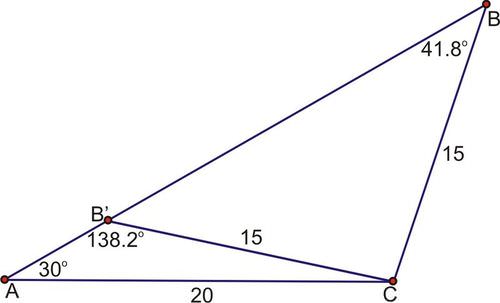
::在三角形ABC, a=15, b=20, 和A=30。 查找 B 。Solution:
::解决方案 :Again in this case, and two sides and a non-included angle are known. By comparing and , . Since there will be two solutions to this problem.
::在此情况下,可以知道一个 <b和两面以及一个未包含的角度。通过比较一个和bsina, a=15,bsinA=10。由于15>10,这个问题将有两个解决办法。
::B2020sin 30_B15_B20sin_B20sin_30_B20sin_30_B30_15_sin_B066666_B_B_B=41.8_BHowever, there are two angles less than with a sine of 0.6666667. The 1st one is , which was found by using the inverse sine function. To find the 2nd one, subtract this 1st solution from .
::然而,有两个小于180的角,正弦值为0.666667。第一个角是41.8,它是用正弦值的反函数找到的。要找到第二个角,请从180\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\To check to make sure is a solution, use the Triangle Sum Theorem to find the 3rd angle. All three angles must add up to .
::要检查确定138.2是否是一个解决方案, 请使用三角 Sum 理论查找第三个角度。 所有三个角度必须加到 180 。
::{\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}... {\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}... {\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}... {\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}... {\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}Since both solutions yield a valid 3rd angle with measure between this problem yields two solutions. Either or .
::由于两种解决方案都产生有效的第三种角度, 度量介于0180之间, 这个问题产生两种解决方案, 要么是B=41.8, 要么是138.2。Summary
::摘要-
Law of Sines:
::辛烷定律:表1: 罪.Aa=sin_Bb=sin_Cform2:asin_A=bsin_B=csin_C -
The Ambiguous Case (SSA): Either zero, one, or two triangles result.
::模糊情况(SSA):要么零,要么一,要么两个三角结果。If: Then: i. No solution, one solution, two solutions a. No solution b. One solution c. Two solutions ii. One solution iii. One solution
::模糊的大小写( SSA) : 要么0, 1, 要么两个三角形结果 。 如果 : 之后 : i. a < b no 解决方案, 一个解决方案, 两个解决方案 a. a. a. a. a. a. a. a. a. a. a. a. a. a. a. b. 一个解决方案
Review
::回顾Find all possible measures of angle if any exist for each of the following triangle values.
::如果对以下三角值中的每一值都存在,请查找角B的所有可能的度量。-
::A=30,a=13,b=15 -
::A=42,a=21,b=12 -
::A=22,a=36,b=37 -
::A=87,a=14,b=12 -
::A=31,a=25,b=44 -
::A=59,a=37,b=41 -
::A=81,a=22,b=20 -
::A=95,a=31,b=34 -
::A=112,a=12,b=15 -
::A=78,a=20,b=16 -
In
, a=10 and
What's a possible value for b that would produce two triangles?
::在“ABC”中, a=10 和 mB=39\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\B\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\ -
In
, a=15 and
What's a possible value for b that would produce no triangles?
::在 ABC 中, a= 15 和 mB= 67\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\ xB\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\B\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\BBBBBBB -
In
, a=21 and
What's a possible value for b that would produce one triangle?
::在 ABC 中, a= 21 和 mB= 99\\\\\\\\\\\\\\\\\\\\\\\\可以产生一个三角形的 b 值是多少? -
Bill and Connie are each leaving for school. Connie's house is 4 miles due east of Bill's house. Bill can see the school in the direction
east of north. Connie can see the school on a line
west of north. What is the straight line distance of each person from the school?
::比尔和康妮都要去上学 康妮的房子在比尔房子东面4英里处 -
Rochelle and Rose are each looking at a hot air balloon. They are standing 2 miles apart. The angle of elevation (meaning the angle from the ground up to the balloon in this case) for Rochelle is
and the angle of elevation for Rose is
. How high off the ground is the balloon?
::Rochelle和Rose各自在看热气球,它们相距两英里。Rochelle的高度角度(即从地面到气球的角度)是30°C,而Rose的高度角度是34°C。气球离地面多高?
Answers for Review Problems
::回顾问题的答复Please see the Appendix.
::请参看附录。 -
Two sides of a triangle and the included angle are known (SAS), or