Section: 三角数等量 | 8.6 三角等量法

Section outline

Introduction
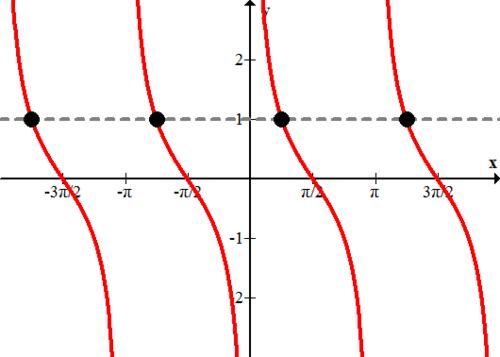
::导言

A temporary employment agency manager gathered data on the number of movers needed during one year by local moving companies. The manager developed the model
::一名临时就业机构经理收集了一年来当地流动公司所需搬运工人数的数据。

$\begin{aligned} N (t) = 20 + 4 \sin (2 t), t \geq 0 . \end{aligned}$ The graph of the function is:
::N( t) = 20+4sin( 2t) t0。函数的图形为 :

The manager needs to know the months during which 20 movers are needed. In the first 12 months, this happens several times. The equation to be solved is
::经理需要知道需要20个搬运工的月份。在头12个月中,这种情况会发生几次。要解决的公式是:

$\begin{aligned} 20 = 20 + 4 \sin (2 t) . \end{aligned}$

::20=20+4sin(2吨)。

Solving this trigonometric equation is similar to solving a polynomial, rational, exponential, or logarithmic equation. Factoring and other algebraic techniques are used to isolate the variable . The biggest difference with trigonometric equations is the opportunity for an infinite number of solutions that must be described with a pattern. The equation $\begin{aligned} \cos x = 1 \end{aligned}$ has many solutions, including 0 and $\begin{aligned} 2 π \end{aligned}$ . How can they all be described?
::解决这个三角方程式与解决多数值、理性、指数或对数方程式相似。乘法和其他代数法用来分离变量。三角方程式的最大差异是有机会找到无限数的解决方案, 且必须用一个模式来描述。方程式 osx=1 有许多解决方案, 包括 0 和 2。如何描述它们?

How to Solve a Trigonometric Equation
::如何解决三角等同

Solve for the variable as you would a linear equation.
::以线性方程的方式解决变量。

Use inverse trigonometric functions to isolate the variable.
::使用逆三角函数分隔变量。

Use Pythagorean Trigonometric, sum and difference, and other trigonometric identities to get a single trigonometric function , such as sine or cosine.
::使用 Pythagoren Trigonorian 测量、总和和差异,以及其他三角特征来获得单一的三角函数,如正弦或共弦。

Use sum and difference, double angle, and half angle identities to get a single angle.
::使用和差异, 双角度, 和半角度身份来获得一个角度。

Use algebraic techniques, such as factoring or squaring, to further simplify the expressions.
::使用代数技术,如乘数或方位法,进一步简化表达式。

Use the unit circle to find the initial solution or to determine values within the specified interval. There may be more than one value.
::使用单位圆查找初始解决方案或确定指定间隔内的值。可能有一个以上的值。

Provide an appropriate set of solutions.
::提供一套适当的解决办法。

When you solve an equation, the equation is an identity if the two sides of the equation are always equal, such as $\begin{aligned} π = π \end{aligned}$ . The equation has no solution if the two sides of an equation are never equal, such as $\begin{aligned} \sin x = 3 \end{aligned}$ .
::当您解析一个方程式时,如果方程式的两面总是相等, 方程式就是一个身份, 例如。如果方程式的两面从不相等, 方程式就没有解答, 例如 sinx=3 。

The following video provides examples of solving trigonometric equations that are factorable or in quadratic form:
::以下视频提供了可计数或四方形的三角方程解答实例:



The following video provides examples of solving trigonometric equations that require the use of identities, are not factorable, or need to be squared to solve:
::以下视频提供了解决三角方程式的例子,这些方程式需要使用身份、不可计算或需要平方以解决:

Examples
::实例

Example 1
::例1

Solve the following equation algebraically and confirm graphically on the interval $\begin{aligned} [- 2 π, 2 π] \end{aligned}$ :
::以代数方式解决以下方程式,并在间隔处用图形确认[-2-2],2]:

$\begin{aligned} \cos 2 x = \sin x . \end{aligned}$

::2x=sinxx。。。

Solution:
::解决方案 :

Step 1: Use the double angle identity to get a single trigonometric function instead of a mixture of functions. Then use algebraic techniques to further simplify.
::第1步:使用双角特性来取得单一三角函数,而不是组合函数。然后使用代数技术进一步简化。

$\begin{aligned} \cos 2 x & = \sin x \\ 1 - 2 \sin^{2} x & = \sin x \\ 0 & = 2 \sin^{2} x + \sin x - 1 \\ 0 & = (2 \sin x - 1) (\sin x + 1) \end{aligned}$

::COs2x=sinx1-2sin2}2x=sinx0=2sin2}x+sinx-10=(2sinx-1)(sinx+1)

Step 2: Set the two factors equal to 0. Use the unit circle to determine values within the specified interval.
::第2步:设定等于 0 的两个系数。使用单位圆来确定指定间隔内的值。

$\begin{aligned} 0 & = 2 \sin x - 1 \\ \frac{1}{2} & = \sin x \\ x & = \frac{π}{6}, \frac{5 π}{6} \end{aligned}$

::0=2sinx-112=sinxxxxxxxx6,56

The for these angles are $\begin{aligned} - \frac{11 π}{6} and - \frac{7 π}{6} . \end{aligned}$
::这些角度是-111-6和-7-6。

$\begin{aligned} 0 & = \sin x + 1 \\ - 1 & = \sin x \\ x & = - \frac{π}{2}, \frac{3 π}{2} \end{aligned}$

::0=sinx+1-1=sinxxxxxxx2,32

Step 3: These are the six solutions to the initial equation in the given interval. The solutions appear as intersection points for the two graphs $\begin{aligned} f (x) = \cos 2 x \end{aligned}$ (in red and intersecting the $\begin{aligned} y \end{aligned}$ -axis at 1) and $\begin{aligned} g (x) = \sin x \end{aligned}$ (in blue and intersecting the origin).
::步骤 3 : 这些是给定间隔内初始方程式的六个解决方案。解决方案显示为两个图形 f( x) = cos% 2x( 红色和 y 轴在 1 时交叉) 和 g( x) = sinx( 蓝色和源交叉) 的交叉点。

Example 2
::例2

Determine the general solution to the following equation:
::确定下列等式的一般解决办法:

$\begin{aligned} \cot x - 1 = 0. \end{aligned}$

::COTx -1=0。

Solution:
::解决方案 :

Step 1: Solve for the variable as you would a linear equation.
::步骤 1: 以线性方程的方式解决变量。

$\begin{aligned} \cot x - 1 & = 0 \\ \cot x & = 1 \end{aligned}$

::comtx- 1 = 0ctx= 1

Step 2: Use the unit circle to find the initial solution. One solution is $\begin{aligned} x = \frac{π}{4} \end{aligned}$ .
::第2步:使用单位圆找到初始解决方案。一个解决方案是 x4 。

Step 3: However, since this question asks for the general solution, find every possible solution. The cotangent has a period of $\begin{aligned} π, \end{aligned}$ which means if $\begin{aligned} π \end{aligned}$ is added or subtracted from $\begin{aligned} \frac{π}{4}, \end{aligned}$ then
$\begin{aligned} x = \frac{π}{4} + n \cdot π \end{aligned}$
will also yield a height of 1. To capture all these other possible $\begin{aligned} x \end{aligned}$ values, use this notation:
::步骤3:然而,由于这一问题要求通用解决方案,请找到所有可能的解决方案。余切期为________________________,这意味着如果增加或减去_____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________。

$\begin{aligned} x = \frac{π}{4} + n \cdot π, \end{aligned}$ where $\begin{aligned} n \end{aligned}$ is a integer.
::x4+n, n 是整数。

Example 3
::例3

Solve the following equation:
::解决以下方程式:

$\begin{aligned} 4 \cos^{2} x - 1 = 3 - 4 \sin^{2} x . \end{aligned}$

::4cos2x -1=3 -4sin2x。

Solution:
::解决方案 :

Use algebraic techniques to simplify. Then use a Pythagorean Trigonometric Identity to further simplify.
::使用代数技术来简化。然后使用比达哥里安三角测量特性来进一步简化。

$\begin{aligned} 4 \cos^{2} x - 1 & = 3 - 4 \sin^{2} x \\ 4 \cos^{2} x + 4 \sin^{2} x & = 3 + 1 \\ 4 (\cos^{2} x + \sin^{2} x) & = 4 \\ 4 & = 4 \end{aligned}$

::4cos2%x- 1=3- 4sin2x4cos2x+4sin2x=3+14(cos2x+sin2x)=44=4

This equation is always true, which means the right side is always equal to the left side. This is an identity.
::这个等式总是对的, 这意味着右侧总是等于左侧。这是一个特性。

Example 4
::例4

Return to the problem from the Introduction. During which months over a 12-month interval will there be a demand for 20 movers ?
::回到引言中的问题,在12个月间隔的几个月里,将需要20个搬运工?

$\begin{aligned} 20 = 20 + 4 \sin (2 t), t \in [0, 12] \end{aligned}$
Solution:
Use the unit circle to determine values within the specified interval.
::20=20+4sin(2t),t[0,12] 解答:使用单位圆来确定指定间隔内的值。

$\begin{aligned} 20 & = 20 + 4 \sin (2 t) \\ 0 & = 4 \sin (2 t) \\ 0 & = \sin 2 t \\ 2 t & = 0 + n π, n is an integer \\ t & = \frac{n π}{2}, n is an integer \\ n & = 0, 1, 2, 3, 4, 5, 6, 7 \\ t & \approx 0, 1.57, 3.14, 4.71, 6.28, 7.85, 9.42, 11.00 \end{aligned}$

::20=20+4sin(2t)0=4sin(2t)0=sin2t2t=0+n,n是一个整数=n2,n是一个整数=0,1、2,3,4,5,6,770t0,1.57,3.14,4.71,6.28,7.85,9.42,11.00

The manager can expect that demand for movers in the 1st (month 0), 2nd, 4th, 5th, 7th, 8th, 10th, and 12th months.
::经理可以预计,在第一(月0),第二、第四、第五、第七、第八、第十和第十二个月,对搬运工的需求将会达到。

Example 5
::例5

Solve the following equation on the interval $\begin{aligned} (2 π, 4 π) \end{aligned}$ :
::在间隔(2,4)上解决以下方程式:

$\begin{aligned} 2 \sin x + 1 = 0. \end{aligned}$

::2sinx+1=0。

Solution:
::解决方案 :

Step 1: S olve for the solutions within one period, and then find the solutions in the correct interval.
::步骤1:在一个时期内解决解决方案,然后在正确的间隔内找到解决方案。

$\begin{aligned} 2 \sin x + 1 & = 0 \\ \sin x & = - \frac{1}{2} \\ x & = \frac{7 π}{6}, \frac{11 π}{6} \end{aligned}$

::2sinx+1=0sinx12x=76、116

Step 2: Add $\begin{aligned} 2 π \end{aligned}$ to each of these solutions to get solutions that are in the interval.
::第2步:在每种解决办法中增加2,以获得间隔内的解决办法。

$\begin{aligned} x = \frac{19 π}{6}, \frac{23 π}{6} \end{aligned}$

::x=19%6,23%6

Example 6
::例6

Solve the following equation exactly:
::准确解决以下方程式:

$\begin{aligned} 2 \cos^{2} x + 3 \cos x - 2 = 0. \end{aligned}$

::2cos2x+3cosx-2=0。

Solution:
::解决方案 :

Step 1: Start by factoring:
::第1步:通过保理因素开始:

$\begin{aligned} 2 \cos^{2} x + 3 \cos x - 2 & = 0 \\ (2 \cos x - 1) (\cos x + 2) & = 0 \end{aligned}$

::2cos2x+3cosx-2=0(2cos_x-1)(cos_x+2)=0

Step 2: Set the two factors equal to 0. Use the unit circle to determine the initial solutions .
::第2步:将两个系数设为 0。使用单位圆来确定初始解决方案。

$\begin{aligned} 2 \cos x - 1 & = 0 \\ \cos x & = \frac{1}{2} \\ x & = \frac{π}{3}, - \frac{π}{3} \end{aligned}$

::2cosx- 1= 0cosx= 12x3,%3

$\begin{aligned} \cos x + 2 & = 0 \\ \cos x & = - 2 \end{aligned}$

::COsx+2=0cosx2

Since $\begin{aligned} \cos x \neq - 2 \end{aligned}$ , no solutions exist from this factor .
::自Cosx2以来,这一因素没有解决办法。

Step 3: These are the solutions within the interval $\begin{aligned} - π \end{aligned}$ to $\begin{aligned} π \end{aligned}$ . Since this represents one full period of cosine, the rest of the solutions are just multiples of $\begin{aligned} 2 π \end{aligned}$ added and subtracted to these two values.
::步骤3:这些是 \\ \ 至 \ 的间隔内的解决办法。由于这代表一个完整的余弦期, 其余的解决方案只是2 +++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++

$\begin{aligned} x = \pm \frac{π}{3} + n \cdot 2 π, where n is an integer \end{aligned}$

::x3+n%2, n 是整数

Example 7
::例7

Create an equation that includes the solutions $\begin{aligned} \frac{π}{4} + n \cdot 2 π, \end{aligned}$ where $\begin{aligned} n \end{aligned}$ is an integer.
::创建包含解决方案%4+n%2的方程式, n是整数。

Solution:
::解决方案 :

There are an infinite number of possible equations that will work.
::有无数可能的方程式可以发挥作用。

If we use the sine function , $\begin{aligned} \sin \frac{π}{4} = \frac{\sqrt{2}}{2}, \end{aligned}$ an option that works is
::如果我们使用正弦函数,sin4=22, 一个有效的选项就是

$\begin{aligned} \sin x = \frac{\sqrt{2}}{2} . \end{aligned}$

Note that this equation also has the solutions $\begin{aligned} \frac{3 π}{4} + n \cdot 2 π \end{aligned}$ .
::sináx=22。请注意, 此方程式也包含 34+n2的解决方案。

Summary
::摘要

To solve a trigonometric equation, simplify algebraically to isolate the variable.
::要解决三角方程,请简化代数以孤立变量。

Use trigonometric identities when possible.
::在可能的情况下使用三角特征。

Use the unit circle to find the initial solution or to determine values within the specified interval.
::使用单位圆查找初始解决方案或确定指定间隔内的值。

Trigonometric equations may have an infinite number of solutions that repeat in a certain pattern because they are periodic functions.
::三角方程式可能有无限数量的解决方案,由于是周期函数,在某种模式中重复使用。

Review
::回顾

Solve each equation on the interval $\begin{aligned} [0, 2 π) \end{aligned}$ .
::在间隔[0,2]中解决每个方程。

1. $\begin{aligned} 3 \cos^{2} \frac{x}{2} = 3 \end{aligned}$
::1. 3cos2x2=3

2. $\begin{aligned} 4 \sin^{2} x = 8 \sin^{2} \frac{x}{2} \end{aligned}$
::2. 4sin2x=8sin2x2

Find approximate solutions to each equation on the interval $\begin{aligned} [0, 2 π) \end{aligned}$ .
::在间距[0,2]为每个方程寻找近似解决办法。

3. $\begin{aligned} 3 \cos^{2} x + 10 \cos x + 2 = 0 \end{aligned}$
::3. 3cos2x+10cosx+2=0

4. $\begin{aligned} \sin^{2} x + 3 \sin x = 5 \end{aligned}$
::4 sin2 x+3sinx=5

5. $\begin{aligned} \tan^{2} x + \tan x = 3 \end{aligned}$
::5. tan2x+tanx=3

6. $\begin{aligned} \cot^{2} x + 5 \tan x + 14 = 0 \end{aligned}$
::6. 科特2x+5tanx+14=0

7. $\begin{aligned} \sin^{2} x + \cos^{2} x = 1 \end{aligned}$
::7.2x+cos2x=1

Solve each equation on the interval $\begin{aligned} [0, 360^{\circ}) \end{aligned}$ .
::在间隔[0,360]中解决每个方程。

8. $\begin{aligned} 2 \sin (x - \frac{π}{2}) = 1 \end{aligned}$
::8. 2sin(x2)=1

9. $\begin{aligned} 4 \cos (x - π) = 4 \end{aligned}$
::9. 4cos(x)=4

Solve each equation on the interval $\begin{aligned} [2 π, 4 π) \end{aligned}$ .
::在间距[2,4]上解决每个方程。

10. $\begin{aligned} \cos^{2} x + 2 \cos x + 1 = 0 \end{aligned}$
::10. cos2x+2cosx+1=0

11. $\begin{aligned} 3 \sin x = 2 \cos^{2} x \end{aligned}$
::11. 3sinx=2cos2xx

12. $\begin{aligned} \tan x \sin^{2} x = \tan x \end{aligned}$
::12, tanxin2, x=tanx

13. $\begin{aligned} \sin^{2} x + 1 = 2 \sin x \end{aligned}$
::13. 2x+1=2sinx

14. $\begin{aligned} \sec^{2} x = 4 \end{aligned}$
::14.2x=4

15. $\begin{aligned} \sin^{2} x - 4 = \cos^{2} x - \cos 2 x - 4 \end{aligned}$
::15.2x-4=cos2x-cos2x-cos2x-4

Review (Answers)
::回顾(答复)

Please see the Appendix.
::请参看附录。

Section outline

Introduction ::导言

How to Solve a Trigonometric Equation ::如何解决三角等同

Examples ::实例

Summary ::摘要

Review ::回顾

Review (Answers) ::回顾(答复)

Introduction
::导言

How to Solve a Trigonometric Equation
::如何解决三角等同

Examples
::实例

Summary
::摘要

Review
::回顾

Review (Answers)
::回顾(答复)