Section: 三个变量中的解决线性系统 | 10.3 三个变量中的解决线性系统

Section outline

Introduction
::导言

You want to make a platter for a summer picnic.
::你想为暑假野餐做盘盘子

Three pounds of squash plus five pounds of green beans plus one pound of melon cost $20. Three pounds of squash plus two pounds of green beans plus two pounds of melon cost $21. Four pounds of squash plus three pounds of green beans plus three pounds of melon cost $30. How much does each fruit cost?
::三磅南瓜加五磅绿豆加一磅瓜 20美元 3磅南瓜加两磅绿豆加两磅西瓜 21美元 4磅南瓜加三磅青豆加三磅西瓜加三磅西瓜 30美元

Linear Systems in Three Variables
::三个变量中的线性系统

An equation in three variables, such as $\begin{aligned} 2 x - 3 y + 4 z = 10 \end{aligned}$ , is an equation of a plane in three dimensions . In other words, this equation expresses the relationship between the three coordinates of each point on a plane. The solution to a system of three equations in three variables is a point in space that satisfies all three equations. When we add a third dimension, we use the variable , $\begin{aligned} z \end{aligned}$ , for the third coordinate. For example, the point (3, -2, 5) would be $\begin{aligned} x = 3, y = - 2, \end{aligned}$ and $\begin{aligned} z = 5 \end{aligned}$ . A solution can be verified by substituting the $\begin{aligned} x, y, \end{aligned}$ and $\begin{aligned} z \end{aligned}$ values into the equations to see if they are valid.
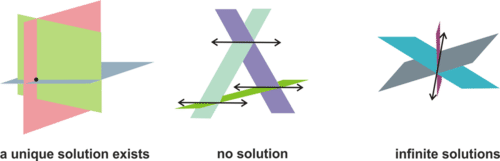
::三个变量中的方程式, 如 2x-3y+4z=10, 是平面的三个维度的方程式。换句话说, 这个方程式表示平面上每个点的三个坐标之间的关系。三个变量中三个方程式的解答是满足所有三个方程式的空间点。当我们添加第三个维度时, 我们使用变量 z, 第三个坐标。例如, 点( 3, 2, 5) 将是 x=3, y2 和 z=5 。一个解决方案可以通过在方程式中替换 x,y 和 z 值来验证它们是否有效。

A system of three equations in three variables consists of three planes in space. These planes could intersect with each other or not as shown in the diagrams below.
::三个变量中的三个方程式系统由三平面组成。这些方程式可以相互交叉,也可以不相互交叉,如下图所示。

In the first diagram, the three planes intersect at a single point. Thus, a unique solution exists and can be found.
::在第一个图表中,三平面在一个点上交叉。因此,有一个独特的解决方案存在,可以找到。

The second diagram illustrates one way that three planes can exist. It is also possible to have three parallel planes. Moreover, there could be two parallel planes and a third plane that intersects them. In all of these cases, there is no point that is in all three planes. Therefore , there are no solutions to these systems.
::第二个图表说明了三架飞机存在的一种方式。 3架平行飞机也有可能存在。此外, 可能还有两架平行飞机和第三架飞机交叉。在所有这些情况下,这三架飞机都没有任何意义。因此, 这些系统没有解决办法。

The third diagram shows three planes intersecting in a line. Every point on this line is a solution to the system. Therefore, the system has infinite solutions.
::第三张图表显示三平面在一行中交叉。这条线上的每一个点都是系统的解决办法。因此,这个系统有无限的解决办法。

Play, Learn, and Explore Intersecting Planes: .
::玩耍、学习和探索相交的平面: .

To solve a system of three variables in three equations, we will be using the elimination method. This time we will take two equations at a time to eliminate one variable. Then we will use the resulting equations in two variables to eliminate a second variable and solve for the third. This process is simply an extension of the linear combination procedure used to solve systems with two equations in two variables.
::为了在三个方程式中解决三个变量的系统, 我们将使用消除方法。这一次我们每次要用两个方程式来消除一个变量。然后我们用两个变量中得出的方程式来消除第二个变量, 然后解决第三个变量。这个过程只是用来解决两个变量中两个方程式的系统的线性组合程序的延伸。

Determining If a Point Is a Solution
::确定一个点是否为解决办法

How can you determine whether the point (6, -2, 5) is a solution to the system below?
::您如何确定点( 6, 2, 5) 是否是以下系统的解决办法 ?

$\begin{aligned} x - y + z & = 13 \\ 2 x + 5 y - 3 z & = - 13 \\ 4 x - y - 6 z & = - 4 \end{aligned}$

::x- y+z=132x+5y- 3z- 134x- y-6z4

In order for the point to be a solution to the system, it must satisfy each of the three equations.
::要使这一点成为系统的解决办法,它必须满足三个方程式中的每一个方程式。

First equation: $\begin{aligned} (6) - (- 2) + (5) = 6 + 2 + 5 = 13 \end{aligned}$
::第一等式6)-(-2)+(5)=6+2+5=13

Second equation: $\begin{aligned} 2 (6) + 5 (- 2) - 3 (5) = 12 - 10 - 15 = - 13 \end{aligned}$
::第二个方程: 2(6)+5(-2)-3(5)=12-10-1513

Third equation: $\begin{aligned} 4 (6) - (- 2) - 6 (5) = 24 + 2 - 30 = - 4 \end{aligned}$
::第三等式:4(6)-(-2)-6(5)=24+2-304

The point, (6, -2, 5), satisfies all three equations. Therefore, it is a solution to the system.
::点(6,2,5)满足了所有三个方程式,因此,这是系统的解决办法。

Solving Systems
::解决系统

Solve the system using linear combinations:
::使用线性组合解决系统:

$\begin{aligned} 2 x + 4 y - 3 z & = - 7 \\ 3 x - y + z & = 20 \\ x + 2 y - z & = - 2 \end{aligned}$

::2x+4y-3z73x-y+z=20x+2y-z%2

We can start by taking two equations at a time and eliminating the same variable. We can use the first two equations to eliminate $\begin{aligned} z \end{aligned}$ . Then we can use the second and third equations to eliminate $\begin{aligned} z \end{aligned}$ .
::我们可以从一次两个方程式开始,然后消除同一个变量。我们可以用前两个方程式来消除z。然后我们可以用第二个和第三个方程式来消除z。

$\begin{aligned} 2 x + 4 y - 3 z = - 7 \Rightarrow 2 x + 4 y - 3 z = - 7 \\ 3 (3 x - y + z = 20) \underline{9 x - 3 y + 3 z = 60} \\ 11 x + y = 53 \end{aligned}$

::2x+4y-3z72x+4y-3z73(3x-y+z=20) 9x-3y+3z=60_11x+y=53

Result from equations 1 and 2: $\begin{aligned} 11 x + y = 53 \end{aligned}$
::方程1和2: 11x+y=53

$\begin{aligned} 3 x - y + z = 20 \\ \underline{x + 2 y - z = - 2} \\ 4 x + y = 18 \end{aligned}$

::3 - y+z=20x+2y - z2 - 4x+y=18 3 - y+z=20x+2y - z2 - 4x+y=18

Result from equations 2 and 3: $\begin{aligned} 4 x + y = 18 \end{aligned}$
::方程2和3:4x+y=18的结果

Now we have reduced our system to two equations in two variables. We can eliminate $\begin{aligned} y \end{aligned}$ most easily next, and solve for $\begin{aligned} x \end{aligned}$ .
::现在我们把我们的系统简化为两个变数中的两个方程式。我们可以最容易地删除下一个 y, 然后解决 x 。

$\begin{aligned} 11 x + y = 53 \Rightarrow 11 x + y = 53 \\ - 1 (4 x + y = 18) \underline{- 4 x - y = - 18} \\ 7 x = 35 \\ x = 5 \end{aligned}$

::11x+y=5311x+y=53-1(4x+y=18)-4x-y18_7x=35 x=5

Now use this value to find $\begin{aligned} y \end{aligned}$ :
::现在使用此值查找 y:

$\begin{aligned} 4 (5) + y & = 18 \\ 20 + y & = 18 \\ y & = - 2 \end{aligned}$

::4(5)+y=1820+y=18y @%2

Finally, we can go back to one of the original three equations and use our $\begin{aligned} x \end{aligned}$ and $\begin{aligned} y \end{aligned}$ values to find $\begin{aligned} z \end{aligned}$ .
::最后,我们可以回到原来的三个方程中的一个, 用我们的x值和y值来找到z。

$\begin{aligned} 2 (5) + 4 (- 2) - 3 z & = - 7 \\ 10 - 8 - 3 z & = - 7 \\ 2 - 3 z & = - 7 \\ - 3 z & = - 9 \\ z & = 3 \end{aligned}$

::2(5)+4(-2)-3z710-8-3z72-3z7-3z7-3z9z=3

Therefore, the solution is (5, -2, 3).
::因此,解决办法是(5,2,3)。

Don't forget to check your answer by substituting the point into each equation.
::别忘了检查你的答案将点换成每个方程

Equation 1: $\begin{aligned} 2 (5) + 4 (- 2) - 3 (3) = 10 - 8 - 9 = - 7 \end{aligned}$
::等式1: 2(5)+4(-2-2)-3(3)=10-8-97

Equation 2: $\begin{aligned} 3 (5) - (- 2) + (3) = 15 + 2 + 3 = 20 \end{aligned}$
::等式2: 3(5)-(-2)+(3)=15+2+3=20

Equation 3: $\begin{aligned} (5) + 2 (- 2) - (3) = 5 - 4 - 3 = - 2 \end{aligned}$
::等式35)+2(-2)-(3)=5-4-32

Solve this new system using linear combinations:
::使用线性组合解决这个新系统:

$\begin{aligned} x + y + z & = 5 \\ 5 x + 5 y + 5 z & = 20 \\ 2 x + 3 y - z & = 8 \end{aligned}$

::x+y+z=55x+5y+5z=202x+3y-z=8

We can start by combining equations 1 and 2 together by multiplying the first equation by -5.
::我们可以将方程1和2结合起来, 将第一个方程乘以 -5。

$\begin{aligned} - 5 (x + y + z = 5) \Rightarrow - 5 x - 5 y - 5 z = - 25 \\ 5 x + 5 y + 5 z = 20 \underline{5 x + 5 y + 5 z = 20} \\ 0 = - 5 \end{aligned}$

::5(x+y+z=5) 5(x+y+z=5) 5(5) 5(5) 5(5) 5(5) 5(5) 5(5) 5(5) 5(5) 5(5) 5(5) 5(5) 5(5) 5(5) 5(5) 5(5) 5(5) 5(5) 5(5) 5(5) 5(5) 5(5) 5(5) 5(5) 5(5) 5(5) 5(5) 20(0) 5(5)

Since the result is a false equation, there is no solution to the system. If you end up with 0 = 0, then there will be infinitely many solutions.
::由于结果是一个虚假的等式, 系统就没有解决方案。如果您以 0 = 0 结尾, 那么将会有很多解决方案。

Play, Learn, and Explore 3 Variable Systems : .
::播放、学习和探索 3 变量系统: 。

Examples
::实例

Example 1
::例1

In the Introduction, you were asked to find how much each fruit cost.
::在导言中,有人要求你找出每个水果的成本。

The system of linear equations represented by this situation is:
::以这种情况为代表的线性方程式系统是:

$\begin{aligned} 2 s + 5 g + m = 20 \\ 3 s + 2 g + 2 m = 21 \\ 4 s + 3 g + 3 m = 30 \end{aligned}$

::2s+5g+m=203s+2g+2m=214s+3g+3m=30

Solution:
::解决方案 :

Let's start by multiplying the first equation, $\begin{aligned} 2 s + 5 g + m = 20, \end{aligned}$ by 2. We obtain
::首先让我们把第一个方程乘以 2s+5g+m=20乘以2

$\begin{aligned} 4 s + 10 g + 2 m = 40. \end{aligned}$
::4s+10g+2m=40。

Now we can subtract the third equation from this equation :
::现在我们可以从这个方程中减去第三个方程:

$\begin{aligned} 4 s + 10 g + 2 m = 40 \\ \underline{4 s + 3 g + 3 m = 30} \\ 7 g - m = 10 \end{aligned}$

::4s+10g+2m=404s+3g+3m=30_7g-m=10

Now let's multiply the second equation by 4 and the third equation by 3. We obtain:
::现在让我们把第二个方程乘以4 第三个方程乘以3 我们获得:

$\begin{aligned} 12 s + 8 g + 8 m = 84 \\ 12 s + 9 g + 9 m = 90 \end{aligned}$

::12s+8g+8m=8412s+9g+9m=90

Now we can subtract the new third equation from the new second equation:
::现在,我们可以从新的第二个方程中减去新的第三个方程:

$\begin{aligned} 12 s + 8 g + 8 m = 84 \\ \underline{12 s + 9 g + 9 m = 90} \\ - g - m = - 6 \end{aligned}$

::12s+8g+8m=8412s+9g+9m=90_-g-m6

If we multiply this result by 7 and add it to the result we obtain above , we obtain:
::如果我们将这一结果乘以7, 并将其加到上述结果中, 我们就会得到:

$\begin{aligned} 7 g - m = 10 \\ \underline{- 7 g - 7 m = - 42} \\ - 8 m = - 32 \end{aligned}$

::7-m=10-7-7g-7m_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

This implies $\begin{aligned} m = 4 \end{aligned}$ . We can substitute this value of m into the previous equation to obtain the value of g :
::这意味着 m=4。我们可以将 m 值替换为前一个方程, 以获得 g 值 :

$\begin{aligned} 7 g - (4) = 10 \\ 7 g = 14 \\ g = 2 \end{aligned}$

::7g-(4)=107g=14g=2

Finally, we substitute these values for m and g into one of our original equations to determine the value of s :
::最后,我们将这些 m 和 g 的值替换成我们原先的方程之一,以确定 s 的值:

$\begin{aligned} 2 s + 5 (2) + (4) = 20 \\ 2 s + 14 = 20 \\ 2 s = 6 \\ s = 3 \end{aligned}$

::2s+5(2)+(4)=202s+14=202s=6s=3

Therefore, squash cost $3 per pound, green beans cost $2 per pound, and melon costs $4 per pound.
::因此,南瓜每磅3美元,绿豆每磅2美元,瓜每磅4美元。

Example 2
::例2

Is the point (-3, 2, 1) a solution to the system below?
::这一点(-3,2,1)是否是以下系统的解决办法?

$\begin{aligned} x + y + z & = 0 \\ 4 x + 5 y + z & = - 1 \\ 3 x + 2 y - 4 z & = - 8 \end{aligned}$

::x+y+z=04x+5y+z13x+2y_4z_8

Solution:
::解决方案 :

Check to see if the point satisfies all three equations.
::检查点是否满足所有三个方程式。

Equation 1: $\begin{aligned} (- 3) + (2) + (1) = - 3 + 2 + 1 = 0 \end{aligned}$
::等式 1: (-3) +(2) +(1) + 3+2+1=0

Equation 2: $\begin{aligned} 4 (- 3) + 5 (2) + (1) = - 12 + 10 + 1 = - 1 \end{aligned}$
::等式 2: 4(-3)+5(2)+(1)12+10+1+1

Equation 3: $\begin{aligned} 3 (- 3) + 2 (2) - 4 (1) = - 9 + 4 - 4 = - 9 \neq - 8 \end{aligned}$
::等量 33-3)、+2(2)-4(1)、9+4-4-4(9)8

Since the third equation is not satisfied by the point, the point is not a solution to the system.
::由于第三种方程式不能满足这一点,因此问题不是系统的解决办法。

Example 3
::例3

Solve the following system using linear combinations:
::使用线性组合解决以下系统:

$\begin{aligned} 5 x - 3 y + z & = - 1 \\ x + 6 y - 4 z & = - 17 \\ 8 x - y + 5 z & = 12 \end{aligned}$

::5-3y+z1x+6y-4z178x-y+5z=12

Solution:
::解决方案 :

Combine the first and second equations to eliminate $\begin{aligned} z \end{aligned}$ . Then combine the first and third equations to eliminate $\begin{aligned} z \end{aligned}$ .
::合并第一和第二方程式来消除z。然后合并第一和第二方程式来消除z。然后合并第一和第二方程式来消除z。

$\begin{aligned} 4 (5 x - 3 y + z = - 1) \Rightarrow 20 x - 12 y + 4 z = - 4 \\ x + 6 y - 4 z = - 17 \underline{x + 6 y - 4 z = - 17} \\ 21 x - 6 y = - 21 \end{aligned}$

::4( 5x-3y+z1) 20x- 12y+4z4x+6y- 4z17 x+6y- 4z17_ 21x-6y21

Result from equations 1 and 2: $\begin{aligned} 21 x - 6 y = - 21 \end{aligned}$
::方程1和2产生结果:21x-6y21

$\begin{aligned} - 5 (5 x - 3 y + z = - 1) \Rightarrow - 25 x + 15 y - 5 z = 5 \\ 8 x - y + 5 z = 12 \underline{8 x - y + 5 z = 12} \\ - 17 x + 14 y = 17 \end{aligned}$

::-5(5x-3y+z1)-25x+15y=5z=58x-y+5z=12 8x-y+5z=12x-y+5z=12+17x+14y=17

Result from equations 1 and 3: $\begin{aligned} - 17 x + 14 y = 17 \end{aligned}$
::方程1和3的结果: - 17x+14y=17

Now we have reduced our system to two equations in two variables. We can eliminate $\begin{aligned} y \end{aligned}$ most easily next, and solve for $\begin{aligned} x \end{aligned}$ .
::现在我们把我们的系统简化为两个变数中的两个方程式。我们可以最容易地删除下一个 y, 然后解决 x 。

$\begin{aligned} 7 (21 x - 6 y = - 21) \Rightarrow 147 x - 42 y = - 147 \\ 3 (- 17 x + 14 y = 17) \underline{- 51 x + 42 y = 51} \\ 96 x = - 96 \\ x = - 1 \end{aligned}$

::7(21x-6y 21) 147x-42y 14773(- 17x+14y=17) − 51x+42y=51_ 96x_ 96x_ 96x_ 1)

Now find $\begin{aligned} y \end{aligned}$ :
::现在找到 y :

$\begin{aligned} 21 (- 1) - 6 y & = - 21 \\ - 21 - 6 y & = - 21 \\ - 6 y & = 0 \\ y & = 0 \end{aligned}$

::21 - 6y=0y=0 21 - 21 - 21 - 6y _ 21 - 6y=0

Finally, we can go back to one of the original three equations and use our $\begin{aligned} y \end{aligned}$ and $\begin{aligned} z \end{aligned}$ values to find $\begin{aligned} x \end{aligned}$ .
::最后,我们可以回到原来的三个方程中的一个, 用我们的y和z值来找到x。

$\begin{aligned} 5 (- 1) - 3 (0) + z & = - 1 \\ - 5 + z & = - 1 \\ z & = 4 \end{aligned}$

::5(-1)-3(0)+z1-5+z1z=4

Therefore, the solution is (-1, 0, 4).
::因此,解决办法是(1,0,4)。

Don't forget to check your answer by substituting the point into each equation.
::别忘了检查你的答案将点换成每个方程

Equation 1: $\begin{aligned} 5 (- 1) - 3 (0) + (4) = - 5 + 4 = - 1 \end{aligned}$
::等式 1 : 5(-1)- 3(0)+(4) 5+41

Equation 2: $\begin{aligned} (- 1) + 6 (0) - 4 (4) = - 1 - 16 = - 17 \end{aligned}$
::等式 2: (-1) +6(0)-4(4) 1-16 17

Equation 3: $\begin{aligned} 8 (- 1) - (0) + 5 (4) = - 8 + 20 = 12 \end{aligned}$
::等式 3: 8(-1)-(0)+5(4) 8+20=12

Example 4
::例4

Solve the following system using elimination :
::使用消除方法解决以下系统:

$\begin{aligned} 2 x + y - z & = 3 \\ x - 2 y + z & = 5 \\ 6 x + 3 y - 3 z & = 6 \end{aligned}$

::2x+y-z=3x-2y+z=56x+3y-3z=6

Solution :
::解决方案 :

Combine equations 1 and 2 to eliminate $\begin{aligned} z \end{aligned}$ . Then combine equations 2 and 3 to eliminate $\begin{aligned} z \end{aligned}$ .
::组合方程式1和2来消除z。然后合并方程式2和3来消除z。

$\begin{aligned} 2 x + y - z = 3 \\ \underline{x - 2 y + z = 5} \\ 3 x - y = 8 \end{aligned}$

::2x+y-z=3x-2y+z=5_3x-y=8

Result from equations 1 and 2: $\begin{aligned} 3 x - y = 8 \end{aligned}$
::公式1和公式2的结果:3x-y=8

$\begin{aligned} 3 (x - 2 y + z = 5) \Rightarrow 3 x - 6 y + 3 z = 15 \\ 6 x + 3 y - 3 z = 6 \underline{6 x + 3 y - 3 z = 6} \\ 9 x - 3 y = 21 \end{aligned}$

::3(x-2y+z=5)3x-6y+3z=156x+3y-3z=66x+3y-3z=6_9x-3y=21)

Result from equations 2 and 3: $\begin{aligned} 9 x - 3 y = 21 \end{aligned}$
::等方2和3: 9x-3y=21

Now we have reduced our system to two equations in two variables. Now we can combine these two equations and attempt to eliminate another variable.
::现在我们把我们的系统简化为两个变量中的两个方程式。现在我们可以把这两个方程式结合起来, 并尝试去掉另一个变量。

$\begin{aligned} - 3 (3 x - y = 8) \Rightarrow - 9 x + 3 y = - 24 \\ 9 x - 3 y = 21 \underline{9 x - 3 y = 21} \\ 0 = - 3 \end{aligned}$

::- 3(3x-y=8)-9x+3y24 9x-3y=219x-3y=21_03

Since the result is a false equation, there is no solution to the system.
::由于结果是虚假的等式,对该系统没有解决办法。

Summary
::摘要

A minimum of three equations is necessary to solve a system with three variables .
::至少需要三个方程式才能解决一个有三个变量的系统。

The elimination method can be used t o solve a system of three variables in three equations.
::消除方法可用于在三个方程式中解决三个变量的系统。

There can be three possible results when solving systems of three linear equations: one solution, infinitely many solutions, and no solution.
::在解决三个线性方程式的系统时,可以有三种可能的结果:一种解决办法,无限多的解决办法,而没有解决办法。

Review
::回顾

Is the point (2, -3, 5) the solution to the system below?
::问题(2,3,5)是解决以下系统的办法吗?

$\begin{aligned} 2 x + 5 y - z & = - 16 \\ 5 x - y - 3 z & = - 2 \\ 3 x + 2 y + 4 z & = 20 \end{aligned}$

::2x+5y-z=-165x-y-3z=-23x+2y+4z=20

Is the point (-1, 3, 8) the solution to the system below?
::点(-1, 3, 8)是以下系统的解决办法吗?

$\begin{aligned} 8 x + 10 y - z & = 14 \\ 11 x + 4 y - 3 z & = - 23 \\ 2 x + 3 y + z & = 10 \end{aligned}$

::8x+10y-z=1411x+4y-3z=232x+3y+z=10

Is the point (0, 3, 5) the solution to the system below?
::点(0, 3, 5)是以下系统的解决办法吗?

$\begin{aligned} 5 x - 3 y + 2 z & = 1 \\ 7 x + 2 y - z & = 1 \\ x + 4 y - 3 z & = - 3 \end{aligned}$

::5x-3y+2z=17x+2y-z=1x+4y-3z=3

Is the point (1, -1, 1) the solution to the system below?
::点(1,-1,1)是以下系统的解决办法吗?

$\begin{aligned} x - 2 y + 2 z & = 5 \\ 6 x + y - 4 z & = 1 \\ 4 x - 3 y + z & = 8 \end{aligned}$

::x-2y+2z=56x+y-4z=14x-3y+z=8

Solve the systems below in three variables using linear combinations.
::使用线性组合,用三个变量解决以下系统。

.

$\begin{aligned} 3 x - 2 y + z & = 0 \\ 4 x + y - 3 z & = - 9 \\ 9 x - 2 y + 2 z & = 20 \end{aligned}$

.

$\begin{aligned} 11 x + 15 y + 5 z & = 1 \\ 3 x + 4 y + z & = - 2 \\ 7 x + 13 y + 3 z & = 3 \end{aligned}$

.

$\begin{aligned} 2 x + y + 7 z & = 5 \\ 3 x - 2 y - z & = - 1 \\ 4 x - y + 3 z & = 5 \end{aligned}$

.

$\begin{aligned} x + 3 y - 4 z & = - 3 \\ 2 x + 5 y - 3 z & = 3 \\ - x - 3 y + z & = - 3 \end{aligned}$

.

$\begin{aligned} 3 x - 2 y - 5 z & = - 8 \\ 3 x + 2 y + 5 z & = - 8 \\ 6 x + 4 y - 10 z & = - 16 \end{aligned}$

.

$\begin{aligned} x + 2 y - z & = - 1 \\ 2 x + 4 y + z & = 10 \\ 3 x - y + 8 z & = 6 \end{aligned}$

.

$\begin{aligned} x + y - z & = - 3 \\ 2 x - y - z & = 6 \\ 4 x + y + z & = 0 \end{aligned}$

.

$\begin{aligned} 4 x + y + 3 z & = 8 \\ 8 x + 2 y + 6 z & = 15 \\ 3 x - 3 y - z & = 5 \end{aligned}$

.

$\begin{aligned} 2 x + 3 y - z & = - 1 \\ x + 2 y + 3 z & = - 4 \\ - x + y - 2 z & = 3 \end{aligned}$

.

$\begin{aligned} x - 3 y + 4 z & = 14 \\ - x + 2 y - 5 z & = - 13 \\ 2 x + 5 y - 3 z & = - 5 \end{aligned}$

.

$\begin{aligned} x + y + z & = 3 \\ x + y - z & = 3 \\ 2 x + 2 y + z & = 6 \end{aligned}$

16. When Kaitlyn went to the store with $10, she had some choices about what to buy. She could get one apple, one onion, and one basket of blueberries for $9. She could get two apples and two onions for $10. She could also get two onions and one basket of blueberries for $10. Write and solve a system of linear equations.

::16. Kaitlyn带着10美元去商店时,她对买什么有一些选择,她可以买一个苹果、一个洋葱和一篮蓝莓9美元,她可以买两个苹果和两个洋葱10美元,她也可以买两个洋葱和一篮蓝莓10美元,写和解决线性方程系统。

17. The sum of the digits of a three-digit number is 15. The tens digits is four less than the hundreds digit, and the units digit is five less than the sum of the other two digits. What is the number?
::17. 三位数数字的数字总和是15。十位数比百位数少四位数,单位数比其他两位数的数字总和少五位数。数字是多少?

18. John has $42,000 to invest. He invests a portion of this money into a savings account paying 5% interest, a time deposit paying 7%, and a bond paying 9%. He earned $2,600 in annual interest from these three investments. If the earned interest from the savings account was $200 less than the sum of earned interest from the other two investments, how much did John invest in each type of investment?
::18. 约翰有42 000美元的投资,他将这笔钱的一部分投资于一个支付5%利息的储蓄账户,7%的定期存款,9%的债券,他从这三项投资中赚取年利息2 600美元,如果储蓄账户所得利息比另外两项投资所得利息少200美元,约翰对每种投资的投资额是多少?

19. A cashier has 25 coins consisting of nickels, dimes, and quarters with a value of $3.95. If the number of quarters is two less than twice the number of nickels, how many of each type of coin does the cashier have?

::19. 出纳员有25个硬币,由镍、硬币和硬币组成,价值3.95美元,如果季度数目比镍少两倍,出纳员每种硬币有多少?

20. A theater sells tickets at $6 for adults, $4 for students, and $3 for children under 12 years old. A total of 260 tickets were sold for one showing, with a total revenue of $1,200. If the number of adult tickets sold was three times the number of student tickets sold, how many of each type of ticket were sold for the showing?
::20. 一家剧院售票为成人6美元,学生4美元,12岁以下儿童3美元,共售票260张,一个演出的总收入为1 200美元,如果售出的成人票数是售出学生票数的三倍,每张票中售出多少张?

Review ( Answers)
::回顾(答复)

Please see the Appendix.
::请参看附录。

Section outline

Introduction ::导言

Linear Systems in Three Variables ::三个变量中的线性系统

Determining If a Point Is a Solution ::确定一个点是否为解决办法

Solving Systems ::解决系统

Examples ::实例

Summary ::摘要

Review ::回顾

Review ( Answers) ::回顾(答复)

Introduction
::导言

Linear Systems in Three Variables
::三个变量中的线性系统

Determining If a Point Is a Solution
::确定一个点是否为解决办法

Solving Systems
::解决系统

Examples
::实例

Summary
::摘要

Review
::回顾

Review ( Answers)
::回顾(答复)