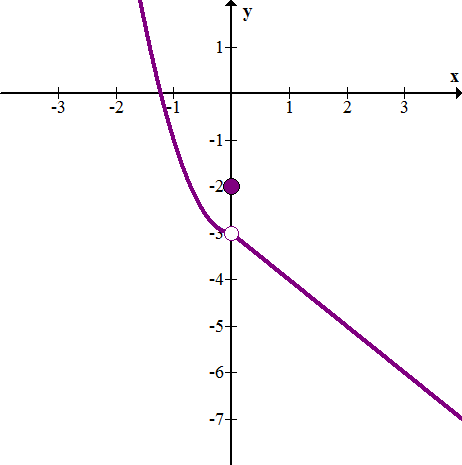Section: 连续连续性 | 15.7 连续性

Section outline

Introduction
::导言

Suppose Jack is traveling around his neighborhood. First he is walking, but then switches to riding his bike. His velocity is modeled by the piecewise function below. Is the piecewise function continuous on the interval $\begin{aligned} x > 0 \end{aligned}$ ?
::假设杰克在附近旅行。首先他走路, 然后开关骑自行车。他的速度以下面的片段函数为模型。片段函数是否在间距 x>0 上连续进行 ?

$\begin{aligned} f (x) = {\begin{cases} - x - 2 0 < x < 1 \\ - 3 x = 1 \\ x^{2} - 4 1 < x \end{cases} \end{aligned}$

:xx) x- 20 <x < 1 - 3 x=1x2 - 4 - 1 <x

Continuity
::连续连续性

In the past, you may have defined continuity as the ability to draw a function completely without lifting your pencil off the paper. If a function could be drawn without lifting your pencil, then it was continuous. If a function could not be drawn without lifting your pencil, then it had some sort of discontinuity and was not a continuous function. You can now define continuity with a more rigorous definition using limits.
::过去,您可能将连续性定义为在不从纸上举起铅笔的情况下完全绘制一个函数的能力。如果可以不举起铅笔而绘制一个函数,那么它就是连续的。如果不能在不举起铅笔的情况下绘制一个函数,那么它就具有某种不连续性,而不是连续的功能。现在,您可以用一个更严格的限制定义来定义连续性。

Continuity
::连续连续性

A function $\begin{aligned} f (x) \end{aligned}$ is continuous at $\begin{aligned} x = a \end{aligned}$ if:
::函数 f( x) 在 x=a 时是连续的, 如果 :

$\begin{aligned} f (a) \end{aligned}$ exists
:f(a) 存在

$\begin{aligned} lim_{x \to a} f (x) \end{aligned}$ exists
::limxaf( x) 存在

The limit of the function is equal to the function value at $\begin{aligned} x = a \end{aligned}$ .
$\begin{aligned} lim_{x \to a} f (x) = f (a) \end{aligned}$

::函数的极限等于 x=a.limxaf(x) =f(a) 的函数值

A function is continuous over an interval if it is continuous at each point in that interval.
::一个函数如果在该间隔的每个点是连续的,则该函数是一个间隔的连续。

The following video further discusses continuity with limits:
::以下影片进一步讨论有限度的连续性:



Play, Learn, and Explore Continuity:
::游戏、学习和探索连续性:

Examples
::实例

Example 1
::例1

Where is the function graphed below discontinuous?
::在不连续状态下绘制的函数图在哪里 ?

Solution:
::解决方案 :

The function is discontinuous at $\begin{aligned} x = - 5, - 1, 3, and 5 \end{aligned}$ because the limit does not exist at each of these points.
::3⁄4 ̄ ̧漯B

Example 2
::例2

Is the following function continuous?
::下列功能是否连续?

$\begin{aligned} f (x) = {\begin{cases} x^{2} - 1 x < - 1 \\ 3 x = - 1 \\ - x + 3 - 1 < x \end{cases} \end{aligned}$

::f( x) x2 - 1 x13 x1 - x+3 - 1 < x

Solution :
::解决方案 :

The piecewise function is continuous if every point of the function is continuous. All $\begin{aligned} x \end{aligned}$ -values must then be checked where the piecewise function changes from one piece to another. For the given function, the $\begin{aligned} x \end{aligned}$ -value where the piecewise function changes from one piece to another is $\begin{aligned} x = - 1 \end{aligned}$ .
::如果函数的每个点都是连续的, 片段函数是连续的。然后必须检查所有 x 值, 当片段函数从一个部分向另一个部分变化。对于给定的函数, 片段函数从一个部分向另一个部分变化的 x 值是 x\\\ 1 。

Using the definition of continuity:
::使用连续性的定义:

$\begin{aligned} f (- 1) = 3 \end{aligned}$

::f(-1)=3

$\begin{aligned} lim_{x \to 1^{-}} f (x) = (- 1)^{2} - 1 = 1 - 1 = 0 \end{aligned}$

::立方公尺x_1- f(x) = (- 1) 2 - 1= 1 - 1= 1=0

$\begin{aligned} lim_{x \to - 1^{+}} f (x) = - 1 + 3 = 2. \end{aligned}$

::limx1+f(x) 1+3=2。

Since the two are not equal, the limit of the function does not exist.
$\begin{aligned} lim_{x \to a^{-}} f (x) \neq lim_{x \to a^{+}} f (x) \end{aligned}$

::由于两者不相等,函数的极限不存在。 limxa- f( x) limxa+f( x)

Thus, this function is discontinuous at $\begin{aligned} x = - 1 \end{aligned}$ .
::因此,此函数在 x% 1 时不连续。

Example 3
::例3

On what intervals is the function in Example 2 continuous?
::例2中函数的间隔是连续的?

Solution:
::解决方案 :

The function is continuous on the intervals $\begin{aligned} x < - 1 and x > - 1 \end{aligned}$ .
::此函数在间隔 x1 和 x1 上是连续的。

Example 4
::例4

Recall the problem from the Introduction: Jack is first walking around his neighborhood, and then switches to riding his bike. Is the piecewise function continuous on the interval $\begin{aligned} x > 0 \end{aligned}$ ?
::回顾引言中的问题:杰克首先在附近走动,然后开动开关,骑自行车。片段函数是否在间距 x>0 上持续?

$\begin{aligned} f (x) = {\begin{cases} - x - 2 0 < x < 1 \\ - 3 x = 1 \\ x^{2} - 4 1 < x \end{cases} \end{aligned}$

:xx) x- 20 <x < 1 - 3 x=1x2 - 4 - 1 <x

Solution:
::解决方案 :

The piecewise function is continuous on the interval if every point of the function on the interval is continuous. All $\begin{aligned} x \end{aligned}$ -values must then be checked where the piecewise function changes from one piece to another. For the given function, the $\begin{aligned} x \end{aligned}$ -value where the piecewise function changes from one piece to another is $\begin{aligned} x = 1 \end{aligned}$ .
::如果间隔中函数的每个点都是连续的, 则字符串函数在间隔中是连续的。然后必须检查所有 x 值, 以哪个字符顺序函数从一个字符转换到另一个。对于给定的函数, 字符串函数从一个字符转换到另一个函数的 x 值是 x=1 。

Using the definition of continuity:
::使用连续性的定义:

$\begin{aligned} f (1) = - 3 \end{aligned}$

::f(1) 3

$\begin{aligned} lim_{x \to 1^{-}} f (x) = - 1 - 2 = - 3 \end{aligned}$

::立方公尺

$\begin{aligned} lim_{x \to 1^{+}} f (x) = 1^{2} - 4 = - 3. \end{aligned}$

::立方公尺x1+f(x)=12-43。

Since the two one-sided limits are equal, the limit of the function at $\begin{aligned} x = 1 \end{aligned}$ exists.
::由于两个单向限制是相等的, x=1 的函数限制是存在的。

$\begin{aligned} lim_{x \to 1} f (x) = - 3 \end{aligned}$

::立方公尺

Since the limit value and the function value at $\begin{aligned} x = 1 \end{aligned}$ are equal, both are equal to -3, the function is continuous at $\begin{aligned} x = 1 \end{aligned}$ . Also, the function is continuous to the left and right of $\begin{aligned} x = 1 \end{aligned}$ , so the piecewise function is continuous on the interval.
::由于限制值和 x=1 的函数值相等, 两者均等于 - 3, 函数在 x=1 时是连续的。另外, 函数在 x=1 的左侧和右侧是连续的, 因此, 片段函数在间隔内是连续的。

Example 5
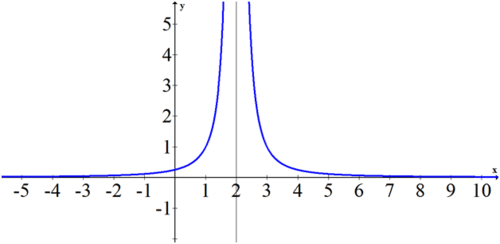
::例5

Megan argues that according to the definition of continuity, the function below is continuous. She says
::Megan认为,根据连续性的定义,以下职能是连续性的。

$\begin{aligned} lim_{x \to 2^{-}} f (x) = \infty \end{aligned}$

::立方公尺x%2-f(x) ___________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

$\begin{aligned} lim_{x \to 2^{+}} f (x) = \infty \end{aligned}$

::立方公尺x%2+f(x){______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

$\begin{aligned} f (2) = \infty . \end{aligned}$

::f (2) 。

Since $\begin{aligned} lim_{x \to 2^{-}} f (x) = f (2) = lim_{x \to 2^{+}} f (x) \end{aligned}$ , it meets the definition of continuous.
::由于limx%2-f(x)=f(2)=limx%2+f(x),它符合连续的定义。

How could you use the graph below to clarify Megan's reasoning?
::你怎么能用下面的图表来澄清梅根的推理呢?

Solution:
::解决方案 :

Megan is being extremely liberal with the idea of $\begin{aligned} = \infty \end{aligned}$ . Remember that when a limit approaches infinity, the limit does not exist. Two limits that do not exist cannot be equal to one another. Also, the function is undefined at $\begin{aligned} x = 2 \end{aligned}$ .
::Megan对 {{{{{{{}}} 的概念非常自由。记住当限制方法无限时, 限制并不存在。两个不存在的限制不能相互等同。另外, 函数在 x=2 时未定义。

Example 6
::例6

The function $\begin{aligned} f (x) = \tan x \end{aligned}$ is not continuous. However, determine an interval in which $\begin{aligned} f (x) \end{aligned}$ is continuous.
::函数 f( x) =tanx 不是连续的。但是, 确定 f( x) 是连续的间隔。

Solution:
::解决方案 :

While $\begin{aligned} \tan x \end{aligned}$ is not continuous everywhere, it is continuous over certain intervals. One such interval is $\begin{aligned} - \frac{π}{2} < x < \frac{π}{2} \end{aligned}$ . Another possible interval is $\begin{aligned} \frac{π}{2} < x < \frac{3 π}{2} \end{aligned}$ .
::虽然 tanx 不是随处可见的连续, 但它在一定的间隔内是连续的。其中一种间隔是 2 < x2 。另一种可能的间隔是 2 < x < 32 。

Example 7
::例7

What must $\begin{aligned} k \end{aligned}$ be equal to in order for the following piecewise function to be continuous?
::要连续进行以下的片段函数,K必须等于什么?

$\begin{aligned} f (x) = {\begin{cases} 4 x - 5 x < 2 \\ k x = 2 \\ - 2 x + 7 x > 2 \end{cases} \end{aligned}$

:x) f=4x-5x <2kx=2-2x+7x>2

Solution :
::解决方案 :

Using the definition of continuity:
::使用连续性的定义:

$\begin{aligned} f (2) = k \end{aligned}$

::f(2)=k

$\begin{aligned} lim_{x \to 2^{-}} f (x) = 4 (2) - 5 = 3 \end{aligned}$

::立方公尺x%2- f(x)=4(2)-5=3

$\begin{aligned} lim_{x \to 2^{+}} f (x) = - 2 (2) + 7 = 3 \end{aligned}$

::limx%2+f(x) @%2(2)+7=3

Since the two one-sided limits equal, the limit of the function at $\begin{aligned} x = 2 \end{aligned}$ exists.
::由于两个单向限制相等, x=2 函数的极限存在。

$\begin{aligned} lim_{x \to 2} f (x) = 3 \end{aligned}$

::limx%2f(x)=3

In order for the piecewise function to be continuous, it must be continuous at every point, including $\begin{aligned} x = 2 \end{aligned}$ . Thus, the limit value and the function value at $\begin{aligned} x = 2 \end{aligned}$ must be equal.
::要使片段函数连续,它必须在每一点连续,包括 x=2。因此, x=2 的限值和函数值必须是相等的。

$\begin{aligned} lim_{x \to 2} f (x) = f (2) \end{aligned}$
So, $\begin{aligned} k = 3 \end{aligned}$ .
::立方公尺x%2f(x)=f(2) So, k=3。

Summary
::摘要

A function $\begin{aligned} f (x) \end{aligned}$ is continuous at $\begin{aligned} x = a \end{aligned}$ if $\begin{aligned} lim_{x \to a} f (x) = f (a), \end{aligned}$ where both $\begin{aligned} f (a) \end{aligned}$ and $\begin{aligned} lim_{x \to a} f (x) \end{aligned}$ exist.
::函数 f( x) 在 x=a 存在 f( a) 和 limx- af( x) 的 x 和 limx- af( x) 的 x 上是连续的。

::函数 f( x) 在 x=a 存在 f( a) 和 limx- af( x) 的 x 和 limx- af( x) 的 x 上是连续的。

A function is continuous over an interval if it is continuous at each point in that interval.

::一个函数如果在该间隔的每个点是连续的,则该函数是一个间隔的连续。

Review
::回顾

Consider
$\begin{aligned} f (x) = {\begin{cases} 2 x^{2} - 1 & x < 1 \\ 1 & x = 1 \\ - x + 2 & 1 < x \end{cases} \end{aligned}$

::考虑 f( x)\%% 2x2 - 1x < 1x 1x=1- x+21 < x

1. What is $\begin{aligned} lim_{x \to 1^{-}} f (x) \end{aligned}$ ?
::1. 什么是立方公尺1-f(x)?

2. What is $\begin{aligned} lim_{x \to 1^{+}} f (x) \end{aligned}$ ?
::2. 什么是limx1+f(x)?

3. Is $\begin{aligned} f (x) \end{aligned}$ continuous at $\begin{aligned} x = 1 \end{aligned}$ ?
::3. f(x) 在x=1时连续持续吗?

Consider
$\begin{aligned} g (x) = {\begin{cases} 4 x^{2} + 2 x - 1 & x < - 2 \\ 8 & x = - 2 \\ - 3 x + 5 & - 2 < x \end{cases} \end{aligned}$

::考虑 g( x)\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\

4. What is $\begin{aligned} lim_{x \to - 2^{-}} g (x) \end{aligned}$ ?
::4. 什么是limx2-g(x)?

5. What is $\begin{aligned} lim_{x \to - 2^{+}} g (x) \end{aligned}$ ?
::5. 什么是limx2+g(x)?

6. Is $\begin{aligned} g (x) \end{aligned}$ continuous at $\begin{aligned} x = - 2 \end{aligned}$ ?
::6. g(x) 在 x @ @% 2 时连续吗?

Consider $\begin{aligned} h (x) \end{aligned}$ shown in the graph below.
::考虑下图中显示的h(x) 。

7. What is $\begin{aligned} lim_{x \to 0^{-}} h (x) \end{aligned}$ ?
::7. 什么是limx0-h(x)?

8. What is $\begin{aligned} lim_{x \to 0^{+}} h (x) \end{aligned}$ ?
::8. 什么是limx=0+h(x)?

9. What is $\begin{aligned} h (0) \end{aligned}$ ?
::9. 什么是H(0)?

10. Is $\begin{aligned} h (x) \end{aligned}$ continuous at $\begin{aligned} x = 0 \end{aligned}$ ?
::10. h(x) 在x=0时连续持续吗?

11. The function $\begin{aligned} f (x) = \frac{1}{x} \end{aligned}$ is not continuous. However, determine an interval in which $\begin{aligned} f (x) \end{aligned}$ is continuous.
::11. F( x) =1x 函数不是连续的。但是, 确定 f( x) 是连续的间隔。

12. The function $\begin{aligned} g (x) = \sec x \end{aligned}$ is not continuous. However, determine an interval in which $\begin{aligned} g (x) \end{aligned}$ is continuous.
::12. 函数 g( x) =secx 不是连续的。但是, 确定 g( x) 是连续的间隔。

What must $\begin{aligned} k \end{aligned}$ be equal to in order for the following piecewise function to be continuous?
::要连续进行以下的片段函数,K必须等于什么?

13. $\begin{aligned} f (x) = {\begin{cases} 3 x + 1 x < - 2 \\ k x = - 2 \\ - 2 x - 1 x > - 2 \end{cases} \end{aligned}$
::13. f(x) 3x1x2x2x2x2x1x1x2

14. $\begin{aligned} g (x) = {\begin{cases} x^{2} - 3 x < 2 \\ k x = 2 \\ - 2 x + 5 x > 2 \end{cases} \end{aligned}$
::14. g(x) x2 - 3x < 2kx=2 - 2x+5x>2

15. $\begin{aligned} k (x) = {\begin{cases} 3 x - 6 x < 1 \\ k x = 1 \\ x^{3} - 4 x > 1 \end{cases} \end{aligned}$
::15. kk( x) 3x- 6x < 1kx= 1x3- 4x > 1

Review (Answers)
::回顾(答复)

Please see the Appendix.
::请参看附录。

Section outline

Introduction ::导言

Continuity ::连续连续性

Continuity ::连续连续性

Examples ::实例

Summary ::摘要

Review ::回顾

Review (Answers) ::回顾(答复)

Introduction
::导言

Continuity
::连续连续性

Continuity
::连续连续性

Examples
::实例

Summary
::摘要

Review
::回顾

Review (Answers)
::回顾(答复)