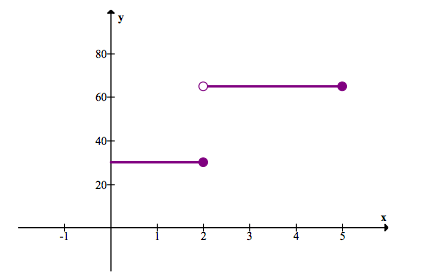节: 答案 - Ch 15: 微积分预览 | 16.15 答复----Ch 15:微积分预览

章节大纲

Section 15.2: Limit Notation
::第15.2节:限制说明

$\begin{align*}\lim\limits_{x\to\infty}{\tfrac{2x^4+4x^2-1}{5x^4+3x+9}=\lim\limits_{x\to\text{-}\infty}{\tfrac{2x^4+4x^2-1}{5x^4+3x+9}}}=\tfrac{2}{5}\end{align*}$
::立方公尺xx2x4+4x2-15x4+3x3x+9=limx%-2x4+4x2-15x4+3x9=25

$\begin{align*}\lim\limits_{x\to\infty}{\tfrac{8x^3+4x^2-1}{2x^3+4x+7}=\lim\limits_{x\to\text{-}\infty}{\tfrac{8x^3+4x^2-1}{2x^3+4x+7}}}=4\end{align*}$
::8x3+4x2 - 12x3+4x+7=limx}=========================================================================================================================================================================================================================================================================================================================================================================================================================================== = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =

$\begin{align*}\lim\limits_{x\to\infty}{\tfrac{x^2+2x^3-3}{5x^3+x+4}=\lim\limits_{x\to\text{-}\infty}{\tfrac{x^2+2x^3-3}{5x^3+x+4}}}=\tfrac{2}{5}\end{align*}$
::limxxx2+2x3 - 35x3+4=limx}==25=limx}=x2+2x3+353+x4=25

$\begin{align*}\lim\limits_{x\to\infty}{\tfrac{4x+4x^2-5}{2x^2+3x+3}=\lim\limits_{x\to\text{-}\infty}{\tfrac{4x+4x^2-5}{2x^2+3x+3}}}=2\end{align*}$
::立方公尺=2

$\begin{align*}\lim\limits_{x\to\infty}{\tfrac{3x^2+4x^3+4}{6x^3+3x^2+6}=\lim\limits_{x\to\text{-}\infty}{\tfrac{3x^2+4x^3+4}{6x^3+3x^2+6}}}=\tfrac{2}{3}\end{align*}$
::立方英寸3x2+4x3+46x3+3x2+6=limx}==============================================================================================================================================================================================================================

$\begin{align*}\lim\limits_{x\to{3}}{2x^2+1}=19\end{align*}$
::limx% 32x2+1=19

$\begin{align*}\lim\limits_{x\to\text{-}\infty}{e^x}=0\end{align*}$
::立方公尺=0

$\begin{align*}\lim\limits_{x\to\infty}{\frac{1}{x}=0}\end{align*}$
::limx1x=0

$\begin{align*}\lim\limits_{n\to\infty}{\sum_{i=1}^{n}{\left(\tfrac{1}{4}\right)^i}}=\tfrac{1}{3}\end{align*}$
::立方厘米=1( 14) 立方公尺=13

$\begin{align*}\lim\limits_{n\to\infty}{\sum_{i=1}^{n}{\frac{1}{i}}}\end{align*}$ does not exist
::limnni=11i 不存在

$\begin{align*}\lim\limits_{n\to\infty}{\sum_{i=0}^{n}{\left(\frac{1}{2}\right)^i}}=2\end{align*}$
::立方公尺=0( 12) i=2

$\begin{align*}\lim\limits_{n\to\infty}{\sum_{i=1}^{n}{\frac{9}{10^i}}}=1\end{align*}$
::立方公尺=1910i=1

The limit of $\begin{align*}f(x) = \frac{5x^2-4}{x+1}\end{align*}$ as $\begin{align*}x\end{align*}$ approaches 0 is -4.
::f(x) = 5x2-4x+1 的限值,作为 x local 0 是 - 4 。

The limit of $\begin{align*}y = \frac{x^3-1}{x-1}\end{align*}$ as $\begin{align*}x\end{align*}$ approaches 1 is 3.
::y=x3 - 1x-1 的极限值为 x 方法1 x 的极限值为 3 。

Yes, it's possible as long as $\begin{align*}a\end{align*}$ does not equal positive or negative infinity. Number 6 is an example of this.
::是的,只要不等于正或负的无限度,这是可能的。6号就是一个例子。

Section 15.3: Graphs to Find Limits
::第15.3节:确定限额的图表

$\begin{align*}\lim\limits_{x\to\text{-}\infty}{f(x)=0}\end{align*}$
::limx-f(x)=0

$\begin{align*}\lim\limits_{x\to\infty}{f(x)=DNE}\end{align*}$
::limxf(x) = DNE

$\begin{align*}\lim\limits_{x\to{2}}{f(x)=DNE}\end{align*}$
::limx%2f(x) = DNE

$\begin{align*}\lim\limits_{x\to{0}}{f(x)=1}\end{align*}$
::limx0f(x)=1

$\begin{align*}f(0) = 2\end{align*}$
::f(0)=2

$\begin{align*}f(2)=6\end{align*}$
::f(2)=6

$\begin{align*}\lim\limits_{x\to\text{-}\infty}{g(x)=DNE}\end{align*}$
::limx-g(x) = DNE

$\begin{align*}\lim\limits_{x\to\infty}{g(x)=1}\end{align*}$
::limxg( x)=1

$\begin{align*}\lim\limits_{x\to{2}}{g(x)} = \text{-}2\end{align*}$
::limx%2g(x)=-2

$\begin{align*}\lim\limits_{x\to{0}}{g(x)=DNE}\end{align*}$
::limx0g(x) = DNE

$\begin{align*}\lim\limits_{x\to{4}}{g(x)=0}\end{align*}$
::limx4g(x)=0

$\begin{align*}g(0)=2\end{align*}$
::g( 0)=2

$\begin{align*}g(2) = 4\end{align*}$
::g(2)=4

Answers vary.
::答案不尽相同。

Answers vary.
::答案不尽相同。

Section 15.4: Tables to Find Limits
::第15.4节:确定限额的表格

10

-5

DNE
::DNN DN DN

$\begin{align*}\tfrac{1}{2\sqrt{2}} \approx 0.35355\end{align*}$

DNE
::DNN DN DN

9

-6

$\begin{align*}\tfrac{1}{2\sqrt{5}} \approx 0.2236\end{align*}$

$\begin{align*}\tfrac{1}{6}\end{align*}$

5

-6

$\begin{align*}\tfrac{1}{4}\end{align*}$

$\begin{align*}\tfrac{1}{4}\end{align*}$

$\begin{align*}\tfrac{2}{15}\end{align*}$

DNE
::DNN DN DN

Section 15.5: Substitution to Find Limits
::第15.5节:用以确定限额的替代

10

-5

-7

$\begin{align*}\text{-}\tfrac{1}{5}\end{align*}$

3

9

-6

$\begin{align*}\text{-}\tfrac{1}{3}\end{align*}$

7

5

-6

DNE
::DNN DN DN

6

$\begin{align*}\tfrac{2}{15}\end{align*}$

DNE
::DNN DN DN

Section 15.6: Rationalization to Find Limits
::第15.6节:寻找限制的合理化

$\begin{align*}\tfrac{1}{6}\end{align*}$

$\begin{align*}\tfrac{1}{4}\end{align*}$

$\begin{align*}\tfrac{1}{4}\end{align*}$

$\begin{align*}\tfrac{1}{2\sqrt{3}}\end{align*}$

$\begin{align*}\tfrac{5}{8}\end{align*}$

$\begin{align*}\text{-}\tfrac{1}{4}\end{align*}$

$\begin{align*}\tfrac{1}{2\sqrt{7}}\end{align*}$

8

$\begin{align*}4\sqrt{3}\end{align*}$

$\begin{align*}\tfrac{1}{6}\end{align*}$

$\begin{align*}\tfrac{1}{2}\end{align*}$

2

64

-144

If the function is a rational expression with a square root somewhere, there is a good chance that rationalizing will help you to evaluate the limit.
::如果函数是某处带有平方根的合理表达式,那么理顺很有可能有助于您评估极限值。

Section 15.7: Continuity
::第15.7节:连续性

1

1

Yes
::是是

11

11

No, because $\begin{align*}g(\text{-}2) \ne 11\end{align*}$ .
::不,因为g(-2)\\\\\\\\\\\\\\\\\\\\\\\\\\

-3

-3

-2

No, because $\begin{align*}h(0) \ne \text{-}3\end{align*}$
::否,因为 h(0) {________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

Answers vary. Any continuous interval that does not include 0 should work.
::答复各有不同。任何连续间隔,如果不包括0,应该有效。

Answers vary. Possible answer: [-1, 1].
::答复不尽相同,可能的答复是[-1,1]。

Since $\begin{align*}\lim\limits_{x\to{\text{-}2^-}}{3x+1} = \text{-}5\end{align*}$ and $\begin{align*}\lim\limits_{x\to{\text{-}2^+}}{\text{-}2x-1} = 3,\end{align*}$ there is no value of $\begin{align*}k\end{align*}$ that makes the function continuous.
::由于 limx-2-3x+1=-5 和 limx-2+-2x-1=3, k 没有值使函数持续。

1

-3

Section 15.8: Intermediate and Extreme Value Theorems
::第15.8节:中间和极端价值理论

$\begin{align*}f(\text{-}1) = \cos{(\text{-}1)}-1 = \text{-}0.4596\end{align*}$ and $\begin{align*}f(1) = \cos{(1)}+1 = 1.54;\end{align*}$ therefore, there must exist a $\begin{align*}c\end{align*}$ such that $\begin{align*}f(c) = 0\end{align*}$ because $\begin{align*}\text{-}0.4596 < 0 < 1.54\end{align*}$ .
::f(-1)=cos(-1)-1=-0.4596和f(1)=cos(1)+1=1.54;因此,必须存在f(c)=0的c,因为 -0.4596 <0<1.54。

$\begin{align*}f(1) = ln(1) -e^{\text{-}1} - 1 = \text{-}1.37\end{align*}$ and $\begin{align*}f(3) = ln(3)-e^{\text{-}3}-1 = 0.4883;\end{align*}$ therefore, there must exist a $\begin{align*}c\end{align*}$ such that $\begin{align*}f(c) = 0\end{align*}$ because $\begin{align*}\text{-}1.37 < 0 < 0.4883\end{align*}$ .
::f(1)=ln(1)-e-1-1=-1.37和f(3)=ln(3)-e-3-1=0.4883;因此,必须存在f(c)=0的c,因为-1.37 <0.4883。

$\begin{align*}f(1) = 2(1)^3 - 5(1)^2 - 10(1)+5 = \text{-}8\end{align*}$ and $\begin{align*}f(0) = 2(0)^3 - 5(0)^2 -10(0)+5 = 5;\end{align*}$ therefore, there must exist a $\begin{align*}c\end{align*}$ such that $\begin{align*}f(c) = 0\end{align*}$ because $\begin{align*}\text{-}8 < 0 < 5\end{align*}$ .
::f(1)=2(1)3-5(1)-2-10(1)+5=8和f(0)=2(0)3-5(0)2-10(0)+5=5;因此,必须存在f(c)=0,因为 -8 <0 <5)

$\begin{align*}f(x) = x^3-x-1\end{align*}$ . $\begin{align*}f(0) = \text{-}1\end{align*}$ and $\begin{align*}f(2) = 5\end{align*}$ ; therefore, there must exist a $\begin{align*}c\end{align*}$ such that $\begin{align*}f(c) = 0\end{align*}$ because $\begin{align*}\text{-}1< 0 < 5\end{align*}$ .
::f( x) =x3- x- 1. f( 0) =-1 和 f(2)= 5; 因此, 必须存在这样的 c, 因为 - 1 < 0 < 5 , f( c) = 0 。

$\begin{align*}f(\text{-}2) = (\text{-}2)^2 - \cos{(\text{-}2)} = 4.4\end{align*}$ and $\begin{align*}f(0) = (0)^2 - \cos{(0)} = \text{-}1;\end{align*}$ therefore, there must exist a $\begin{align*}c\end{align*}$ such that $\begin{align*}f(c) = 0\end{align*}$ because $\begin{align*}\text{-}1 < 0 < 4.4\end{align*}$ .
::f( 2) = ( 2) 2 - cos( 2) = 4. 4 和 f( 0) = ( 0) 2 - cos( 0) =-1; 因此, 一定存在 f( c) = 0 因为 - 1 < 0 < 4. 4 。

$\begin{align*}f(x) = x^5 - 2x^3 -2\end{align*}$ . $\begin{align*}f(1) = \text{-}3\end{align*}$ and $\begin{align*}f(2) = 14\end{align*}$ ; therefore, there must exist a $\begin{align*}c\end{align*}$ such that $\begin{align*}f(c) = 0\end{align*}$ because $\begin{align*}\text{-}3 < 0 < 14\end{align*}$ .
::f(x) =x5-2x3-2. f(1)=-3 和 f(2)=14; 因此, 一定存在f(c)=0的 c, 因为 - 3 < 0 < 14 。

$\begin{align*}f(x) = 3x^2 + 4x - 11\end{align*}$ . $\begin{align*}f(1) = \text{-}4\end{align*}$ and $\begin{align*}f(2) = 9\end{align*}$ ; therefore, there must exist a $\begin{align*}c\end{align*}$ such that $\begin{align*}f(c) = 0\end{align*}$ because $\begin{align*}\text{-}4 < 0 < 9\end{align*}$ .
::f(x) = 3x2+4x- 11. f(1)= 4 和 f(2)= 9; 因此, 一定存在f(c)=0的 c, 因为 - 4 < 0 < 9 。

$\begin{align*}f(x) = 5x^4-6x^2-1\end{align*}$ . $\begin{align*}f(1) = \text{-}2\end{align*}$ and $\begin{align*}f(2) = 55\end{align*}$ ; therefore, there must exist a $\begin{align*}c\end{align*}$ such that $\begin{align*}f(c) = 0\end{align*}$ because $\begin{align*}\text{-}2 < 0 < 55\end{align*}$ .
::f(x) = 5x4-6x2- 1. f(1)= 2 和 f(2)= 55; 因此, 必须存在 f(c) = 0 因为 - 2 < 0 < 55 。

$\begin{align*}f(x) = 7x^3 - 18x^2 - 4x +1\end{align*}$ . $\begin{align*}f(\text{-}1) = \text{-}20\end{align*}$ and $\begin{align*}f(0)=1\end{align*}$ ; therefore, there must exist a $\begin{align*}c\end{align*}$ such that $\begin{align*}f(c) = 0\end{align*}$ because $\begin{align*}\text{-}20 < 0 < 1\end{align*}$ .
::f( x) = 7x3- 18x2- 4x+1. f(-1) =-20 和 f( 0)=1; 因此, 必须有 f( c) =0 的 c , 因为 -20 < 0 < 1 。

$\begin{align*}f(1) = \tfrac{1}{3}\end{align*}$ and $\begin{align*}f(2) = \text{-}1;\end{align*}$ therefore, there must exist a $\begin{align*}c\end{align*}$ such that $\begin{align*}f(c) = 0\end{align*}$ because $\begin{align*}\text{-}1 < 0 < \tfrac{1}{3}\end{align*}$ .
::f(1)=13和f(2)=1;因此,必须存在f(c)=0的c,因为 -1 <0 < 13。

$\begin{align*}f(\text{-}1) = \text{-}1\end{align*}$ and $\begin{align*}f(0) = \tfrac{1}{4};\end{align*}$ therefore, there must exist a $\begin{align*}c\end{align*}$ such that $\begin{align*}f(c) = 0\end{align*}$ because $\begin{align*}\text{-}1 < 0 < \tfrac{1}{4}\end{align*}$ .
::f(-1) =-1 和 f( 0) = 14; 因此, 必须存在 f( c) = 0 因为 - 1 < 0 < 14 。

False
::假假

True
::真实

True
::真实

Functions must be continuous over given intervals in order for the theorems to apply.
::功能必须是连续的,间隔一定的时间间隔内才能适用定理。

Section 15.9: Instantaneous Rate of Change
::第15.9节:即时变化率

The slope appears to be 2.
::斜坡似乎为2。

The limit is 2, which is the same as what the slope appeared to be in Number 1.
::限值是2, 与1号的斜坡相同。

The slope appears to be 6.
::斜坡似乎为6。

The limit is 6, which is the same as what the slope appeared to be in Number 3.
::限值是6, 与第3页的斜坡相同。

The slope appears to be 3.
::斜坡似乎为3。

The limit is 3, which is the same as what the slope appeared to be in Number 5.
::限值是3, 与5号山坡看起来相同。

The slope appears to be 6.
::斜坡似乎为6。

$\begin{align*}\lim\limits_{x\to{1}}{\left(\tfrac{2x^3-1-1}{x-1}\right)}\end{align*}$
::limx%1( 2x3 - 1 - 1 - 1x- 1)

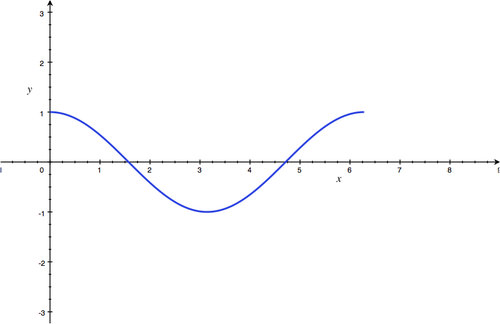
The slope at 0 is 0. The slope at $\begin{align*}\tfrac{\pi}{2}\end{align*}$ is -1. The slope at $\begin{align*}\pi\end{align*}$ is 0. The slope at $\begin{align*}\tfrac{3\pi}{2}\end{align*}$ is 1. The slope at $\begin{align*}2\pi\end{align*}$ is 0.

::0为0。% 2 的斜度为 - 1. = 0。% 2 的斜度为 1 。% 2 的斜度为 0 。% 2 的斜度为 1 。

The derivative of the cosine function is the negative sine function.
::余弦函数的衍生物是负正弦函数。

The slope is 2 at every point. The derivative of the function is $\begin{align*}y=2\end{align*}$ .
::每个点的斜坡为 2。函数的衍生值为 Y= 2 。

Distance vs. Time

Rate vs. Time

::距离对时间率对时间

A tangent line is a line that "just touches" a curve. The slope of the tangent line at a given point is the derivative of the function at that point.
::正切线是“ 碰触” 曲线的线条。相切线的斜度在给定点是函数在那个点的衍生物。

Instantaneous rate of change is the speed at a given point. Speed is shown as slope in functions; therefore, the slope of the tangent line will be the speed or instantaneous rate of change at that point.
::瞬间变化速度是某一点的速度。速度以函数的斜度显示;因此,正切线的斜度将是该点的速率或瞬时变化速度。

We can't calculate a slope with a denominator of 0, but we can use limits to find the limit of the slope as the denominator approaches 0.
::我们无法计算一个分母为0的斜坡, 但我们可以用极限来找到斜坡的极限, 当分母接近0时。

Section 15.10: Area Under a Curve
::第15.10节:曲线下区域

176

60

8.79

8.86

-0.33

-0.59

-0.72

The car is going at a constant speed of 25 mph for 3 hours, and then instantly starts going 65 mph for the next 2 hours.
::汽车在3小时内以25英里的恒定速度行驶, 3个小时, 然后在接下来的2个小时里, 立即开始开往65英里的行驶。

205 miles
::205英里

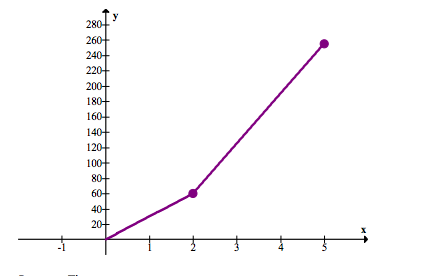
The car accelerates steadily from 0 to 75 meters per second in the first 3 seconds, and then stays at 75 meters per second for the next 2 seconds.
::汽车在前3秒内从每秒0米稳步加速到75米,然后在接下来的2秒内停留在每秒75米。

262.5 feet
::262.5英尺

The runner increases in speed from 0 feet per second to 16 feet per second, then slows back down to 0 feet per second.
::跑者的速度从每秒0英尺增加到每秒16英尺,然后减慢到每秒0英尺。

The exact answer is $\begin{align*}\tfrac{256}{3} \approx 85.33\end{align*}$ .
::确切答案是256385.33。

Integrals are areas under a curve. They can be calculated by finding the sum of the areas of an infinite number of rectangles.
::元件是曲线下的区域,可以通过找到无数矩形的区域的总和来计算。

章节大纲

Section 15.2: Limit Notation ::第15.2节:限制说明

Section 15.3: Graphs to Find Limits ::第15.3节:确定限额的图表

Section 15.4: Tables to Find Limits ::第15.4节:确定限额的表格

Section 15.5: Substitution to Find Limits ::第15.5节:用以确定限额的替代

Section 15.6: Rationalization to Find Limits ::第15.6节:寻找限制的合理化

Section 15.7: Continuity ::第15.7节:连续性

Section 15.8: Intermediate and Extreme Value Theorems ::第15.8节:中间和极端价值理论

Section 15.9: Instantaneous Rate of Change ::第15.9节:即时变化率

Section 15.10: Area Under a Curve ::第15.10节:曲线下区域

Section 15.2: Limit Notation
::第15.2节:限制说明

Section 15.3: Graphs to Find Limits
::第15.3节:确定限额的图表

Section 15.4: Tables to Find Limits
::第15.4节:确定限额的表格

Section 15.5: Substitution to Find Limits
::第15.5节:用以确定限额的替代

Section 15.6: Rationalization to Find Limits
::第15.6节:寻找限制的合理化

Section 15.7: Continuity
::第15.7节:连续性

Section 15.8: Intermediate and Extreme Value Theorems
::第15.8节:中间和极端价值理论

Section 15.9: Instantaneous Rate of Change
::第15.9节:即时变化率

Section 15.10: Area Under a Curve
::第15.10节:曲线下区域