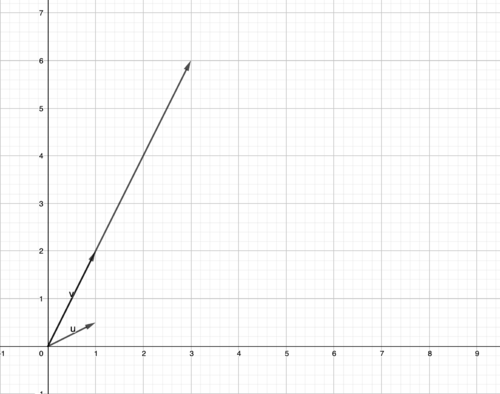Section: 矢量、长度和方向 | 1.1 矢量、长度和方向

Section outline

A vector is a mathematical object with both length and direction. It is written as a coordinate and represented as an arrow, like a point. We see here:
::矢量是一个具有长度和方向的数学对象。它是写成坐标和箭头,像点。我们在这里看到:

Vectors can be manipulated just like numbers can.
::矢量可以被操纵就像数字一样

The sum of two vectors is defined as summing both entries. We can find the vector $\begin{align*}\vec{u}+\vec{v}\end{align*}$ where we get $\begin{align*}\vec{u}=\begin{bmatrix}u_{1}\\u_{2}\end{bmatrix}\end{align*}$ and $\begin{align*}\vec{v}=\begin{bmatrix}v_{1}\\v_{2}\end{bmatrix}\end{align*}$ and those end up summing to $\begin{align*}\overrightarrow{u+v}=\begin{bmatrix}u_{1}+v_{1}\\u_{2}+v_{2}\end{bmatrix}\end{align*}$ .
::两个矢量的总和被定义为对两个条目进行折射。我们可以找到矢量 u=[u1u2] 和v=[v1v2] ,而最终的矢量为 +v=[u1+v1u2+v2] 。

We can also multiply vectors by scalars. We also do this by each entry wise as taking $\begin{align*}\vec{v}=\begin{bmatrix}v_{1}\\v_{2}\end{bmatrix}\end{align*}$
::我们也可以通过 scalar 来增加矢量。我们也可以通过每个输入来做此操作, 以“ v” = [v1v2] 来计算。

and multiplying by a scalar gives us $\begin{align*}c\cdot\vec{v}=\begin{bmatrix}c\cdot v_{1}\\c\cdot v_{2}\end{bmatrix}\end{align*}$
::乘以一个卡路里给了我们Cv=[cv1cv2]

Vectors can also occupy $\begin{align*}n\end{align*}$ points in $\begin{align*}n\end{align*}$ -dimensional space where each entry has real coordinates .
::矢量还可以占据正维空间的n点,每个入口都有真正的坐标。

Let’s try adding and multiplying a couple of vectors. While this is just simply simple multiplication and addition we will try to put a geometric spin on this by looking at what happens to the vectors when we apply these operations.
::让我们尝试增加和乘以几个矢量。虽然这只是简单的乘法和加法,但我们将尝试通过查看当我们应用这些操作时矢量发生的情况来对此进行几何旋转。

Our example will be $\begin{align*}3\cdot\begin{bmatrix}1\\2\end{bmatrix}+4\cdot\begin{bmatrix}1\\\frac{1}{2}\end{bmatrix}\end{align*}$
::我们的例例是3[12]+4[112]

You obviously know that we will get our final vector $\begin{align*}\vec{v}\end{align*}$ to be equivalent to and written as $\begin{align*}\vec{v}=\begin{bmatrix}7\\8\end{bmatrix}\end{align*}$ , but let's just look at the steps to see the geometric progression of this linear combination .
::您显然知道,我们将会把最终的矢量"v" 等同于和写成"v=[78], 但是让我们看看这些步骤来观察这个线性组合的几何进化。

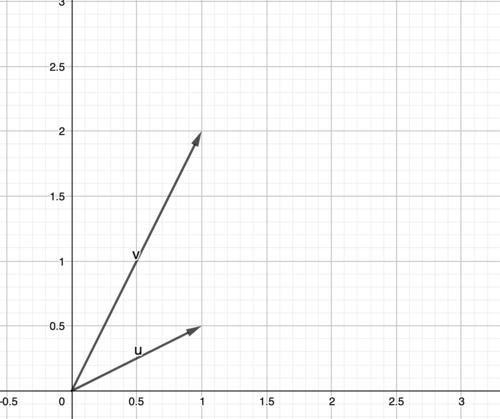
First we get $\begin{align*}u \text{ and } v\end{align*}$

::我们先得到你和你

Now we take $\begin{align*}3v \text{ and } u\end{align*}$

::现在,我们采取3v和u

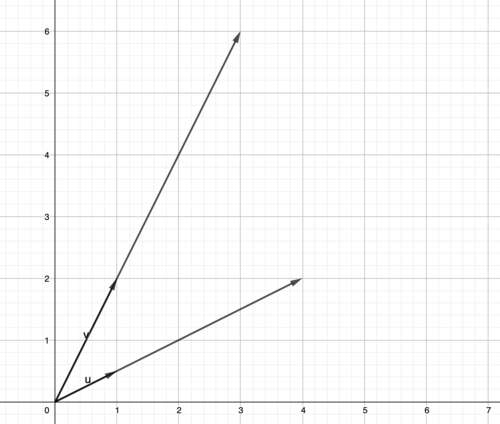
Then we multiply $\begin{align*}u\end{align*}$ by 4

::然后我们乘以 u 乘以 4

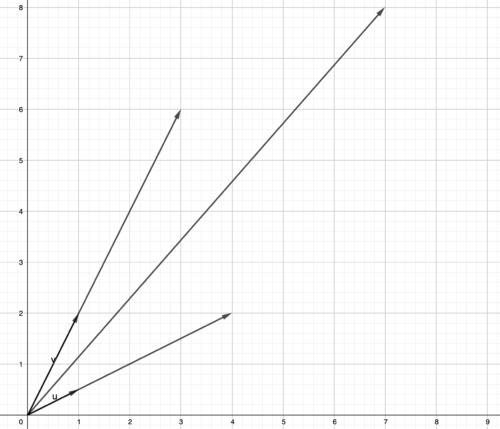
And lastly we sum component-wise to get $\begin{align*}4\begin{bmatrix}1\\\frac{1}{2}\end{bmatrix} + 3\begin{bmatrix}1\\2\end{bmatrix}\end{align*}$ :

::最后,我们把部件加起来以获得4[112]+3[12]:

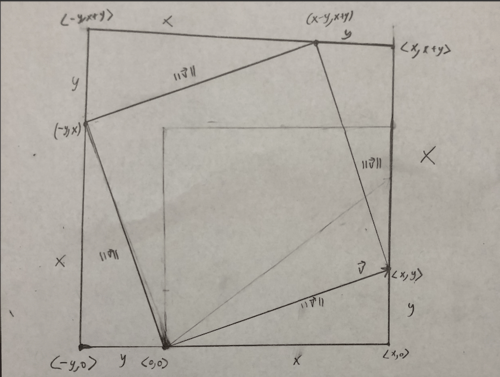
Now we can look at length or magnitude of a vector. From precalculus you probably know about the distance formula and pythagorean theorem so we can define magnitude of a vector that way.

Definition: Magnitude of a Vector

$\begin{align*}d(p_{1},p_{2}) := \sqrt{\sum_{i} ({p_{1}}_{i} - {p_{2}}_{i})^2}\end{align*}$ is the distance between two points where we are just squaring the differences between each entry assuming that $\begin{align*}p_{1} \text{ and } p_{2}\end{align*}$ are in the same dimension. Thus the magnitude of a vector is just the distance formula where one of the points is the origin and we take the square root of the sum of the squares of the entries expressed yielding $\begin{align*}||\vec{v}|| = \sqrt{\sum_{i} x_{i}^{2}}\end{align*}$ .

In two dimensional and three dimensional space the magnitude of $\begin{align*}\vec{v}\end{align*}$ is just $\begin{align*}||\vec{v}|| = \sqrt{x^{2}+y^{2}} \text{ or } ||\vec{v}|| = \sqrt{x^{2}+y^{2}+z^{2}}\end{align*}$ .

We can prove this for 2 dimensions in a geometric way:

Proof of the magnitude of a vector formula in 2 dimensions:

Looking at this photo we have taken our vector $\begin{align*}\vec{v}\end{align*}$ and rotated it into a square of side lengths as the magnitude of $\begin{align*}\vec{v}\end{align*}$ where we then encapsulate that inside another square with side lengths $\begin{align*}x+y\end{align*}$ which are the entries of our vector.
::看着这张照片,我们拍摄了我们的矢量 v 并把它旋转成平方形的侧长, 以等于 v 的大小, 然后我们将它封装在另一个正方形内, 侧长 x+y 是矢量的条目。

Now the area of the larger square can be expressed in two different ways where $\begin{align*}(x+y)^{2} = 4(\frac{x\cdot y}{2}) + ||\vec{v}||^{2} \end{align*}$ as we have the area is the side length squared and also the area of the smaller square plus the four right triangles.
::现在,大方的面积可以用两种不同的方式表示,即(x+y)2=4(xy2)v2,因为我们的面积是侧长平方,小方的面积加上四个右三角。

Now we simplify this to get $\begin{align*}x^{2}+2xy+y^{2} = 2xy + ||\vec{v}||^{2}\end{align*}$ thus subtracting out $\begin{align*}2xy\end{align*}$ from both sides we get that $\begin{align*}x^{2}+y^{2} = ||\vec{v}||^{2}\end{align*}$ thus we have proven our formula for the magnitude of a vector in two dimensions.
::现在我们简化此选项, 以获得 x2+2xy+y2=2xyv2, 从而从两侧减去 2xy, 我们得到的 x2+y2+y2v2, 因此我们证明了我们对于两个维度矢量的大小的公式。

We can see some similar proofs for higher-dimensions, but are less intuitive as the geometry is harder to visualize in dimensions above three.
::我们可以看到一些相似的证据来证明高分层, 但却不那么直观, 因为几何在三维以上更难想象。

Now let's look at some more identities!
::现在让我们看看更多的身份!

$\begin{align*}||k\cdot\vec{x}|| = |k|\cdot||\vec{x}||\end{align*}$
::{\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}我... {\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}我... {\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}

$\begin{align*}||\vec{x} + \vec{y}|| \leq ||\vec{x}|| + ||\vec{y}||\end{align*}$
::~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~

$\begin{align*} ||\vec{x}|| - ||\vec{y}|| \leq ||\vec{x} - \vec{y}|| \end{align*}$
::~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~

$\begin{align*}||\vec{x}||\cdot||\vec{y}||\cdot cos(\alpha) \leq ||\vec{x}|||\cdot||\vec{y}|| \text{ where $\alpha$ is the angle between the two vectors. }\end{align*}$
::

These identities are very useful when dealing with vectors, but we won't prove them until later in the chapter.
::这些身份在处理向量时非常有用但我们要等到章节后面才能证明

Direction of a vector
::矢量方向

From basic high school math you probably remember your trigonometric identities and acronyms like SOH-CAH-TOA.
::从基础高中数学中你可能记得你的三角特征和首字母缩写,如SOH -CAH -TOA

Just to review given a right triangle and a non-right angle $\begin{align*}\theta\end{align*}$ you get that the sine of $\begin{align*}\theta\end{align*}$ written as $\begin{align*}\text{sin}(\theta)\end{align*}$ is the opposite side divided by the hypotenuse and the cosine is the adjacent over the hypotenuse whereas the tangent is the ratio of the opposite over the adjacent side.
::仅审查一个右三角和一个非右角度 =========================================================================================================================================================================================== =======================================================================================================================================================================================================================================================================================================================

This is relavent to vectors because, while they just seem like an arrow in space you can depict them as right triangles, as seen here:
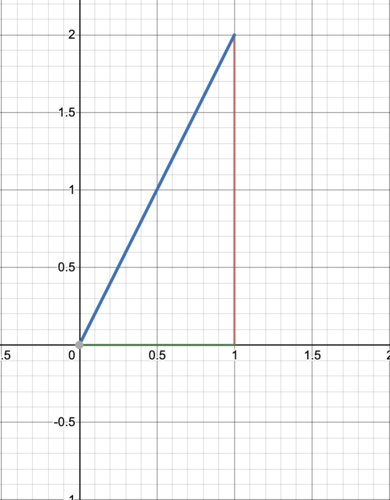
::这是矢量的惯性因为,虽然它们看起来只是太空中的箭头你可以把它们描绘成右三角形, 这里可以看到:

As you can see the blue line is the vector $\begin{align*}\vec{v} = \begin{bmatrix}1 \\ 2\end{bmatrix}\end{align*}$ . You should draw this as a right triangle and get that the angle we will call $\begin{align*}\theta\end{align*}$ is the angle between the vector and the axis and the goal when dealing with vectors, in some cases, will be to find an unknown value.
::您可以看到, 蓝线是矢量 v=[ 12]。您应该将此画成一个右三角形, 并且将我们称为的角作为矢量与轴之间的角, 而在某些情况下, 处理矢量时的目标将是找到未知值。

To do many of these tasks you have be familiar with SOH-CAH-TOA and the idea of length we went over earlier in this lesson.
::为了完成许多这些任务,你已经熟悉SOH-CAH-TOA和我们先前在教训中谈到的长度概念。

When given the coordinates of a vector $\begin{align*}\vec{x} = \begin{bmatrix}x_{1}\\x_{2}\end{bmatrix}\end{align*}$ and are asked to find the direction you should make the connection to the right triangle and remember that $\begin{align*}x_{1}\text{ is just adjacent side and }x_{2}\text{ is just the opposite. } \end{align*}$
::当给定矢量%x=[x1x2]的坐标, 并被要求找到方向时, 您应该将方向与右三角形连接, 并记住 x1 只是相邻的一面, 而 x2 就是相反的一面。

From this you see that $\begin{align*}\text{tan}(\theta) = \frac{x_{2}}{x_{1}}\end{align*}$ making the direction of your vector $\begin{align*}\text{arctan}(\frac{x_{2}}{x_{1}})\end{align*}$ where arctan is the inverse tangent function you learned about in trigonometry.
::从此您可以看到 tan =x2x1 正在向矢量 arctan( x2x1) 方向方向, 弧tan 是您在三角测量中学习的反正切函数。

Now given the magnitude and direction of a vector you may be asked to find the coordinates so just recall that the magnitude is just the hypotenuse length and that $\begin{align*}\vec{v} = \begin{bmatrix}||\vec{v}||\text{cos}(\theta)\\||\vec{v}||\text{sin}(\theta)\end{bmatrix}\end{align*}$ . This can also be derived from the basic identity that $\begin{align*}\text{sin}^{2}(\theta) + \text{cos}^{2}(\theta) = 1 \text{ for all angles }\theta\end{align*}$ . So $\begin{align*}||\vec{v}|| = \sqrt{||\vec{v}||^{2}\text{sin}^{2}(\theta) + ||\vec{v}||^{2}\text{cos}^{2}(\theta)} = \sqrt{||\vec{v}||^{2}} = ||\vec{v}||\end{align*}$ .
::现在,鉴于矢量的大小和方向, 您可以被请求找到坐标, 只需提醒您, 星值只是下限长度, 并且“ ” = [vcos vv sin] 。这也可以从所有角度的 sin2 +cos2 = 1 的基本特性来推断。所以“ vvv2sin2 v2vv2vvvv 。 ”

This video is a lot longer but does give many examples in case you are still unsure about the content: