Section: 分配和保理 | 2.4 分配和保理-interactive

Section outline

The Purpose of this Lesson
::本课程的目的

In this lesson, you will explore the area of rectangles and use the to multiply two binomials. You'll reverse the process to factor quadratic expressions.
::在此课中, 您将探索矩形区域, 并使用矩形来乘以两个二元论。您将颠倒进程, 以因子矩形表达式。

Activity 1 : Distribution by Calculating the Area of a Square

::活动1:通过计算广场面积进行分配

Example 1-1
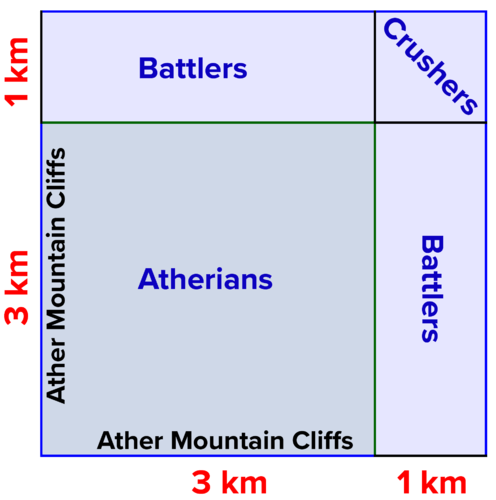
::例1-1

In the mythological mountains of Ather , a queen rules a small city. The city is a perfect square , 3 kilometers on a side. On two sides, the city is bordered by great cliffs from which the queen launches her dragons in case of attack. The other two sides are vulnerable, and the queen decides to populate these sides with trained Battlers and Crushers . She will extend the city exactly 1 kilometer on each side, as shown below. The Battlers will occupy the rectangular regions, and the Crushers the small square, with the rest of the regular untrained citizens, Atherians, living in the larger square.
::在神话般的阿特尔山上,女王统治着一座小城市。城市是一个完美的广场,一面3公里。在两边,城市被大悬崖所包围,女王在进攻时从那里发射龙头。另外两边是脆弱的,女王决定用训练有素的战士和粉碎者把两边围成一片。她将每边一公里的城扩张,如下文所示。战斗者将占领长方形地区,粉碎小广场,其余未受过训练的公民阿特赫里亚人则住在大广场。

What is the area of each region?
::每个区域的面积是多少?

What is the new area of the entire city?
::整个城市的新区域是什么?

The city is 3 km on each side, and is protected by cliffs on two sides. The Battlers and Crushers are arrayed to guard the sides away from the cliffs.

Solution:
::解决方案 :

$\begin{aligned} \begin{array}{lll} Occupants & Area ({km}^{2}) & Description \\ Atherians & 3^{2} = 9 & The larger of the two squares. \\ Battlers & 1 \cdot 3 + 3 \cdot 1 = 6 & The two rectangles. \\ Crushers & 1 \cdot 1 = 1 & The smaller square. \end{array} \end{aligned}$

::OccupantsArea( km2) 描述Atherians32=9 两个方形中较大方形。工具13+31=6 两个矩形。 Crushers11=1 小方形。

The total area is $\begin{aligned} 9 + 6 + 1 = 16 {km}^{2} . \end{aligned}$ This can also be found by observing that the entire figure is a 4 by 4 square, whose area is $\begin{aligned} 4 \cdot 4 = 16 {km}^{2} . \end{aligned}$
::总面积为9+6+1=16平方公里,这也可以通过观察到整个数字是4+4平方公里,面积为4+4=16平方公里。

Work it Out
::工作出来

A decade passes peacefully and gradually. T he Atherians, Battlers, and Crushers mingle and relax such that the city is just a large square of Atherians. The queen notices that the city is as defenseless as before, but larger, so she decides to extend the perimeter again by adding 1 kilometer to each side as before. Sketch the plan and find the area of each region. How much has the Atherian area increased? The Battler area? The Crusher area?
::十年和平而缓慢地过去了。阿特赫里亚人、作战者、粉碎者们聚集在一起,放松下来,使这座城市仅仅是一个大面积的阿特赫里亚人广场。女王们注意到,该城市和以前一样无防御能力,但规模更大,因此她决定把周界再扩大一公里,每边都增加一公里。绘制计划,找到每个地区的面积。亚特里亚人地区增加了多少?战斗者地区?碎石区?

Extend the perimeter by extending the sides again. Look at the increases in the area of each region. Describe the patterns you observe.
::延长周界,再扩展两侧。看看每个地区面积的增加,描述你观察到的规律。

Interactive
::交互式互动

A prince visits the queen and tells the tale of many cities that wish to expand like hers. He wants to know: if a city is a square with dimensions $\begin{aligned} x \end{aligned}$ by $\begin{aligned} x \end{aligned}$ , and it extends its dimensions by 1 kilometer, are there algebraic expressions for the area of the Atherian, Battler, and Crusher regions? What is the resulting area of the entire expanded city?
::一位王子拜访女王,讲述了许多城市的故事,这些城市希望像她一样扩张。他想知道:如果一个城市是一个面积为xxxx的正方形,其面积扩大1公里,那么Atherian、Battler和Crusher地区是否有代数表达方式?整个扩张城市的面积为何?

Use the interactive below to help visualize this problem. Move the red point to change the size of the city sections.
::使用下面的交互效果来帮助直观地看到这个问题。移动红点以改变城市区块的大小。

INTERACTIVE

Changing the City

Move the red point to change the size of the city sections.
::移动红点以更改城市区块的大小。

Your device seems to be offline.
Please check your internet connection and try again.

+

Do you want to reset the PLIX?

Yes

No

Example 1-2
::例1-2

From the last problem, the expression for the entire area of an expanded city is:
::从最后一个问题来看, 城市扩张的整个地区的表达方式是:

$\begin{aligned} x^{2} + 2 x + 1 \end{aligned}$

::x2+2x+1

Find another way to express the entire area of the expanded city.
::寻找另一种方式来表达整个城市的面积。

Solution: You can also find the area of the expanded city by squaring the length of one side:
::解决方案:您也可以通过划分一面的长度找到扩张城市的面积:

These two expressions of the expanded area are equivalent:
::扩大面积的这两个表达方式相同:

$\begin{aligned} (x + 1)^{2} = x^{2} + 2 x + 1 \end{aligned}$

:x+1)2=x2+2x+1

In fact, you call the right-hand expression the expanded form of the left-hand expression. The left-hand form is the factored form because it's written as expressions which multiply to the same result:
::事实上,您将右手表达式称为左手表达式的扩展形式。左手表达式是因数表达式,因为它作为表达式写成,乘以同一结果:

$\begin{aligned} \begin{array}{ll} Factored Form & Expanded Form \\ (x + 1)^{2} & x^{2} + 2 x + 1 \\ (x + 1) (x + 1) & x^{2} + 2 x + 1 \end{array} \end{aligned}$

::系数化窗体扩展窗体 (x+1) 2x2+2x+1(x+1)(x+1)(x+1) x2+2x+1

Factored Form vs. Expanded Form for a Polynomial
::乘数表对多面体扩大表

A polynomial is in factored form if it is written as a product of .
::多面性如果是作为...的产物写成的,则以系数表示。

A polynomial is in expanded form if it is written as a sum of terms .
::如果多语种以一言一行的形式写成,则以扩大的形式出现。

Interactive
::交互式互动

The queen suggests that some cities may wish to extend the dimensions by more than 1 kilometer. Use the following interactive to visualize these options.
::女王建议一些城市可能希望将尺寸扩大1公里以上。使用以下互动方式将这些选项直观化。

Express the area of each expanded city in the interactive, both in factored form and in expanded form.
::以因素形式和扩展形式以互动形式表达每个扩大的城市的面积。

Generalize your results. Find the area in expanded form of a square city with side length $\begin{aligned} x + b . \end{aligned}$
::将您的结果概括化。找到以面积扩大的平方城市形式、侧长 x+b 的区域。

INTERACTIVE

Squaring Binomials

Use the interactive below to help visualize this problem.
::使用下面的交互效果来帮助直观地看待这个问题。

Move the red and blue points to change the size of the city sections.
::移动红点和蓝色点以改变城市区块的大小。

Your device seems to be offline.
Please check your internet connection and try again.

+

Do you want to reset the PLIX?

Yes

No

Activity 2: Distribute by Calculating Area of a Rectangle
::活动2:通过矩形的计算区域进行分布

Interactive
::交互式互动

The queen realizes that some cities may want more battlers on one side than the other. Use this interactive to explore these options.
::皇后意识到有些城市可能比另一个城市需要更多战斗者。使用此互动来探索这些选项。

Express the area of each expanded city in the interactive, both in factored form and expanded form.

::以因素形式和扩展形式以互动形式表达每个扩大城市的面积。

Generalize your results. Find the area in expanded form of a rectangular city with dimensions $\begin{aligned} x + b \end{aligned}$ by $\begin{aligned} x + t . \end{aligned}$
::将您的结果一般化。以长方形城市的扩展形式查找区域, 其尺寸 x+b 乘 x+t 。

INTERACTIVE

Multiplying Binomials

Move the red, blue, and green points to change the size of the city sections.
::移动红色、蓝色和绿色点以改变城市区域的大小。

Your device seems to be offline.
Please check your internet connection and try again.

+

Do you want to reset the PLIX?

Yes

No

Activity 3: Factoring Given Area of Regions
::活动3:按特定区域确定区域因素

Example 3-1
::例3-1

The land of Ather also features nomadic tribes who seek to settle down to form rectangular cities like the ones you've explored so far. These tribes have Atherians, Battlers, and Crushers. Below is a table showing the area that Atherians, Battlers, and Crushers would occupy for each tribe. Make a rectangular city for each tribe to occupy, with the appropriate regions for Atherians, Battlers, and Crushers. Once you find the dimensions of the city, confirm your results are correct by finding the area of the entire city by multiplying its overall dimensions.
::阿他的地也具有游牧部落的特征、他们寻求定居、形成像你所探寻的长形城 . 这些部落有亞太人、战士、和粉碎人 . 下面的桌子、表明亞他人、战士、和碎人所占领的地、各部落所占领的地、和亞他人、战兵、和碎人所居住的地。一旦发现城的方位、和碎碎人所的地、、你所所得的地、你所的、你所得的地、你的地、你、你所的、你所、你所得的的的地、你、你所都是的的、你都是的、你的的、你都是的的、你、你都是都是的的的、都是的的、都是的、是的的、是的的、是、是、是的的的的的、是、是的的的的的的的、、、是的的、是、是的的、是的的的、是、是的的的、是、是、是、是的的的、是、是、是的、是的的的的的的、是的的、是、是的的的、是的的、是、是的的的的、是的、是的、

$\begin{aligned} \begin{array}{ccc} Atherians & Battlers & Crushers \\ 9 & 6 & 1 \\ 25 & 25 & 6 \\ 49 & 21 & 2 \end{array} \end{aligned}$

::冲压器 9612525649212

Solution: A general strategy to finding the dimensions is given below.
::解决办法:下面是寻找这些层面的总战略。

Note that the Atherian area fills a square. So in each case, the dimensions of the square are the square root of the value.
::请注意, Atherian 区域填充一个方形。所以在每种情况下, 方形的尺寸都是值的平方根。

The Battlers are split into two different rectangles, and since it's not clear how to split them, move on to the Crushers.
::战斗者被分成两个不同的矩形, 并且由于不清楚如何分割它们, 继续前进到毁灭者。

The Crushers fill a single rectangle, so if you factor their area, you get some options for how to complete the overall rectangle.
::Crushers 填充一个单一的矩形, 所以,如果你考虑到他们的区域, 你就会得到一些选择, 来完成整个矩形。

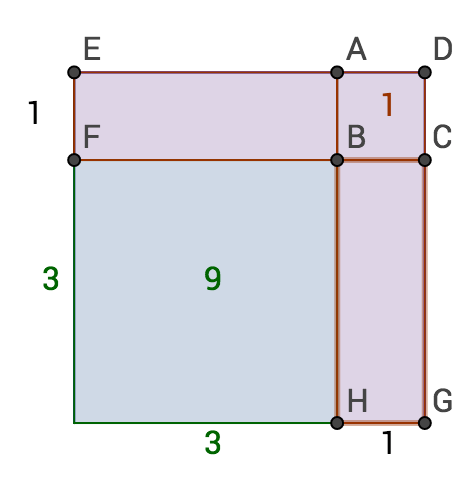
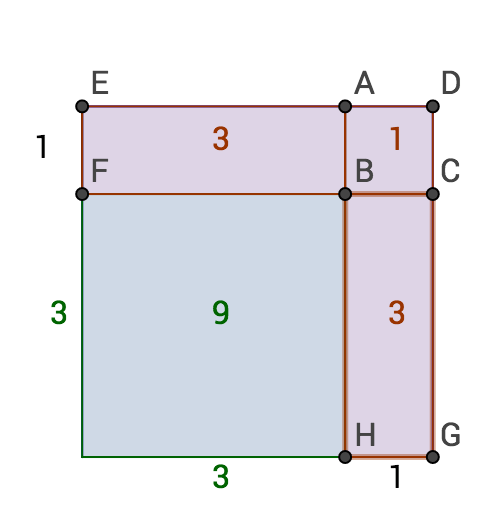
Consider 9,6,1 first. The Atherian square must be 3 by 3, and the Crushers 1 by 1:
::先考虑9,6,1,Atherian广场必须是3比3,1是粉碎者1比1:

<

Completing the Battler area gives:
::完成战斗区域时给出 :

The Battler area is 6, as hoped. The area of the entire city is $\begin{aligned} 4 \cdot 4 = 16 \end{aligned}$ , which equals the sum of the given regions, 9,6, and 1.
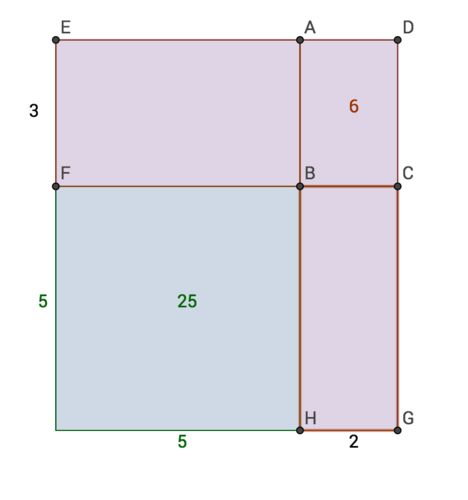
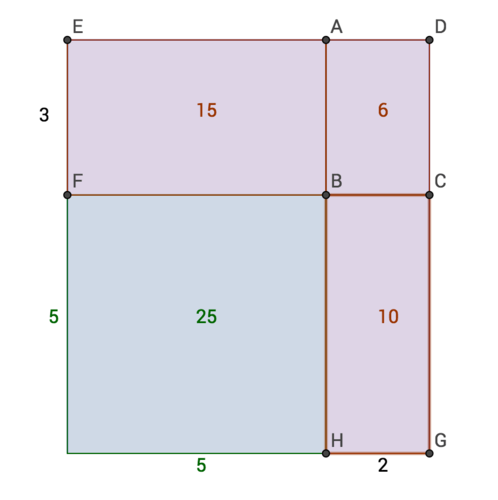
Now take 25,25,6. The large square is 5 by 5, and the small square could be either 6 by 1 or 2 by 3. If you try with 6 by 1, the Battler area doesn't end up correct. So try 2 by 3:
::战斗区是6个, 整个城市的面积是44=16, 相当于给定区域的总和, 9, 6, 和 1, 现在需要2525, 256。大广场是5乘5, 小广场可以是6乘1或2乘3, 如果尝试6乘1, 战斗区是错的。所以尝试2乘3:

Completing the Battler area gives:
::完成战斗区域时给出 :

The Battler area is 25, as hoped. The area of the entire city is $\begin{aligned} 8 \cdot 7 = 56 \end{aligned}$ , which equals the sum of the given regions, 25, 25, and 6.
::战斗区如所希望的那样为25个,整个城市面积为8+7=56,相当于特定地区(25、25和6)的总和。

Work it Out
::工作出来

Below is a table showing the area that Atherians, Battlers, and Crushers would occupy for several tribes. Make a rectangular city for each tribe to occupy, with the appropriate regions for Atherians, Battlers, and Crushers. Once you find the dimensions of the city, confirm your results are correct by finding the area of the entire city by multiplying its overall dimensions.
::下面的一张表格显示了阿特赫里亚人、作战者和粉碎者将占据几个部落的地区。为每个部落建造一座长方形城市,为阿特赫里亚人、作战者和粉碎者提供适当的区域。一旦你发现了城市的方位,通过将整个城市的面积乘以其整体尺寸来确认你的结果是正确的。

$\begin{aligned} \begin{array}{ccc} Atherians & Battlers & Crushers \\ 81 & 18 & 1 \\ 16 & 32 & 15 \\ 36 & 18 & 2 \end{array} \end{aligned}$

::冲压器 8118116321536182

Interactive
::交互式互动

Use the interactive to try factoring quadratic expressions using algebra tiles.
::使用交互式来尝试用代数瓦来乘以二次表达式。

INTERACTIVE

Boxes for Factoring

Use the boxes to figure out the factors of the polynomial on the top
::使用框来解析顶部的多数值系数

Input the factors into the input boxes
::将系数输入输入框

Your device seems to be offline.
Please check your internet connection and try again.

+

Do you want to reset the PLIX?

Yes

No

Activity 4: Factoring Quadratic Expressions
::活动4:计算二次曲线表达式

Recall that an area model can be used to expand a quadratic expression from factored form, $\begin{aligned} (x + p) (x + q), \end{aligned}$ to standard (or expanded) form, $\begin{aligned} a x^{2} + b x + c . \end{aligned}$
::回顾区域模型可用于将二次表达式从因数表(x+p)(x+q)扩展至标准(或扩展)表、x2+bx+c。

Notice how (1) the product of the diagonals are equal, $\begin{aligned} (6 x^{2}) (- 20) = - 120 x^{2} and (- 8 x) (15 x) = - 120 x^{2} \end{aligned}$ and (2) the sum of the $\begin{aligned} x \end{aligned}$ -terms equal the linear term , $\begin{aligned} - 8 x + 15 x = 7 x . \end{aligned}$
::注意 (1) 对角线的产物是相等的, (6x2)(-20) 120x2 和 (-8x)(15x) 120x2 和 (2) x- 期的总和等于线性术语, 即 - 8x+15x= 7x 。

Factor Using Area Models
::使用面积模型的因数

Area models can also be used to factor quadratic expressions in standard form . The quadratic term and constant term always go in the bottom -left and top -right squares of the area model.
::也可以使用区域模型来计算标准形式的二次表达式。二次词和恒定词总是在区域模型的下左方和右上方方。

T he linear term, however, is split between the top -left and bottom -right squares. Two key ideas from area models that will help us figure out how to split up the linear term are:
::然而,线性术语在左上方和右下方方之间分割。区域模型中的两个关键想法将帮助我们找出如何将线性术语分割开来:

The product of the diagonals are equal.
::对角体的产物是平等的。

The sum of the $\begin{aligned} x \end{aligned}$ -terms equals the linear term.
::x条件总和等于线性术语。

So the blue squares must multiply to $\begin{aligned} a x^{2} \cdot c \end{aligned}$ and add to $\begin{aligned} b x . \end{aligned}$ One way to organize this information is by setting up an X problem, as shown below. The sides of the X will be the two terms that add to the top and multiply to the bottom.
::因此蓝色方块必须乘以 x2c 并添加到 bx。组织此信息的一种方法是设置 X 问题, 如下文所示。 X 的两边是两个词, 向上加到和向下加到两个词。

Using the Area Model to Factor a Quadratic Expression
::使用“区域模型”来乘以二次曲线表达式

To rewrite a quadratic expression from standard form, $\begin{aligned} a x^{2} + b x + c, \end{aligned}$ to factored form, $\begin{aligned} (x + p) (x + q) : \end{aligned}$
::重写一个二次表达式,从标准格式x2+bx+c, 重写成因数表达式, (x+p)(x+q):

Draw a 2 by 2 area model. Fill in the of the bottom - left with the quadratic term $\begin{aligned} (a x^{2}) \end{aligned}$ and the top - right with the constant term $\begin{aligned} (c) . \end{aligned}$
::绘制 2 乘 2 区域模型。填充左下角, 填充方字( 轴) , 填充右上角, 填充常数( c) 。

Draw a large X . W rite the linear term $\begin{aligned} (b x) \end{aligned}$ on the top and the product of the quadratic and constant term $\begin{aligned} (a x^{2} \cdot c) \end{aligned}$ on the bottom of the X .
::绘制大 X。在 X 的顶部写线性术语(bx), 在 X 的底部写成二次和常数术语( 轴2c) 的产物。

In the sides of the X , find two terms that will add to the top and multiply to the bottom .
::在X的两侧找到两个词增加到顶部增加到底部

F ill in the top- left and bottom- right of the area model with the terms you found in Step 3 .
::填充区域模型的左上角和右下角,填写步骤3中的条件。

Write the greatest common factor across each row and column on the sides.
::在两侧每一行和列上写上最大的共同系数。

The sides of the area model are the factors of the quadratic!
::区域模型的两边是二次方的因素!

Let's try using the method described above to factor $\begin{aligned} x^{2} + 2 x - 15. \end{aligned}$
::让我们尝试使用上文描述的乘数 x2+2x- 15 的方法。

Draw a 2 by 2 area model. Fill in the bottom -left with the quadratic term and the top -right with the constant term. Then draw a large X and write $\begin{aligned} 2 x \end{aligned}$ on the top and $\begin{aligned} - 15 x^{2} \end{aligned}$ on the bottom .
::绘制 2 乘 2 区域模型。填充左下角, 填充四边词, 填充右上角, 填充常数。然后绘制一个大的 X, 在顶部写 2x , 在底部写 ~ 15x2 。

Next, find two terms that add to the top $\begin{aligned} (2 x) \end{aligned}$ and multiply to the bottom $\begin{aligned} (- 15 x^{2}) . \end{aligned}$ The best way to approach this is to list factor pairs for -15 and test their sums.
::下一步,找到两个词,在上方增加2x,在下方增加2x,在下方增加1-15x2。最好的办法就是列出-15的因子对,并测试其数值。

$\begin{aligned} - 1 \cdot 15 = - 15 & and - 1 + 15 = 14 \\ - 15 \cdot 1 = - 15 & and - 15 + 1 = - 14 \\ - 5 \cdot 3 = - 15 & and - 5 + 3 = - 2 \\ - 3 \cdot 5 = - 15 & and - 3 + 5 = 2 \end{aligned}$

::-1+15 15和-1+15=14-15-151 15和-15+1 14-53 15和-5+3+2-3-5 15和-3+5=2

The sides of the X will be $\begin{aligned} - 3 x and 5 x . \end{aligned}$ Fill in the remaining squares of the area model with the two terms we found from the X .
::X的两侧将是-3x和-5x。用我们从X中发现的两个条件填充区域模型的剩余方块。

Lastly, factor out the greatest common factor across each row and column to find the sides of the area model.
::最后,将每个行和列的最大共同因素考虑在内,以找到区域模型的两边。

First row: the greatest common factor between $\begin{aligned} - 3 x and - 15 \end{aligned}$ is $\begin{aligned} - 3. \end{aligned}$
::第一行:-3x和-15之间最大的共同系数是-3。

Second row: the greatest common factor between $\begin{aligned} x^{2} and 5 x \end{aligned}$ is $\begin{aligned} x . \end{aligned}$
::第二行:x2和5x之间最大的共同系数是x。

First column: the greatest common factor between $\begin{aligned} x^{2} and - 3 x \end{aligned}$ is $\begin{aligned} x . \end{aligned}$
::第一列: x2 和 3x 之间最大的共同系数是 x。

Second column: the greatest common factor between $\begin{aligned} 5 x and - 15 \end{aligned}$ is $\begin{aligned} 5. \end{aligned}$
::第二栏:5x至15之间最大的共同系数是5。

The quadratic in factored form is $\begin{aligned} (x - 3) (x + 5) . \end{aligned}$
::系数形式的二次曲线为(x-3)(x+5)。

$\begin{aligned} x^{2} + 2 x - 15 = (x - 3) (x + 5) \end{aligned}$

::x2+2x- 15=(x-3)(x+5)

Example 4-1
::例4-1

Factor $\begin{aligned} 24 x^{2} - 30 x - 9. \end{aligned}$
::24x2-30x-9因数

Solution: Before setting up the area model, we can see that $\begin{aligned} 24 x^{2} - 30 x - 9 \end{aligned}$ has a GCF of 3. Factoring out the 3 will result in $\begin{aligned} 3 (8 x^{2} - 10 x - 3), \end{aligned}$ so we just need to focus on $\begin{aligned} 8 x^{2} - 10 x - 3 \end{aligned}$ when factoring.
::解决方案:在建立区域模型之前,我们可以看到24x2-30x-9全球合作框架为3。将3乘以3将产生3(8x2-10x-3),因此我们只需在计分时注重8x2-10x-3即可。

Start by setting up the area model and the X . The top is the linear term, $\begin{aligned} - 10 x . \end{aligned}$ The bottom is product of the diagonals, $\begin{aligned} (8 x^{2}) (- 3) = - 24 x^{2} . \end{aligned}$

::以设置区域模型和 X 开始。顶部是线性术语 - 10x 。底部是对角的产物 , (8x2)(-3) 24x2 。

We are looking for two terms that multiply to $\begin{aligned} - 24 x^{2} \end{aligned}$ and add to $\begin{aligned} - 10 x . \end{aligned}$ Check the factor pairs of -24 to find a pair that adds to -10.
::我们正在寻找乘以 - 24x2 并加到 - 10x 的两个条件。检查 - 24 的因子对, 找到一个加到 - 10 的因子对。

$\begin{aligned} - 1 + 24 & = 23 \\ - 24 + 1 & = - 23 \\ - 2 + 12 & = 10 \\ - 12 + 2 & = - 10 \end{aligned}$

So the sides of the X are $\begin{aligned} - 12 x \end{aligned}$ and $\begin{aligned} 2 x . \end{aligned}$ Fill in the remaining squares of the area model with the two terms we found from the X .
::X 的两边是 - 12x 和 2x 。填充区域模型的剩余方块, 填充 X 中的两个条件。

Then, find the sides of the area model by factoring out the GCF of each row and column.
::然后通过考虑到每一行和列的绿色气候基金,找出区域模型的两边。

From the sides of the area model, we see that t he quadratic in factored form is $\begin{aligned} 3 (2 x - 3) (4 x + 1) . \end{aligned}$
::从区域模型的两边看,我们可以看到,系数化的二次方形是3(32x-3)(4x+1)。

$\begin{aligned} 24 x^{2} - 30 x - 9 = 3 (8 x^{2} - 10 x - 3) = 3 (2 x - 3) (4 x + 1) \end{aligned}$

::24x2-30x-9=3(8x2-10x-3)=3(2x-3)(4x+1)

Work it Out
::工作出来

Factor each of the following:
::以下每种因素的因数:

$\begin{aligned} \begin{array}{ll} a. & x^{2} + 7 x + 6 \\ b. & x^{2} + 7 x + 12 \\ c. & x^{2} + 8 x + 15 \\ d. & x^{2} + 10 x + 21 \\ e. & x^{2} + 3 x + 2 \\ f. & 25 x^{2} + 30 x + 9 \\ g. & 5 x^{2} + 18 x + 9 \\ h. & 10 x^{2} - x - 3 \\ i. & 3 x^{2} + 2 x - 8 \\ j. & 4 x^{2} + 8 x + 3 \\ k. & 5 x^{2} - 35 x + 60 \end{array} \end{aligned}$
::ax2+7x+6b.x2+7x+6b.x2+7x+6b.x2+7x+12c.x2+8x+15d.x2+10x+21e.x2+3x+2f.25x2+30x+9g.5x2+18x+9g.5x2+18x+9h.10x2-x-3i3x2+2x8j.4x2+8x+3k5x2+35x60

Summary
::摘要

The area of a rectangle can be written as a product of its overall dimensions, or as the sum of the area of individual regions.
::矩形区域可以写成是其整体维度的产物,也可以写成个别区域区域面积的总和。

A quadratic expression can be written as the product of two factors, or as the sum of a quadratic, linear, and constant term.
::二次表达式可以是两个因素的产物,也可以是二次、直线和恒定术语的总和。

You can use an area model to convert quadratic expressions between factored and expanded form.
::您可以使用一个区域模型来转换因子窗体和扩展窗体之间的二次表达式。

PLIX Interactive
::PLIX 交互式互动

分配和保理

Section outline

The Purpose of this Lesson
::本课程的目的

Activity 1 : Distribution by Calculating the Area of a Square

::活动1:通过计算广场面积进行分配

Example 1-1
::例1-1

Work it Out
::工作出来

Interactive
::交互式互动

Factored Form vs. Expanded Form for a Polynomial
::乘数表对多面体扩大表

Interactive
::交互式互动

Activity 2: Distribute by Calculating Area of a Rectangle
::活动2:通过矩形的计算区域进行分布

Interactive
::交互式互动

Activity 3: Factoring Given Area of Regions
::活动3:按特定区域确定区域因素

Example 3-1
::例3-1

Work it Out
::工作出来

Interactive
::交互式互动

Activity 4: Factoring Quadratic Expressions
::活动4:计算二次曲线表达式

Factor Using Area Models
::使用面积模型的因数

Using the Area Model to Factor a Quadratic Expression
::使用“区域模型”来乘以二次曲线表达式

Example 4-1
::例4-1

Work it Out
::工作出来

Summary
::摘要

PLIX Interactive
::PLIX 交互式互动

Section outline

The Purpose of this Lesson ::本课程的目的

Activity 1 : Distribution by Calculating the Area of a Square ::活动1:通过计算广场面积进行分配

Example 1-1 ::例1-1

Work it Out ::工作出来

Interactive ::交互式互动

Factored Form vs. Expanded Form for a Polynomial ::乘数表对多面体扩大表

Interactive ::交互式互动

Activity 2: Distribute by Calculating Area of a Rectangle ::活动2:通过矩形的计算区域进行分布

Interactive ::交互式互动

Activity 3: Factoring Given Area of Regions ::活动3:按特定区域确定区域因素

Example 3-1 ::例3-1

Work it Out ::工作出来

Interactive ::交互式互动

Activity 4: Factoring Quadratic Expressions ::活动4:计算二次曲线表达式

Factor Using Area Models ::使用面积模型的因数

Using the Area Model to Factor a Quadratic Expression ::使用“区域模型”来乘以二次曲线表达式

Example 4-1 ::例4-1

Work it Out ::工作出来

Summary ::摘要

PLIX Interactive ::PLIX 交互式互动

The Purpose of this Lesson
::本课程的目的

Activity 1 : Distribution by Calculating the Area of a Square

::活动1:通过计算广场面积进行分配

Example 1-1
::例1-1

Work it Out
::工作出来

Interactive
::交互式互动

Factored Form vs. Expanded Form for a Polynomial
::乘数表对多面体扩大表

Interactive
::交互式互动

Activity 2: Distribute by Calculating Area of a Rectangle
::活动2:通过矩形的计算区域进行分布

Interactive
::交互式互动

Activity 3: Factoring Given Area of Regions
::活动3:按特定区域确定区域因素

Example 3-1
::例3-1

Work it Out
::工作出来

Interactive
::交互式互动

Activity 4: Factoring Quadratic Expressions
::活动4:计算二次曲线表达式

Factor Using Area Models
::使用面积模型的因数

Using the Area Model to Factor a Quadratic Expression
::使用“区域模型”来乘以二次曲线表达式

Example 4-1
::例4-1

Work it Out
::工作出来

Summary
::摘要

PLIX Interactive
::PLIX 交互式互动