Section: 线性平方系统 | 4.3 线性赤道系统-interactive

Section outline

The Purpose of This Lesson
::本课程的目的

In this lesson, you will create and explore systems of equations. You'll learn methods for finding the solutions to such systems, and interpret the meaning of such solutions.
::在这个教训中,你将创造和探索方程体系。你会学习如何找到这些体系的解决方案,并解释这些解决方案的含义。

Introduction : The Graph of an Equation is the Solution Set
::导言:方形图是解决方案集

Work it Out
::工作出来

A base jumper jumps from a tall cliff

A base jumper jumps from a 1.3 kilometer tall cliff. She glides along a straight path towards the flat ground at the base of the cliff , then pulls her parachute and glides along the same linear path to the the ground. She drops 3 meters for every 7 meters of horizontal movement. Create an equation and graph to model the scenario. Find and give the coordinates of her landing point. Graph the line $\begin{aligned} x = 500. \end{aligned}$ Determine her height when she has travelled a half kilometer horizontally . Does she pass through the point (700, 900)? How do you know?
::从1.3公里高的悬崖上跳下基底跳跃。她沿着直径滑行向悬崖底的平地滑行, 然后拉起降落伞和滑行向地面的同一线性路径。她每水平移动7米就跌下3米。创建一个方程式和图形来模拟情景。查找并给出着陆点的坐标。绘制行距 x= 500 。当她水平行走半公里时, 确定她的高度。她是否通过点( 700, 900 ) ? 你怎么知道 ?

Given the line $\begin{aligned} 2 x - 5 y = 7, \end{aligned}$ find the $\begin{aligned} x \end{aligned}$ and $\begin{aligned} y \end{aligned}$ - intercepts , and find one additional point on the line. What is the domain and range for the line? Find the . Is the point (5,1) on the line? How do you know?
::根据 2x- 5y= 7 行, 找到 x 和 y 界面, 在线上另找到一个点。该线的域和范围是什么 ? 查找。点 (5, 1) 在线上吗 ? 你怎么知道 ?

Graph the line $\begin{aligned} x = - 2. \end{aligned}$ Give several points on the line, and several points not on the line. What distinguishes them? What is the domain and range for this line? Is this a function ? How do you know?
::绘制行 x%% 2 。给线上几个点, 并给一些点而不是线上。是什么区别? 此行的域和范围是什么? 这是函数吗 ? 你怎么知道 ?

A robot lawn mower is on a tether tied to the center of a lawn . The tether is 10 meters long. Create an equation which models the path of maximum distance from the tether point (the origin) that the mower can travel. Give the coordinates of 5 points that are on the path. Is the point (7,7) on the graph? How do you know? Graph the line $\begin{aligned} y = 7. \end{aligned}$ Find the intersection points of this line with the graph of the path.
::机械人割草机的绳索被绑在草坪中心。绳索长度为 10 米。创建一个公式, 用来模拟离割草机可以穿行的绳索点( 原点) 的最大距离路径。给出路径上 5 个点的坐标。点( 7 7) 是否在图上 ? 您怎么知道 ? 绘制线条 y = 7 。找到这条线与路径图的交叉点。

Activity 1: Solving a Linear System with the Transitive Property
::活动1:解决带有过境财产的线性系统

So far you've already solved linear systems using the method described below, but now you will generalize the technique.
::到目前为止,你已经用下面描述的方法解决了线性系统, 但现在你将推广这个技术。

Example 1-1
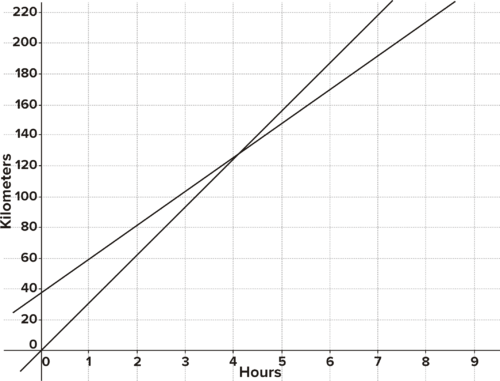
::例1-1

Ayesha is a cyclist is riding at 31 kilometers per hour. Paul is riding at 22 kilometers per hour, but gets a head start of 37 kilometers. Write equations to model the distance each cyclist has travelled as a function of time. Graph. Write and solve an equation to determine when Ayesha passes Paul. Give the distance each has traveled at this time. Explain each step in the solution and confirm the solution in terms of the graphs.
::Ayesha 是一个骑自行车的骑手, 时速为31公里。 Paul 时速为22公里, 但头起点为37公里。写方程式来模拟每个骑自行车的行进距离。图表。写入和解析一个方程式以确定 Ayesha 何时通过 Paul 。给每个行进的距离。解释解决方案中的每一个步骤, 并以图表的形式确认解决方案。

Solution: The equations for each are below. This is called a system of equations. Each equation has a different solution set .
::解答: 每种方程式的方程式如下。这称为方程式系统。每个方程式都有不同的方程式设置。

$\begin{aligned} \begin{array}{l} y = 31 x \\ y = 22 x + 37 \end{array} \end{aligned}$

::y=31xy=22x+37

This is clear from the graphs:
::从图表中可以清楚地看出这一点:

Ayesha and Paul are cyclists. Ayesha rides faster, but Paul has a head start. When does Ayesha pass Paul?
::Ayesha和Paul是骑自行车的。Ayesha骑得更快,但Paul有一个开始。Ayesha什么时候通过Paul?

To determine when Ayesha passes Paul, you write and solve a new equation. You want to find the $\begin{aligned} x \end{aligned}$ -value that returns the same $\begin{aligned} y \end{aligned}$ -value for both functions. This is called solving the system . When solving a system, the meaning of $\begin{aligned} x \end{aligned}$ and $\begin{aligned} y \end{aligned}$ becomes narrower. $\begin{aligned} x \end{aligned}$ and $\begin{aligned} y \end{aligned}$ now signify only the values of those ordered pairs that make both equations true . You seek the specific point(s) $\begin{aligned} (x, y) \end{aligned}$ such that:
::要确定 Ayesha 何时通过 Paul, 您将写入并解析一个新的方程式。您想要找到两个函数返回相同的 Y 值的 x 值。这叫解析系统。当解决一个系统时, x 和 y 的含义将变得狭窄。 x 和 y 现在只表示使两个方程式都真实的定购对子的值。您想要找到具体点( x y) , 具体点如下:

$\begin{aligned} \begin{array}{l} y = 31 x \\ and \\ y = 22 x + 37 \end{array} \end{aligned}$

::y=31xandy=22x+37

By the transitive property of equality*, you can write:
::以平等的过渡性财产* ,您可以写:

$\begin{aligned} 31 x = 22 x + 37 \end{aligned}$

::31x=22x+37

Now solve for $\begin{aligned} x : \end{aligned}$
::现在解析 x:

$\begin{aligned} \begin{array}{ll} 31 x = 22 x + 37 & Transitive property of equality \\ 9 x = 37 & Subtraction property of equality \\ x = \frac{37}{9} = 4 \frac{1}{9} hours & Division property of equality \end{array} \end{aligned}$

::31x=22x+37等值的过渡性财产9x=37等值财产3x=379=419小时

This is the $\begin{aligned} x \end{aligned}$ -coordinate of the ordered pair that makes both equations true. Substituting this value into either equation returns the corresponding $\begin{aligned} y \end{aligned}$ -value. The resulting ordered pair is the solution to the system:
::这是定购对配的 x 坐标, 使两个方程式都真实。将此值转换成任意一个方程式, 返回相应的 Y 值。由此产生的定购对是系统的解决办法 :

$\begin{aligned} \begin{array}{ll} Substituting in First Equation & Substituting in Second Equation \\ y = 31 (\frac{37}{9}) & y = 22 (\frac{37}{9}) + 37 \\ y = \frac{1147}{9} & y = \frac{814}{9} + \frac{333}{9} \\ y = 127 \frac{4}{9} kilometers & y = 127 \frac{4}{9} kilometers \end{array} \end{aligned}$

::以第二等号中第二级等号替代第一个等号=31(379)y=22(379)+37y=11479y=8149+3339y=12749公里=12749公里=12749公里

Substituting $\begin{aligned} x = 4 \frac{1}{9} \end{aligned}$ into the second equation confirms the result--it is not necessary except to check your work. Your work can also be confirmed with the graph. The intersection of the two lines is the point:
::在第二个方程中将 x=419 替换为 x= 419 确认结果 - 除了检查您的工作以外, 不需要结果 - 不需要结果 - 只需检查您的工作。您的工作也可以与图形确认。两行的交叉点是 :

$\begin{aligned} (4 \frac{1}{9}, 127 \frac{4}{9}) \end{aligned}$

*The transitive property of equality: If $\begin{aligned} a = b \end{aligned}$ and $\begin{aligned} b = c, \end{aligned}$ then $\begin{aligned} a = c . \end{aligned}$
::* 平等的过渡财产:如果a=b和b=c,那么a=c。

Solving a Linear System with the Transitive Property
::解决带有过境财产的线性系统

Given a system of linear equations of the form:
::考虑到表单的线性方程系统:

$\begin{aligned} \begin{array}{l} y = a x + b \\ y = c x + d \end{array} \end{aligned}$
This system can be solved by writing and solving the equation:
$\begin{aligned} a x + b = c x + d \end{aligned}$

::y=ax+b=cx+d 此系统可以通过写入和解析方程式: exax+b=cx+d来解析

Work it Out
::工作出来

Ayesha and Paul ride on another day. Paul rides at 28 kilometers per hour. Ayesha rides at 19 kilometers per hour, but starts 2 hours later. Write equations to model the distance each cyclist has travelled as a function of time. Graph. Write and solve an equation to determine when Paul passes Ayesha . Give the distance each has traveled at this time. Explain your solution in terms of the graphs.
::Ayesha 和 Paul 在另一天骑马。 Paul 骑车时速为28公里。 Ayesha 骑车时速为19公里,但从2小时后开始。写方程式来模拟每个骑自行车的行驶距离。图表。写入和解析一个方程式以确定 Paul 何时通过 Ayesha 。给每个骑车时速为28公里。请用图表解释您的解决方案。

In order to use the transitive property to solve a linear system, each equation must be in slope-intercept form . Convert each of the following to slope-intercept form. An example is provided.
::为了使用中转属性解决线性系统,每个方程式必须以斜坡界面的形式。以下方程式转换为斜坡界面。例举一例。

$\begin{aligned} \begin{array}{ll} a. & - 2 y = 5 x \\ b. & 4 y + 2 = 8 x \\ c. & 3 x - 5 y = 9 \\ d. & π x + e y = 0 \\ e. & a x + b y = c \\ f. & \frac{x}{a} + \frac{y}{b} = 1 \end{array} \end{aligned}$
::a.-2y=5xb.4y+2=8xc.3x-5y=9d.x+ey=0e.ax+by=cf.xa+yb=1

$\begin{aligned} \begin{array}{ll} Equation & Explanation \\ 7 x - \frac{2}{3} y = 5 & Given equation. \\ - \frac{2}{3} y = - 7 x + 5 & Subtraction property of equality. \\ - \frac{3}{2} \cdot (- \frac{2}{3} y) = - \frac{3}{2} (- 7 x + 5) & Multiplication property of equality. \\ y = - \frac{3}{2} (- 7 x + 5) & Simplification of left side. \\ y = \frac{21}{2} x - \frac{15}{2} & Distribution. \end{array} \end{aligned}$

::EquationExplantation7x-23y=5 Felenten 等式。 - 23y7x+5 平等减量属性。 - 32(- 23y)32(- 7x+5) 平等乘法属性。 y32(- 7x+5) (- 7x+5) 简化左侧。y= 212x-152 分配。

Use the transitive property of equality to solve the system:
::利用平等的过渡性财产解决系统问题:

$\begin{aligned} \begin{matrix} y + 10 = 4 x \\ 3 y - x = 12 \end{matrix} \end{aligned}$

::y+10=4x3y-x=12 y+10=4x3y-x=12

Activity 2: Solving Linear Systems with Substitution
::活动2:用替代办法解决线性系统的解决

In the course , you've used substitution frequently. For example, if $\begin{aligned} y = 2 x + 3 and x = 4, \end{aligned}$ then:
$\begin{aligned} \begin{array}{l} y = 2 (4) + 3 \\ y = 11 \end{array} \end{aligned}$

::在课程中, 您经常使用替换。例如, 如果y= 2x+3 和 x= 4, 那么:y= 2(4)+3y=11

Typically this sort of substitution is thought of as the process for determining the $\begin{aligned} y \end{aligned}$ -value returned for a particular $\begin{aligned} x \end{aligned}$ -value. But it can also be thought of as solving a system of equations , the second of which is the equation $\begin{aligned} x = 4 : \end{aligned}$
::通常,这种替代被认为是用来确定一个特定的 x 值返回的 Y 值的过程。但它也可以被认为是用来解决一个方程式系统, 其中第二个是公式 x= 4 :

$\begin{aligned} \begin{array}{l} y = 2 x + 3 \\ and \\ x = 4 \end{array} \end{aligned}$

::y=2x+3和x=4

As was the case with the use of the transitive property previously, solving the system means interpreting $\begin{aligned} x \end{aligned}$ as representing the same value(s) in both equations. As you'll see in the following example, the substitution method can be used to solve any linear system. I t is fine to substitute for either variable .
::正如以前使用过境财产的情况一样,解决系统意味着将x解释为代表两个方程中的相同值。如下表所示,替代方法可用于解决任何线性系统。替换任何一个变量都是可以的。

Example 2-1
::例2-1

Two couples are taking two cars on a road trip from San Diego to the end of the Baja peninsula, 900 miles away. The first couple is Xander and Yana , and they always drive at 45 and 90 miles per hour respectively. The second couple is Xena and Ynes, and they always drive at 80 and 4 0 miles per hour respectively. Create equations which model the relationship between the hours each person drives. Xander and Xena want to drive the same number of hours, and Yana and Ynes want to drive the same number of hours. Solve the system to determine the number of hours they must drive to accomplish this goal.
::两对夫妇在从圣地亚哥到巴哈半岛终点的公路旅行中乘坐两辆汽车,距离900英里。第一对夫妇是Xander和Yana, 车速总是每小时45英里和90英里。第二对夫妇是Xena和Ynes,车速总是每小时80英里和40英里。创建方程式,以模拟每个人驾驶的时数之间的关系。Xander和Xena想要驾驶的时数相同,Yana和Ynes想要驾驶的时数相同。关闭这个系统以决定他们为实现这一目标必须驾驶的时数。

Solution: The variable $\begin{aligned} x \end{aligned}$ represents the number of hours driven by Xander and Xena. The variable $\begin{aligned} y \end{aligned}$ represents the number of hours driven by Yana and Ynes.
::解答:变量x代表Xander和Xena驾驶的小时数。变量y代表Yana和Ynes驾驶的小时数。

Here is the system:
::以下是这个系统:

$\begin{aligned} \begin{array}{l} 45 x + 90 y = 900 \\ 80 x + 40 y = 900 \end{array} \end{aligned}$

::45x+90y=90080x+40y=900

Converting the second one to slope-intercept form:
::将第二个转换为斜坡界面:

$\begin{aligned} \begin{array}{l} 80 x + 40 y = 900 \\ 40 y = - 80 x + 900 \\ y = - 2 x + 22.5 \end{array} \end{aligned}$

::80+40y=9004ny80x+900y2x+22.5

If $\begin{aligned} 45 x + 90 y = 900 and y = - 2 x + 22.5, \end{aligned}$ then by substitution:
::如果45x+90y=900和y2x+22.5,则代之以:

$\begin{aligned} \begin{array}{l} 45 x + 90 (- 2 x + 22.5) = 900 \\ 45 x - 180 x + 2025 = 900 \\ - 135 x + 2025 = 900 \\ - 135 x = - 1125 \\ x = 8 \frac{1}{3} \\ y = - 2 (8 \frac{1}{3}) + 22.5 \\ y = - 16 \frac{2}{3} + \frac{45}{2} \\ y = - \frac{100}{6} + \frac{135}{6} \\ y = 5 \frac{5}{6} \\ (8 \frac{1}{3}, 5 \frac{5}{6}) \end{array} \end{aligned}$

::45x90(- 2x+22.5)=90045x-180x+2025=9000-135x+2025=9000-135x+2025=9000-135x1125x=813y2(813)+22.5y1623+452y1006+1356y=556(813556)

If each couple divides their driving as shown, then both Xander and Xena will drive $\begin{aligned} 8 \frac{1}{3} \end{aligned}$ hours, and Yana and Ynes will drive $\begin{aligned} 5 \frac{5}{6} \end{aligned}$ hours. Both couples will arrive at their destination at the same time.
::如果每对夫妇的驾驶都按所示分开,那么Xander和Xena将驾驶813小时,Yana和Ynes将驾驶556小时,这两对夫妇将同时到达目的地。

Two couples take two cars on a road trip from San Diego

Solving Linear Systems with Substitution
::具有替代作用的解决线性系统

Given a linear system such that only one is solved for one variable, as in:
::鉴于一个线性系统,只有一个变数解答了一个变数,例如:

$\begin{aligned} \begin{array}{l} a x + b y = c \\ y = d x + g \end{array} \end{aligned}$

::ax+by=cy=dx+g (ax+by=cy=dx+g)

This system can be solved by substituting the expression for $\begin{aligned} y \end{aligned}$ in the second equation in place of $\begin{aligned} y \end{aligned}$ in the first equation:
::要解决这个系统,可以用第二个方程式中的y表示法取代第一个方程式中的y表示法:

$\begin{aligned} a x + b (d x + g) = c \end{aligned}$

::ax+b(dx+g)=c

It's fine to substitute for $\begin{aligned} x \end{aligned}$ as well.
::代替x也没关系

Work it Out
::工作出来

It takes one factory 5 days to process a ton of corn, and 2 days to process a ton of soybeans. The factory can run for 20 days before it's shut down for maintenance. Another factory takes 3 days per ton of corn and 6 days per ton of soybeans, and the factory can run 30 days before it's shut for maintenance. Write equations which relate the tons of corn and soybeans each factory can produce. Graph the functions. The owner of both factories wants each to produce the same amount of corn, and the same amount of soybeans. Find these quantities.
::处理一吨玉米需要5天,加工一吨大豆需要2天。工厂在关闭维修前可以运行20天。另一家工厂每吨玉米需要3天,大豆需要6天,工厂需要30天才能关闭维修。写出每个工厂能够生产的玉米和大豆的方程式。绘制功能图。两家工厂的业主都想生产同样数量的玉米和大豆。找出这些数量。

Solve the system:
$\begin{aligned} \begin{array}{l} y = 3 x - 5 \\ 2 x + 3 y = 4 \end{array} \end{aligned}$

::解决系统: y=3x- 52x+3y=4

Solve the system:
$\begin{aligned} \begin{array}{l} x = 3 y - 5 \\ 2 x + 3 y = 4 \end{array} \end{aligned}$

::解决系统:x=3y-52x+3y=4

Create two equations for lines with the same slope but different $\begin{aligned} y \end{aligned}$ -intercepts. Graph the functions. Does this system have a solution? Why or why not? Use the techniques explored in this section to attempt to solve the system. Interpret and generalize your results.
::为具有相同斜度但有不同 y 界面的线条创建两个方程式。绘制函数。绘制函数。这个系统是否有解决办法? 为什么或为什么没有? 使用本节所探讨的技术来尝试解析系统。解释和概括您的结果。

The following lines form an unusual system of equations. Convert each to slope-intercept form. What do you observe? In how many points do these two lines intersect? Solve the system using techniques explored in this section. Interpret and generalize your results.
::以下的线条形成一个不寻常的方程系统。将每个线条转换为斜坡界面。您观察什么? 这两条线交错了多少点? 使用本节所探讨的技术解决了这个系统。解释并概括了您的结果。

$\begin{aligned} \begin{array}{l} 5 x - 7 y = 11 \\ 15 x - 21 y = 33 \end{array} \end{aligned}$

::5x-7y=1115x-21y=33

Activity 3: Solving Linear Systems by Elimination
::活动3:通过消除解决线性系统

When linear equations in a system are in standard form , the elimination method is an option for solving the system. Here's how it works:
::当系统中的线性方程式以标准形式出现时,消除法是解决系统的一个选项。

Suppose:
$\begin{aligned} \begin{array}{l} a = b \\ and \\ c = d \end{array} \end{aligned}$

::假设:a=bandc=d

The addition property of equality means you can add $\begin{aligned} c \end{aligned}$ to both sides of the first equation:
::添加平等财产意味着您可以在第一个等式的两侧添加 c:

$\begin{aligned} \begin{array}{l} a = b \\ + c + c \\ a + c = b + c \end{array} \end{aligned}$

::a = b+c+ca+c=b+c

Because $\begin{aligned} c = d, \end{aligned}$ $\begin{aligned} d \end{aligned}$ can be substituted for $\begin{aligned} c : \end{aligned}$
::因为c=d, d 可替代 c:

$\begin{aligned} \begin{array}{l} a = b \\ + c + d \\ a + c = b + d \end{array} \end{aligned}$

::a = b+c +da+c=b+d = b+c +da+c=b+d

In general, this means that when solving a system, you can add the two equations:
::一般来说,这意味着当解决一个系统时,你可以加上两个方程式:

$\begin{aligned} \begin{array}{l} a = b \\ c = d \\ a + c = b + d \end{array} \end{aligned}$

::a = b c = da+c= b+d

This method can be used to eliminate variables, as shown in the subsequent examples. It is fine to eliminate either variable, or to subtract instead of add to eliminate variables.
::如随后的例子所示,这一方法可用于消除变量。删除变量或减去变量,而不是添加来消除变量,是罚款的。

Example 3-1
::例3-1

Solve the system using the elimination method. Note that in this case, $\begin{aligned} - 2 y \end{aligned}$ and $\begin{aligned} 2 y \end{aligned}$ will be eliminated by addition :
::使用消除方法解决系统。注意在此情况下, 2- 2y 和 2y 将通过以下方式予以消除:

$\begin{aligned} \begin{array}{l} 5 x - 2 y = 10 \\ x + 2 y = 4 \end{array} \end{aligned}$

::5x-2y=10x+2y=4

Solution:
::解决方案 :

$\begin{aligned} \begin{array}{l} 5 x - 2 y = 10 \\ x + 2 y = 4 \\ 6 x = 14 \\ x = 2 \frac{1}{3} \\ 2 \frac{1}{3} + 2 y = 4 \\ 2 y = 1 \frac{2}{3} \\ y = \frac{5}{6} \\ (2 \frac{1}{3}, \frac{5}{6}) \end{array} \end{aligned}$

::5x-2y=10x+2y=4 6x=14x=213213+2y=42y=123y=223y=56(213,56)

Example 3-2
::例3-2

In some cases, you won't have equations such that one variable is immediately eliminated by addition or subtraction . But the multiplication property of equality gives us a way to solve that obstacle. The system below does not feature any variables whose coefficients have the same magnitude. In the solution, observe how to multiply both sides of each equation such that the coefficient of $\begin{aligned} y \end{aligned}$ in both equations is the least common multiple of the original coefficients. Then observe that you subtract to eliminate.
::在某些情况下, 您不会拥有这样的等式, 以至于一个变数会立即被增减来消除。但平等的倍增属性给了我们解决这个障碍的方法。下面的系统并不包含任何系数大小相同的变数。在解决方案中, 观察如何将每个等式的两边乘以, 使 y 系数在两个等式中是原始系数中最不常见的倍数。然后观察您减去以去掉。

$\begin{aligned} \begin{array}{l} 3 x + 2 y = 1 \\ 5 x + 5 y = 2 \end{array} \end{aligned}$

::3x+2y=15x+5y=2

Solution:
::解决方案 :

$\begin{aligned} \begin{array}{l} 5 (3 x + 2 y = 1) \\ 2 (5 x + 5 y = 2) \\ 15 x + 10 y = 5 \\ 10 x + 10 y = 4 \\ 5 x = 1 \\ x = \frac{1}{5} \\ 3 (\frac{1}{5}) + 2 y = 1 \\ \frac{3}{5} + 2 y = 1 \\ y = \frac{1}{5} \\ (\frac{1}{5}, \frac{1}{5}) \end{array} \end{aligned}$

::5( 3x+2y=1) 2( 5x+5y=2) 15x+10y=510x+10y=4 5x=1xx=1x=153( 15)+2y=135+2y=1y=15( 15) 15

Solving Systems with Elimination
::消除解决系统

Given a system in standard form:
::根据标准格式的系统:

$\begin{aligned} \begin{array}{l} a x + b y = c \\ d x + f y = g \end{array} \end{aligned}$

::ax+by=cdx+fy=g =xx+by=cdx+fy=g =xx=cdx+fy=g =xx+by=cdx+fy=g

The system can be solved by elimination:
::该系统可以通过消除下列因素来解决:

First, m ultiply one or both equations by factors which make it so that two coefficients of the same variable are equals or equal opposites.
::首先,乘以一个或两个方程的系数,使两个变量的系数相等或对等。

Then, add or subtract to eliminate either $\begin{aligned} x \end{aligned}$ or $\begin{aligned} y . \end{aligned}$
::然后加上或减去以删除 x 或 y。

Work it Out
::工作出来

Solve the system :
$\begin{aligned} \begin{array}{l} x + 2 y = 1 \\ 3 x + 4 y = 2 \end{array} \end{aligned}$

::解决系统: x+2y=13x+4y=2

Solve the system :
$\begin{aligned} \begin{array}{l} 4 x - 5 y = 3 \\ 7 x + 2 y = 1 \end{array} \end{aligned}$

::解决系统: 4x-5y=37x+2y=1

Solve the system from Example 2-1 using the elimination method:
$\begin{aligned} \begin{array}{l} 45 x + 90 y = 900 \\ 80 x + 40 y = 900 \end{array} \end{aligned}$

::使用消除方法从例2-1中解决系统: 45x+90y=90080x+40y=900

Solve the system below using elimination, then independently solve it using the transitive property of equality:
::解决以下制度,利用消除,然后利用平等的过渡性财产独立解决:

$\begin{aligned} \begin{array}{l} x = 2 y + 3 \\ x = 3 y - 4 \end{array} \end{aligned}$

::x=2y+3x=3y-4

Create a system of linear equations that has the point (0,9) as its only solution.
::创建一个以点( 0,9) 为其唯一解决方案的线性方程式系统。

Create a system of linear equations that has the point (0,0) as its only solution.
::创建一个以点( 0,0)为唯一解决方案的线性方程式系统。

Create a system of linear equations that has an infinite number of solutions.
::创建一个线性方程式系统, 该系统有无限数的解决方案。

Create a system of linear equations that has no solutions.
::创建一个没有解决方案的线性方程式系统。

Create a system of linear equations that has the point (2,5) as a solution. (Hint: Start with graphing)
::创建一个线性方程式系统, 以点(2, 5)作为解决方案。 (提示: 以图形形式开始)

Interactive
::交互式互动

Use the interactive below to adjust the slope and y − intercept of each equation. Explore various systems of linear equations that give you one solution, no solutions, and an infinite number of solutions.
::使用下面的交互效果来调整每个方程式的斜度和 Y- interview 。探索各种线性方程式系统, 给您一个解决方案, 没有解决方案, 以及无限数量的解决方案。

INTERACTIVE

Solving Linear Systems

Move the sliders to adjust the corresponding terms in the equations of these lines.
::移动滑动符以调整这些行的方程式中相应的条件。

The yellow point/line represents the solution(s).
::黄色点/线代表解决方案。

Your device seems to be offline.
Please check your internet connection and try again.

+

Do you want to reset the PLIX?

Yes

No

Summary
::摘要

The solution to a system of equations is the set of points that make both equations true.
::方程体系的解决方案是将两种方程都变为真实的一组点。

It's visible as the point(s) of intersection of the graphs of each equation.
::它作为每个方程式的图形的交叉点可见。

The transitive property, the substitution method, and the elimination method can be used to solve linear systems.
::中转财产、替代方法和消除方法可用于解决线性系统。

A system of linear equations can have one solution, no solutions, or infinite solutions.
::线性方程式系统可以有一个解决方案,没有解决方案,或无限解决方案。

线性平方系统

Section outline

The Purpose of This Lesson
::本课程的目的

Introduction : The Graph of an Equation is the Solution Set
::导言:方形图是解决方案集

Work it Out
::工作出来

Activity 1: Solving a Linear System with the Transitive Property
::活动1:解决带有过境财产的线性系统

Example 1-1
::例1-1

Solving a Linear System with the Transitive Property
::解决带有过境财产的线性系统

Work it Out
::工作出来

Activity 2: Solving Linear Systems with Substitution
::活动2:用替代办法解决线性系统的解决

Example 2-1
::例2-1

Solving Linear Systems with Substitution
::具有替代作用的解决线性系统

Work it Out
::工作出来

Activity 3: Solving Linear Systems by Elimination
::活动3:通过消除解决线性系统

Example 3-1
::例3-1

Example 3-2
::例3-2

Solving Systems with Elimination
::消除解决系统

Work it Out
::工作出来

Interactive
::交互式互动

Summary
::摘要

Section outline

The Purpose of This Lesson ::本课程的目的

Introduction : The Graph of an Equation is the Solution Set ::导言:方形图是解决方案集

Work it Out ::工作出来

Activity 1: Solving a Linear System with the Transitive Property ::活动1:解决带有过境财产的线性系统

Example 1-1 ::例1-1

Solving a Linear System with the Transitive Property ::解决带有过境财产的线性系统

Work it Out ::工作出来

Activity 2: Solving Linear Systems with Substitution ::活动2:用替代办法解决线性系统的解决

Example 2-1 ::例2-1

Solving Linear Systems with Substitution ::具有替代作用的解决线性系统

Work it Out ::工作出来

Activity 3: Solving Linear Systems by Elimination ::活动3:通过消除解决线性系统

Example 3-1 ::例3-1

Example 3-2 ::例3-2

Solving Systems with Elimination ::消除解决系统

Work it Out ::工作出来

Interactive ::交互式互动

Summary ::摘要

The Purpose of This Lesson
::本课程的目的

Introduction : The Graph of an Equation is the Solution Set
::导言:方形图是解决方案集

Work it Out
::工作出来

Activity 1: Solving a Linear System with the Transitive Property
::活动1:解决带有过境财产的线性系统

Example 1-1
::例1-1

Solving a Linear System with the Transitive Property
::解决带有过境财产的线性系统

Work it Out
::工作出来

Activity 2: Solving Linear Systems with Substitution
::活动2:用替代办法解决线性系统的解决

Example 2-1
::例2-1

Solving Linear Systems with Substitution
::具有替代作用的解决线性系统

Work it Out
::工作出来

Activity 3: Solving Linear Systems by Elimination
::活动3:通过消除解决线性系统

Example 3-1
::例3-1

Example 3-2
::例3-2

Solving Systems with Elimination
::消除解决系统

Work it Out
::工作出来

Interactive
::交互式互动

Summary
::摘要