节: 立方函数和等式 | 4.12 立方函数和等量-interactive | The Way To Learn

The Way To Learn

首页日程管理

章节大纲

The Purpose of this Lesson
::本课程的目的

In this lesson, you will model scenarios with cubic functions. You'll explore the structure of cubic functions and contrast them with quadratic functions.
::在此课中, 您将用立方函数来模拟假设情景。您将探索立方函数的结构, 并将其与二次函数相对照。

Activity 1: The Volume Model
::活动1:数量模型

Interactive
::交互式互动

Tyrone wants to make a box from a rectangular piece of cardboard with dimensions 4 meters by 3 meters. He'll cut squares from each corner and fold up the sides to make the box with an open top. He wants to make the box so it has the maximum volume possible given the constraints.
::Tyrone想用一个4米乘3米宽的长方形纸板做一个盒子。他会把每个角落的方形切开,然后折叠两边, 使盒子上盖开。他想把盒子做成一个开阔的。他想要把盒子做成一个最大容量的盒子, 以适应这些限制。

Use the following interactive to explore the dimensions of the box and the corresponding volume. A pproximate the dimensions of the box that has the maximum volume and the maximum volume. What is the approximate side length of the squares removed from each corner?
::使用以下交互方式来探索框的尺寸和相应的体积。接近有最大体积和最大体积的框的尺寸。从每个角落移除的方形的大约侧长是多少?

INTERACTIVE

Cardboard Box

Move the red slider to change the dimensions of the box cutout.
::移动红色滑动器以改变框切除的尺寸。

Your device seems to be offline.
Please check your internet connection and try again.

+

Do you want to reset the PLIX?

Yes

No

Example 1-1
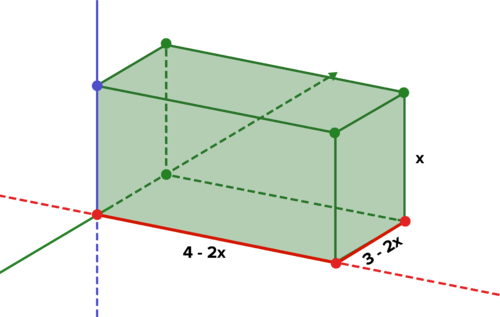
::例1-1

Recall that Tyrone wants to make a box from a rectangular piece of cardboard with dimensions 4 meters by 3 meters by cutting squares from each corner and folding up the sides to make the box with an open top. He wants to make the box so it has the maximum volume possible given the constraints.
::蒂龙想用一个四米三米宽的长方形纸板做一个盒子, 将每个角落的方形切开, 并折叠两边, 使盒子上方开着。他想把盒子做成一个开着的盒子, 从而在限制下, 使盒子的体积达到最大。

Draw a diagram of the original rectangle, and assign a length of $\begin{aligned} x \end{aligned}$ to the sides of the squares. Determine expressions for the dimensions of the box in terms of $\begin{aligned} x . \end{aligned}$ Write an equation for the volume of the box as a function of the side length of the square removed. What is the practical domain for this scenario? Use graphing technology to determine the side length that returns the maximum volume.
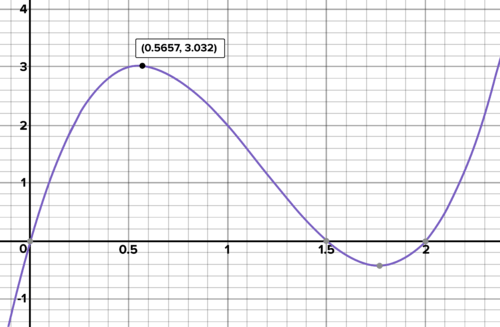
::绘制原始矩形的图表, 并指定方形两侧的 x 长度。确定框内以 x 表示的尺寸的表达式。将方程式的体积写成方程式, 作为被删除方形的侧长度的函数。此方案的实际域是什么? 使用图形化技术来确定返回最大体积的侧长度。

Solution:  The equation for the volume as a function of the side length of the square removed is shown below. Also shown is a diagram of the rectangle, with the dimensions of the resulting rectangular prism shown. See also, a diagram showing the assembled box, with the dimensions labeled. Finally, there is a graph of the function, showing that at a side length of about 0.57 meters, the maximum volume of about 3 cubic meters is achieved. The practical domain for this scenario is [0, 1.5], as the squares cut out cannot be more than half the length of the shortest side of 3 meters.
::解析度: 将音量的方程式作为平方的侧长函数显示如下。也显示矩形图, 并显示由此形成的矩形棱柱的维度。另请参见显示组装框的图表, 并标注尺寸。最后, 有一个函数图, 显示在大约 0. 57 公尺的侧长上, 最大体积为 3 立方公尺。此假设情景的实际域为 [ 0. 15] , 因为平方的切除不能超过 3 公尺最短的侧的长度的一半。

$\begin{aligned} V (x) = (4 - 2 x) (3 - 2 x) x \end{aligned}$

::V(x)=(4-2x)(3-2x)x

Tyrone wants to make a box from a rectangular piece of cardboard with dimensions 4 meters by 3 meters.

A three-dimensional view of the folded box, with sides labeled.

A graph of possible configurations of Tyrone's box

Work it Out
::工作出来

You want to make an open-topped box from a rectangular piece of cardboard measuring 5 meters by 7 meters. Write a function for the volume of the box as a function of the side length of the squares removed. Use graphing technology to approximate the side length that returns the maximum volume.
::您想要从一个5米乘7米的矩形纸板块上做一个打开的框。写入一个函数, 将框的体积作为被删除方形侧长的函数。使用图形化技术来接近返回最大体积的侧长度。

Activity 2: Cubic Functions
::活动2:立体函数

The functions in the previous problems were cubic .
::先前问题中的函数为立方体。

Example 2-1
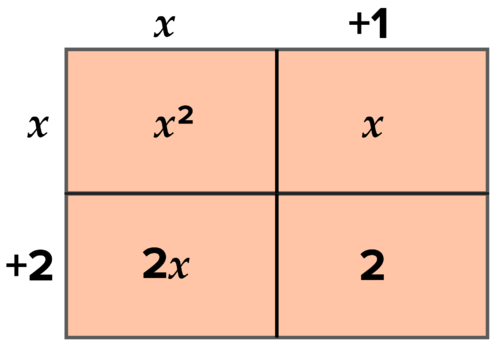
::例2-1

Examples of polynomial functions in both standard and factored form are given below. Discuss and summarize differences and similarities.
::下文举例说明了标准形式和因素形式的多功能,讨论并总结了差异和相似之处。

$\begin{aligned} \begin{array}{clll} Form & Linear & Quadratic & Cubic \\ Standard & y = 2 x + 6 & y = x^{2} - 2 x + 6 & y = 4 x^{3} + x^{2} - 2 x + 6 \\ Standard & y = 4 x & y = 5 x^{2} + x & y = - 7 x^{3} + 2 x^{2} - 3 x \\ Standard & y = - \frac{1}{2} x & y = x^{2} + 5 & y = 2 x^{3} - 9 \\ Factored & y = (x - 2) (x + 4) & y = (x - 3) (x - 1) (x - 9) \\ Factored & y = 5 x (3 x + 4) & y = 3 x (x + 2) (3 x - 5) \\ Factored & y = 3 (x - 6) (2 x + 7) & y = 2 x^{2} (3 x + 10) \\ Factored & y = 5 (x - 4)^{2} & y = 6 (x + 2)^{3} \end{array} \end{aligned}$

::窗体半径立方体= 2x+6y=x2-2x+6y=4x3+x2-2xx6Stardy=4xy=5x2+xy=5x2+x}7x3+2x2x2 -3xStandardy=2x2+5y=2x2+5y=2x3-9Factoredy=(x-2(x+4)y=(x-3(x-1)(x9)Factoredy=5x(3x+4)y=3x(x+2)(3x-5)Factoredy=3(x6)(2x+7)y=2x2(3x)x+10Factoredy=5(x-4)2y=6(x+2)3

Solution:    A linear function consists of a single monomial or binomial . A quadratic can be up to a trinomial , and a cubic can have up to 4 terms. A linear function consists of only one factor , and there is only one possible zero.
::解析: 线性函数由单一单项函数或二元函数组成。二次函数最多可达到三元函数, 立方体最多可达到四个条件。线性函数只包含一个系数, 可能只有一个零。

A quadratic can consist of two factors. Sometimes each factor is the same, meaning the quadratic features a perfect square , as in the last example.
::二次曲线可以由两个因素组成,有时每个因素是相同的,这意味着二次曲线具有完美的方形,如最后一个例子。

A cubic can consist of 1, 2, or 3 factors. Some of those factors can be perfect squares as in the second-to-last example. It's even possible to have a perfect cube as in the last example. In this case, all three factors of the cubic are the same, namely $\begin{aligned} x + 2. \end{aligned}$
::立方体可以由 1, 2 或 3 个因素组成。其中一些因素可以是完美的正方形, 如倒数第二到倒数第二的例子。甚至有可能有一个完美的立方体, 如倒数最后一个例子。在这种情况下, 立方体的所有三个因素都是相同的, 即 x+2 。

Cubic Functions
::立三次函数

A cubic function has a degree of 3, that is, its largest exponent is 3.
::立方函数的度为3,即其最大的指数为3。

It has at most 3 factors, and at most 3 zeroes .
::它最多有三个因素,最多三个零。

Because finding volume involves 3 dimensions multiplied (or similar variations), formulas for volume can be used to create cubic functions.
::由于查找体积涉及3维乘以(或类似的变异),可使用体积公式创建立方函数。

Example 2-2
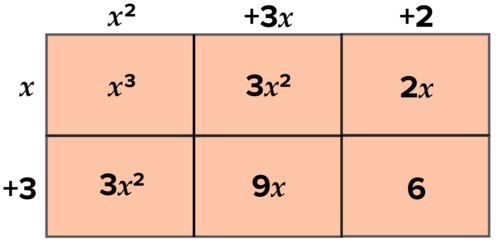
::例2-2

You can use the area method twice to convert a cubic from factored to standard form . Convert the following cubic from factored to standard form. First convert two factors to a quadratic, then draw another diagram that enables you to multiply the remaining factor times the resulting quadratic.
::您可以使用区域方法两次将一个立方体从系数转换为标准窗体。将以下立方体从系数转换为标准窗体。首先将两个因数转换为二次,然后绘制另一个图表,使剩余因数乘以由此产生的二次方体。

$\begin{aligned} y = (x + 3) (x + 1) (x + 2) \end{aligned}$

::y= (x+3)(x+1)(x+2)

Solution:    First, $\begin{aligned} (x + 1) (x + 2) = x^{2} + 3 x + 2 \end{aligned}$ as shown below:
::解决办法:第一,(x+1)(x+2)=x2+3x+2,如下所示:

Multiply (x + 1) by (x + 2)

Now, $\begin{aligned} (x + 3) (x^{2} + 3 x + 2) = x^{3} + 6 x^{2} + 11 x + 6 \end{aligned}$ as shown below:
:x+3)(x2+3x+2)=x3+6x2+11x+6)如下所示:

Multiply (x + 3) by (x^2 +3x +2)

Work it Out
::工作出来

Use the method of the last example to expand the cubic functions below:
::使用最后一个示例的方法扩展以下的立方函数 :

$\begin{aligned} \begin{array}{ll} a. & y = (x + 1) (x + 3) (x + 5) \\ b. & y = (x - 1) (x - 3) (x - 5) \\ c. & y = (x + 2)^{3} \\ d. & y = (x - 3) (x^{2} + 3 x + 9) \\ e. & y = (x + 3) (x^{2} - 3 x + 9) \\ f. & y = (3 - x) (2 - x) x \end{array} \end{aligned}$
::ay=(x+3)(x+3)(x+3)(x+3)(x+5)b.y=(x-1)(x-3)(x-3)(x-5)(x-5)c.y=(x+2)3d.y=(x-3)(x2+3+3x+9)e.y=(x+3)(x2-3x+9)f.y=(3-x)(2-x)xx

Expand the cubics from example 1 and problem 1.
::从例1和问题1展开立方体。

Activity 3: Modeling with Cubic Functions
::活动3:以立体函数建模

On a distant planet in a galaxy far away, there are two types of trees: truffle trees and avata trees. Each grows in the shape of a cone. As a truffle tree grows from seed, its radius increases at a rate of 1 meter per year, and so does its height. As an avata tree grows, its radius never changes — right from the beginning, it has a radius of 9 meters. However, the height increases by 1 meter per year.
::在遥远的银河系的一个遥远的星球上,有两种树种:松露树和大树。每棵树以锥形生长。当松露树从种子中生长时,其半径以每年1米的速度增长,其高度也是如此。随着大树的生长,其半径从未改变——从一开始,其半径为9米。然而,高幅每年增加1米。

Interactive
::交互式互动

Use the interactive below to explore the relationship between the volume of each tree and time. A pproximate the year when the volumes are the same. Over what time period does the avata tree have a greater volume than the truffle tree?
::使用下面的交互作用来探索每棵树的体积和时间之间的关系。大约是数量相同的年份。亚瓦塔树的体积在什么时间段比松露树大?

INTERACTIVE

Volume of Trees

Move the slider to grow the two trees and see when the Truffle tree becomes larger than the Avata tree.
::移动滑块以种植这两棵树,然后看Truffle树什么时候变得比Avata树大。

Your device seems to be offline.
Please check your internet connection and try again.

+

Do you want to reset the PLIX?

Yes

No

Example 3-1
::例3-1

Recall the truffle trees and avata trees from the previous interactive. Each grows in the shape of a cone. T he }{3}@$" data-id="14904" data-interlink-id="x-ck12-5qr5fl5g64jlfau0" data-json="eyJkYXRhLWVxdWF0aW9uX2xhdGV4IjogIjxtYXRoPlY9XFxwaXtyfV57MiB9XFxmcmFjeyhoKX17M308L21hdGg+IiwgImRhdGEtcGx1cmFsIjogIiIsICJkYXRhLWRlZmluaXRpb24iOiAiVGhlJTIwdm9sdW1lJTIwb2YlMjBhJTIwY29uZSUyMGlzJTIwZ2l2ZW4lMjBieSUyMHRoZSUyMGZvcm11bGElMjAlM0NtYXRoJTNFJTVDdGV4dCU3QlZvbHVtZSU3RCUyMCUzRCUyMCU1Q2ZyYWMlN0IlNUNwaSUyMCU3QnIlN0QlNUUlN0IyJTdEJTIwaCU3RCU3QjMlN0QlMkMlM0MvbWF0aCUzRSUyMHdoZXJlJTIwJTNDbWF0aCUzRXIlM0QlM0MvbWF0aCUzRSUyMHJhZGl1cyUyQyUyMGFuZCUyMCUzQ21hdGglM0VoJTNEJTNDL21hdGglM0UlMjBoZWlnaHQlMjBvZiUyMGNvbmUuIiwgImRhdGEtaWQiOiAxNDkwNCwgImRhdGEtbGFuZ3VhZ2VJRCI6IDEsICJkYXRhLXRlcm0iOiAidm9sdW1lIG9mIGEgY29uZSJ9" data-languageid="1" data-plural="" data-term="volume of a cone" role="term" tabindex="0"> volume of a cone is given by the equation below. Draw a sketch of a cone and label the dimensions.
::回顾上次互动时的松露树和树。每种树以锥体形状生长。锥体的体积由下面的方程给出。绘制锥体的草图并标出尺寸。

$\begin{aligned} V = \frac{1}{3} π r^{2} h \end{aligned}$

::V=13°r2h

Given that a truffle tree's radius and height increases at a rate of 1 meter per year, in the first year, it has a radius of 1 meter and a height of 1 meter. In the second year, it has a radius of 2 meters and a height of 2 meters. And so on. Create an equation for the volume of a truffle tree as a function of time.
::鉴于松露树的半径和高度以每年1米的速度增加,第一年,其半径为1米,高度为1米。第二年,其半径为2米,高度为2米。等等。根据时间函数,为松露树的体积创建方程式。

Given that an avata tree's radius is always 9 meters and the height increases by 1 meter per year, in the first year, the avata tree has a radius of 9 meters and a height of 1 meter. In the second year, it has a radius of 9 meters and a height of 2 meters. And so on. Create an equation for the volume of a truffle tree as a function of time.
::鉴于阿瓦塔树半径始终为9米,高度每年增加1米,第一年,阿瓦塔树半径为9米,高度为1米。第二年,其半径为9米,高度为2米。等等。根据时间函数,为松露树的体积创建方程式。

What kind of function is each?
::每种功能是什么?

Create a function for the difference between the volume of an avata tree and a truffle tree. Specifically create a function $\begin{aligned} D (x) = T (x) - A (x) . \end{aligned}$ What kind of function is this? What is the practical domain for this function? What are the zeroes? Find them algebraically and by approximation with graphing technology. What is the significance of the zeroes ? What is the significance of the minimum?
::创建一个函数以区分 avata 树和 truffle 树的体积。具体地创建函数 D( x) = T( x)- A( x) 。这是哪种函数? 此函数的实用域是什么? 零是什么? 查找它们的代数和图形化技术的近似值。零的意义是什么? 最小值的意义是什么 ?

Solution:    Let $\begin{aligned} x \end{aligned}$ be the year. The equations for the volume of each as a function of time are shown below. For the truffle tree, the radius in meters and the height in meters is the same as the year. For the avata tree, the radius is a constant 9 meters, and the height in meters is the same as the year. The function for the volume of the truffle tree is cubic. The function for the volume of the avata tree is linear.
::溶解度 : 允许 x 是年份。以时间函数计算每个体积的方程式在下面显示。对于松露树, 以米为单位的半径和以米为单位的高度与当年相同。对于阿瓦塔树, 半径为常数 9 米, 以米为单位的高度与当年相同。松露树的体积函数为立方体。对于松露树, 以米为单位的半径和以米为单位的高度为直线。

$\begin{aligned} \begin{array}{ll} Volume Truffle Tree & Volume Avata Tree \\ T (x) = \frac{1}{3} π x^{2} x & A (x) = \frac{1}{3} (9)^{2} π x \\ T (x) = \frac{1}{3} π x^{3} & A (x) = \frac{81}{3} π x \\ A (x) = 27 π x \end{array} \end{aligned}$

::卷积 Truffle 树树卷卷树树卷卷 Avata Avata 树T(x) = 13xx2xA(x) = 13(9) 922xT(x) = 13xx3A(x) = 813xxA(x) = 27xx

The function for the difference in volumes is shown below. It is possible to factor the function as shown.
::数量差异的函数显示如下。可以按所示因素计算函数。

$\begin{aligned} \begin{array}{l} D (x) = \frac{1}{3} π x^{3} - 27 π x \\ D (x) = π x (\frac{1}{3} x^{2} - 27) \end{array} \end{aligned}$

::D(x) = 13x3- 27xD(x) x(13x2- 27)

To determine the zeroes for this function, use the zero product property as shown below. Notice the second equation is a quadratic.
::为确定此函数的零,请使用下文所示的零产品属性。请注意,第二个方程是一个二次方程。

$\begin{aligned} \begin{array}{ll} First Equation & Second Equation \\ π x = 0 & \frac{1}{3} x^{2} - 27 = 0 \\ x = 0 & \frac{1}{3} x^{2} = 27 \\ x^{2} = 81 \\ x = \pm 9 \\ x = 9 \end{array} \end{aligned}$

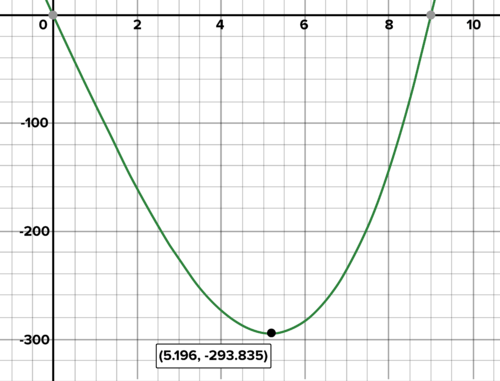
::第一次等量 = 013x2 - 27= 013x2= 013x2= 27x2= 81x= 9x=9

The practical domain for this scenario is $\begin{aligned} [0, \infty) . \end{aligned}$ The graph below shows us that from year 0 to year 9, the difference between the volumes of the truffle tree and avata tree is negative, meaning the truffle tree is smaller than the avata tree. This makes sense because the avata tree starts with a large fixed radius of 9. This was also visible in the interactive. At year 9, the truffle tree has finally grown enough to reach the same dimensions as the avata tree, so the difference between their volumes is 0. Beyond this time, the truffle tree has a greater volume, which means the difference is positive. Using graphing technology, the minimum in the domain is about (5.20, -294). This means the moment that the avata tree has the greatest volume compared to the truffle tree is at about 5.20 years.
::此假想的实际领域是[0,]。下图显示,从0年到9年,松露树和阿瓦塔树的体积差异为负值,这意味着松露树比阿瓦塔树小。这有道理,因为阿瓦塔树开始时的固定半径很大,为9年,这在互动中也可以看到。在9年,松露树最终长到与阿瓦塔树的体积相同,因此其体积差异为0。在这一年之后,松露树的体积更大,这表示差异是正值的。使用图形技术,这个域的最小值是5.20, - 294,这意味着与松露树相比,松露树的体积最大值大约为5.20年。

The difference in volume between truffle trees and avata trees.

Work it Out
::工作出来

Asteroid P-314 is roughly spherical, with a radius of 10 meters in year 0. It's made of ice, and the sun is melting it at so its radius decreases by 1 meter per year. Recall that the volume of a sphere is given by the formula :
::Asteroid P-314 大致是球状的, 0年的半径为10米。它由冰组成, 太阳正在融化, 其半径每年减少1米。回顾一个球体的体积是由公式提供的 :

$\begin{aligned} V = \frac{4}{3} π r^{3} \end{aligned}$

::V=43°r3

Create a function to model the volume of the sphere as a function of time. What is the practical domain for this scenario? Graph the function over the practical domain. What is the significance of the zeroes in the domain? Use graphing technology to determine the relevant zero. Use graphing technology to determine how many years it will take for the volume to decrease by half from its initial volume in year 0. If possible, write and solve equations to determine the solution to the last two questions.
::创建函数, 以时间函数来模拟球体的体积。此方案的实际域是什么? 绘制实用域的函数。域内的零的意义是什么? 使用图形化技术来确定相关的零。使用图形化技术来确定体积比零年的初始体积减少一半需要多少年时间。如果可能的话, 写和解析方程式来确定最后两个问题的解决方案。

The path of a roller coaster over the interval [0,70] is given by the function below. The $\begin{aligned} x \end{aligned}$ -axis represents the path of a horizontal track with a camera on it, and the origin is the point of the first photo. What are the zeroes for this function, and what do they represent in this scenario? Use graphing technology to approximate the highest the roller coaster gets above the camera track over the interval [0,40], and the lowest the roller coaster gets below the camera track over the interval [40,70]. Find any two points on the graph and determine the average over that interval.
::间距 [ / 70] 的过山车路径由下面的函数给定。 x 轴代表水平轨迹路径, 上面有一个相机, 其来源是第一张照片的点。此函数的零是多少, 以及它们在这个假想中代表什么 ? 使用图形技术, 以估计在间距 [ / 40 上方的过山车在相机轨迹上方的高度, 最低的过山车在间隔[ 40 下方的相机轨迹下方 [ 40, 70] 。在图形中找到任何两个点, 并确定该间距的平均值。

$\begin{aligned} P (x) = .01 x (x - 40) (x - 70) \end{aligned}$

::P(x)=.01x(x-40)(x-70)

Give the zeroes for each of the following quadratics. Use substitution to find several additional points. Sketch the graph of each, beginning with the zeroes. Confirm your graph with graphing technology.
::给下方方方块中的每个方块的零。使用替代来查找其他几个点。从零开始, 绘制每个方块的图形。用图形技术确认您的图形。

$\begin{aligned} \begin{array}{ll} a. & y = x (x - 2) (x + 2) \\ b. & y = (x + 3) (4 x - 1) x \\ c. & y = x^{3} + 8 Hint: Write and solve without factoring to find the single zero. \\ d. & y = x^{3} - 2 x^{2} Hint: Factor out a greatest common factor. \\ e. & y = x^{3} - 2 x \\ f. & y = x^{3} + 2 x \end{array} \end{aligned}$
::ay=xx(x- 2)(x+2)(x+2)b.y=(x+3)(4x-1)xc.y=x3+8Hint:在不计号的情况下写入和解答以查找单位 0.d.y=x3-2x2Hint:将最大公因数( y=x3- 2xf.y=x3+2x) 乘以最大公因数。 e.y=x3- 2xf.y=x3+2xx

Interactive
::交互式互动

Use the following interactive to explore changing the zeroes for a cubic. Observe the impact on the maximums and minimums within the graphing window when two or three zeroes merge to become a single zero.
::使用以下互动方式来为立方体探索修改零。当两个或三个零合并成一个零时, 观察对图形窗口内最大和最小值的影响。

INTERACTIVE

Cubic Functions

Move the colored points to explore different zeros for a cubic function.
::移动彩色点以为立方函数探索不同的零。

Your device seems to be offline.
Please check your internet connection and try again.

+

Do you want to reset the PLIX?

Yes

No

Summary
::摘要

Cubics can be used to model scenarios involving volume.
::三次立方体可用于模拟涉及体积的假设情景。

Cubics can be factored to find zeroes.
::可计算三次立方体以找到零。

Use graphing technology to find zeroes for cubics that cannot be factored, or to find maximum and minimum values over an interval.
::使用图形化技术为无法计数的立方体找到零,或在间隔内找到最大值和最小值。

版权所有 © 2024 由瓜瓜科技thewaytolearn.cn设计。保留所有权利。