指数函数和等量

播放段落

In this lesson, you will use to model given scenarios. You'll solve equations involving exponential functions algebraically, and graphically when you find you lack the algebraic tools. You'll develop the algebraic tools to solve exponential equations that you previously solved graphically, and apply those techniques to new problems.
::在此课中, 您将使用模型化给定的假设情景。 您将解析包含指数函数代数的方程式, 当发现您缺少代数工具时, 您将用图形化的方式解析包含指数函数代数函数的方程式。 您将开发代数工具来解析您先前用图形解析的指数方程式, 并将这些方法应用于新问题 。

播放段落

Introduction: Solving Equations Algebraically and Graphically
::导言:用数字和图形形式表示等同

播放段落

Work it Out 
::工作出来

播放段落
1. All but three of the equations below can be solved with algebraic techniques you've already learned. Solve them algebraically. Check your answer by substitution or with technology. Solve the remaining three equations with technology. If possible, identify the type of equation you are solving.
   ::除了以下三个方程式之外, 其余三个方程式都可以用你已经学习过的代数技术来解决。 用代数法解决它们。 请通过替换或技术来检查答案。 用技术来解决剩下的三个方程式。 如果可能的话, 请确定您正在解决的方程式类型 。

播放段落

$\begin{align*}\qquad \quad\begin{array}{ll} \text{a.} & -\frac25 x+\frac34=\frac13\\ \text{b.} & x^2-x-6=0\\ \text{c.} & 3x^2=10\\ \text{d.} & \sqrt{x}=3\\ \text{e.} & \sqrt{x-5}+7=14\\ \text{f.} & (2x-3)^2-7=1\\ \text{g.} & 2x^2=4x+3\\ \text{h.} & \frac{1}{x}=\frac{2}{3}\\ \text{i.} & 3x^2=2x\\ \text{j.} & 2^x=7\\ \text{k.} & \left(\frac12\right) ^ x =\frac{1}{10}\\ \text{l.} & 50(1.14)^x=140\\ \end{array}\end{align*}$
::a.- 25xx+34=13b.x2-x- 6=0c.3x2=10d.x=3e.x-5+7=14f. (2x-3)2- 7=1g.2x2=4x+3h.1x=23i3x2=2xj.2x=7k. (12)x=110l. 50(1.4)x=140

播放段落
2. Theodore invests $400 in an account that earns 6% interest annually. Write and graph an equation for the amount of money in the account as a function of time. How much will Theodore have after 5 years? When will he have 10 times his initial investment?
   ::西奥多在每年赚取6%利息的账户上投资400美元。 以时间函数来写和绘制账户中金额的方程式。 5年后,西奥多将有多少资金? 他何时会有10倍的初始投资?
播放段落
3. Magdalena is comparing accounts. One earns 8% compounded quarterly. Another earns 9% compounded annually. Which is a better investment? Explain your decision.
   ::Magdalena 正在比较账户。 一个人每季收入8 % , 另一人每年收入9 % 。 哪种投资更好? 请解释您的决定 。
播放段落
4. A population of finches on an island numbers 52 in year 0, and increases by 3% every year. How long will it take the population to double? How long will it take the population to increase to 160% of its initial value?
   ::岛屿人口在零岁52岁,每年增长3%。 人口翻一番需要多长时间? 人口增长到最初价值的160%需要多长时间?
播放段落
5. A population of tortoises numbers  $\begin{align*}P\end{align*}$  in year zero, and increases by 3% every year. How long will it take the population to double? How long will it take the population to increase to 160% of its initial value?
   ::乌龟人口在零岁时为P,每年增长3%。 人口翻一番需要多长时间? 人口增长到最初价值的160%需要多长时间?
播放段落
6. How much must be invested at 5% compounded annually in order to return $2000 in 7 years?
   ::7年内要回报两千元,每年必须投入多少投资,再投资5%?
播放段落
7. So far in this lesson, which types of equations required solving with graphing technology? Where was the variable in all these cases? 
   ::到目前为止,在这一教训中,哪些方程式需要用图形化技术加以解决?所有这些情况下的变量在哪里?

---

播放段落

Activity 1: Polynomial Equations that are Sometimes Mistaken for Exponential Equations
::活动1:有时在指数等量中误取的多元等量

播放段落

Example 1-1
::例1-1

播放段落

Many of the equations in the lesson so far featured equations with variables in an exponential position. The following equation has a structure very similar to the exponential equations above, but the exponent has a value of 5. It's not an exponential equation. The variable is part of an expression raised to a power. In fact, the following equation is a polynomial, and it can be solved by isolating  $\begin{align*}r\end{align*}$  using inverse operations . Use inverse operations to solve for  $\begin{align*}r.\end{align*}$
::课程中的许多方程式都包含以指数位置显示变量的方程式。以下方程式的结构与上面的指数方程式非常相似,但引号的值为5。它不是指数方程式。变量是电源表达式的一部分。事实上,以下方程式是一个多元方程式,可以通过使用反向操作孤立 r 来解析。使用反向操作来解析 r。

播放段落

$$\begin{align*}60(1+r)^5-10=170\end{align*}$$
::60(1+r)5-10=170

播放段落

Solution:
::解决方案 :

 

播放段落

$\begin{align*}60(1+r)^5-10&=170  && Given ~ equation\\ 60(1+r)^5&=180 && Adding\\ (1+r)^5&=3 && Dividing\\ 1+r&=\sqrt[5]{3} && The ~inverse~ operation ~of ~raising~ to ~the ~5th~ power ~is ~the ~5th~ root.\\ r&=-1\sqrt[5]{3} && Subtracting\\ r &\approx 0.25 && Approximating\end{align*}$
::60(1+r)5 - 10=170 开源方程式60(1+r)5=180Adding(1+r)5=3Divididi1+r=35 向第五电源的反作用是第5根.r=135

 

播放段落

PLIX Interactive
::PLIX 交互式互动

播放段落

Example 1-2
::例1-2

播放段落

Solve the following using the techniques of the last example. Observe and explain similarities and differences between each. 
::使用最后一个例子的技巧解决下列问题。观察并解释每个例子之间的相似之处和不同之处。

播放段落

Solution:
::解决方案 :

播放段落

The first equation has one solution because  $\begin{align*}\sqrt[3]{-8}=-2.\end{align*}$  This can be confirmed:  $\begin{align*}(-2)^3=8.\end{align*}$  Then, add -1 to get  $\begin{align*}r=-3.\end{align*}$
::第一个方程有一个解决方案,因为-832。 这可以确认-2)3=8。 然后,加上-1以获得r3。

播放段落

The second equation has no solution because  $\begin{align*}\sqrt[4]{-8}\end{align*}$  does not return a real number . There is no real number that can be raised to the 4th power to return a negative result. Raising any real number to an even power returns a positive result (or 0). So an even root of a negative number means no real solution.
::第二个等式没有解决办法,因为 84 不返回一个真实的数字。 不存在可以向第四权力方提出一个真实的数字来返回一个负结果。 将任何实际数字提高到一个偶权力方返回一个正结果( 或 0 ) 。 因此,一个负数字的双根就意味着没有真正的解决办法。

播放段落

The third equation has two solutions.
::第三个方程式有两种解决办法。

播放段落

Work it Out
::工作出来

播放段落
1. How much must you invest at 5% compounded annually if you want $2000 in 7 years?
   ::如果你7年内想要2000美元,每年要投资5%,你还要投资多少?
播放段落
2. If you want to invest $500 and earn $2000 after 7 years, what annual interest rate compounded annually will accomplish that goal?
   ::如果想投资500美元,7年后赚取2 000美元,那么,每年加多少年利率才能实现这一目标?
播放段落
3. If you invest $500 at 9% compounded annually, when will you have $2000?
   ::如果你每年投资500美元,总和为9%,那么你什么时候有2000美元?
播放段落
4. Which of the last three problems were solved algebraically? Which was solved graphically? Why? Describe the type of equations that appeared in the last three problems.
   ::后三个问题中哪一个是代数解决的?哪个是图形解决的?为什么?描述后三个问题中出现的方程式类型。

---

播放段落

Activity 2: Solving Exponential Equations
::活动2:解决指数等号

播放段落

Example 2-1
::例2-1

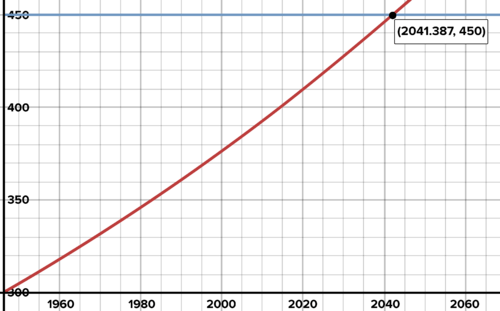
播放段落

The atmospheric concentration of carbon dioxide has been increasing roughly exponentially since measuring began in 1959. At that time, the concentration of atmospheric CO2 was 316 parts per million (ppm). That means that 316 out of every million molecules in the air were CO2 molecules. The concentration in 2016 was 404 ppm. The Paris Agreement seeks to hold atmospheric concentrations of CO2 to below 450 ppm. Use the values for CO2 concentration in 1959 and 2016 to create an equation for the concentration of CO2 a function of the year. Assuming CO2 concentrations continue to increase roughly exponentially, when does your model show the 450 ppm threshold is exceeded? 
::自1959年开始测量以来,大气中二氧化碳的浓度一直在以大约指数增长;当时,大气中的二氧化碳浓度为百万分之316(ppm),这意味着空气中每百万个分子中有316个分子是二氧化碳分子;2016年的浓度为百万分之404 ppm。巴黎协定试图将大气中的二氧化碳浓度保持在百万分之450以下。1959年和2016年,利用二氧化碳浓度值为二氧化碳浓度设定一个当年的函数。假设二氧化碳浓度继续以大约指数增长,当你的模型显示450ppm阈值超过450ppm时?

播放段落

Solution:    For now, think of 1959 as year 0. 2016 is year 57 for the purposes of our model. The initial CO2 concentration was 316 ppm:
::解决方案:目前,将1959年视为0年。 2016年是57年,用于模型目的。 最初的二氧化碳浓度为316 ppm:

播放段落

Since  $\begin{align*}c(57)=404,\end{align*}$   substitute to solve for the annual percent increase,  $\begin{align*}r:\end{align*}$  
::自(57)=404以来,

播放段落

The function for CO2 concentration as a function of the year is:
::作为当年函数的CO2浓度函数为:

播放段落

To shift the function horizontally so that the initial value is returned in the year 1959 instead of year 0:
::水平移动函数,使初始值在1959年而不是第0年返回:

播放段落

To predict when the CO2 concentration reaches 450 ppm:
::预测二氧化碳浓度何时达到450ppm:

播放段落

Example 2-2
::例2-2

播放段落

Radioactive elements decay into other elements or into energy over time. For example, tritium is a radioactive element that decays into helium. But if you have a gram of tritium, it doesn't decay into helium all at once. In a given moment, some atoms of tritium will decay and some won't--which do and which don't is random. And yet, the overall rate of decay is constant , and its measured in terms of the amount of time required for half of the quantity of tritium to decay. This is called the  half-life  of the element. The half-life for tritium is 12.3 days. That means, if you have 8 grams of pure tritium, 12.3 days later you'll have 4 grams, and 12.3 days after that you'll have 2 grams, and so on.
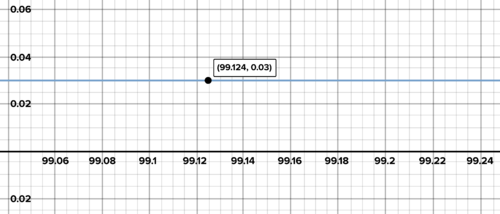
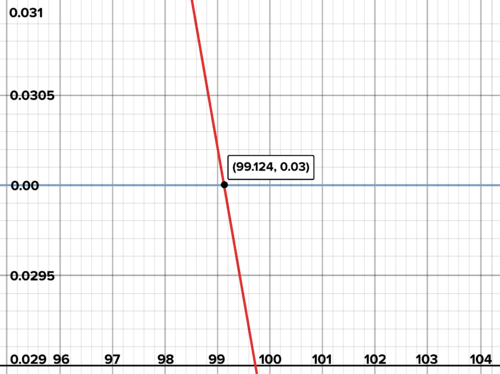
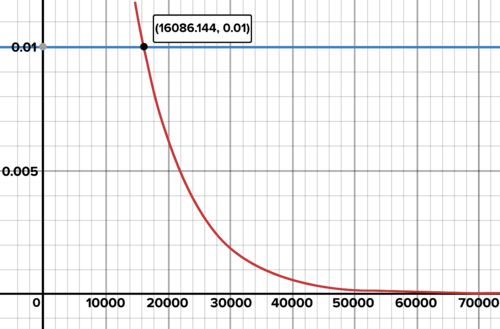
::放射性元素随着时间演变成其他元素或能量。 例如, 是衰变成的放射性元素。 但是, 如果您有一克, 它不会同时腐化成。 在某一时刻, 一些原子会衰变, 有些不会衰变, 有些不会衰变, 并且不是随机的。 然而, 总体衰变速度是恒定的, 其测量速度是: 其衰变所需时间的半衰期。 这就是元素的半衰期。 的半衰期是12.3天。 这意味着, 如果您有8克纯, 12.3天之后, 你就会有4克, 12.3天之后, 12.3天之后, 你就会有2克, 等等。

播放段落

Create an equation for the amount of tritium present as a function of the number of days that have passed. (You've got 8 grams to start with.) Algebraically determine when there is a half gram of tritium and explain each step of your solution method. Use a graph to determine when there are 0.03 grams of tritium.
::创建一个方程式, 计算目前的量, 以计算过去天数的函数 。 (您有 8 克要开始 。) 代数确定当有 半 克 时, 并解释您溶液方法的每一步 。 使用一个图形来确定 0.03 克 。

播放段落

Solution:    The function is exponential, with a multiplier of one-half:
::解答: 函数是指数化的, 乘以半倍数 :

播放段落

The exponent is  $\begin{align*}\frac{x}{12.3}\end{align*}$  so that at 12.3 days, the exponent becomes 1, meaning the initial amount gets halved once. At 24.6 days the exponent becomes 2, so the initial amount gets halved twice, and so on. 
::指数为 x 12. 3 , 这样在12.3 天时,指数变为 1 , 意味着初始金额减半一次。 在24.6天时,指数变为2, 初始金额减半两次, 等等。

播放段落

To determine when there is a half gram of tritium:
::确定何时有半克:

播放段落

This was an unusual and lucky situation, where the expressions on the left and right could be written as expressions with the same base. This enabled us to solve for the exponent.
::这是一种不寻常和幸运的情况,左、右两边的表达方式可以写成以同一基础的表达方式。 这使得我们可以为表率解决问题。

播放段落

To determine when there are 0.03 grams of tritium:
::确定什么时候有0.03克:

播放段落

Here is the graph again with some scaling of the axes that severely distorts the graph but enables you to more clearly see the intersection :
::这里的图表再次显示一些轴的缩放, 这些轴严重扭曲了图形, 但能让您更清楚地看到十字路口 :

播放段落

Work it Out
::工作出来

播放段落

Solve the equations below by creating expressions with the same base.
::通过创建以相同基数为表达式的表达式来解析下面的方程式 。

播放段落

  $\begin{align*}\qquad \quad\begin{array}{ll} \text{a.} & 2^5=2^x\\ \text{b.} & \left(3^2\right)^5=3^x\\ \text{c.} & 9^5=3^x\\ \text{d.} & 5^{\frac{1}{2}}=5^x\\ \text{e.} & \sqrt{5}=5^x\\ \text{f.} & \left(\sqrt[3]{7}\right)^2=7^x\\ \end{array}\end{align*}$  
::a.25=2xb.(32)5=3xc.95=3xc.95=3xd.512=5xe.5=5xf.(73)2=7x

---

播放段落

Activity 3: Modeling Growth and Decay, and Solving Related Equations
::活动3:模拟增长和衰减以及解决相关等量

播放段落

Example 3-1
::例3-1

播放段落

The of radioactive elements functions like a clock. If you have 8 grams of tritium and half of it decays, then 12.3 days have passed. All living plants and animals have radioactive elements in them. One such radioactive element is carbon-14 (C-14). There's not a lot of C-14 in the world, just 75 tons on the entire planet! But more is produced in the atmosphere every day, so the proportion stays roughly constant. 
::放射性元素的功能像钟一样。 如果你有8克,其中一半会腐烂, 那么12.3天已经过去。 所有活的动植物都有放射性元素。 其中之一是碳-14(C-14)。 世界上没有太多的C-14(C-14), 整个星球上只有75吨。 但是,在大气中,每天产生的数量更多, 所以比例基本保持不变 。

播放段落

Because plants take in CO2 from the atmosphere and animals eat plants, all living things have the same proportion of C-14 in them. A 70-kilogram human has about 0.07 micrograms of C-14 in his body. 
::由于植物从大气中吸收二氧化碳,动物吃植物,所有生物都具有与C-14相同的比例。 70公斤的人类体内大约有0.07微克的C-14。

播放段落

When a living thing dies, it stops replenishing its supply of C-14 from the atmosphere, and any C-14 in the animal or plant slowly decays to nitrogen. The half-life of C-14 is 5730 years. If an animal or plant gets preserved in permafrost or a bog, the C-14 in it is like a clock, measuring the amount of time that's passed since it died. This is one way scientists estimate the age of things they excavate from the earth.
::当活物死后,它停止从大气中补充C-14, 动物或植物中的任何C-14逐渐衰减为氮。 C-14的半衰期是5730年。如果动物或植物被保存在永久冻土或沼泽中, C-14就像一个钟, 测量它死后所花的时间。这是科学家估计它们从地球上挖掘出来的事物的年代的一种方法。

播放段落

Scientists excavate the body of a giant ground sloth from the permafrost in Siberia. Its mass is estimated at 70 kilograms. This means that before it died, it had about 0.07 micrograms of C-14 in its body. The scientists measure the current amount of C-14 at 0.01 micrograms. How many years ago did the sloth die?
::科学家们从西伯利亚的永久冻土中挖掘出一个巨大的地洞。 其质量估计为70公斤。 这意味着在它死前, 它体内大约有0.07微克的C-14。 科学家们测量到目前C-14的含量是0.01微克。 多少年前, 针子死了?

播放段落

Solution:    The initial value is 0.07 micrograms. This decreases by half every 5730 years:
::解决方案:初始值为0.07微克。每5730年减少一半:

播放段落

Note that the exponent features the fraction  $\begin{align*}\frac{x}{5730}.\end{align*}$  This is so that when 5730 is substituted for  $\begin{align*}x,\end{align*}$  the exponent becomes 1, resulting in a single halving of the initial value.
::注意前言中含有分数 x5730。 这样, 当 5 730 取代 x 时, 前言变为 1 , 结果是初始值的一分之一半 。

播放段落

To determine the number of years required to reduce the C-14 to 0.01 micrograms:
::为确定将C-14至0.01微克所需的年数:

播放段落

Work it Out
::工作出来

播放段落
1. A sabertooth tiger is excavated from a desert in Utah. Based on its mass, scientists estimate that the tiger had 0.2 micrograms of C-14 in its body when it was alive. Now it has 0.03 micrograms. Determine how long ago the tiger died.
   ::从犹他州的沙漠中挖掘出一只神圣的老虎。根据它的质量,科学家估计老虎活着时身体里有0.2微克的C-14。现在它有0.03微克。确定老虎死了多久。
播放段落
2. A scientist has 50 grams of tritium. How long until there are only 5 grams left?
   ::科学家有50克,还剩5克吗?
播放段落
3. Currently, there are 7.442 billion people living on the planet. The population is growing roughly exponentially, at a rate of 1.12% per year. If the trend continues, what will the population be 20 years from now? 50 years from now? When will the population double
   ::目前,地球上有74.42亿人生活在地球上,人口以每年1.12%的速率增长,大约成倍增长。 如果这一趋势继续下去,20年后的人口会是多少?50年后的人口会是多少?什么时候人口会翻一番?
播放段落
4. What interest rate compounded annually grows $600 to $4,000 in 10 years?
   ::在10年内,何种利率每年增加600美元到4 000美元?
播放段落
5. What initial investment at 7% compounded monthly returns a million dollars in 20 years?
   ::哪些初始投资为7%的复合月回报 20年中100万美元?
播放段落
6. An initial investment is placed in an account that returns 5% compounded continuously. When will its value triple? (Recall that continuous compounding is modeled by  $\begin{align*}y=Pe^{rt}.)\end{align*}$
   ::初始投资被放置在一个账户中,该账户将持续返回 5% 的复合 。 其价值何时会达到 3 倍 ? (提醒注意连续复合是由 Y = Pert 模拟的 y = Pert 。 )

---

播放段落

Activity 4: Solving Exponential Equations with Logarithms
::活动4:用对数解决指数等同

播放段落

You currently have two methods for solving exponential equations:
::您目前有两种解答指数方程式的方法:

播放段落
1. Use graphing or solving technology to solve the equation.
   ::使用图形化或解析技术解析方程式。
播放段落
2. Modify one or both sides of the equation until each side is an exponential expression with the same base.
   ::修改方程式的一面或两面,直到每一面都是以同一基数的指数表达式。

播放段落

The second option can only be used in limited cases. In the following example, you will learn about a third option that you can always use to solve exponential equations algebraically.
::第二个选项只能在有限的情况下使用。 在下面的例子中, 您将了解第三个选项, 您总是可以用来解析指数方程式代数 。

播放段落

Example 4-1
::例4-1

播放段落

Here is a simple exponential equation:
::以下是简单的指数方程式 :

播放段落

This equation is a way of expressing the question: What  value must 2 be raised to in order to return 5? The answer is more than 2, because $\begin{align*}2^2=4.\end{align*}$  It's also less than 3 because  $\begin{align*}2^3=8.\end{align*}$  But guessing isn't going to get you very far.
::这个等式是表达问题的一种方式: 返回 5 需要2 的值是多少? 答案是 2 以上 , 因为 22 = 4 。 也小于 3 , 因为 23 = 8 。 但猜想并不能让你走很远 。

播放段落

Solution:    With many operations, there is an inverse operation that you've learned:
::解决方案:通过许多操作, 有一种逆向操作, 你学到了:

播放段落
• The inverse operation of multiplying by 2 is multiplying by a half.
  ::乘以2的反向作用是乘以半。
播放段落
• The inverse operation of adding 3 is subtracting 3.
  ::增加3的反作用是减去3。
播放段落
• The inverse operation of squaring is square rooting.
  ::隔断的反作用是平方根。
播放段落
• The inverse operation of cube rooting is cubing.
  ::立方体根基的反向操作是孵化。

播放段落

You need an inverse operation for exponentiation, that is, an inverse operation of raising a base to a variable power. That inverse operation is called the  logarithm .  Look at the equation again:
::您需要一个反推法操作, 也就是说, 将基数提升到变量功率的反函数操作。 反函数操作被称为对数。 再看看方程 :

播放段落

$$\begin{align*}2^x=5\end{align*}$$  
::2x=5

播放段落

Read the following statements aloud, and make sense of them in the context of the equation above. They are each expressing the same idea:
::阅读以下声明,并结合上述等式加以理解。

播放段落
• $\begin{align*}x\end{align*}$  is the power that 2 must be raised to in order return 5.
  ::x 是返回 5 的 2 个必须 提升到 5 个 的 权力 。
播放段落
• $\begin{align*}x\end{align*}$  is the result of the inverse operation of exponentiation, with base 2, of 5.
  ::x 是以 5 基数 2 为基数的反推操作的结果 。
播放段落
• $\begin{align*}x\end{align*}$  is the logarithm, with base 2, of 5.
  ::x 是对数, 基数 2 为 5 。
播放段落
• $\begin{align*}x\end{align*}$  is the logarithm, base 2, of 5.
  ::x 是5 的对数, 基数 2 。
播放段落
• $\begin{align*}x\end{align*}$  is the log, base 2, of 5.
  ::x 是日志, 基数 2, 以 5 为基数 。
播放段落
• $\begin{align*}x=\log_{2}{5}\end{align*}$  
  ::x =log2 @% 5
播放段落
• $\begin{align*}x\approx 2.32\end{align*}$  
  ::2.32

播放段落

PLIX Interactive
::PLIX 交互式互动

播放段落

Work it Out
::工作出来

播放段落
1. Solve each of the following by writing the solution as a logarithm. Then use a calculator to approximate the solution. An example is provided.
   ::以对数写成解析法来解析以下各点。 然后使用计算器来接近解析法。 举一个例子 。

播放段落

$$\begin{align*}\begin{array}{l|l} \text{Equation} & \text{Explanation.}\\ \hline 5(2.4)^x+7=92 & \text{Given equation.}\\ 5(2.4)^x=85 & \text{Subtraction.}\\ (2.4)^x=17 & \text{Division.}\\ x=\log_{2.4}{17} &x~ \text{is the power 2.4 must be raised to in order to return 17.}\\ & x\text{ is the log, base 2.4, of 17.}\\ x\approx 3.24 & \text{Calculator to approximate solution.} \end{array}\end{align*}$$   $\begin{align*}\begin{array}{ll} \text{a.} & 2^x=7\\ \text{b.} & 3^x=5\\ \text{c.} & 4^x=0.1\\ \text{d.} &\left(\frac12\right)^x=0.1\\ \text{e.} & 100\left(\frac12\right)^x=40\\ \text{f.} & 300(1.15)^x=800\\ \text{g.} & P(1.04)^x=2P\\ \text{h.} & 200(1.01)^{\frac{x}{3}}=400\\ \text{i.} & 2^{1000}=2^x\\ \end{array}\end{align*}$
::EquationExplanation.5(2.4)x+7=92Felentn 方程式5.(2.4)x=85 suctractition.(2.4)x=17 Discription.x=17.x=log2.4=17x17x2.4=24x是返回电源2.4必须提高的电源。A.2x=7b.3x=5c.4x=0.1d.(12)x=0.1e.100(12)x=40f.300(1.15x=800g.P(1.04)x=2Ph.200(1.01)x3=400i.21000=2x

播放段落
2. Use the definition of the logarithm to compute each of the following without a calculator:
   ::使用对数定义来计算没有计算器的以下每一种:

播放段落

$\begin{align*}\begin{array}{ll} \text{a.} & \log_{2}{8}\\ \text{b.} & \log_{3}{9}\\ \text{c.} & \log_{5}{5}\\ \text{d.} & \log_{\frac12}{\frac18}\\ \text{e.} & \log_{2}{\frac{1}{16}}\\ \text{f.} & \log_{2}{1}\\ \text{g.} & \log_{2}{\frac12}\\ \text{h.} & \log_{2}{\frac14}\\ \text{i.} & \log_{3}{\frac{1}{81}}\\ \end{array}\end{align*}$
::288b.log39c.log5_5d.log12_18e.log2_116f.log2_1g.log2_12h.log2_14i.log3_181

播放段落
3. The amount of C-14 in a mammoth when it was living was 1.2 micrograms. Now it is 0.25 micrograms. Determine algebraically how long ago the mammoth died.
   ::活在长毛象中的C-14值为1.2微克,现在为0.25微克。确定长毛象多久前死亡的代数。
播放段落
4. Create a compound interest problem whose solution requires logarithms. Solve the resulting equation.
   ::创建复利问题, 其解决方案需要对数。 解决由此产生的方程式 。
播放段落
5. Create a C-14 problem whose solution requires logarithms. Solve the resulting equation.
   ::创建 C-14 问题, 其解决方案需要对数。 解析产生的方程式 。
播放段落
6. Create an scenario involving the population of an animal on an island. Create a problem whose solution requires logarithms. Solve the resulting equation.
   ::创建一个涉及岛上动物种群的假设情景。 创建一个需要对数解决的问题。 解决由此产生的方程式 。