平板的变换
章节大纲
-
Transformation is a process that changes the shape, size or position of a figure to create a new image. It is a function that takes points in the plane as inputs and gives other points as outputs. You can think of a transformation as a rule that tells you how to create new points.
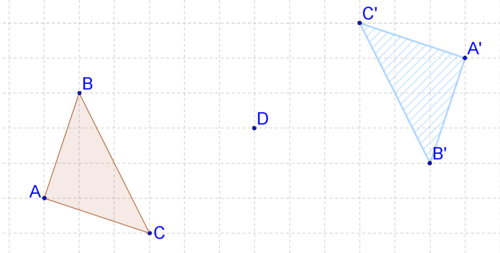
::转换是一个改变图的形状、 大小或位置以创建新图像的过程。 它是一个函数, 将平面中的点作为输入点, 并将其他点作为输出点。 您可以将转换视为一条规则, 告诉您如何创建新点 。Suppose you have a transformation that applies a horizontal stretch factor of two to each point . Below, this transformation is applied to triangle to create triangle
::假设您有一个变换 F, 将水平伸展因子为 2 应用到每个点。 下面, 此变换将应用到三角 S 上, 以创建三角 S 。-
is considered the image of
by
::S ' 被视为F的S 图像。 -
It is also correct to
say that
maps
to
::说F向S-S-地图也是正确的。 -
Each of the points in the image are labeled with a
symbol, which is read as "prime."
::图像中的每一个点都贴上符号的标签, 符号被读为“ 原始 ” 。
This helps to show how points on correspond to points on For example, you could say that "point maps to point -prime."
::这有助于显示 S 上的点与 S 的点对应。 例如, 您可以说“ A 点地图 指向 A 点 ” 。Some transformations preserve length and angles . Preserving length means that if a line segment is 3 units, its image will also be 3 units. Similarly, preserving angles means if an angle is its image will also be
::有些变形保留长度和角度。 保留长度意味着如果一个线段为3个单位, 其图像也将是3个单位。 同样, 保存角度意味着如果一个角度为60度, 其图像也将是60度 。-
A transformation that preserves length and angles is called a rigid transformation.
::保持长度和角度的变换 被称为僵硬变换
Recognizing Rigid Transformations
::硬硬变换1. Is a horizontal stretch an example of a rigid transformation?
::1. 横向伸展是否是僵硬转变的一个例子?No. You can prove this using the picture above by showing that length is not preserved .
::否。您可以通过显示长度未保留来用以上图片来证明这一点。2. A transformation reflects points in shape across to create shape . Is this reflection a rigid transformation?
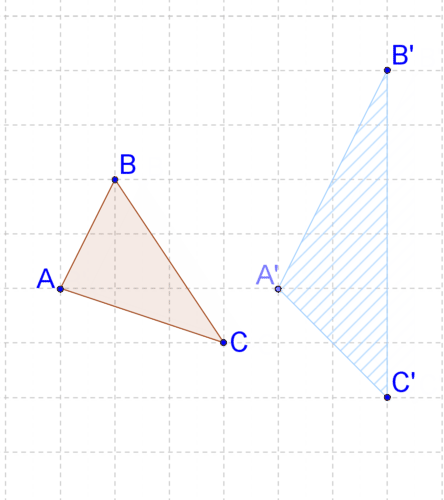
::2. 转换反映了横跨AB的K型形状,以形成K形形状。Yes, reflections are rigid transformations. You can verify that the distances between the points are preserved.
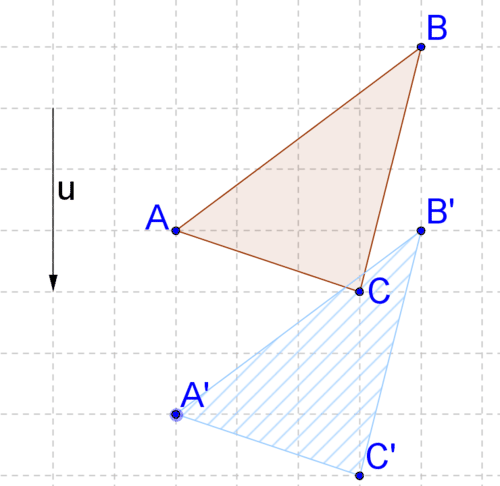
::是的,反射是僵硬的变形。你可以验证点之间的距离是否保持。3. A transformation translates points in shape along vector to create shape Is this translation a rigid transformation?
::3. 转换将矢量 v 上的 K 形状的点转换为形状, 以创建 K 形状 。 这是否翻译为刻板的转换 ?Yes, translations are rigid transformations. You can verify that the distances between the points are preserved.
::是的,翻译是硬质转换。 您可以验证点之间的距离是否被保存 。
Examples
::实例实例实例实例Example 1
::例1You slide a book across your desk. You pour soda from a can into a big glass. Describe these actions as transformations.
::你把一本书滑过桌子。你把苏打水从罐子倒到一个大杯子。把这些动作描述为转换。Sliding a book across your desk is a rigid transformation because a book is a rigid object that does not change shape. The distances and angles that make up the book don't change once the book is in a new location. Pouring soda, on the other hand, is not a rigid transformation. Liquid is not a rigid object and it can change shape depending on its surroundings. The overall shape of the soda in the can will be different from the overall shape of the soda in the glass.
::在您的办公桌上滑动一本书是一个僵硬的转换, 因为一本书是一个不改变形状的僵硬对象。 构成这本书的距离和角度一旦在新位置, 就不会改变。 另一方面, 投注苏打水并不是一个僵硬的转换。 液体不是一个僵硬的物体, 它可以根据周围环境改变形状。 罐中苏打水的整体形状将与玻璃中苏打水的整体形状不同 。Example 2
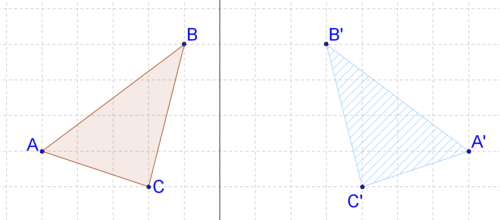
::例2A transformation rotates points in shape around point to create shape Does this rotation look like a rigid transformation? Use algebra to prove your answer.
::转换旋转点在 D 点周围的形状 K 旋转点以创建形状 K 。 此旋转看起来像是僵硬的变换吗? 使用代数来证明您的回答 。This appears to be a rigid transformation.
::这似乎是一种僵硬的转变。With the Pythagorean Theorem , you can show that the corresponding sides are the same length . For example:
::Pytagorean Theorem, 您可以显示对应的两边长度相同。 例如 :
::AC =32+22=9+4=13 单位的长度
::A{C}32+22=9+4=13单位的长度
::因此,这确实是一种僵硬的转变。Example 3
::例3What makes a transformation a rigid transformation?
::改变是什么使僵硬的转变?Rigid transformations preserve distance and angles. All corresponding sides will be the same length and all will be the same measure .
::硬质变换保持距离和角度。 所有对应的侧面的长度都相同, 大小都相同 。Summary -
Transformation
is a process that changes the shape, size, or position of a figure to create a new image.
::变换是一个进程, 改变图的形状、 大小或位置, 以创建新图像 。 -
A transformation F can apply a horizontal stretch factor to a figure, such as triangle S, to create a new image, triangle S'.
::变换 F 可以对数字, 如三角 S , 应用水平伸缩系数来创建新图像, 三角 S 。 -
Points in the new image are labeled with a ' symbol, read as “prime,” to show correspondence between points in the original figure and the transformed image.
::新图像中的点标有符号,称为 " 主要 " ,以显示原图中点与变形图像之间的对应。 -
Rigid transformations
are those that preserve length and angles.
::坚硬的变形是那些保持长度和角度的变形。 -
Transformations that cause stretching are not rigid transformations, as they do not preserve length.
::造成伸展的变形不是僵硬的变形,因为它们不会保持长度。
Review
::审查审查审查审查For 1-7, define each statement as true or false.
::第1至7条,将每一说法定义为真实或虚假。1. Translations are rigid transformations.
::1. 翻译是僵硬的转换。2. Rotations are rigid transformations.
::2. 轮调是僵硬的变换。3. Horizontal stretches are rigid transformations.
::3. 横向拉伸是硬质变换。4. Rigid transformations preserve location in the plane.
::4. 硬质变换保留飞机的位置。5. Corresponding sides in rigid transformations are the same length.
::5. 僵硬转型中的对应方长度相同。6. If it's not a rigid transformation, it's not a real transformation.
::6. 如果不是僵硬的转变,也不是真正的转变。7. Reflections are rigid transformations.
::7. 反思是僵硬的转变。Use the following image for 8-9.
::8- 9 时使用以下图像 。8. Describe the transformation in your own words. Does it look like a rigid transformation?
::8. 用你自己的话描述这种转变。它看起来像是僵硬的转变吗?9. Prove your answer to #8 by comparing the lengths of two sides.
::9. 通过比较两边的长度来证明你对8号的回答。Use the following image for 10-11.
::10-11 使用以下图像 。10. Describe the transformation in your own words. Does it look like a rigid transformation?
::10. 用你自己的话描述这种转变,它看起来像是僵硬的转变吗?11. Prove your answer to #10 by comparing the lengths of two sides.
::11. 通过比较两边的长度来证明你对10号的回答。Use the following image for 12-13.
::12-13 使用以下图像 。12. Describe the transformation in your own words. Does it look like a rigid transformation?
::12. 用你自己的语言描述这种转变。它看起来像是僵硬的转变吗?13. Prove your answer to #12 by comparing the lengths of two sides.
::13. 通过比较两边的长度来证明你对12号的回答。Use the following image for 14-15.
::14-15 使用以下图像 。14. Describe the transformation in your own words. Does it look like a rigid transformation?
::14. 用你自己的话描述这种转变,它看起来像是僵硬的转变吗?15. Prove your answer to #14 by comparing the lengths of two sides.
::15. 通过比较两边的长度来证明你对14号的回答。16. A transformation can be thought of as a movement of an object in a plane such that angle measures and segment lengths are preserved. Imagine a triangle that you've cut out, lying flat on a piece of poster paper. How can the triangle be moved so that the measures of angles and the lengths of segments are preserved? How can the different types of movements be categorized and defined? Be creative. Draw, write, and discuss how to more specifically describe and define the types and methods of rigid motion transformations.
::16. 转换可被视为在平面上物体的移动,以便保持角度量和区段长度; 想象一个三角形,你已经切割出来,躺在一张海报纸上; 如何移动三角形,以便保持角度和区段长度的测量; 如何分类和定义不同类型的移动? 具有创造性; 绘制、 撰写和讨论如何更具体地描述和界定僵硬运动变换的类型和方法。17. There is one type of rigid motion transformation which seems to require the triangle described above to be lifted from the poster board and flipped. (Mathematically, that's not what happens, but it looks that way from our 3-dimensional perspective.) How can this transformation be defined and described?
::17. 有一种僵硬的运动转变似乎要求从海报板上吊起上述三角形并翻转。 (从数学角度讲,这不是发生的事情,但从我们的三维角度来看,它看起来是这样。 )如何定义和描述这种转变?18. Sometimes we can describe transformations in the coordinate plane. For example, one can specifically alter the coordinates of the vertices of a polygon according to a rule. Think about how you can modify the coordinates of a point and what the consequences of each type of modification would be. Experiment. Draw a polygon on a coordinate plane, and alter the coordinates according to different rules, then draw the resulting images. Write about and discuss your conclusions.
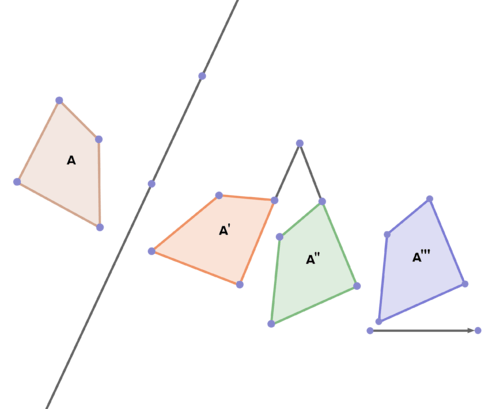
::18. 有时我们可以描述坐标平面的变形,例如,可以按照规则具体改变多边形顶点的坐标。想想如何修改点的坐标以及每一种修改的后果。实验。在坐标平面上绘制多边形,并根据不同的规则修改坐标,然后绘制产生的图像。写和讨论你的结论。19. Define and describe the transformations that map A to A' to A'' to A''' below.
::19. 定义和描述地图A至A的变换。20. Some of the images below represent rigid motion transformations of polygon B and some do not. Decide which do and which don't, and explain your choices. Define and describe the ones that do.
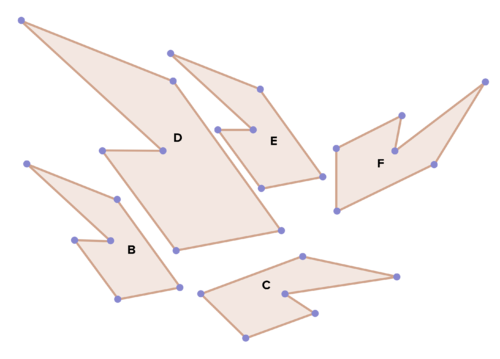
::20. 下面的一些图像代表多边形B的僵硬运动变形,有些则不。决定哪些是,哪些是,哪些是,哪些不是,并解释你的选择。定义和描述哪些是。Review (Answers)
::审查(答复)Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。 -
is considered the image of
by