关于线和角的定理

播放段落

Consider two parallel lines that are intersected by a third line .  That third line is called  a transversal , and when it crosses the two others, many different angle pairs are formed. If the two lines are parallel , as they are in the interactive image below, these angle pairs have special properties. 
::考虑由第三行交叉的两条平行线。第三行被称为横向线,当它横跨另外两条线时,会形成许多不同的角度对。如果这两条线是平行的,就像下面交互图像中那样,这些角度对具有特殊的属性。

播放段落

All Angles
::全部角

播放段落
• Corresponding angles   are called that because their locations correspond: they are formed on different lines but in the same position. They also 'face' the same direction.  E xamples of corresponding angle pairs are $\begin{array}{r}\mathrm{\angle }1\end{array}$    and $\begin{array}{r}\mathrm{\angle }5,\end{array}$   $\begin{array}{r}\mathrm{\angle }2\end{array}$ and $\begin{array}{r}\mathrm{\angle }6\end{array}$ , $\begin{array}{r}\mathrm{\angle }3\end{array}$ and $\begin{array}{r}\mathrm{\angle }7\end{array}$ , and $\begin{array}{r}\mathrm{\angle }4\end{array}$ and $\begin{array}{r}\mathrm{\angle }8.\end{array}$  
  ::相应的角度被命名为相应的角度, 因为它们的位置对应: 它们由不同的线条组成, 但位置相同 。 它们也以相同的方向“ 脸 ” 。 相应的角对的例子有 1 和5 、 2 和 6 、 3 和 7 、 4 和 8 。

播放段落
• Same side interior angles  (sometimes called consecutive interior angles ) are on the  interior of the figure ( between the parallel lines) and on the same side of the transversal . The same side interior angle pairs in this figure are $\begin{array}{r}\mathrm{\angle }4\end{array}$   and $\begin{array}{r}\mathrm{\angle }5,\end{array}$   and  $\begin{array}{r}\mathrm{\angle }3\end{array}$ and $\begin{array}{r}\mathrm{\angle }6.\end{array}$
  ::同侧内角(有时称为连续内角)位于图的内侧(平行线之间)和横向的同一侧面。此图中的同侧内角对齐为++4和+5,以及+3和+6。
播放段落
• Alternate interior angles  are also  on the interior of the figure,   but on opposite sides of the transversal.  The alternate interior angle pairs here are $\begin{array}{r}\mathrm{\angle }3\end{array}$  and $\begin{array}{r}\mathrm{\angle }5,\end{array}$  and  $\begin{array}{r}\mathrm{\angle }4\end{array}$ and $\begin{array}{r}\mathrm{\angle }6.\end{array}$
  ::替代内角也位于图的内侧, 但位于横向的对面。 这里的替代内角对齐是 3 和 5 , 4 和 6 。
播放段落
• $\begin{array}{r}\mathrm{\angle }1\end{array}$ and $\begin{array}{r}\mathrm{\angle }7\end{array}$ are alternate exterior angles .  Exterior angle pairs are on the exterior of the figure (above and below the parallel lines). Another example of is $\begin{array}{r}\mathrm{\angle }2\end{array}$ and $\begin{array}{r}\mathrm{\angle }8.\end{array}$  
  ::\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\8\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\8\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\
播放段落
• $\begin{array}{r}\mathrm{\angle }2\end{array}$ and $\begin{array}{r}\mathrm{\angle }7\end{array}$ are same side exterior angles  (sometimes consecutive exterior angles ). If lines are parallel, then same side exterior angles are supplementary. Another example of same side exterior angles is $\begin{array}{r}\mathrm{\angle }1\end{array}$ and $\begin{array}{r}\mathrm{\angle }8.\end{array}$  
  ::\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\

---

播放段落

Corresponding Angles
::对应的角

播放段落

Each angle created by the transversal and the top line has a corresponding angle with an angle created by the transversal and the bottom line.  You can see the  corresponding angle pairs color-coded, using the interactive diagram above (if the diagram is all grey, click the small white arrow in the blue box next to the diagram). How do you think these compare to each other ?
::由横贯和上线创建的每个角度都有相应的角度, 由横贯和底线创建一个角度。 您可以使用上面的交互式图表( 如果图表都是灰色的, 请单击图旁边的蓝框中的小白箭头) 来看到对应的角度对面的颜色编码 。 您如何看待这些对比 ?

播放段落

Your intuition and knowledge of translations might correctly suggest that these angles are congruent . Imagine translating one of the angles along the transversal until it meets the second parallel line. It will match its corresponding angle exactly. This is known as the
::您对翻译的直觉和知识可能正确地表明这些角度是相似的。 想象一下将一个角度沿横向翻译, 直到它与第二条平行线相匹配。 它会与相应的角度完全吻合。 这被称为“ ” 。

播放段落
• Corresponding Angle Postulate : If two parallel lines are cut by a transversal, then the corresponding angles are congruent.
  ::对应的 角度 假设 : 如果两个平行线由横向线切除, 那么相应的角度是相似的 。

播放段落

Remember that a postulate is a statement that is accepted as true without proof. Your knowledge of translations should convince you that this postulate is true.
::记住, 假设是一个被接受为真实的声明, 没有证据。 您对翻译的知识应该使您相信这个假设是真实的 。

---

播放段落

Vertical Angles are Congruent
::垂直角度为 Congruent

播放段落

Recall that are pairs of opposite angles created by intersecting lines . Prove that vertical angles are congruent.
::回想那些由交叉线所创造的相反角度的对。 证明垂直角度是相容的 。

播放段落

For this proof, you are not given a specific picture. When not given a picture, it helps to create a generic picture to reference in your proof. It's important that the picture does not include any information that you cannot assume. Below is a generic picture of intersecting lines with angles numbered for reference.
::对于此证明, 您没有给您提供具体图片。 没有给您提供图片, 它会帮助创建您在证明中引用的通用图片 。 重要的是图片不包含您无法假定的任何信息 。 下面是带有用于引用的角度的交叉行的通用图片 。

播放段落

In this picture, $\begin{array}{r}\mathrm{\angle }1\end{array}$ and $\begin{array}{r}\mathrm{\angle }2\end{array}$ are vertical angles. Your job is to prove that $\begin{array}{r}\mathrm{\angle }1\cong \mathrm{\angle }2\end{array}$ . You can use any style of proof you prefer. Given below is a two-column proof.
::在此图片中, 1 和 2 是垂直角度。 您的工作是证明 1 2 。 您可以使用您喜欢的任何类型的证明 。 以下给出两栏证明 。

播放段落 Statements ::声明声明 声明 声明 声明 声明 声明 声明 声明 声明 声明 声明 声明 声明 声明 声明 声明 声明 声明 声明 声明	播放段落 Reasons ::原因原因原因原因
播放段落 $\begin{array}{r}m\mathrm{\angle }1+m\mathrm{\angle }3={180}^{\circ }\end{array}$ and $\begin{array}{r}m\mathrm{\angle }2+m\mathrm{\angle }3={180}^{\circ }\end{array}$ ::m1+m3=1802+m3=180	播放段落 Two angles that form a line are supplementary ::构成线条的两个角度是补充的
$\begin{array}{r}m\mathrm{\angle }1+m\mathrm{\angle }3=m\mathrm{\angle }2+m\mathrm{\angle }3\end{array}$	播放段落 Algebraic substitution ::代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代代
$\begin{array}{r}m\mathrm{\angle }1=m\mathrm{\angle }2\end{array}$	播放段落 Subtraction property of equality ::平价减价财产
$\begin{array}{r}\mathrm{\angle }1\cong \mathrm{\angle }2\end{array}$	播放段落 If two angles have the same measure , they are congruent. ::如果两个角度的量度相同,它们就是相同的。

播放段落

Vertical angles are congruent is a theorem . Now that it has been proven, you can use it in future proofs without proving it again.
::垂直角度是一致的, 是一个定理。 既然已经证明了这一点, 您可以在未来的证据中使用它, 而不再次证明它 。

---

播放段落

Alternate Interior Angles are Equal
::替代的内地角度相等

播放段落

When two parallel lines are cut by a transversal, two pairs of are formed. In the diagram below, $\begin{array}{r}\mathrm{\angle }3\end{array}$ and $\begin{array}{r}\mathrm{\angle }5\end{array}$ are alternate interior angles. Similarly, $\begin{array}{r}\mathrm{\angle }4\end{array}$ and $\begin{array}{r}\mathrm{\angle }6\end{array}$ are alternate interior angles. 
::当两条平行线被横切时,将形成两对平行线。在下图中,%3和%5是不同的内部角度。同样,%4和%6是不同的内部角度。

播放段落

Prove that if two parallel lines are cut by a transversal, alternate interior angles are congruent.
::证明如果两条平行线被横切切开, 不同的内部角度是相似的 。

播放段落

Use the diagram above, and prove that $\begin{array}{r}\mathrm{\angle }3\cong \mathrm{\angle }5\end{array}$ . (The same exact proof would show that $\begin{array}{r}\mathrm{\angle }4\cong \mathrm{\angle }6\end{array}$ ). Again, in general you can use any style of proof that you prefer. Here is a paragraph proof.
::使用上面的图表, 并证明% 3 @% 5。 (同样确切的证据将显示% 4 @% 6) 。 一般来说, 您可以使用您喜欢的任何类型的证明 。 下面是段落的证明 。

播放段落

$\begin{array}{r}\mathrm{\angle }1\cong \mathrm{\angle }3\end{array}$ because they are vertical angles and vertical angles are always congruent. $\begin{array}{r}\mathrm{\angle }1\cong \mathrm{\angle }5\end{array}$ because they are corresponding angles created by parallel lines and corresponding angles are congruent when lines are parallel. $\begin{array}{r}\mathrm{\angle }3\cong \mathrm{\angle }5\end{array}$ because if two angles are congruent to the same angle, they are congruent to each other by the transitive property .
::13 因为它们是垂直角度, 垂直角度总是相同的。 @15 因为它们是平行线所创造的相应角度, 当线是平行线时相应的角度是相同的。 @35 因为如果两个角度与同一角度一致, 它们彼此的过渡属性是相同的 。

播放段落

*Note: The transitive property states that if two objects are equal/congruent to the same third object, then they are equal/congruent to each other. The transitive property is a form of substitution. You can use it in any proof.
::* 注:过渡性财产规定,如果两个物体相等/相容于同一个第三个物体,那么它们彼此平等/相容。过渡性财产是一种替代形式,可以在任何证据中使用。

播放段落

If two parallel lines are cut by a transversal, then alternate interior angles are congruent is a theorem . Now that it has been proven, you can use it in future proofs without proving it again.
::如果两条平行线被横切切开,那么其他内部角度是相同的则是一个定理。既然已经证明了这一点,您可以在以后的证明中使用,而不必再次证明。

---

播放段落

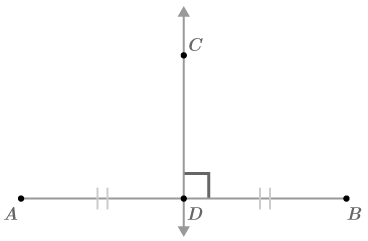
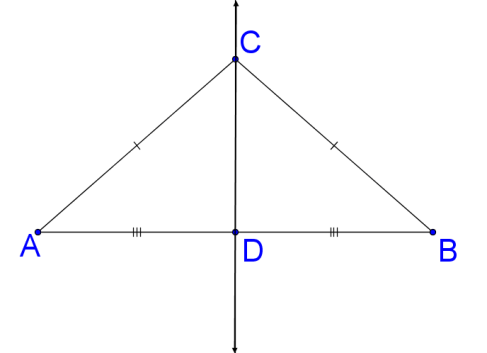
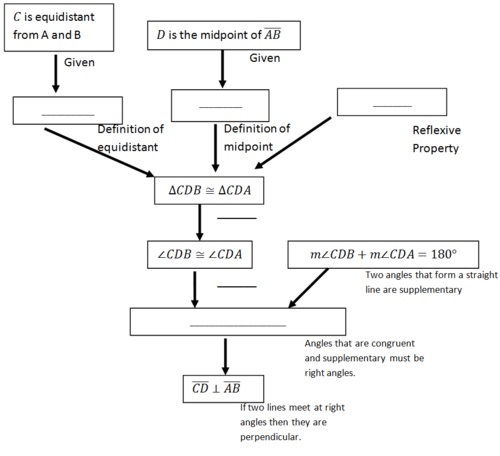
Points on a Perpendicular Bisector
::直垂直双侧区段的点数

播放段落

Prove that points on the perpendicular bisector of a line segment are equidistant from the endpoints of the line segment.
::证明一直线段直径直径对直线段直角两侧的点数与直线段端点的点数相等。

播放段落

Start by exploring this claim. Draw a picture of a line segment and a perpendicular bisector of this segment. Remember that a perpendicular bisector is perpendicular to the line segment (meets it at a right angle) and bisects the line segment (cuts it in half).
::以探索此主张开始 。 请绘制一条线段和此线段的直角双向双向线段的图片 。 请记住, 直角双向区段与线段( 以右角度将其切除) 垂直, 并双切线段( 将线段切除为两半 ) 。

播放段落

The claim is that any point on the perpendicular bisector (such as point $\begin{array}{r}C\end{array}$ ), is the same distance away from each endpoint . In other words, the claim is that for some generic point $\begin{array}{r}C\end{array}$ on the perpendicular bisector, $\begin{array}{r}\overline{AC}\cong \overline{BC}\end{array}$ . 
::这项索赔是,垂直两分区的任何点(如C点)与每一端点的距离相同。换句话说,这项索赔是,对于垂直两分区的某些通用点C,AC BC'。

播放段落

To prove the original statement, it will suffice to prove that if $\begin{array}{r}\stackrel{\leftrightarrow }{CD}\end{array}$ is the perpendicular bisector to $\begin{array}{r}\overline{AB}\end{array}$ with $\begin{array}{r}D\end{array}$ on $\begin{array}{r}\overline{AB}\end{array}$ , then $\begin{array}{r}\overline{AC}\cong \overline{BC}\end{array}$ using the above diagram as a reference. Remember, in general you can use any style of proof that you prefer. Here is a flow diagram. To prove this statement, you will show that the two triangles are congruent and then that the $\begin{array}{r}\overline{AC}\end{array}$ and $\begin{array}{r}\overline{BC}\end{array}$ are corresponding parts so must be congruent.
::为了证明最初的语句,只要证明CD是AB和AB的直角两侧区段,然后AC =BC 以上述图表作为参考。请记住,一般来说,您可以使用您喜欢的任何类型的证据。这里是一个流程图。为了证明这一语句,您可以看到两个三角形是相近的,然后,AC和BC是相应的部分,因此必须是相匹配的。

播放段落

Points on a perpendicular bisector of a line segment are equidistant from the segment's endpoints  is a theorem. Now that it has been proven, you can use it in future proofs without proving it again.
::直线段直角两分线上的点数与断端点的定理相近。 现在,它已被证实, 您可以在未来的证明中使用它, 而不再次证明它 。

---

播放段落

Examples
::实例实例实例实例

播放段落

Example 1
::例1

播放段落

Consider line $\begin{array}{r}l\end{array}$ and a point $\begin{array}{r}P\end{array}$ that is not on line $\begin{array}{r}l\end{array}$ . How many lines exist that are parallel to $\begin{array}{r}l\end{array}$ and pass through point $\begin{array}{r}P\end{array}$ ?
::考虑一行和一分P,后者不在一线。有多少行与一线平行,通过P点?

播放段落

We know that infinite number of lines can pass through a given point. Thus, infinite lines can pass through point $\begin{array}{r}P\end{array}$ . But, not all the lines are parallel to line $\begin{array}{r}l\end{array}$ . A s stated by the famous Scottish mathematician John Playfair in Playfair's axiom, there is only one line passing through $\begin{array}{r}P\end{array}$ which will be parallel to line $\begin{array}{r}l\end{array}$  (i.e. line $\begin{array}{r}m\end{array}$ ). This is also known as the parallel postulate.
::我们知道,无限的线条可以通过一个特定点。因此,无限的线条可以通过P点。但是,并非所有的线条都与l线线平行。正如著名的苏格兰数学家约翰·普菲尔法尔在Playfair的方言中所说,只有一条线可以通过P线,与l线线(即线M)平行。这也被称为平行的假设。

播放段落

Example 2
::例2

播放段落

If corresponding angles are congruent, then are lines that form them parallel to each other?
::如果相应的角度一致, 那么形成这些角度的线条是平行的吗 ?

播放段落

This is known as the converse of the corresponding angles postulate. The original postulate said:
::这被称为对应角度假设的对立面。 最初假设说:

播放段落

Original : If lines are parallel, then corresponding angles are congruent.
::原始: 如果线条是平行的, 那么相应的角度是一致的 。

播放段落

Here, the "if" part of the statement (known as the hypothesis) is switched with the "then" part of the statement (known as the conclusion).
::在这里,声明的“如果”部分(称为假设)与声明的“当时”部分(称为结论)调换。

播放段落

Converse : If corresponding angles are congruent, then lines are parallel.
::反向: 如果对应角度一致, 那么线条是平行的 。

播放段落

In general, just because a statement is true doesn't necessarily mean its converse is true. In this case, the converse does happen to be true. The only way for corresponding angles to be congruent is for the lines to be parallel. The corresponding angles converse is also a postulate, which means it is accepted as true without proof.
::一般来说,仅仅因为声明是真实的,并不必然意味着其反义是真实的。 在这种情况下,反义是真实的。 对应角度一致的唯一办法是线条平行。 对应角度的反义也是假设,这意味着在没有证据的情况下被接受为真实。

播放段落

Example 3
::例3

播放段落

Prove that if lines are parallel, then (such as $\begin{array}{r}\mathrm{\angle }3\end{array}$ and $\begin{array}{r}\mathrm{\angle }6\end{array}$ ) are supplementary.
::证明如果线条是平行的,那么(例如3和6)是补充性的。

播放段落

In general you can use any style of proof that you prefer. Here, use a paragraph proof.
::一般而言,您可以使用您喜欢的任何类型的证明。这里,请使用段落证明。

播放段落

$\begin{array}{r}\mathrm{\angle }3\cong \mathrm{\angle }5\end{array}$ because they are alternate interior angles created by parallel lines and alternate interior angles are congruent when lines are parallel. $\begin{array}{r}m\mathrm{\angle }3=m\mathrm{\angle }5\end{array}$ because congruent angles have the same measure. $\begin{array}{r}m\mathrm{\angle }5+m\mathrm{\angle }6={180}^{\circ }\end{array}$ because two angles that form a line are supplementary. By substitution , $\begin{array}{r}m\mathrm{\angle }3+m\mathrm{\angle }6={180}^{\circ }\end{array}$ . $\begin{array}{r}\mathrm{\angle }3\end{array}$ and $\begin{array}{r}\mathrm{\angle }6\end{array}$ are supplementary because two angles with measures that add to $\begin{array}{r}{180}^{\circ }\end{array}$ are supplementary.
::35 因为它们是平行线条创造的另外的内部角, 当线条平行时, 其它内部角是相近的。 m3=m5 因为相容角具有相同的度量。 m5+m6=180 = @因为组成线条的两个角度是补充的。 替换为 m3+m6=180 。 3和6是补充的, 因为两个角度加上了180的补充措施 。

播放段落

If two parallel lines are cut by a transversal, then same side interior angles are supplementary  is a theorem . Now that it has been proven, you can use it in future proofs without proving it again.
::如果两条平行线被横切切开,那么同一侧内侧角度作为补充就是一个定理。既然它已经得到证实,你就可以在今后的证据中使用它,而不必再次证明它。

播放段落

Example 4
::例4

播放段落

Prove that if alternate interior angles are congruent, then the lines that form them are parallel.
::证明如果其它内部角度是相似的,则构成这些角度的线条是平行的。

播放段落

This is the converse of the alternate interior angles theorem.
::这是替代内部角度定理的反方向 。

播放段落

Original: If lines are parallel, then alternate interior angles are congruent.
::原始: 如果线条平行, 那么其他内部角度是相似的 。

播放段落

Here, the "if" part of the statement (known as the hypothesis) is switched with the "then" part of the statement (known as the conclusion).
::在这里,声明的“如果”部分(称为假设)与声明的“当时”部分(称为结论)调换。

播放段落

Converse: If alternate interior angles are congruent, then lines are parallel.
::反向 : 如果其它内部角度一致, 那么线条是平行的 。

播放段落

To prove this statement, start with a picture of alternate interior angles that are assumed to be congruent, but don't assume the lines are parallel. In the picture below, assume $\begin{array}{r}\mathrm{\angle }1\cong \mathrm{\angle }2\end{array}$ . Prove that $\begin{array}{r}m\Vert n\end{array}$ (two parallel bars indicate parallel lines).
::要证明此语句, 请先从假设相似的替代内部角度开始, 但不要假设线条是平行的 。 在下面的图片中, 请假设 m {1\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\

播放段落 Statements ::声明声明 声明 声明 声明 声明 声明 声明 声明 声明 声明 声明 声明 声明 声明 声明 声明 声明 声明 声明 声明	播放段落 Reasons ::原因原因原因原因
$\begin{array}{r}\mathrm{\angle }1\cong \mathrm{\angle }2\end{array}$	播放段落 Given ::给
$\begin{array}{r}\mathrm{\angle }1\cong \mathrm{\angle }3\end{array}$	播放段落 Vertical angles are congruent ::垂直角度是相似的
$\begin{array}{r}\mathrm{\angle }2\cong \mathrm{\angle }3\end{array}$	播放段落 Transitive property of congruence ::具有一致性的过境财产
$\begin{array}{r}m\Vert n\end{array}$	播放段落 If corresponding angles are congruent then lines are parallel. ::如果相应的角度一致,则线条平行。

Summary

播放段落 Corresponding angles are called that because their locations correspond: they are formed on different lines but in the same position. ::相应的角度被称作, 因为它们的位置相对应: 它们由不同的线条组成, 但位置相同 。 播放段落 Same side interior angles (sometimes called consecutive interior angles) are on the interior of the figure (between the parallel lines) and on the same side of the transversal.  ::同侧内角(有时称为连续内角)位于图的内部(平行线之间)和横向的同一侧。 播放段落 Alternate interior angles are also on the interior of the figure, but on opposite sides of the transversal.  ::其他内部角度也位于图的内侧,但位于横面的对面。 播放段落 For same side exterior angles (sometimes consecutive exterior angles), if lines are parallel, then same side exterior angles are supplementary.  ::对于相同的侧外部角度(有时是连续的外部角度),如果线条平行,则相同的侧外部角度是补充的。 播放段落 Vertical angles are a pair of opposite angles created by intersecting lines. Vertical angles are congruent. ::垂直角度是横交线产生的一对相反角度。垂直角度是相同的。

---

播放段落

Review
::审查审查审查审查

播放段落

1. Go back up to the section "Vertical Angles are Congruent" where it was proven with a two-column proof. Rewrite this proof in a paragraph format.
::1. 返回到“Vertical angles are Congruent”部分, 该部分用两栏证明证明。 用段落格式重写此证明 。

播放段落

2. Go back up to the section "Alternate Interior Angles are Equal" where it was proven with a paragraph proof. Rewrite this proof with a flow diagram.
::2. 回到“替代的内地角相等”部分,该部分用段落证据加以证明,用流程图重写该证据。

播放段落

3. Go back up to the section "Points on a Perpendicular Bisector" where it was proven with a flow diagram that points on a perpendicular bisector of a line segment are equidistant from the segment's endpoints. Rewrite this proof in a two-column format.
::3. 回到“直角双线段的点”一节,该节用一个流程图证明,该流程图显示,线段直角两侧段的点与该段端点相距相等。用两栏格式重写此证明。

播放段落

4. Go back up to  Example 3 where  the theorem "if lines are parallel then same side interior angles are supplementary" was proved with a paragraph proof. Rewrite this proof in a two-column format.
::4. 回到例3,其中的理论“如果线条平行,而同一侧内角是补充的”,用一段证据证明,用两栏格式重写这一证据。

播放段落

5. Go back up to Example 4 where  the theorem "if alternate interior angles are congruent then lines are parallel" was proved with a two-column proof. Rewrite this proof with a flow diagram.
::5. 回到例4,其中的理论“如果其他内部角度是相同的,那么线线是平行的”,用两栏证明证明了这一点。用流程图重写此证据。

播放段落

6. Alternate exterior angles are outside a pair of lines and on opposite sides of a transversal. $\begin{array}{r}\mathrm{\angle }2\end{array}$ and $\begin{array}{r}\mathrm{\angle }8\end{array}$ are an example of alternate exterior angles. $\begin{array}{r}\mathrm{\angle }1\end{array}$ and $\begin{array}{r}\mathrm{\angle }7\end{array}$ are another example of alternate exterior angles.
::6. 其他外部角度在一对线外,在横向两侧。 2和8是替代外部角度的例子。 1和7是另一个替代外部角度的例子。

播放段落

The theorem "if lines are parallel then alternate exterior angles are congruent" is partially proved below. Fill in the blanks to complete the proof. Note , the angles referenced are from the above picture.
::理论“ 如果线条是平行的, 那么不同的外部角度是相似的” 在下面部分证明。 填空以填满证明 。 注意, 引用的角度来自以上图片 。

播放段落 Statements ::声明声明 声明 声明 声明 声明 声明 声明 声明 声明 声明 声明 声明 声明 声明 声明 声明 声明 声明 声明 声明	播放段落 Reasons ::原因原因原因原因
播放段落 Two parallel lines are cut by a transversal ::两条平行线由横线截断	_________
$\begin{array}{r}\mathrm{\angle }2\cong \mathrm{\angle }6\end{array}$	_________
$\begin{array}{r}\mathrm{\angle }6\cong \end{array}$ _________	播放段落 Vertical angles are congruent. ::垂直角度是相同的 。
_________	播放段落 Transitive property. ::10. 过境财产。

播放段落

7. What is the converse of the theorem "if lines are parallel, then same side interior angles are supplementary"?
::7. " 如果线条是平行的,那么同一侧内侧角度是补充的 " 理论的反义词是什么呢?

播放段落

8. Prove the converse that you wrote in #7. Use any style of proof you prefer.
::8. 证明你在第七版中所写的反义词。 使用任何你喜欢的证明方式。

播放段落

9. Go back up to the Line and Angle Theorems section above where the theorem "points on a perpendicular bisector of a line segment are equidistant from the segment's endpoints" was proved. This theorem could be rewritten as "if a point is on the perpendicular bisector of a line segment, then the point is equidistant from the endpoints of the line segment". What is the converse of this theorem? To check your answer, look at #10.
::9. 回到上面的线和角定理部分,其中“线段端点与线段端点相近”的理论得到了证明,该理论可以被改写为“如果线段端点位于线段端点对面线和角定理,那么点与线段端点相近”。这个理论的反面是什么?要检查你的回答,请看#10。

播放段落

10. The converse of the theorem in #9 is "if a point is equidistant from the endpoints of a line segment, then the point is on the perpendicular bisector of the line segment". To prove this new theorem you can use the picture below.
::10. 第9号定理的反义是“如果一个点与线段端点的等距相等,那么该点与线段端点的直径对等,那么该点则与线段端点的直径对角对齐。” 为了证明这个新的定理, 您可以使用下面的图象 。

播放段落

Assume point $\begin{array}{r}C\end{array}$ is a random point that is equidistant from endpoints $\begin{array}{r}A\end{array}$ and $\begin{array}{r}B\end{array}$ . Point $\begin{array}{r}D\end{array}$ is the midpoint of line segment $\begin{array}{r}\overline{AB}\end{array}$ . Your goal is to show that $\begin{array}{r}\overline{CD}\end{array}$ must be perpendicular to $\begin{array}{r}\overline{AB}\end{array}$ $\begin{array}{r}(\overline{CD}\perp \overline{AB})\end{array}$ . This new theorem is partially proved below. Fill in the blanks to complete the proof.
::假设点C是一个随机点,与终点A和B相近。 点D是线段 AB 的中点。 您的目标是显示 CD 必须与 AB (CD AB) 相连接。 新的定理在下面部分得到验证。 填空以填满证据 。

播放段落

In 11-13, you will prove that if two angles are complementary to the same angle, then the two angles are congruent.
::11-13时,你会证明 如果两个角度是同一个角度的补充, 那么这两个角度是相同的。

播放段落

11. Draw a generic picture of this situation and label the three angles.
::11. 绘制关于这种情况的通用图象,并标出三个角度。

播放段落

12. What are the "givens" from your picture? What are you trying to prove?
::12,你的照片里有什么"礼物" 你想证明什么?

播放段落

13. Write a proof of the statement using whatever proof style you prefer.
::13. 使用任何你喜欢的证明风格,为说明书写一份证明。

播放段落

14. Using your work from 11-13 to help, prove that if two angles are supplementary to the same angle, then the two angles are congruent.
::14. 利用11-13年的工作提供帮助,证明如果两个角度是同一角度的补充,那么这两个角度是相同的。

播放段落

15. Give at least 3 methods for proving that lines are parallel.
::15. 提供至少三个方法来证明线条是平行的。

播放段落

16. Given: $\begin{array}{r}\mathrm{\angle }B\end{array}$ is supplementary with $\begin{array}{r}\mathrm{\angle }D\end{array}$ and $\begin{array}{r}\mathrm{\angle }F\end{array}$ is supplementary with $\begin{array}{r}\mathrm{\angle }D\end{array}$ .
::16. 鉴于:B是补充,D是补充,F是补充,D是补充。

播放段落

Prove: $\begin{array}{r}\mathrm{\angle }B\cong \mathrm{\angle }F\end{array}$
::证明:

播放段落

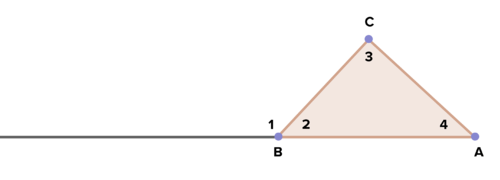
17. Prove that the exterior angle of a triangle is equal to the sum of the two remote interior angles. Use the diagram below to assist you.
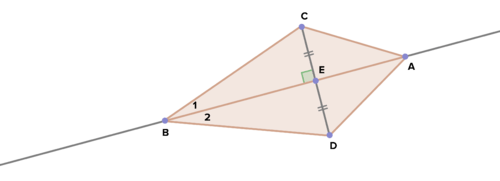
::17. 证明三角形的外角等于两个边远内角的总和,使用下图协助您。

播放段落

18. Given: A and B are on the perpendicular bisector of $\begin{array}{r}\overline{CD}\end{array}$
::18. 鉴于:A和B位于CD的垂直两侧部分上。

播放段落

Prove: ACBD is a kite
::证明:《生物多样性公约》是风筝

播放段落

19. Use the diagram above to prove that $\begin{array}{r}\mathrm{\angle }1\cong \mathrm{\angle }2\end{array}$ . Anything proven in the last proof can also be used here without re-writing.
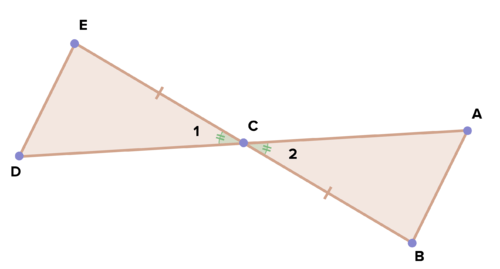
::19. 使用上面的图表来证明%1 @%2。 任何在最后证据中证明的证据都可以在这里使用,无需重新写。

播放段落

20. Given: $\begin{array}{r}\mathrm{\angle }1\cong \mathrm{\angle }2\end{array}$ ; $\begin{array}{r}\overline{EC}\cong \overline{CB}\end{array}$ ; point C is the midpoint of $\begin{array}{r}\overline{DA}\end{array}$
::20. 参照:%12;EC CB;中点C是DA的中点。

播放段落

Prove: $\begin{array}{r}\mathrm{\angle }D\cong \mathrm{\angle }A\end{array}$ .
::证明:

播放段落

Review (Answers) 
::审查(答复)

播放段落

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。