三角交汇的理论论

播放段落

The Center of a Triangle
::三角中心

播放段落

A triangle is a fascinating shape in a number of ways. One is that only have a single center .
::三角形在许多方面是一个迷人的形状。一个是只有一个中心。

播放段落

The centroid , incenter , circumcenter , and orthocenter are four common centers of triangles, and each is identified in a different way.
::中间体、中间体、中间体和正心体是三角形的四个共同中心,每个中心以不同的方式被识别。

播放段落

The Centroid
::中 中心

播放段落

The median of a triangle is a line segment that connects the midpoint of one side of the triangle with the opposite vertex .
::三角形的中位数是一条线段,将三角形一边的中点与相反的顶点连接起来。

播放段落

Something interesting happens when you consider the three medians of a triangle.
::当你考虑三角形的三中位数时 会发生一些有趣的事

播放段落

Click the small blue arrow next to the image below and then drag the orange vertices to reshape the triangle. You will see that no matter what shape the triangle, all three always intersect at a single point . This point is called the centroid of the triangle.
::单击下方图像旁边的小蓝箭头,然后拖动橙色的顶部来重塑三角形。不管三角形的形状如何,你都会看到,所有三角形总是在一个点上交叉。这个点被称为三角形的中圆形。

播放段落

The Orthocenter
::东正教

播放段落

The of a triangle is a line that is perpendicular to one side of the triangle and passes through the opposite vertex. The altitude is always a height of the triangle, and, interestingly, sometimes  occurs outside the triangle entirely.
::三角形是一个直线,直通三角形的一面,穿过相反的顶点。高度总是三角形的高度,有趣的是,有时在三角形外完全出现。

C onsider what happens when the three altitudes of a triangle intersect. 播放段落

Click the small blue arrow next to the image below and then drag the orange vertices to reshape the triangle. It turns out that all three altitudes always intersect at the same point - called orthocenter of the triangle.
::单击下方图像旁边的蓝色小箭头,然后拖动橙色的顶部来重塑三角形。结果发现所有三个高度总是在同一点 -- -- 称为三角形的正弦角 -- -- 交叉。

 

 

播放段落

The Circumcenter 
::中环

播放段落

Recall that a perpendicular bisector of a segment is a line that bisects the segment and meets the segment at a right angle .
::回顾一个段的垂直两分形是一条线,将段分成两部分,以正确角度与段相匹配。

播放段落

As you might have guessed by now, t he perpendicular bisectors of each segment of a triangle all intersect also.
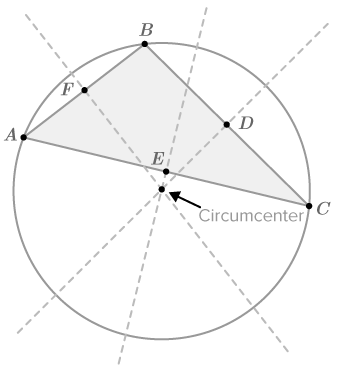
::正如你现在所猜想的 三角形中每个部位的垂直两分形 也都相互交叉

播放段落

Click the small blue arrow next to the image below and then drag the orange vertices to reshape the triangle. You will see that no matter what shape the triangle, all three always intersect at a single point. This point is called the circumcenter of the triangle.
::单击下方图像旁边的小蓝箭头,然后拖动橙色的顶部来重塑三角形。不管三角形的形状如何,你都会看到,所有三角形总是在一个点上交叉。这个点被称为三角形的环点。

播放段落

The circumcenter is also the center of the triangle's circumcircle - the circle that passes through all three of the triangle's vertices,  which is the smallest circle that will entirely contain the triangle.
::圆环点也是三角圆环圈的中心—— 穿过三角形所有三个顶端的圆圈, 这是将完全包含三角形的最小的圆圈。

播放段落

The Incenter
::开 开 开

播放段落

Also recall that an angle bisector of an angle is a line that bisects the angle. This means that the line divides the angle into two congruent angles.
::还提醒大家注意,角的一个角分区是角的两分线,这意味着线将角分为两个相同的角。

播放段落

T he angle bisectors of each angle of a triangle meet at the last of the four centers in this lesson.
::三角形角每个角的角角对角 是在这堂课中四个中心中最后一个相会的角角对角。

播放段落

Click the small blue arrow next to the image below and then drag the orange vertices to reshape the triangle. It turns out that all three angle bisectors always intersect at the same point - called incenter of the triangle.
::单击下方图像旁边的蓝色小箭头,然后拖动橙色的顶部来重塑三角形。结果发现,所有三个角度的双角区段总是在同一点交叉 -- -- 称为三角形的中间点。

播放段落

The incenter  is the center of the triangle's incircle - the largest circle that fits entirely inside the triangle.
::中枢是三角形圆圈的中心 最大的圆圈 完全适合三角形内部

---

播放段落

Points of Concurrency
::货币计算点

播放段落

Given three randomly located points, it is unlikely that the same line will pass through all three points. If three points do lie on the same line, they are called collinear .
::考虑到三个随机定位点,同一线线不太可能通过所有三个点。 如果三个点位于同一线上,它们就被称为共线。

播放段落

Similarly, given three random lines, it is unlikely that all three lines will intersect at the same point.
::同样,考虑到三条随机线,所有三条线不可能在同一点交叉。

播放段落

When three or more lines do intersect at a point, the point is called a point of concurrency .
::当三条或三条以上线在一个点发生交叉时,该点被称为同货币点。

播放段落

Incredibly, the three angle bisectors, , and altitudes are concurrent in every triangle.
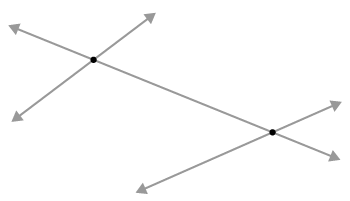
::令人难以置信的是,在每一个三角形中,三个角对角和高度是并行的。

播放段落

Click the small blue arrow next to the image below and then drag the orange point. You will observe that the three lines are concurrent because they all intersect at a single point $\begin{align*}P\end{align*}$ .
::单击下方图像旁边的小蓝箭头,然后拖动橙色点。你会看到这三条线是同时的,因为它们都是在一个P点上交叉的。

 

 

 

---

播放段落

Using Software
::使用软件

播放段落

Use interactive geometry software to construct a triangle and its three perpendicular bisectors. Make a conjecture about the perpendicular bisectors of a triangle.
::使用交互式几何软件构建三角形及其三个直角双向区段。 给三角形的直角双向区段做一个猜测 。

播放段落
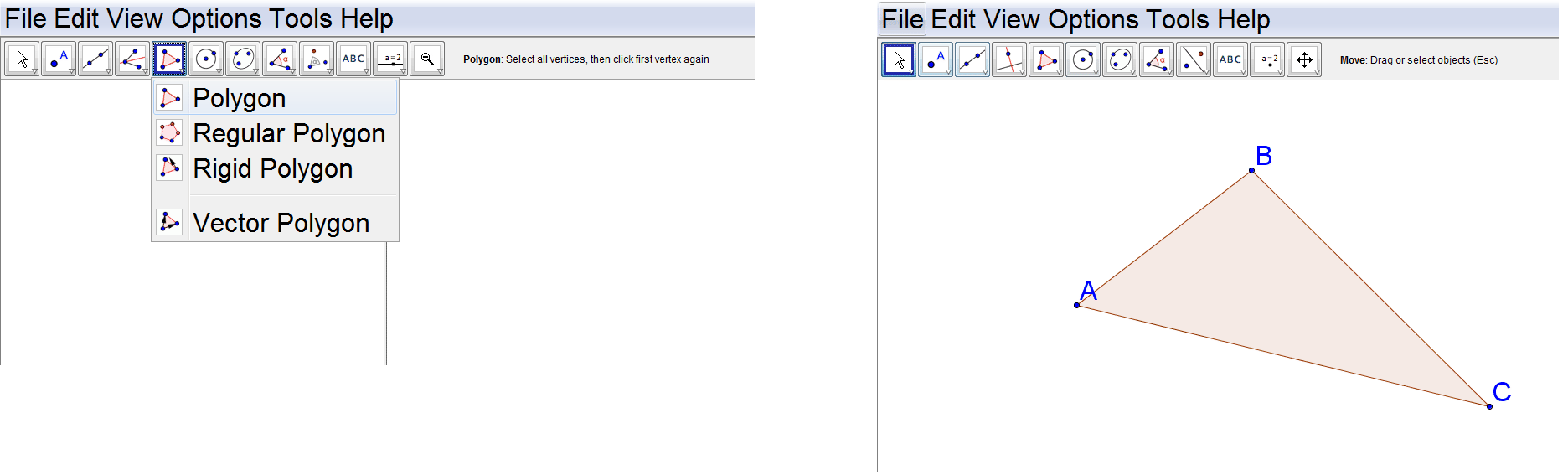
1. Start by constructing a triangle:
   ::以构建三角形开始 :

 

播放段落
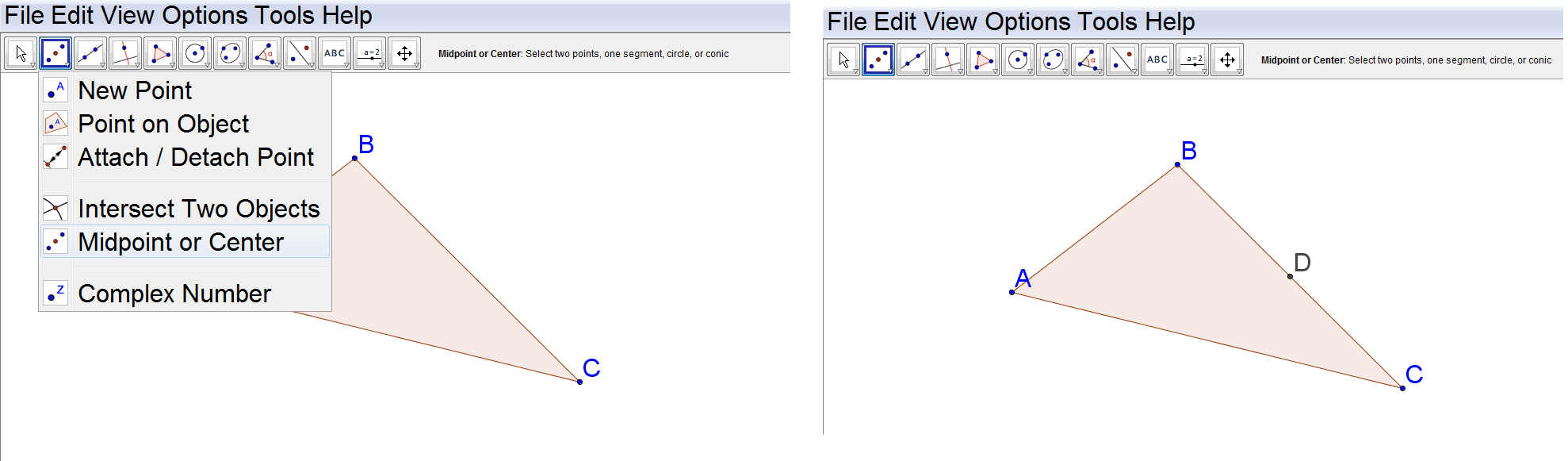
2. Next construct the midpoint of one side of the triangle:
   ::下一步构造三角形一边的中点 :

 

播放段落
3. Next construct a line perpendicular to that side of the triangle that passes through the midpoint:
   ::下一个构造直径于三角形侧的直线, 穿过中点 :

 

播放段落
4. Repeat for the other two sides of the triangle:
   ::重复三角形其他两侧:

 

播放段落

You should notice that the three perpendicular bisectors meet at a point. Also notice that if you move the points that define the triangle, the perpendicular bisectors remain perpendicular bisectors, and they continue to meet at a point. This point of concurrency is called the circumcenter of a triangle.
::您应该注意到, 3个垂直双向区块在一个点上相会 。 同时请注意, 如果您移动了确定三角形的点, 则垂直双向区块仍然是垂直的双向区块, 并且它们会在一个点上继续相会 。 这个货币点被称为三角形的环点 。

播放段落

In the interactive below, you can attempt the construction yourself.
::在下面的互动中,你可以自己尝试建筑。

 

 

---

播放段落

Writing Proofs
::书写证明

播放段落

Prove that the three perpendicular bisectors of any triangle meet at a point.
::证明任何三角形的三个直角两侧区域 在一个点相遇

播放段落

Consider $\begin{align*}\triangle ABC\end{align*}$ with perpendicular bisectors $\begin{align*}m\end{align*}$ , $\begin{align*}n\end{align*}$ and $\begin{align*}l\end{align*}$ .
::考虑使用具有直肠双向分形 m、 n 和 1 的 ABC。

播放段落

Lines $\begin{align*}m\end{align*}$ and $\begin{align*}n\end{align*}$ intersect at a point $\begin{align*}O\end{align*}$ . This point is equidistant from points $\begin{align*}A\end{align*}$ and $\begin{align*}B\end{align*}$ because it is on line $\begin{align*}m\end{align*}$ , the perpendicular bisector of $\begin{align*}\overline{AB}\end{align*}$ . This point is also equidistant from points $\begin{align*}A\end{align*}$ and $\begin{align*}C\end{align*}$ because it is on line $\begin{align*}n\end{align*}$ , the perpendicular bisector of $\begin{align*}\overline{AC}\end{align*}$ . Using substitution, it can be concluded that $\begin{align*}OA = OB = OC\end{align*}$ .
::线 m 线和 n 线在 O 点交叉。 这个点与 A 点和 B 点相距相等, 因为它位于 AB 的 直径线 m 线上。 这个点也与 A 点和 C 点相距相等, 因为它位于 线 n 线上, 是 AC 的 直径 。 使用替代, 可以得出 OA = OB=OC 的结论 。

播放段落

Therefore, the point of intersection is equidistant from $\begin{align*}B\end{align*}$ and $\begin{align*}C\end{align*}$ , and so must lie on line $\begin{align*}l\end{align*}$ , the perpendicular bisector of $\begin{align*}\overline{BC}\end{align*}$ . Line $\begin{align*}l\end{align*}$ intersects lines $\begin{align*}m\end{align*}$ and $\begin{align*}n\end{align*}$ at the same point, so the three perpendicular bisectors meet at one point.
::因此,十字路口的点与B和C相距相当,因此必须位于线I上,即“BC”的直角两侧。线I在同一点交叉线m和n,因此,三个直角两侧的一条线在一个点上汇合。

播放段落

The statement “ the three perpendicular bisectors of any triangle meet at a point ” is a theorem . Now that it has been proven, you can use it in future proofs without proving it again.
::“任何三角形相交点上的三个直角两侧区块”的语句是一个定理。 既然已经证明了这一点,你可以在未来的证据中使用它,而不必再次证明。

---

播放段落

Investigating the Circumcenter of a Triangle
::调查三角圆环中心

播放段落

Use interactive geometry software to investigate the circumcenter of a triangle. In particular, construct a circle with the circumcenter as its center. Can you find any interesting circles?
::使用交互式几何软件来调查三角形的环绕点。 特别是, 构造一个以环绕点为中心的圆圈。 您能找到有趣的圆圈吗 ?

播放段落

If you construct a circle with the circumcenter as its center that passes through vertex $\begin{align*}A\end{align*}$ , you should notice that the circle also passes through vertices $\begin{align*}B\end{align*}$ and $\begin{align*}C\end{align*}$ . Does this seem surprising?
::如果以环中点为中心构造一个圆圈,穿过脊椎A,你应该注意到圆圈也穿过脊椎B和C。这似乎令人吃惊吗?

播放段落

For any triangle, there exists only one circle that passes through all three of its vertices. This circle is said to circumscribe the triangle, and the circumcenter is always the center of this circle.
::对于任何三角形, 只有一个圆圈可以穿过所有三个顶端。 据说这个圆圈可以限定三角形, 圆环始终是这个圆圈的中心 。

---

播放段落

CK-12 PLIX Interactive
::CK-12 PLIX 交互式互动

 

 

---

播放段落

Examples
::实例实例实例实例

播放段落

Example 1
::例1

播放段落

For any triangle, the perpendicular bisectors of the three sides of the triangle meet at one point called the circumcenter. Why is this point called the circumcenter and what does it have to do with circles?
::对于任何三角形来说,三角形三边的直角双翼相交在一个叫做环中点的地方相交。 为什么这个点被称为环中点? 它与圆圈有什么关系?

播放段落

As shown above, the circumcenter is not only the intersection of the three perpendicular bisectors, but it is also the center of the circle that circum scribes the triangle. This is why it is called the circumcenter .
::如上所示,环中值不仅是三个直角两分形的交叉点,而且也是三角圈圈的中间点。这就是它为什么被称为环中值的原因。

播放段落

Example 2
::例2

播放段落

Use interactive geometry software to construct a triangle and its three medians. Move the triangle around and see what happens. Make a conjecture about the medians of a triangle.
::使用交互式几何软件构建三角形及其三个中位数。 移动三角形并观察结果。 对三角形的中位数进行猜测 。

播放段落

Start by constructing a triangle and the midpoints of the three sides. Then, construct line segments connecting each midpoint to the opposite vertex.
::以构建三角形和三边的中点开始。 然后, 构建连接每个中点到相反顶点的线段 。

播放段落

You should notice that the three medians meet at a point, even if you move vertices $\begin{align*}A\end{align*}$ , $\begin{align*}B\end{align*}$ or $\begin{align*}C\end{align*}$ . As the centroid, the point of intersection divides each median in a 2:1 ratio .
$\begin{align*}AG=\frac{2}{3}AD, \end{align*}$ $\begin{align*}BG=\frac{2}{3}BE\end{align*}$ and $\begin{align*}CG=\frac{2}{3}CF\end{align*}$ .
::您应该注意到,即使您移动了甲型、乙型或丙型脊椎,这三种中位数也在一个点相遇。 作为中间体,交叉点将每个中位数分隔为2:1。 AG=23AD、BG=23BE和CG=23CF。

 

 

播放段落

Example 3
::例3

播放段落

Prove that the point of intersection for two medians of a triangle divides each median into two segments in a 2:1 ratio .
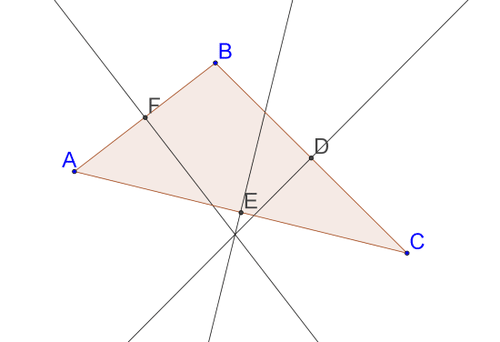
::证明三角形两个中位数的交叉点将每个中位数按2:1的比例分为两个区段。

播放段落

Consider two medians $\begin{align*}(\overline{FC}\end{align*}$ and $\begin{align*}\overline{AD})\end{align*}$ and their point of intersection $\begin{align*}(G)\end{align*}$ , as shown below. Also shown below is point $\begin{align*}H\end{align*}$ , the midpoint of $\begin{align*}\overline{AG}\end{align*}$ and point $\begin{align*}J\end{align*}$ , the midpoint of $\begin{align*}\overline{GC}\end{align*}$ .
::考虑两个中位数('FC'和'AD')及其交叉点(G),如下所示。以下还显示H点,AG的中点和J点,GC的中点。

播放段落

$\begin{align*}\overline{FD}\end{align*}$ is a segment that connects the midpoints of a triangle. This means it is half the length of $\begin{align*}\overline{AC}\end{align*}$ and parallel to $\begin{align*}\overline{AC}\end{align*}$ . Therefore, $\begin{align*}FD=\frac{1}{2}AC\end{align*}$ and $\begin{align*}\overline{FD}\|\overline{AC}\end{align*}$ .
::FD 是一个连接三角形中点的线段。 这意味着它长度为 AC 的一半, 与 AC 平行。 因此, FD = 12AC 和 FD = AC 。

播放段落

Similarly, $\begin{align*}\overline{HJ}\end{align*}$ is a segment that connects the midpoints of a triangle $\begin{align*}(\triangle AGC)\end{align*}$ , so it is also half the length of $\begin{align*}\overline{AC}\end{align*}$ and parallel to $\begin{align*}\overline{AC}\end{align*}$ . Therefore, $\begin{align*}HJ=\frac{1}{2}AC\end{align*}$ and $\begin{align*}\overline{HJ}\|\overline{AC}\end{align*}$ .
::类似地,HJ是一个连接三角形中点的区段, 也相当于AC的长度的一半, 与AC的平行。 因此,HJ=12AC和HJ'AC。

播放段落

By substitution, $\begin{align*}HJ=FD\end{align*}$ and thus $\begin{align*}\overline{HJ}\cong\overline{FD}\end{align*}$ . Also, $\begin{align*}\overline{HJ}\| \overline{FD}\end{align*}$ because both lines are parallel to $\begin{align*}\overline{AC}\end{align*}$ . This means that $\begin{align*}\angle GHJ \cong \angle GDF\end{align*}$ and $\begin{align*}\angle GJH \cong \angle GFD\end{align*}$ because they are , which are congruent when lines are parallel.
::换句话说,HJ=FD,因此是HJ=FD。另外,HJ=FD,因为两条线都与AC平行。这意味着GHJ=GDF和GJH=GFD,因为两条线在线平行时是相同的。

播放段落

Because two pairs of angles and a pair of included sides is congruent, $\begin{align*}\triangle GHJ \cong \triangle GDF\end{align*}$ by $\begin{align*}ASA \cong\end{align*}$ . Therefore, $\begin{align*}\overline{HG}\cong\overline{GD}\end{align*}$ and $\begin{align*}\overline{GJ}\cong \overline{GF}\end{align*}$ because they are corresponding parts of .
::因为两对角度和一对包括的两面是相近的, ASA的GHJGDF。因此,HG&G和GJ'FF是相应的部分。

播放段落

$\begin{align*}H\end{align*}$ is the midpoint of $\begin{align*}\overline{AG}\end{align*}$ , so $\begin{align*}\overline{AH} \cong \overline{HG}\end{align*}$ . This means the ratio of $\begin{align*}AG:GD\end{align*}$ must be 2:1. Similarly, $\begin{align*}J\end{align*}$ is the midpoint of $\begin{align*}\overline{CG}\end{align*}$ , so $\begin{align*}\overline{CJ}\cong\overline{JG}\end{align*}$ . The ratio of $\begin{align*}CG:GF\end{align*}$ must also be 2:1.
::H是AG的中点,所以是AG的中点。这意味着AG的比例:GD必须是2: 1。同样,J是CG的中点,所以CJ是JG。CG:GF的比例也必须是2: 1。

播放段落

Note that the statement “the medians of a triangle intersect at a point that divides each median in a 2:1 ratio ” is a theorem.
::请注意,“三角交错点中位数,以2:1的比例将中位数除以”是一个定理。

播放段落

Example 4
::例4

播放段落

W hy do the three medians of any triangle meet at a point?
::为什么任何三角形的三个中位数会在一个点相遇?

播放段落

By investigation, you can see that the point of intersection of any two medians is in a 2:1 ratio such that the segment from the vertex to the point of intersection is the longer segment.
::通过调查,你可以看到任何两个中位数的交叉点在2:1的比例中,从顶端到交叉点的段段是较长的段。

播放段落

Now, consider a triangle with two medians, $\begin{align*}m\end{align*}$ and $\begin{align*}n\end{align*}$ , constructed. Those medians meet at a point $\begin{align*}P\end{align*}$ that divides each median in a 2:1 ratio .
::现在, 请考虑一个三角形, 以两个中位数 m 和 n 构造。 这些中位数在 P 点会合, 以 2:1 的比例将每个中位数分隔开来 。

播放段落

Consider the same triangle with medians $\begin{align*}m\end{align*}$ and $\begin{align*}l\end{align*}$ constructed. Those medians must also meet at a point $\begin{align*}P^\prime\end{align*}$ that divides each median in a 2:1 ratio . 
::以 m 和 l 中位数来考虑相同的三角形。 这些中位数也必须在P 点达到, 将中位数除以 2: 1 的比例 。

播放段落

$\begin{align*}P\end{align*}$ must be the same as $\begin{align*}P^\prime\end{align*}$ , because both points divide median $\begin{align*}m\end{align*}$ in the same 2:1 ratio. Therefore, all three medians must meet at the same point $\begin{align*}P\end{align*}$ .
::P必须和P’相同,因为两个点的中位数Mm以2:1的比例差。 因此,所有三个中位数都必须在同一点达到P。

播放段落

Note that the statement “ the three medians of a triangle intersect at a point ” is a theorem.
::请注意,“三角形在一个点上交叉的三中位数”是一个定理。

Summary

播放段落 The median of a triangle is a line segment that connects the midpoint of one side of the triangle with the opposite vertex. ::三角形的中位数是一条线段,将三角形一边的中点与相反的顶点连接起来。 播放段落 The incenter is the point where the three angle bisectors of a triangle intersect. ::中间点是三角形的三个角对角相交点。 播放段落 The centroid is the point of intersection of the medians in a triangle. ::中间体是三角形中中位点的交叉点。 播放段落 The circumcenter is the point of intersection of the perpendicular bisectors of the sides in a triangle. ::中间点是三角形两侧垂直两侧的交叉点。 播放段落 An altitude of a triangle is a line segment from a vertex and is perpendicular to the opposite side. It is also called the height of a triangle. ::三角形的高度是脊椎的直线段,垂直到对面。它也称为三角形的高度。 播放段落 Orthocenter : The point of concurrency for the altitudes of triangle. ::Orthocenter: 三角形高度的货币计算点 。

---

---

播放段落

Review
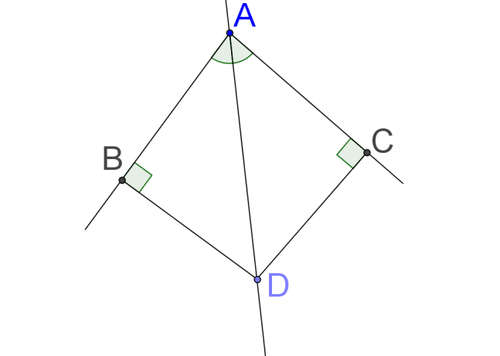
::审查审查审查审查

播放段落

1. Using a two column proof prove the theorem “ any point on the angle bisector of an angle is equidistant from the two rays that define the angle ”, by proving that $\begin{align*}\overline{BD}\cong\overline{DC}\end{align*}$ in the diagram below, where $\begin{align*}\overline{AD}\end{align*}$ is the angle bisector of $\begin{align*}\angle A\end{align*}$ .
::1. 使用两列证明来证明 " 一个角角角的角角两部分的任何点与确定角的两个射线的相等距离 " 的理论,证明在下图中“BD”DC, 其中“A”的角是“A”的角两部分。

播放段落

2. Use interactive geometry software to construct a triangle and its three angle bisectors. Move the triangle around and see what happens. Make a conjecture about the angle bisectors of a triangle.
::2. 使用交互式几何软件构建三角形及其三个角对角区段。移动三角形,看看会发生什么。对三角形角对角对角对角进行推测。

播放段落

3. Use a paragraph proof to prove that the three angle bisectors of any triangle meet at a point.
::3. 使用段落证据证明任何三角形的三个角对角分区在一个点相遇。

播放段落

4. The three angle bisectors of a triangle meet at a point called the incenter. Use geometry software to investigate the incenter. In particular, construct a circle with the incenter as its center. Can you find any interesting circles?
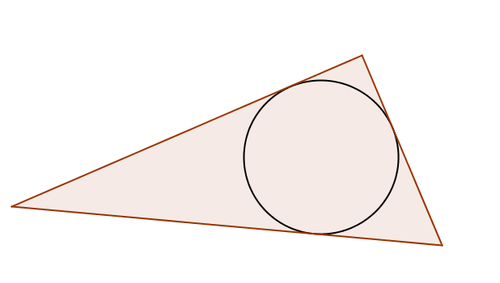
::4. 三角形的三个角对角相交点在一个称为中间点的地方相交,使用几何软件来调查中间点,特别是以中间点为中心建立一个圆圈,你能找到任何有趣的圆圈吗?

播放段落

5. The circle below is inscribed in the triangle. The center of the circle is the incenter of the triangle. Why do you think the incenter is called the incenter?
::5. 下面的圆以三角形标出。圆的中心是三角形的中心。你为什么认为中间点被称为中间点?

播放段落

6. Use interactive geometry software to construct a triangle and its three altitudes. Move the triangle around and see what happens. Make a conjecture about the altitudes of a triangle.
::6. 使用交互式几何软件构建三角形及其三个高度。移动三角形,看看会发生什么。对三角形的高度进行推测。

播放段落

7. The three altitudes of a triangle always meet at a point called the orthocenter. Where is the orthocenter located for right triangles?
::7. 三角形的三高度总是在直角点相交,右三角形的正方位在哪里?

播放段落

8. Where is the orthocenter of a triangle located for acute triangles?
::8. 急性三角形三角形的正弦中枢位置在哪里?

播放段落

9. Where is the orthocenter of a triangle located for obtuse triangles?
::9. 斜三角形三角形的正弦中枢位置在哪里?

播放段落

10. Use interactive geometry software to construct a triangle and its circumcenter, centroid, and orthocenter. Hint: It can help to hide lines when you do not need them anymore and/or label the points as you construct them . Move the triangle around and see what happens. Make a conjecture about the relationship between these three points.
::10. 使用交互式几何软件来构造三角形及其周围中心、中子和正弦。 提示 : 它可以帮助隐藏不再需要的线条和/ 或者在构造时标出点。 移动三角形并观察结果。 假设这三点之间的关系 。

播放段落

11. The circumcenter, centroid, and orthocenter are always collinear, creating a line segment called the Euler segment. Are the three points always in the same order on the Euler segment? Make a conjecture.
::11. 环中、中子和正正弦中枢始终是圆形的,形成一个称为欧勒段的线段,这三点是否始终在欧勒段的顺序相同?作出一个猜测。

播放段落

Continue with your triangle from #10 and #11.
::从 # 10 和 # 11 继续您的三角形 。

播放段落

12. Construct the midpoints of the three sides of a triangle.
::12. 构造三角形三边的中点。

播放段落

13. Construct a segment from each vertex to the orthocenter.
::13. 构造从每个顶部到正方形的一段段。

播放段落

14. Construct the midpoints of the three previous segments (the segments connecting the vertices to the orthocenter).
::14. 构造前三个区段的中点( 将顶部与正方形连接的区段) 。

播放段落

15. Construct the midpoint of the Euler segment.
::15. 构造欧勒段的中点。

播放段落

16. Construct a circle centered at the midpoint of the Euler segment that passes through one of the midpoints of the triangle. What do you notice about this circle?
::16. 构建一个以欧勒段中点为中心、穿过三角形中点之一的圆。您注意到关于此圆什么?

播放段落

17. Construct a triangle and its Euler line as previously completed. Now construct a medial triangle, that is, a triangle connecting the midpoints of the sides of the initial triangle. Then construct the Euler line for the medial triangle. Make observations about the relationship between the new Euler line and the original, as well as comparing the circumcenter, centroid, and orthocenter to those of the original.
::17. 构造一个三角形及其先前完成的 Euler 线。 现在构造一个介质三角形, 即连接初始三角形两边中点的三角形。 然后为介质三角形构造 Euler 线。 观察新的 Euler 线和原始线之间的关系, 并将环中线、 中子线和正弦中枢与原始三角形相比较 。

播放段落

Review (Answers)
::审查(答复)

播放段落

To see the answer key for this book, go to the and click on the Answer Key under the ' ' option.
::要查看本书的答案键, 请在“ ” 选项下点击答案键 。