相似性的定义

播放段落
• A similarity transformation results in an image that is the same shape as the pre-image, but may not be the same size - in other words, the image is similar to the pre-image.
  ::相似性转变导致图像的形状与预视前的形状相同,但尺寸可能不同,换言之,图像与预视前的形状相似。

播放段落
• Two figures are similar if a similarity transformation will carry the first figure to the second figure.
  ::如果相似性转换将第一个数字与第二个数字相提并论,则两个数字相似。

播放段落

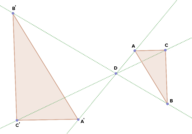
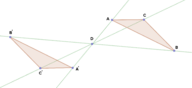
In the picture below, trapezoid $\begin{align*}ABCD\end{align*}$ has been reflected , then rotated , and then dilated with a scale factor of 2 . The first three are all congruent . The final trapezoid is similar to each of the first three trapezoids.
::在下面的图片中, 鼠标ABCD 被反射, 然后旋转, 然后放大为 2 的比例系数 。 前三个是相同的 。 最后一个 类与前三个 类相似 。

播放段落

In the trapezoids above, notice that $\begin{align*}\angle B \cong \angle B^{\prime \prime \prime}\end{align*}$  Also notice that $\begin{align*}B^{\prime \prime \prime} C^{\prime \prime \prime}=2BC\end{align*}$
::注意上面的捕捉类动物 注意BBB 注意BC2BC

播放段落
• In general, similarity transformations preserve angles .
  ::一般而言,相似性转换保留了角度。
播放段落
• Side lengths are enlarged or reduced according to the scale factor of the dilation.
  ::边长根据膨胀的比重系数扩大或缩小。
播放段落
• S imilar figures will have that are the same measure and corresponding sides that are proportional.
  ::类似数字将具有与比例相同的计量和对应边。

播放段落

In order to determine if two shapes are similar, you can:
::为了确定两种形状是否相似,您可以:

播放段落
1. Carefully describe the sequence of similarity transformations necessary to carry the first figure to the second.
   ::仔细描述将第一个数字移到第二个数字所需的相似性变化的顺序。

播放段落

AND/OR
::和/或

播放段落
2. Verify that all corresponding pairs of angles are congruent and all corresponding pairs of sides are proportional.
   ::校验所有相应的角度对齐, 所有对应的两边均成正比 。

---

播放段落

Determining Similarity
::确定相似性

播放段落

Consider the two given $\begin{align*}ABCD\end{align*}$  and $\begin{align*}EFGH.\end{align*}$  To determine whether the two rectangles are similar or not, you see if a similarity transformation would carry rectangle $\begin{align*}ABCD\end{align*}$ to rectangle $\begin{align*}EFGH\end{align*}$ . First rotate rectangle $\begin{align*}ABCD\end{align*}$ $\begin{align*}90^\circ\end{align*}$ counterclockwise about the origin to create rectangle $\begin{align*}A'B'C'D'.\end{align*}$  Then dilate rectangle $\begin{align*}A^\prime B^\prime C^\prime D^\prime\end{align*}$ about the origin with a scale factor of  $\begin{align*}\tfrac12\end{align*}$  to create rectangle $\begin{align*}EFGH.\end{align*}$
::考虑给定的 ABCD 和 EFGH。 要确定这两个矩形是否相似, 您可以看到相似的变换是否将矩形 ABCD 带入矩形 EFGH 。 首先旋转矩形 ABCD90 / 对应时钟, 以创建矩形 A ' B ' C ' D ' 。 然后放大关于起源的矩形 A ' B ' C ' D ' , 以12 为比例因数, 以创建矩形 EFGH 。

播放段落

A rotation followed by a dilation is a similarity transformation. Therefore, the two rectangles are similar. 
::交替后加放大是相似的转换。 因此, 两个矩形是相似的 。

播放段落

Another way to check if two shapes are similar is to verify that all corresponding angles are congruent and all corresponding sides are proportional. Because both shapes are rectangles, all angle measures are $\begin{align*}90^{\text{o}}\!.\end{align*}$  Therefore, all pairs of corresponding angles are congruent.
::检查两个形状相似性的另一个方法就是验证所有对应角度是相近的,所有对应的边是正比的。由于两个形状都是矩形,所有角度的度量都是90o。因此,所有对应角度的对齐都是相近的。

播放段落

For the sides:
::双方:

播放段落
• $\begin{align*}\frac{AD}{EH}=\frac{4}{2}=2\\ \ \\\end{align*}$
  ::ADEH=42=2
播放段落
• $\begin{align*}\frac{DC}{HG}=\frac{8}{4}=2\\ \ \\\end{align*}$
  ::DCHG=84=2
播放段落
• $\begin{align*}\frac{CB}{GF}=\frac{4}{2}=2\\ \ \\\end{align*}$
  ::CBFF=42=2
播放段落
• $\begin{align*}\frac{BA}{FE}=\frac{8}{4}=2\end{align*}$
  ::BAFE=84=2

播放段落

Because all corresponding side lengths are in the same ratio , they are proportional.
::由于所有相应的副长度都相同,因此是成比例的。

播放段落

All corresponding angles are congruent and all corresponding sides are proportional, so the rectangles are similar.
::所有相应的角度是一致的, 所有对应的边是比例的, 所以矩形是相似的 。

播放段落

The symbol for similarity is $\begin{align*}\sim\end{align*}$ . The statement  $\begin{align*}\triangle ABC \sim \triangle DEF\end{align*}$ means “ triangle $\begin{align*}ABC\end{align*}$ is similar to triangle $\begin{align*}DEF\end{align*}$ .” Just as with , the order of the letters matters. $\begin{align*}A\end{align*}$ corresponds to $\begin{align*}D\end{align*}$ , $\begin{align*}B\end{align*}$ corresponds to $\begin{align*}E\end{align*}$ and $\begin{align*}C\end{align*}$ corresponds to $\begin{align*}F.\end{align*}$
::相似的符号为 。 声明 ABCDEF 意指“ 三边ABC 类似于三角的DEF ” 。 和 一样, 字母的顺序也很重要。 A 对应于 D, B 对应于 E 和 C 对应于 F 。

---

播放段落

Finding the Length of Sides
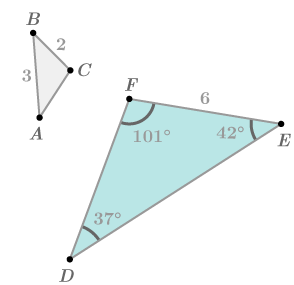
::查找边的长度

播放段落

The two triangles below are similar with $\begin{align*}\triangle ABC \sim \triangle DEF\!.\end{align*}$
::下面的两个三角形与ZABCDEF相似。

播放段落
1. What is $\begin{align*}m \angle A?\end{align*}$
   ::什么是MA?
播放段落
2. What is the length of $\begin{align*}\overline{DE}?\end{align*}$
   ::时间长度是多少?

播放段落

Because the triangles are similar, corresponding angles are congruent and corresponding sides are proportional.
::因为三角形相似, 相应的角度相似, 相应的边是比例的 。

播放段落

$\begin{align*}\therefore \ \angle A = \angle D, \ \angle B = \angle E, \ \angle C = \angle F \ \text{and} \ \ ~ \frac{AB}{DE} = \frac{BC}{EF} = \frac{AC}{DF} \\\end{align*}$
::AD,BE,CF和ABDE=BCEF=ACDF

播放段落

$\begin{align*}\bullet \ \text{Since } \angle A = \angle D, \ m \angle A = m \angle D = 37^\circ \\\end{align*}$
::* 自{AD, mA=mD=37*

播放段落

$\begin{align*} \bullet \frac{BC}{EF} & = \frac{AB}{DE} \\ \ \\ \frac{2}{6} & = \frac{3}{DE} \\ \ \\ DE & = \frac{3 \cdot 6}{2} \\ \ \\ DE & = 9\end{align*}$
::* BCEF=ABDE 26=3DE DE = 362 DE = 9

---

播放段落

CK-12 PLIX Interactive
::CK-12 PLIX 交互式互动

播放段落

Translation Applications in Circle Similarity
::圆圈相似的翻译应用

---

播放段落

Examples
::实例实例实例实例

播放段落

Example 1
::例1

播放段落

What does similarity have to do with transformations?
::相似性与变异有什么关系?

播放段落

Similarity transformations produce . You might think of similar figures as “shapes that are the same shape but different sizes”, but similar figures can always be linked to rigid motions and dilations as well. If two figures are similar, you will always be able to perform a sequence of rigid motions followed by a dilation on one to create the other.
::相似性变换产生 。 您可能会认为类似的数字是“ 形状相同但大小不同的形状 ” , 但类似的数字也总是可以与僵硬的动作和放大法相联系。 如果两个数字相似, 你总是能够进行一系列的僵硬动作, 并随后对一个进行推算以创造另一个。

播放段落

Example 2
::例2

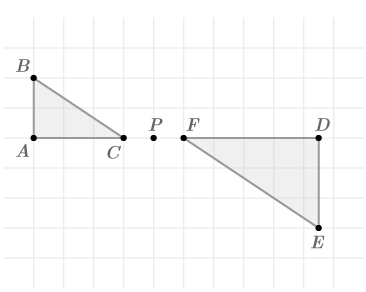
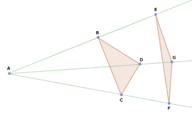
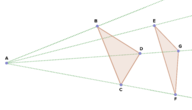
播放段落

Are the two triangles similar? Explain.
::这两个三角形相似吗?

播放段落

Yes, they are similar. Rotate $\begin{align*}\triangle ABC \ 180^\circ\end{align*}$ about point $\begin{align*}P.\end{align*}$  Then, dilate about point $\begin{align*}F\end{align*}$ with a scale factor of 1.5 to create $\begin{align*}\triangle DEF.\end{align*}$
::是的,它们相似。旋转ABC 180约P点。然后,放大F点,使比例系数为1.5,以创建 ZDEF。

播放段落

A rotation followed by a dilation is a similarity transformation. Therefore, the two triangles are similar. 
::旋转后进行放大是相似的转换。 因此, 两个三角形是相似的 。

播放段落

Example 3
::例3

播放段落

Use the triangles from #2 to fill in the blanks.
::使用 # 2 的三角形填充空白 。

播放段落

$\begin{align*}\triangle ABC \sim \underline{\;\;\;\;\;\;\;\;\;\;}\end{align*}$
::* ABC * * ABC * * * ABC * * * ABC * * ABC * * * ABC * * * ABC * * * ABC * * ABC * * ABC * * ABC * * ABC * * * ABC * * * ABC * *

播放段落

$\begin{align*}\angle C \cong \underline{\;\;\;\;\;\;\;\;\;\;}\end{align*}$
::~ C ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~

播放段落

$\begin{align*}\frac{FD}{CA}=\underline{\frac{ED}{}}\end{align*}$
::FDCA=ED_

播放段落

Notice that $\begin{align*}A\end{align*}$ corresponds to $\begin{align*}D,\end{align*}$   $\begin{align*}B\end{align*}$ corresponds to $\begin{align*}E\end{align*}$ , and $\begin{align*}C\end{align*}$ corresponds to $\begin{align*}F.\end{align*}$   This means that $\begin{align*}\triangle ABC \sim \triangle DEF\end{align*}$ .
::通知A对应于D、B对应于E,C对应于F。 这意味着 ABC-DEF。

播放段落

$\begin{align*}\angle C \cong \angle F\end{align*}$ .
::{\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}CáF.

播放段落

$\begin{align*}\frac{FD}{CA}=\frac{ED}{BA}\end{align*}$ because $\begin{align*}\overline{ED}\end{align*}$ and $\begin{align*}\overline{BA}\end{align*}$ are corresponding sides.
::FDCA=EDBA 因为ED和BA是对应方

播放段落

Example 4
::例4

播放段落

Suppose that $\begin{align*}\triangle DOG \sim \triangle CAT\end{align*}$ with $\begin{align*}\frac{AT}{OG}=\frac{1}{3}\end{align*}$ , state what you know about the sides and angles of the two triangles. 
::假设ZADOGCAT与ATOG=13, 说明你对两个三角形的侧面和角度的了解。

播放段落

$\begin{align*}\angle D \cong \angle C\end{align*}$ , $\begin{align*}\angle O \cong \angle A\end{align*}$ , $\begin{align*}\angle G \cong \angle T\end{align*}$ .
::C,OA,GT。

播放段落

$\begin{align*}\frac{CA}{DO} = \frac{AT}{OG} = \frac{CT}{DG}\end{align*}$ .
::CADO=ATOG=CTDG。 (CADO=ATOG=CTDG。 )CADO=ATOG=CTDG。 。 。 。 。

播放段落

Since $\begin{align*}\frac{AT}{OG} = \frac{1}{3}\end{align*}$ $\begin{align*}\therefore \ \triangle DOG\end{align*}$ is a bigger triangle.
::自从ATOG=13 * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * *

播放段落

This means that $\begin{align*}DO=3CA\end{align*}$ , $\begin{align*}OG=3AT\end{align*}$ , and $\begin{align*}DG=3CT\end{align*}$ .
::这意味着DO=3CA、OG=3AT和DG=3CT。

Summary

播放段落 A similarity transformation results in an image that is the same shape as the pre-image, but may not be the same size - in other words, the image is similar to the pre-image. ::相似性转变导致图像的形状与预视前的形状相同,但尺寸可能不同,换言之,图像与预视前的形状相似。 播放段落 A dilation changes the size of a figure, without changing the shape of it. ::膨胀会改变图的大小, 而不改变图的形状 。 播放段落 A ways to check if two shapes are similar:  播放段落 verify that all corresponding angles are congruent and all corresponding sides are proportional.  ::校验所有相应角度的一致性和所有相应边的相称性。 播放段落 describe the sequence of similarity transformations necessary to carry the first figure to the second. ::描述将第一个数字移到第二个数字所需的相似性变化顺序。 ::一种检查两种形状是否相似的方法: 验证所有相应的角度是相近的, 所有对应的侧面是成比例的。 描述将第一个图显示到第二个图所需的相近性变换顺序 。

---

播放段落

Review
::审查审查审查审查

播放段落

1. If two shapes are similar, must they be congruent? Explain.
::1. 如果两种形状相似,它们必须一致吗?

播放段落

2. If two shapes are congruent, must they be similar? Explain.
::2. 如果两种形状是相同的,它们必须相似吗?

播放段落

$\begin{align*}\triangle ABC \sim \triangle DEF\end{align*}$ . Decide if each statement is true or false and explain your answer.
::决定每个声明是真实的还是虚假的 并解释你的答复

播放段落

3. $\begin{align*}\frac{AB}{DE}=\frac{BC}{EF}\end{align*}$
::3. 溴化二苯醚=BCEF

播放段落

4. $\begin{align*}AC \cdot BC=DF \cdot EF\end{align*}$
::4. ACBC=DFEF

播放段落

5. $\begin{align*}\angle B \cong \angle E\end{align*}$
::5. 博爱

播放段落

For #6-#9, are the two triangles similar? If so, give a similarity statement and explain how you know. If not, explain.
::对于#6-9, 两个三角形相似吗? 如果是, 请给出相似声明并解释您是如何知道的。 如果不是, 请解释 。

6.

7.

8.

9.

播放段落

For #10-#12, $\begin{align*}\triangle BAC \sim \triangle DEF\end{align*}$ . Note that the triangles below are not drawn to scale.
::对于 # 10 - # 12, QBACDEF。 请注意, 以下三角不会被拉动为缩放 。

播放段落

10. If $\begin{align*}m \angle A=85^\circ\end{align*}$ and $\begin{align*}m \angle D=50^\circ\end{align*}$ , what is $\begin{align*}m \angle F\end{align*}$ ?
::10. 如果MA=85和MD=50,什么是MF?

播放段落

11. If $\begin{align*}AB=5\end{align*}$ , $\begin{align*}ED=2\end{align*}$ , and $\begin{align*}FD=3\end{align*}$ , what is $\begin{align*}CB\end{align*}$ ?
::11. 如果AB=5, ED=2, FD=3, CB是什么?

播放段落

12. If $\begin{align*}AC=3\end{align*}$ , $\begin{align*}DE=1\end{align*}$ , and $\begin{align*}AC \cong AB\end{align*}$ , what is $\begin{align*}EF\end{align*}$ ?
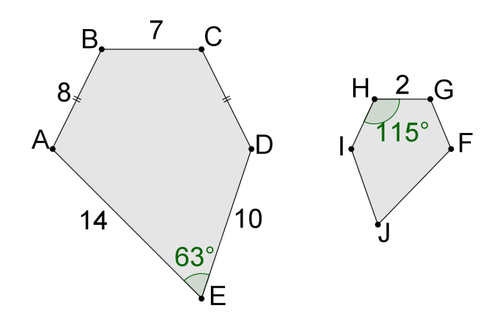
::12. 如果AC=3、DE=1和ACAB, 什么是EF?

播放段落

For #13-#16, $\begin{align*}ABCDE \sim FGHIJ\end{align*}$ . Note that the pentagons below are not drawn to scale.
::对于 #13-#16, ABCDEQFGHIJ。 注意以下的五边没有被拉动到比例 。

播放段落

13. $\begin{align*}GF=?\end{align*}$
::13. GF=?

播放段落

14. $\begin{align*}JF=?\end{align*}$
::14个JF?

播放段落

15. $\begin{align*}JI=?\end{align*}$
::15. 联合执行=?

播放段落

16. $\begin{align*}m \angle J=?\end{align*}$
::16岁?

播放段落

17. Explain two ways to determine whether or not two triangles are similar.
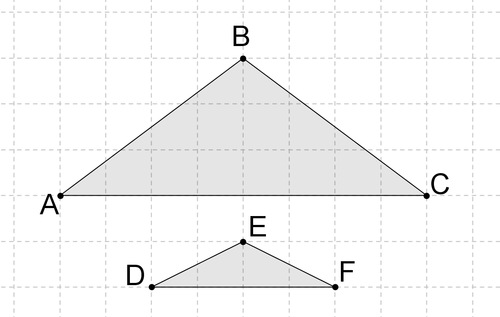
::17. 解释确定两个三角形是否相似的两个方法。

播放段落

18. Assuming the two triangles below are drawn to scale, are they similar? Why or why not? Explain.
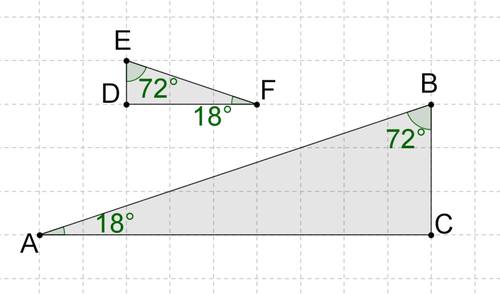
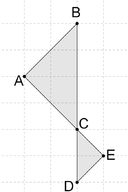
::18. 假设以下两个三角形被拉上尺度,它们是否相似?为什么或为什么没有?解释。

播放段落

19. Assuming the two triangles below are drawn to scale, are they similar? Why or why not? Explain.
::19. 假设以下两个三角形被拉上尺度,它们是否相似?为什么或为什么没有?解释。

播放段落

21. Using interactive geometry software , construct a polygon. Perform the following sequence of transformations in order: a translation, a reflection, a dilation, a rotation, then a second dilation. Is the final image similar to the original? Why or why not? Is there a single dilation that will transform the original into the final image? Why or why not?
::21. 使用交互式几何软件,构建一个多边形。按以下顺序进行变形:翻译、反射、推算、旋转、然后是第二个变形。最后图像是否与原始图像相似?为什么或为什么不?是否有一个变形,可以将原图像转换成最后图像?为什么或为什么不能?

播放段落

22. The triangle below has been dilated by a negative scale factor. Explain what scale factor might be. What sequence of two transformations would also map the original to the image? Are the figures similar? Explain.
::22. 下面的三角形被负比例因素扩大。请解释哪个比例因素可能是比例因素。两种变换的先后顺序也会映射到图像的原始位置?数字是否相似?解释。