Section outline

  • Inscribed Circles of Triangles
    ::被识别的三角圆圈

    Given a triangle , an inscribed circle is the largest circle contained within the triangle . The inscribed circle will touch each of the three sides of the triangle in exactly one point . The center of the circle inscribed in a triangle is the incenter of the triangle, the point where the angle bisectors of the triangle meet.
    ::给定三角形时, 刻入的圆是三角形中包含的最大圆。 刻入的圆将触摸三角形三边的每个点。 三角形中刻的圆的中心是三角形的中间点, 即三角形角对角相交点 。

    Inscribed Circles of Triangles incenter incenter Inscribed Circles of Triangles

    Construct an Inscribed Circle
    ::构造一个归属圆

    This construction assumes you are already familiar with  and  . 
    ::假设你们已经熟悉这个建筑,

    1. Constructing Angle Bisectors
    ::1. 建设角分区

    Draw a triangle. 
    ::绘制三角形。

    Use your compass and straightedge to construct the angle bisector of one of the angles . 
    ::使用您的指南针和直角来构造角度之一的角对角区段 。

    Repeat with a second angle. 
    ::用第二个角度重复 。

    The point of intersection of the angle bisectors is the incenter . It is not necessary to construct all three angle bisectors because they all meet in the same point. The third angle bisector does not provide any new information. 
    ::角对角的分区交叉点是中间点。 没有必要构建所有三个角对角的分区, 因为它们都在同一点相交。 第三个角对角对角的分区不提供任何新信息 。

    2. Constructing a Perpendicular Line
    ::2. 建造直直线

    Use your compass and straightedge to construct a line perpendicular to one side of the triangle that passes through the incenter. 
    ::使用你的指南针和直角 构造一条直直线 直通三角形的一面 穿过中间线

    3. Constructing Inscribed Circle
    ::3. 构建归属圈

    Construct a circle centered at the incenter that passes through the point of intersection of the side of the triangle and the perpendicular line from above. 
    ::构造一个圆, 以圆心为中心, 穿过三角形侧和垂直线的交叉点。

    Note that this circle touches each side of the triangle exactly once. 
    ::请注意,这个圆圈恰好碰过三角形的两侧一次。

    INTERACTIVE
    Inscribed and Circumscribed Circles of Triangles
    minimize icon

    Move the red points to manipulate the triangle and its incenter.
    ::移动红点以操纵三角形及其中枢 。

    Your device seems to be offline.
    Please check your internet connection and try again.
    +
    Do you want to reset the PLIX?
    Yes
    No

    Circumscribed Circles of Triangles
    ::环绕三角圆环

    Given a triangle, the circumscribed circle is the circle that passes through all three vertices of the triangle . The center of the circumscribed circle is the circumcenter of the triangle, the point where the perpendicular bisectors of the sides meet.
    ::在三角形中, 限定的圆圈是穿过三角形所有三个顶端的圆圈。 限定的圆圈的中心是三角形的环绕点, 即两侧的直角两侧相交点 。

    Construct a Circumscribed Circle
    ::构造一个环环形圆

    This construction assumes you are already familiar with . 
    ::这个建筑假设你已经熟悉了。

    1. Constructing Perpendicular Bisectors
    ::1. 建造垂直两侧部门

    Use your compass and straightedge to construct the perpendicular bisector of one side. 
    ::使用你的指南针和直角 建造侧面的垂直双向区段

    Repeat with a second side. 
    ::重复第二面。

    The point of intersection of the is the circumcenter . It is not necessary to construct all three perpendicular bisectors because they all meet at the same point. The third perpendicular bisector does not provide any new information. 
    ::十字路口是环极点。 没有必要建造所有三个垂直两侧区块, 因为它们都在同一点相会。 第三个垂直两侧区块没有提供任何新信息 。

    2. Constructing Circumscribed Circle
    ::2. 建立环环圈

    Construct a circle centered at the circumcenter that passes through one of the vertices of the triangle. This circle should pass through all three vertices . 
    ::构造一个圆, 以圆环为中心, 穿过三角形的顶端之一。 此圆应该穿过所有三个顶端 。

    INTERACTIVE
    Inscribed and Circumscribed Circles of Triangles
    minimize icon

    Move the red points to manipulate  Δ A B C .  
    ::将红点移到操作 ABC 。

    Your device seems to be offline.
    Please check your internet connection and try again.
    +
    Do you want to reset the PLIX?
    Yes
    No

    Examples
    ::实例实例实例实例

    Example 1
    ::例1

    Given a triangle, what's the difference between the  inscribed circle  of the triangle and the  circumscribed circle  of the triangle?
    ::根据三角形,三角形的刻录圆和三角形的限定圆之间有什么区别?

    The inscribed circle of a triangle is inside the triangle. The circumscribed circle of a triangle is outside the triangle.
    ::三角形的刻录圆在三角形内。三角形的限定圆在三角形外。

    Example 2
    ::例2

    Justify the statement: The hypotenuse of a right triangle will be a diameter of the circumscribed circle of the triangle.
    ::说明:右三角形的顺位使用将是三角形的圆形的直径。

    Each of the angles that make up a triangle become inscribed angles of the circumscribed circle. A 90 ∘ angle will intercept an arc of 180 ∘ , which is half a circle. Therefore, the side opposite the  90 ∘ angle of the triangle must be a diameter of the circle.
    ::构成三角形的角中, 每一个角都变成限定圆的刻刻角度。 一个 90 角将拦截半个圆的180 弧。 因此, 三角形的 90 角对面必须是圆形的直径 。

    CK-12 PLIX Interactive
    ::CK-12 PLIX 交互式互动

      Summary
    • An inscribed circle is the largest circle contained within the triangle. The inscribed circle will touch each of the three sides of the triangle in exactly one point.
      ::刻入的圆是三角内包含的最大圆。 刻入的圆将以精确的一点触摸三角内三边的每一个。
    • The incenter is the point where the three angle bisectors of a triangle intersect.
      ::中间点是三角形的三个角对角相交点。
    • The circumscribed circle is the circle that passes through all three vertices of the triangle.
      ::限定的圆圈是穿过三角形所有三个顶端的圆圈。

    Review
    ::审查审查审查审查

    1. Draw a triangle and construct the angle bisector of two of its angles.
    ::1. 绘制三角形,并构造其两个角角的角对角。

    2. Continue with your triangle from #1. Construct a line perpendicular to one side of the triangle that passes through the incenter of the triangle.
    ::2. 继续使用您在 # 1 中的三角形 。 构造一条直直直线到三角形的一面, 穿过三角形的中点 。

    3. Continue with your triangle from #1 and #2. Construct the inscribed circle of the triangle.
    ::3. 从 #1 和 #2 继续您的三角形, 构造三角形的刻录圆 。

    4. Why was it not necessary to construct the angle bisector of all three of the angles of the triangle?
    ::4. 为什么没有必要构建三角形所有三个角的角角对角区?

    5. Explain why the incenter is equidistant from each of the sides of the triangle.
    ::5. 解释为什么中间线离三角形两侧的距离相等。

    6. Draw a triangle and construct the perpendicular bisector of two of its sides.
    ::6. 绘制三角形,构筑两侧的垂直双侧。

    7. Continue with your triangle from #5. Construct the circumscribed circle of the triangle.
    ::7. 从#5. 继续使用三角形构建三角形的限定圆。

    8. Explain why the circumcenter is equidistant from each of the vertices of the triangle.
    ::8. 解释一下为什么环中点与三角形的每个顶端的距离相等。

    You work selling food from a food truck at a local park. You want to position your truck so that it is the same distance away from each of the three locations shown on the map below.
    ::你的工作是在当地公园卖食品卡车的食物,你想把卡车定位在距离地图下显示的三个地点的距离相同的地方。

    Map showing locations of a basketball court, playground, and parking lot for distance analysis.

    9. Is the point of interest the incenter or the circumcenter?
    ::9. 利害关系是中枢还是中枢?

    10. Find the point on the map that is equidistant from each of the three locations.
    ::10. 在地图上找到三个地点中每个地点相距相等的点。

    11. How could you fold the map in two places to find the point equidistant from each of the three locations?
    ::11. 如何将地图折叠成两个地方,从三个地点中找到等距点?

    A new elementary school is to be constructed in your town. The plan is to build the school so that it is the same distance away from each of the three major roads shown in the map below.
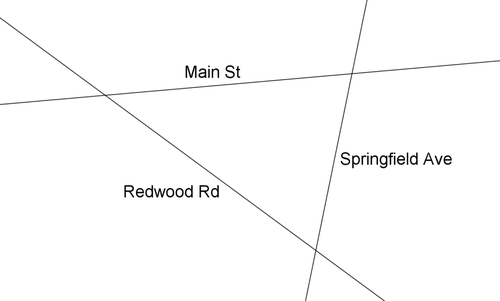
    ::计划在你的城镇新建一所小学,计划建造这所学校,以便与下图显示的三条主要道路的每条距离相同。

    Map showing three major roads intersecting, related to finding equidistant points.

    12. Is the point of interest the incenter or the circumcenter?
    ::12. 利害关系是中枢还是中枢?

    13. Find the point on the map that is equidistant from each of the three roads.
    ::13. 在地图上找到从三条道路中每一条道路上相等的位置。

    14. How could you fold the map in two places to find the point equidistant from each of the three roads?
    ::14. 你怎么能把地图折叠成两个地方,从三条道路的每个道路上找到等距点?

    15. Justify the following statement: Given any three non-collinear points, there exists exactly one circle that passes through the points.
    ::15. 说明如下:鉴于任何三个非两极点,完全有一个圆圈穿过三极点。

    16. A sprinkler is being installed in the park. The park is in the shape of a triangle with sidewalks along each side of the park. Draw a diagram to represent this problem and use your knowledge of inscribed circles to determine where the sprinkler should be placed in order to keep the ground wet and the sidewalks dry.
    ::16. 公园正在安装一个喷洒器,公园的形状是三角形,沿公园的两侧都有人行道,绘制一个图来说明这个问题,并利用你对刻着圆圈的了解来确定喷洒器应放在何处,以便保持地面湿润和人行道干燥。

    17. In the amusement park, lines joining the Ferris wheel, the roller coaster, and the carousal make a triangle. You want to put a refreshment stand in the park that is equidistant between these three attractions. Construct a circle that has the intersection of the perpendicular bisectors of the triangle (the circumcenter) as it center. Describe the relationship between the triangle and the circle.
    ::17. 在游乐园中,连接Ferris轮轮、滚轮滑轮和旋转木马的线条形成三角形。您想要在公园中设置一个在这三个景点之间等距的复习台。 构造一个圆形, 该圆形以三角形( 环绕中心) 的垂直双形为中心。 描述三角形和圆形之间的关系 。

    18. Using the information in question 17, if the vertices of the triangle are moved to change the shape and size, how will this affect the relationship between the circle and the triangle?
    ::18. 利用问题17中的信息,如果三角形的顶端被移动以改变形状和大小,这将如何影响圆与三角之间的关系?

    Review (Answers)
    ::审查(答复)

    Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
    ::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。