Section: 圆圈中指定的四边形 | 8.6 圆圈中设定的四方-interactive

Section outline

A quadrilateral is said to be inscribed in a circle if all four vertices of the quadrilateral lie on the circle. Quadrilaterals that can be inscribed in circles are known as cyclic quadrilaterals. The quadrilateral below is a cyclic quadrilateral.
::如果四边形的所有四个顶点都位于圆上,则四边形被刻在一个圆圈中。圆圈中可以刻入圆圈的四边形被称为环形四边形。下面的四边形是环形四边形。

Not all quadrilaterals can be inscribed in circles and so not all quadrilaterals are cyclic quadrilaterals. A quadrilateral is cyclic if and only if its opposite angles are supplementary .
::并非所有的四边形都可被刻在圆圈中,因此并非所有的四边形都是环形四边形。四边形是环形四边形的,如果而且只有在相反角度是辅助性的,四边形是环形的。

Proving Supplementary Angles
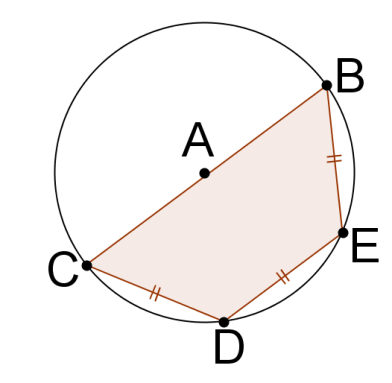
::证明补充角

Consider the cyclic quadrilateral below. Prove that $\begin{align*}\angle DEB \end{align*}$ and $\begin{align*}\angle DCB\end{align*}$ are supplementary .
::考虑下方的圆四边形。证明 DEB 和 DCB 是补充的。

First note that $\begin{align*}m \widehat{DEB} + m \widehat{DCB}=360^\circ\end{align*}$ because these two arcs make a full circle. $\begin{align*}2m \angle DEB = m \widehat{DCB}\end{align*}$ and $\begin{align*}2m \angle DCB = m \widehat{DEB}\end{align*}$ because the measure of an inscribed angle is half the measure of its intercepted arc . By substitution, $\begin{align*}2m \angle DEB + 2m \angle DCB = 360^\circ\end{align*}$ . Divide by 2 and you have $\begin{align*}m \angle DEB + m \angle DCB = 180^\circ\end{align*}$ . Therefore, $\begin{align*}\angle DEB\end{align*}$ and $\begin{align*}\angle DCB\end{align*}$ are supplementary.
::第一个注意是 mDEB+mDCB=360,因为这两个弧是一个圆圈。 2mDEB=mDCB=mDCB和2mDCB=mDEB,因为一个刻入角的测量量是其截取弧的半分之一。2mDEB+2mDCB=360。除以2,你有 mDEB+mDCB=180。因此, DEB和DCB是补充的。

Finding Contradictions
::查找不一致之处

Consider the quadrilateral below. Assume that $\begin{align*}\angle B\end{align*}$ and $\begin{align*}\angle F\end{align*}$ are supplementary, but note that point $\begin{align*}F\end{align*}$ does NOT lie on the circle. Find a contradiction. What does this prove?
::考虑下方的四边形。假设B 和F 是补充的, 但请注意点F 不存在于圆圈上。找出一个矛盾。这证明什么 ?

One method of proof is called a proof by contradiction . With a proof by contradiction you prove that something cannot not be true. Therefore, it must be true. Here, you are attempting to prove that it is impossible for a quadrilateral with opposite angles supplementary to not be cyclic. Therefore, such a quadrilateral must be cyclic.
::一种证明方法被称作矛盾的证明。如果用矛盾的证明来证明某事不可能是真实的。因此,它必须是真实的。在这里,你试图证明一个具有相反角度的四边形不可能是循环的。因此,这样的四边形必须是循环的。

Finding a Point of Intersection
::寻找交叉点

Assume that $\begin{align*}\angle B\end{align*}$ and $\begin{align*}\angle F\end{align*}$ are supplementary, but note that point $\begin{align*}F\end{align*}$ does not lie on the circle. Find the point of intersection of $\begin{align*}\overline{EF}\end{align*}$ and the circle and call it point $\begin{align*}D\end{align*}$ . Form a segment by connecting point $\begin{align*}D\end{align*}$ with point $\begin{align*}C\end{align*}$ .
::假设 {B\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\"B\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\

$\begin{align*}\angle CDE \end{align*}$ is an exterior angle of $\begin{align*}\triangle FCD\end{align*}$ , so its measure is equal to the sum of the measures of the remote interior angles of the triangle . This means that $\begin{align*}m \angle CDE = m \angle FCD + m \angle F\end{align*}$ . Quadrilateral $\begin{align*}BCDE\end{align*}$ is cyclic, so $\begin{align*}\angle CDE\end{align*}$ and $\begin{align*}\angle B\end{align*}$ must be supplementary. This means that $\begin{align*}\angle CDE\end{align*}$ and $\begin{align*}\angle F\end{align*}$ must be congruent because they are both supplementary to the same angle. However, since $\begin{align*}\angle CDE\end{align*}$ and $\begin{align*}\angle F\end{align*}$ are not congruent (it is a contradiction), the assumption that $\begin{align*}\angle B\end{align*}$ and $\begin{align*}\angle F\end{align*}$ are supplementary must be false.
::CDE 是 QFCD 的外部角度, 所以它的度量等于三角形的远程内角的度量总和。这意味着 mQCDE= mQFCD+mQQF. 四方 BDE 是循环的, 所以 QCDE 和 QB 必须是补充的。这意味着 QCDE 和 QF 必须是相近的, 因为它们都是对同一角度的补充。但是, QCDE 和 QF 不是相匹配的( 这是矛盾的), 认为 QB 和 QF 是补充的假设必须是虚假的。

Note: You will learn more about proof by contradiction in future courses!
::说明: 未来课程中, 你会通过自相矛盾来了解更多证据!

Solving for Unknown Values
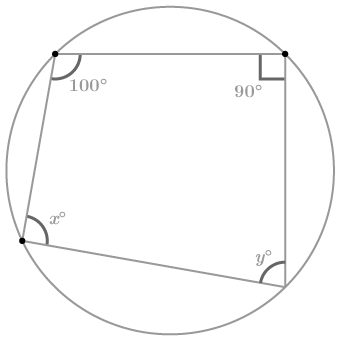
::解决未知值

Solve for $\begin{align*}x\end{align*}$ and $\begin{align*}y\end{align*}$ .
::解决x和y。

Quadrilateral inscribed in a circle with angles labeled 100°, 90°, x°, and y°.

Opposite angles are supplementary,
::对角是补充的,

$\begin{align*}\text{so}, \ 90^\circ + x^\circ & = 180^\circ \\ x^\circ & = 180^\circ - 90^\circ \\ x^\circ & = 90^\circ \\ \text{Similarly}, \ 100^\circ + x^\circ & = 180^\circ \\ x^\circ & = 180^\circ - 100^\circ \\ x^\circ & = 80^\circ\end{align*}$
::90x180x80x80 90x90Symilarly,100x180x180x180 180x80}100x180x80

This means $\begin{align*}x=90\end{align*}$ and $\begin{align*}y=80\end{align*}$ .
::这意味着 x=90和y=80。

Examples
::实例实例实例实例

Example 1
::例1

One angle of a rhombus is $\begin{align*}30^\circ\end{align*}$ . Can this rhombus be inscribed in a circle?
::暴风雨的一个角度是 30 。这个暴风雨可以被刻在圆形里吗 ?

Opposite angles of a rhombus are congruent. If a rhombus has a $\begin{align*}30^\circ\end{align*}$ angle then it has one pair of opposite angles that are each $\begin{align*}30^\circ\end{align*}$ and one pair of opposite angles that are each $\begin{align*}150^\circ\end{align*}$ . Opposite angles are not supplementary so this rhombus cannot be inscribed in a circle.
::暴风车的对角是相似的。如果暴风车有一个 30 angle, 那么它就有一对对对角, 每30 和一对对对角, 每150 。对角不具有补充作用, 因此无法将暴风车刻入圆圈。

Example 2
::例2

i) Find $\begin{align*}m \widehat{DE}\end{align*}$ .
:一) 寻找mDE。

$\begin{align*}\angle BCD\end{align*}$ is the inscribed angle of $\begin{align*}\widehat{DEB}\end{align*}$ . This means that the measure of the arc is twice the measure of the angle. $\begin{align*}m \angle DEB\end{align*}$ $\begin{align*}= 2 \cdot \angle BCD=2 \cdot 87^\circ = 174^\circ\end{align*}$ . Since $\begin{align*}m \widehat{BE}\end{align*}$ $\begin{align*}=76^\circ\end{align*}$ , $\begin{align*}m \widehat{DE}=m \widehat{DEB} - m \widehat{BE} = 174^\circ - 76^\circ = 98^\circ\end{align*}$ .
::BCD 是 DEB 的刻度角。这意味着弧的量度是角度的两倍。 mDEB= 2BCD= 287174。自 mBE= 76, mDE= mDEB- mB= 1747698\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\DEDEDEBBB\ mBBBBBE= = 17476\\\\\\\\\\\\\\\ 98\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\ 。

ii) Find $\begin{align*}m \angle DEB\end{align*}$ .
:二) 找到MDEB。

$\begin{align*}\angle BCD\end{align*}$ and $\begin{align*}\angle DEB\end{align*}$ are opposite angles of a cyclic quadrilateral so they are supplementary. $\begin{align*}m \angle DEB = 180^\circ - \angle BCD = 180^\circ - 87^\circ = 93^\circ\end{align*}$ .
::BCD和DEB是圆形四边形的对角。 mDEB=180BCD=1808793。

iii) Find $\begin{align*}m \widehat{CB}\end{align*}$ .
:三) 寻找MCB。

A full circle is $\begin{align*}360^\circ\end{align*}$ .
::整个圆圈是360。

$\begin{align*}m \widehat{CB} & =360^\circ - m \widehat{CD} - m \widehat{DE} - m \widehat{BE}\\ & = 360^\circ - 60^\circ - 98^\circ - 76^\circ \\ & = 126^\circ\end{align*}$ .
::=360mCD-mDE-mBE=360609876126。

CK-12 PLIX: Inscribed Quadrilaterals in Circles
::CK-12 PLIX: 圆圆中给定的四边形

Summary

A quadrilateral is said to be inscribed in a circle if all four vertices of the quadrilateral lie on the circle.
::据说,如果四边形的所有四个顶点都在圆上,则四边形将被刻在圆内。

Quadrilaterals that can be inscribed in circles are known as cyclic quadrilaterals . A quadrilateral is cyclic if and only if its opposite angles are supplementary.
::可以刻在圆圈中的四边形称为圆形四边形。四边形是圆形的,如果而且只有在相反角度是补充的时才是圆形。

A proof by contradiction is an indirect proof takes the conclusion from a hypothesis and assumes it is false until a contradiction is reached, thus proving the original hypothesis is true.
::矛盾的证据是间接证据,从假设中得出结论,并假定在出现矛盾之前是虚假的,从而证明原来的假设是真实的。

Review
::审查审查审查审查

1. What is a cyclic quadrilateral?
::1. 什么是环形四边形?

2. A quadrilateral is cyclic if and only if its opposite angles are __________________.
::2. 一个四边形是环形的,如果而且只有在其相反角度是。

3. Find $\begin{align*}m \angle B\end{align*}$ .
::3. 寻找mB。

4. Find $\begin{align*}m \angle E\end{align*}$ .
::4. 寻找mE。

5. Find $\begin{align*}m \angle D\end{align*}$ .
::5. 寻找MQD。

Quadrilateral ABCDE inscribed in a circle with points marked on its vertices.

6. Find $\begin{align*}m \widehat{CD}\end{align*}$ .
::6. 寻找 mCD。

7. Find $\begin{align*}m \widehat{DE}\end{align*}$ .
::7. 寻找市场。

8. Find $\begin{align*}m \angle CBE\end{align*}$ .
::8. 寻找mCBE。

9. Find $\begin{align*}m \angle CEB\end{align*}$ .
::9. 寻找MZCEB。

Graphic showing a circle with a quadrilateral and angle expressions for calculation.

10. Solve for $\begin{align*}x\end{align*}$ .
::10. 解决x.

11. Solve for $\begin{align*}y\end{align*}$ .
::11. 解决y.

12. Solve for $\begin{align*}x\end{align*}$ .
::12. 解决x.

13. Solve for $\begin{align*}y\end{align*}$ .
::13. 解决y.

14. If a cyclic quadrilateral has a $\begin{align*}90^\circ\end{align*}$ angle, must it be a square? If yes, explain. If no, give a counter example.
::14. 如果圆形四边形有90角,必须是一个方形吗?如果有,请解释。如果有,请举一个反例。

15. Use the picture below to prove that angles $\begin{align*}B\end{align*}$ and $\begin{align*}D\end{align*}$ must be supplementary.
::15. 利用下面的图景来证明角度B和D必须是补充性的。

16. Describe a real world logo that has a quadrilateral inscribed in a circle.
::16. 描述一个在圆形上刻有四边形的真正的世界标志。

17. A stained glass ornament is in the shape of a circle. The artist would like to inscribe quadrilaterals into the circle. Draw three different designs for her and describe the kinds of quadrilaterals she needs to make for each one.
::17. 彩色玻璃装饰品是圆形的形状,艺术家希望在圆圈中加入四边形,为她绘制三个不同的设计图,描述她为每个圆圈需要做的四边形。

Review (Answers)
::审查(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

Section outline

Proving Supplementary Angles ::证明补充角

Finding Contradictions ::查找不一致之处

Finding a Point of Intersection ::寻找交叉点

Solving for Unknown Values ::解决未知值

Examples ::实例实例实例实例

Example 1 ::例1

Example 2 ::例2

CK-12 PLIX: Inscribed Quadrilaterals in Circles ::CK-12 PLIX: 圆圆中给定的四边形

Review ::审查审查审查审查

Review (Answers) ::审查(答复)