Section: 弧弧长度 | 8.9弧长度-interactive

Section outline

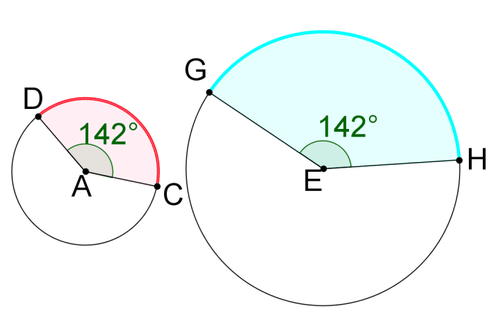
Recall that a portion of a circle is called an arc . One way to measure an arc is with degrees. The measure of an arc is equal to the measure of its corresponding central angle . Below, $\begin{aligned} m \hat{D C} \end{aligned}$ $\begin{aligned} = 70^{\circ} \end{aligned}$ and $\begin{aligned} m \hat{G H} \end{aligned}$ $\begin{aligned} = 70^{\circ} \end{aligned}$ .
::回顾圆的某一部分被称为弧。测量弧的一种方式是用度来测量弧。弧的度量与其相应的中心角的度量相等。以下是 mDC70和 mGH70。

When you measure an arc in degrees, it tells you the relative size of the arc compared to the whole circle. It does not tell you anything about the absolute size of the arc or the circle it came from. Both arcs above have the same measure, but $\begin{aligned} \hat{G H} \end{aligned}$ is physically longer , due to circle $\begin{aligned} E \end{aligned}$ being bigger.
::当用度量一个弧时, 它会告诉你弧相对于整个圆的相对大小。它不会告诉你弧的绝对大小或圆的来源。上面的两个弧都有相同的量度, 但是由于圆 E更大, GH 物理上更长。

This leads to another way of describing the size of an arc. Arc length measures the distance (in units such as inches or centimeters) along a circle between the endpoints that define the arc. Above, $\begin{aligned} \hat{G H} \end{aligned}$ has a greater arc length than $\begin{aligned} \hat{D C} \end{aligned}$ . Because the radius of a circle is what determines the circle's size, the length of an arc intercepted by a given angle will be directly proportional to the radius of the circle.
::这导致描述弧大小的另一种方式。弧长度测量点之间圆形的距离( 单位, 如英寸或厘米) 。上面, GH 的弧长度大于 DC 。因为圆的半径决定圆的大小, 以给定角度截取的弧长度将与圆半径成正比。

Arc length suggests a new way of in circles. Previously, you have measured all angles in degrees, but you can also measure angles in radians. 1 radian is the angle that creates an arc that has a length equal to the radius . Below, the arc has a length equal to the radius. The angle that is created is 1 radian .
::弧长度指向圆圈中的一种新方式。以前,您用度来测量所有角度,但也可以用弧度来测量角度。 1 弧度是创建与半径相等的弧度角的角。以下,弧值的长度与半径相等。创建的角度为 1 弧度。

You can use the formula for the of a circle to show that there are $\begin{aligned} 2 π \end{aligned}$ radians in a circle (You will justify this in the Examples). This means that:
::您可以使用圆形的公式来显示圆内有 2+ 弧度(您可以在示例中说明这一点)。这意味着 :

$\begin{aligned} 2 π radians = 360^{\circ} \end{aligned}$
::2 弧度= 360 {____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

Therefore, you have the following conversions:
::因此,您有以下转换:

$\begin{aligned} 1 radian & = (\frac{180}{π}) degrees (\approx {57.3}^{\circ}) \\ 1 degree & = (\frac{π}{180}) radians (\approx 0.17 radians) \end{aligned}$
::1弧度=( 180) 度 (57.3) 1度=( 180) 弧度 (0. 17 弧度)

Note that if a given angle has no units, it is assumed to be in radians.
::请注意,如果给定角没有单位,则假定为弧度。

A sector is a portion of a filled circle bounded by two radii and an arc (a “wedge” of a circle).
::一个扇形是两个弧形和弧形(圆形的“网形”)交界的填充圆圈的一部分。

Let's do a problem involving sector similarity.
::让我们处理一个部门相似性的问题

Show that two sectors with the same central angle are similar by using transformations to explain why the two shaded sectors below are similar.
::显示两个具有相同中心角的区块相似, 使用变换来解释下面两个阴影区块相似的原因。

Two shapes are similar if a similarity transformation exists between them. Draw a vector from point $\begin{aligned} A \end{aligned}$ to point $\begin{aligned} E \end{aligned}$ . Translate the gray sector along the vector.
::如果两个形状之间存在相似性变换,则两个形状相似。从 A 点到 E 点绘制矢量。沿矢量翻转灰色部分。

Rotate the image so that $\begin{aligned} \bar{E C^{'}} \end{aligned}$ lies on $\begin{aligned} \bar{E H} \end{aligned}$ . Because angles are preserved with translations and rotations , the image of $\begin{aligned} \bar{E D^{'}} \end{aligned}$ will lie on $\begin{aligned} \bar{E G} \end{aligned}$ .
::旋转图像, 使 EH 位于 EH 上。因为角度由翻译和旋转保存, ED 图像将位于 EG 上。

Dilate the image about point $\begin{aligned} E \end{aligned}$ by a factor of $\begin{aligned} \frac{E H}{A C} \end{aligned}$ .
::将 E 点的图像扩大为 EHAC 系数。

The two sectors are similar because a sequence of rigid transformations followed by a dilation carried one sector to the other .
::这两个部门相似,因为一连串的僵硬转变,然后一个部门与另一个部门进行推算。

Next, let's look at a problem involving arc length.
::接下来,让我们来看看一个问题涉及弧长度。

Explain why the length of arc $\begin{aligned} s \end{aligned}$ is equal to $\begin{aligned} θ r \end{aligned}$ , where $\begin{aligned} θ \end{aligned}$ is the central angle in radians and $\begin{aligned} r \end{aligned}$ is the radius of the circle.
::解释为什么弧 s 的长度等于 °r, 其中 °是弧度的中心角, r 是圆的半径。

In a circle of radius 1, the measure of a central angle in radians will be equal to the length of the intercepted arc . This is because the number of radians equals the number of radii that make up the arc.
::在半径 1 的圆形中,以弧度表示的中心角的测量量将等于被截取弧的长度。这是因为弧度数等于构成弧的弧度的弧度数。

Three sectors with different central angles labeled in radians, showing relationships between arc lengths.

If a sector has radius $\begin{aligned} r \end{aligned}$ , it is similar to a sector of radius 1 with the same central angle (as shown in the previous problem about sectors).
::如果某一区段的半径为r,它与半径1的同一中心角的区段相似(如以前关于区段的问题所示)。

Because the sectors are similar, corresponding lengths are proportional:
::由于部门相似,相应的长度是成比例的:

$\begin{aligned} \frac{r}{1} & = \frac{s}{x} \\ s & = x r \end{aligned}$
::r1 =sxs=xr =sxs=xr =xr =xr =xs=xr =xr =xs=xr =xs=xr

$\begin{aligned} x \end{aligned}$ must be equal to the measure of $\begin{aligned} θ \end{aligned}$ in radians. Therefore:
::x 必须等于 ° 的弧度。因此 :

$\begin{aligned} s = θ r \end{aligned}$
::sr

Why does this make sense? Remember that if $\begin{aligned} θ \end{aligned}$ is in radians, then $\begin{aligned} θ \end{aligned}$ is equal to the number of radii that fit around the arc. The number of radii that fit around the arc multiplied by the length of the radius will equal the length of the arc.
::这为什么有意义?记住,如果是弧度,那么等于弧周围的弧度数。环弧周围的弧度乘以半径长度的弧度数将等于弧的长度。

Arc Length
::弧弧长度

Play with a circle by dragging one of the points that define the endpoints of the arc. The arc length is recalculated as you drag.
::拖曳一个点来定义弧的终点,以此来玩圆。拖动时,弧的长度会重新计算。

Finally, lets look at a problem where we measure arc length.
::最后,让我们看看我们衡量弧长度的问题。

Find $\begin{aligned} m \hat{G H} \end{aligned}$ in radians and the length of $\begin{aligned} \hat{G H} \end{aligned}$ .
::以弧度和GH 长度查找 mGH 。

$\begin{aligned} m \hat{G H} = 106^{\circ} \end{aligned}$ .
::{\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}我...

Remember that $\begin{aligned} 1 degree = (\frac{π}{180}) radians \end{aligned}$ . This means that $\begin{aligned} 106^{\circ} = 106 \cdot (\frac{π}{180}) \approx 1.85 radians \end{aligned}$ .
::记住 1 度= (180) 弧度。这意味着 106 106 (180) 1.85 弧度。

Now you can find the length of the arc. To find the length of the arc, multiply the radius (6 in) by the measure of the central angle in radians.
::现在,您可以找到弧的长度。要找到弧的长度,请以弧度衡量中心角的弧度乘以半径(6英寸)。

$\begin{aligned} s & = θ r \\ s & = (1.85) (6) \\ s & \approx 11.1 in \end{aligned}$
::srs=( 1. 85(6)s11.1 英寸)

Don't forget that your angle must be in radians in order to use the formula $\begin{aligned} s = θ r \end{aligned}$ !
::不要忘了,你的角度必须是弧度才能使用公式sr!

Examples
::实例实例实例实例

Example 1
::例1

There are $\begin{aligned} 360^{\circ} \end{aligned}$ in a circle and $\begin{aligned} 90^{\circ} \end{aligned}$ in a right angle . How many radians are in a circle and how many radians make up a right angle?
::圆形中为 360 圆形,右角中为 90 。圆形中有多少弧度,右角中有多少弧度?

There are $\begin{aligned} 2 π \end{aligned}$ radians in a circle. A right angle is $\begin{aligned} 90^{\circ} \end{aligned}$ and $\begin{aligned} 90^{\circ} \end{aligned}$ is $\begin{aligned} \frac{1}{4} \end{aligned}$ of a circle, so there are $\begin{aligned} \frac{2 π}{4} = \frac{π}{2} \end{aligned}$ radians in a right angle.
::圆内有 2 弧度。右角是 90 和 90 is 14 圆, 因此右角有 2 4 2 弧度。

Example 2
::例2

Explain why a circle has $\begin{aligned} 2 π radians \end{aligned}$ .
::解释为什么圆有2弧度。

The circumference of a circle with radius 1 is $\begin{aligned} 2 π (1) = 2 π \end{aligned}$ . Therefore, $\begin{aligned} 2 π \end{aligned}$ radii fit around a circle with radius 1. All circles are similar, so $\begin{aligned} 2 π \end{aligned}$ radii must fit around all circles. 1 radian is the angle that creates an arc that has a length equal to the radius, so $\begin{aligned} 2 π \end{aligned}$ radians is the angle that creates an arc with a length equal to $\begin{aligned} 2 π \end{aligned}$ radii. Therefore, a circle is $\begin{aligned} 2 π \end{aligned}$ radians because $\begin{aligned} 2 π \end{aligned}$ radii fit around any circle.
::半径 1 的圆环环为 2(1)=2。因此, 2 弧度适合半径 1 的圆圈周围。所有圆圈都相似, 所以 2 弧度必须适合所有圆圈周围。 1 弧度是产生弧度与半径长度相等的弧角的角, 因此 2 弧度是产生弧度等于 2 弧度的角。因此, 一个圆圈是 2 弧度, 因为 2 弧度适合任何圆圈周围的弧。

Example 3
::例3

How many radians are there in $\begin{aligned} 150^{\circ} \end{aligned}$ ?
::150中有多少弧度?

Remember that $\begin{aligned} 1 degree = (\frac{π}{180}) radians \end{aligned}$ . This means that $\begin{aligned} 150^{\circ} = 150 \cdot (\frac{π}{180}) \approx 2.62 radians \end{aligned}$ .
::记住 1 度= (180) 弧度。这意味着 150 150 (180) 2.62 弧度。

Example 4
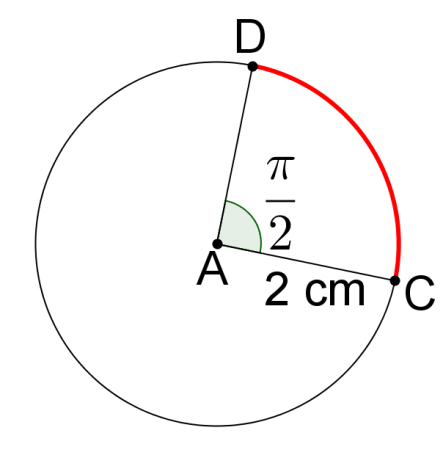
::例4

Find the length of $\begin{aligned} \hat{C D} \end{aligned}$ .
::查找 CD 的长度。

Circle diagram showing angle A with 150° and radius AC measuring 4 cm.

$\begin{aligned} s = θ r \end{aligned}$ and $\begin{aligned} θ = 150^{\circ} = 150 \cdot (\frac{π}{180}) \approx 2.62 radians \end{aligned}$ .
::1501501802.62弧度

The length of $\begin{aligned} \hat{C D} \end{aligned}$ is $\begin{aligned} s = (2.62) (4) \approx 10.48 cm \end{aligned}$ .
::CD 的长度为 s= (2.62)(4) 10.48 cm 。

CK-12 PLIX Interactive
::CK-12 PLIX 交互式互动

Summary

An arc is a section of the circumference of a circle.
::弧是圆环绕的一部分。

A radian is a unit of angle that is equal to the angle created at the center of a circle whose arc is equal in length to the radius.
- 1 radian $\begin{aligned} = (\frac{180^{\circ}}{π}) degrees \end{aligned}$
  ::1弧度 = (180) 度
- 1 degree $\begin{aligned} = (\frac{π}{180^{\circ}}) radian \end{aligned}$
  ::1 度= (180) 弧度
::弧度是一个角度单位,等于在圆的中心所设定的角,圆弧长度等于半径。 1 弧度=( 180) 1度=( 180) 1度=( 180) 弧度=( 180) 弧度

Review
::审查审查审查审查

1. What's the difference between finding the measure of an arc and the length of an arc?
::1. 找到弧的量度与弧的长度有什么区别?

2. What is the relationship between a radian and a radius?
::2. 弧度和半径之间的关系是什么?

3. How are radians and degrees related?
::3. 弧度和度如何相关?

4. Explain why the two shaded sectors below are similar.
::4. 解释以下两个阴影部门为何相似。

5. Justify why the length of arc $\begin{aligned} s \end{aligned}$ is equal to $\begin{aligned} θ r, \end{aligned}$ where $\begin{aligned} θ \end{aligned}$ is the central angle in radians and $\begin{aligned} r \end{aligned}$ is the radius of the circle.
::5. 说明弧 s 的长度为何等于 °r, 其中 °是弧度的中心角, r 是圆的半径。

Convert each angle measured in degrees to an angle measured in radians. Leave answers in terms of $\begin{aligned} π . \end{aligned}$
::将以度度测量的每个角度转换为以弧度测量的角。请按 ° 表示回答。

6. $\begin{aligned} 180^{\circ} \end{aligned}$

7. $\begin{aligned} 360^{\circ} \end{aligned}$

8. $\begin{aligned} 90^{\circ} \end{aligned}$

9. $\begin{aligned} 60^{\circ} \end{aligned}$

10. $\begin{aligned} 30^{\circ} \end{aligned}$

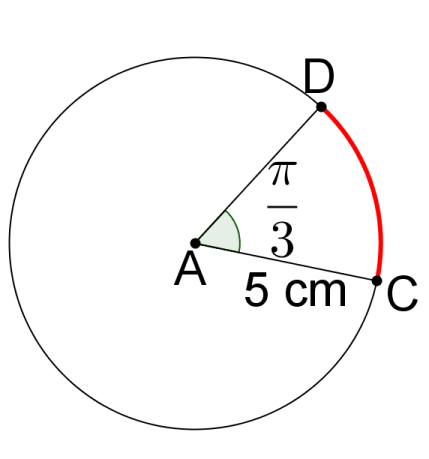
Find the measure in degrees and length in centimeters of $\begin{aligned} \hat{C D} \end{aligned}$ in each circle.
::在每个圆圈中查找以 CD 度和长度厘米计的量度和长度。

11.

12.

13.

14.

15. Explain how to find the length of an arc when given the central angle in radians. How does this compare to the process of finding the length of an arc when given the central angle in degrees?
::15. 当给定弧以弧度为中心角时,解释如何找到弧的长度,这与给定以度为中心角时查找弧的长度的过程相比如何?

16. Sheldon's grandmother made a strawberry-rhubarb pie for he and his six friends. He cut a piece that had a crust length of 3 inches. If each person gets an identical sized piece, what is the circumference and diameter of the pie?
::16. Sheldon的祖母为他和他的六个朋友做了一个草莓胡巴派。他切了一块外壳长度为3英寸的肉片。如果每人得到一块大小相同的肉片,那饼的周长和直径是多少?

17. A stop sign is in the shape of a regular octagon. If it was inscribed in a circle, how could you determine the measure for each arc? Explain your reasoning. How would your determination change if you had a school zone sign which is in the shape of a regular pentagon?
::17. 停止符号的形状是正八角形,如果将其刻在圆形内,您如何确定每个弧的量度?解释你的推理。如果您有一个普通五角形的校区符号,您的决心会如何改变?

Review (Answers)
::审查(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

Section outline

Arc Length ::弧弧长度

Examples ::实例实例实例实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

CK-12 PLIX Interactive ::CK-12 PLIX 交互式互动

Review ::审查审查审查审查

Review (Answers) ::审查(答复)