金锥体和锥体

播放段落

Recall that a pyramid is a solid with a polygon base and triangular lateral faces that meet in a vertex . Pyramids are named by their base shape.
::记得金字塔是一个坚固的金字塔,有多边形基和三角横向面,在顶端相交。金字塔按其底形命名。

播放段落

You have seen the formula for the of a pyramid before.
::你以前见过金字塔的配方

播放段落

$\begin{array}{r}{V}_{\text{pyramid}}=\frac{A_{\text{base}}\cdot h}{3}\end{array}$
::Vpyramid=Abase_h3 甚金字塔=Abase_h3

播放段落

Where does this formula come from? Recall that to find the volume of a prism or a cylinder , you need to find the area of the base and multiply by the height .
::此公式来自何方? 回顾要找到棱晶或圆柱体的体积, 您需要找到基数区域, 并乘以高度 。

播放段落

$\begin{array}{r}{V}_{\text{prism}}=A_{\text{base}}\cdot h\end{array}$
::瓦基斯=阿巴萨

播放段落

The difference between these two formulas is the division by 3. The key to understanding where the 3 comes from is remembering Cavalieri's principle and investigating a square based pyramid.
::这两种公式的区别是3比3,理解3的关键在于记住卡瓦列里尼的原则并调查一个平方形金字塔。

播放段落

Let's take a look at some problems involving pyramids.
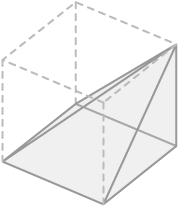
::让我们来看看金字塔的一些问题

播放段落

1. The two square pyramids below are each constructed within cubes of the same size. The pyramid on the left has a vertex at the center of a face of the cube. The pyramid on the right has a vertex at one of the vertices of the cube. Is the volume of each pyramid the same?
::1. 以下两个方形金字塔都是在相同大小的立方体内建造的,左边的金字塔在立方体面中心有一个顶点,右边的金字塔在立方体顶部之一有一个顶点。

播放段落

Because each pyramid is constructed within the same cube, the heights of the pyramids are the same and the areas of their bases are the same. When a plane parallel to the base of the pyramid is constructed through the center of each cube, the cross sections of each pyramid are the same.
::因为每个金字塔都是在同一个立方体内建造的,所以金字塔的高度是一样的,其基底的高度也是一样的。 当一个与金字塔底部平行的平面通过每个立方体的中心建造时,每个金字塔的交叉部分是相同的。

播放段落

Each cross section is a square . The length of the side of the square is half the length of an edge of the original cube, since the plane was constructed through the middle of the cube.
::每个截面区域都是一个正方形。正方形的侧面长度是原立方体边缘长度的一半,因为平面是通过立方体中间构造的。

播放段落

Because cross sections are the same area, heights are the same, and bases are the same, these pyramids must have the same volume due to Cavalieri's principle.
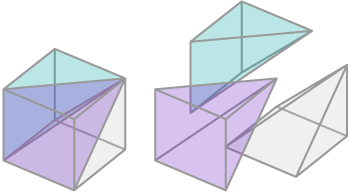
::由于交叉区域相同,高度相同,基数相同,这些金字塔的体积因卡瓦列里尼原则而必须相同。

播放段落

2. How many square based pyramids congruent to the one below would it take to fill the cube? Can you visualize this?
::2. 填充立方体需要多少平方基金字塔,与下面的金字塔一致?你能想象到吗?

播放段落

It will take exactly 3 congruent pyramids to fill the cube. The image below shows each pyramid being added to the cube.
::填充立方体需要3个完全相同的金字塔。下面的图像显示每个加入立方体的金字塔。

播放段落

3. Use the answers from the previous problems to explain why the volume of a pyramid is $\begin{array}{r}{V}_{\text{pyramid}}=\frac{A_{\text{base}}\cdot h}{3}\end{array}$ .
::3. 利用以前问题的答案来解释为什么金字塔的体积是Vpyramid=Abase_h3。

播放段落

The volume of a rectangular prism is $\begin{array}{r}{A}_{\text{base}}\cdot h\end{array}$ . This is because $\begin{array}{r}{A}_{\text{base}}\end{array}$ gives the volume of one "layer", and multiplying by the height scales that base volume by the number of "layers" of the prism.
::矩形棱柱的体积是 Abase_h。 这是因为 Abase 给出一个“ 层” 的体积, 并且乘以基体体积的高度尺度, 乘以棱柱的“ 层” 数 。

播放段落

Three congruent pyramids fit inside the cube in #2, so the volume of each pyramid must be $\begin{array}{r}\frac{1}{3}\end{array}$ the volume of the cube. Therefore, the volume of a pyramid is $\begin{array}{r}\frac{A_{\text{base}}\cdot h}{3}\end{array}$ . Remember that pyramids with the same base area and height will have the same volume due to Cavalieri's principle, so both of the pyramids below will have a volume of $\begin{array}{r}\frac{A_{\text{base}}\cdot h}{3}\end{array}$ .
::立方体内三个相容的金字塔在 # 2, 所以每个金字塔的体积必须是立方体体积的13。 因此, 金字塔的体积是 Abaseh3. 记住, 由于卡瓦列里尼的原则, 基面积和高度相同的金字塔的体积是一样的, 因此下面的金字塔的体积都将是 Abaseh3 。

播放段落

Note: This is an informal argument for the formula for the volume of a pyramid. A rigorous derivation of the formula that considers pyramids of any base shape will be developed in calculus.
::注:这是对金字塔体积公式的非正式论证,将用微积分来严格推算考虑到任何基本形状的金字塔的公式。

---

播放段落

Examples
::实例实例实例实例

播放段落

Example 1
::例1

播放段落

The volume of a pyramid is given by $\begin{array}{r}{V}_{\text{pyramid}}=\frac{A_{\text{base}}\cdot h}{3}\end{array}$ . How does this formula help you find the formula for the volume of a cone?
::金字塔的体积由 Vpyramid= ABase_h3 给出。 这个公式如何帮助您找到锥体体体积的公式 ?

播放段落

A cone is essentially a pyramid with a circular base . The volume of a pyramid is given by $\begin{array}{r}{V}_{\text{pyramid}}=\frac{A_{\text{base}}\cdot h}{3}\end{array}$ . Since the area of the base of a cone is $\begin{array}{r}\pi r^2\end{array}$ , the formula for the volume of a cone is $\begin{array}{r}{V}_{\text{cone}}=\frac{\pi r^{2}h}{3}\end{array}$ .
::圆锥形基本上是一个金字塔,圆形底座,金字塔的体积由Vpyramid=Abaseh3.由于锥形底部面积为°r2,圆锥体底部的公式为Vconer2h3。

播放段落

The base area of the pyramid below is $\begin{array}{r}40{\text{cm}}^2\end{array}$ . What is the volume of the pyramid?
::金字塔下面的底部面积是40厘米2, 金字塔的体积是多少?

播放段落

$\begin{array}{r}{V}_{\text{pyramid}}=\frac{A_{\text{base}}\cdot h}{3}=\frac{(40)(6)}{3}=80{\text{cm}}^3\end{array}$
::Vpyramid=Abaseh3=(40)(6)3=80立方厘米

播放段落

Example 3
::例3

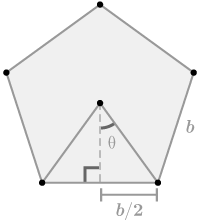
播放段落

Find the volume of a pyramid with a height of 10 inches and a regular pentagon base with an apothem of 1 inch.
::找到金字塔的体积,高度为10英寸,普通的五角形基地,诗歌为1英寸。

播放段落

$\begin{array}{r}{V}_{\text{pyramid}}=\frac{A_{\text{base}}\cdot h}{3}\end{array}$ . To find the area of the base, divide the pentagon into five congruent triangles . The apothem is the height of each of these triangles. Use trigonometry to find the base length of each of these triangles.
::Vpyramid=Abasih3. 要找到基点区域, 请将五角形分为五个相似的三角形。 方言是每个三角形的高度。 使用三角测量法查找每个三角形的基长 。

播放段落

Example 4
::例4

播放段落

Find the volume of a cone with a height of 10 inches and a radius of 1 inch.
::查找圆锥体的体积,高度为10英寸,半径为1英寸。

播放段落

$\begin{array}{rl}{V}_{\text{cone}}& =\frac{\pi r^{2}h}{3}\\ & =\frac{\pi (1{)}^2(10)}{3}\\ & =\frac{10\pi }{3}{\text{in}}^3\approx 10.47{\text{in}}^3\end{array}$
::Vconer2h3(1)(2)(10)3=103 英寸310.47英寸3

播放段落

CK-12 PLIX Interactive
::CK-12 PLIX 交互式互动

Summary

播放段落 A pyramid is a three-dimensional object with a base that is a polygon and triangular faces that meet at one vertex. ::金字塔是一个三维天体,基数是多边形和三角面,在一个顶端相交。 播放段落 The volume of a pyramid is $\begin{array}{r}V=\frac{\text{base}\times \text{height}}{3}\end{array}$   ::金字塔的体积是 V= basexh883 播放段落 A cone is a solid three-dimensional figure with a circular base and one vertex. The volume of a cone is $\begin{array}{r}V=\frac{\pi r^2\times h}{3}\end{array}$   ::锥体是一个具有圆形基和一个顶点的三维的固态图。锥体的体积是 Vr2xh3。

播放段落

1. Explain the connections between a prism and a pyramid. Why do you divide by three when calculating the volume of a pyramid?
::1. 解释棱晶和金字塔之间的联系。在计算金字塔的体积时,你为什么除以3?

播放段落

2. Explain the connections between a cone and a cylinder. Why do you divide by three when calculating the volume of a cone?
::2. 解释锥体与圆柱体之间的联系:计算锥体体体积时,为什么除以3?

播放段落

Find the volume of each solid based on its description. Keep your answers in terms of $\begin{array}{r}\pi \end{array}$  when applicable.
::根据每固体的描述查找每固体的体积。在适用的情况下,请保留您的回答 。

播放段落

3. A cone with a diameter of 4 inches and a height of 12 inches. 
::3. 直径为4英寸、高度为12英寸的锥形。

播放段落

4. A pyramid with a height of 15 inches and a regular hexagon base with an apothem of 4 inches. Round your answer to the nearest hundredths.
::4. 金字塔,高度15英寸,普通的六边形基座,假名4英寸。

播放段落

5. A cone with a radius of 8 centimeters and a height of 15 centimeters.
::5. 半径为8厘米、高度为15厘米的锥形。

播放段落

6. A square based pyramid such that the slant height of the pyramid is 10 inches and each triangular face has a base of 12 inches.
::6. 以方形为基础的金字塔,金字塔的倾斜高度为10英寸,每张三角脸的底部为12英寸。

播放段落

An hourglass is created by placing two congruent cones inside of a cylinder with the same base area. The radius is 5 inches and the height of the cylinder is 20 inches.
::将两个相容的圆锥体放在一个圆柱体内,以同一基点区域为基点,从而形成一个沙漏。半径为5英寸,圆柱体的高度为20英寸。

播放段落

7. Find the volume of one of the cones.
::7. 找出锥体之一的体积。

播放段落

8. Find the volume of the cylinder.
::8. 找到气瓶的体积。

播放段落

9. Find the volume of the space between the cones and the cylinder.
::9. 找出锥体与圆柱体之间的空间体积。

播放段落

10. You want to fill one of the cones with a thick liquid. If one cup of liquid has a volume of approximately $\begin{array}{r}14.44{\text{in}}^3\end{array}$ , how much liquid will you need to fill one of the cones? Round your answer to the nearest hundredths place.
::10. 要用厚液填充锥体之一,如果一杯液体的体积约为14.44英寸3,需要多少液体来填充锥体之一?

播放段落

11. A cone and a square pyramid have the same volume and height. The volume of each solid is $\begin{array}{r}100{\text{cm}}^3\end{array}$ . If the radius of the cone is 2.82 centimeters, what is the length of a side of the base of the pyramid? Round your answer to the nearest hundredths place.
::11. 锥体和方形金字塔的体积和高度相同,每块固体的体积为100厘米,如果锥体半径为2.82厘米,则金字塔底部的一面长度为多少?将答案转至最近的一百个地方。

播放段落

12. The ratio of the area of the red circle to the area of the base is 1:9. If the height of the cone is 15 inches, what is the length of $\begin{array}{r}\overline{AB}\end{array}$ ?
::12. 红圆面积与基地面积的比率是1:9.,如果锥体高度为15英寸,AB的长度是多少?

播放段落

13. The height of the cone below is 10 inches. Find the length of $\begin{array}{r}\overline{AB}\end{array}$ .
::13. 下方锥体的高度为10英寸,查找AB的长度。

播放段落

14. A regular tetrahedron is a triangular pyramid with four congruent equilateral faces. If each of the triangular faces of the tetrahedron has a base length of $\begin{array}{r}3\sqrt{2}\end{array}$  and a height of $\begin{array}{r}3\sqrt{6},\end{array}$   what is the volume of the tetrahedron?
::14. 普通四面形是一个三角金字塔,有四个相近的等边面,如果四面形的三角面形的基长为32,高度为36,四面形的体积是多少?

播放段落

15. The length of each side of the triangular faces making up a tetrahedron is $\begin{array}{r}s\end{array}$ . What is the volume of the tetrahedron in terms of $\begin{array}{r}s\end{array}$ ?
::15. 构成四面形的三角面面部每一面的长度为秒。四面形的体积是多少?

播放段落

16. Imagine a mountain roughly in the shape of a cone. It has a base whose circumference is roughly 78 miles and a height of roughly 8,800 feet. Sketch the scenario. Find the volume in terms of $\begin{array}{r}\pi .\end{array}$
::16. 想象一下大约为锥形的山,山底环绕约78英里,高度约8,800英尺。

播放段落

17. The Great Pyramid of Giza has a height of roughly 756 feet, and a square base with a side length of roughly 455 feet. What is the volume of the Great Pyramid? 
::17. 吉萨大金字塔的高度约为756英尺,一个长约455英尺的平方基,大金字塔的体积是多少?

播放段落

Review (Answers)
::审查(答复)

播放段落

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。