球球面

播放段落

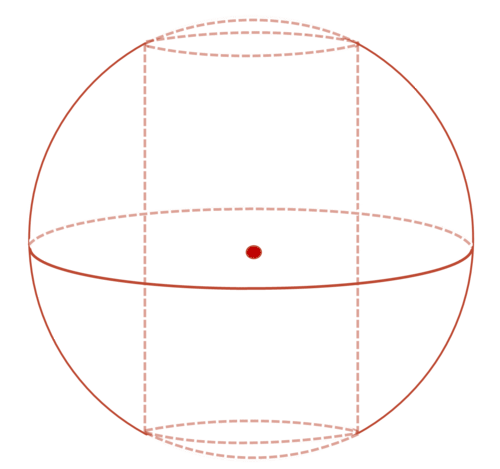
Sphere is the set of all points in three-dimensional space lying at the same distance (the radius ) from a given point (the center ), or the result of rotating a circle about one of its diameters .
::球体是三维空间内所有点的一组点,位于一个特定点(中心)的同一距离(半径),或旋转一个圆圈,环绕其直径之一的结果。

播放段落

There are two types of circles that can be drawn on the surface of a sphere. A great circle is the largest circle that can be drawn on the surface of a sphere, as the center of the great circle is also the center of the sphere. A small circle does not have its center at the center of the sphere. The radius of a small circle will be less than the radius of the sphere.
::在球体表面可以画出两种圆圈。大圆圈是球体表面可以画出的最大圆圈,因为大圆圈的中心也是球体的中心。小圆圈的中心不是球体的中心。小圆圈的半径将小于球体的半径。

播放段落

The components and properties of a sphere are analogous to those of a circle.
::球体的构件和特性与圆形的构件和特性相似。

播放段落

You have seen the formula for the of a sphere, cylinder and cone before.
::你以前见过球体、圆柱和锥形的公式。

播放段落

$\begin{array}{rl}{V}_{\text{sphere}}& =\frac{4}{3}\pi r^3\\ V_{\text{cone}}& =\frac{1}{3}\pi r^{2}h\\ V_{\text{cylinder}}& =\pi r^{2}h\end{array}$
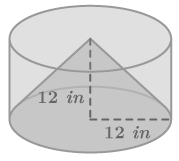
::Vsphere = 43r3Vcone = 13r2hVcylinderr2h

播放段落

The key to understanding the formula for the volume of a sphere is to compare a sphere inside of a cylinder with radius $\begin{array}{r}r\end{array}$ and height $\begin{array}{r}2r\end{array}$ with a double cone inside of a cylinder with radius $\begin{array}{r}r\end{array}$ and height $\begin{array}{r}2r\end{array}$ .
::理解球体体积公式的关键是将圆柱体内的球体与圆柱体半径r和高度2r与圆柱体内的双锥体R和高度2r作比较。

播放段落

The volume of the cylinder is : $\begin{array}{r}\pi r^{2}h=\pi r^2(2r)=2\pi r^3\end{array}$
::气瓶的体积为:°r2hr2(2r)=2r3

播放段落

The volume of the sphere is : $\begin{array}{r}\frac{4}{3}\pi r^3\end{array}$
::球体的体积是: 43°r3

播放段落

The volume of the cone is : $\begin{array}{r}\frac{1}{3}\pi r^{2}h=\frac{1}{3}\pi r^2(r)=\frac{1}{3}\pi r^3\end{array}$
::锥体的体积为: 13°r2h=13°r2(r)=13°r3

播放段落

The volume of the double cone is : $\begin{array}{r}2\cdot \frac{1}{3}\pi r^{2}h=2\cdot \frac{1}{3}\pi r^2(r)=\frac{2}{3}\pi r^3\end{array}$
::双锥体的体积为: 213r2h=2132(r)=23r3

播放段落

Volume of the space between the cylinder and the double cone = Volume of cylinder - Volume of double cone
::圆柱体与双锥体之间空间的体积 = 圆锥体的体积 - 双锥体的体积

播放段落

$\begin{array}{rl}& =2\pi r^3-\frac{2}{3}\pi r^3\\ & =\frac{(6-2)}{3}\pi r^3=\frac{4}{3}\pi r^3\end{array}$
::=2°r3-23°r3=(6-2)3°r3=43°r3

播放段落

The volume of the sphere is the same as the volume of the space between the cylinder and the double cone.
::球体的体积与圆柱体和双锥体之间的空间体积相同。

---

播放段落

Finding Area
::寻找地区

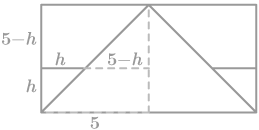
播放段落

Consider half of the double cone inside the cylinder and half the sphere (a hemisphere). If the radius of the sphere is 5 inches, label all the dimensions that you can. What is the area of the top surface of the hemisphere? What is the area of the top of the cylinder?
::考虑气瓶内半个双锥体和球体( 半球) 的一半。 如果球体半径为 5 英寸, 请标出您能够标出的所有尺寸。 半球顶部表面的面积是多少? 气瓶顶部的面积是多少?

播放段落

The area of the top of the cylinder is the same as the area of the top of the hemisphere . In each case the area is $\begin{array}{r}\pi r^2=\pi (5{)}^2=25\pi {\text{in}}^2\end{array}$ .
::圆柱体顶部的面积与半球顶部的面积相同,在每种情况下,面积为°r2(5)2=25英寸。

---

播放段落

Labeling Dimensions
::标签尺寸

播放段落

Imagine a slice is made at height $\begin{array}{r}h\end{array}$ . Draw the horizontal and vertical cross sections of each and label all dimensions in terms of $\begin{array}{r}h\end{array}$ .
::想象一个切片在高度 h 下制成。 绘制每个水平和垂直交叉段, 并用 h 标出所有维度 。

播放段落

First consider the vertical cross section through the center of the cone in the cylinder. Note that because the height and the radius of the cone are each 5 inches, isosceles right triangles are formed. Next consider the vertical cross section through the center of the sphere.
::首先考虑圆柱锥体中央的垂直交叉区域。 请注意, 由于锥体的高度和半径为每5英寸, 右三角形会形成等分形。 下一步考虑球体中央的垂直交叉区域 。

播放段落

Vertical Cross Section of Cone in Cylinder
::圆柱体内锥体垂直交叉部分

播放段落

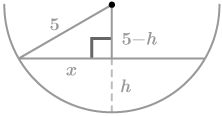
Vertical Cross Section of Sphere
::球体垂直交叉部分

播放段落

 The radius of the circular horizontal cross section is  $\begin{array}{r}x\end{array}$ . You can find the length of  $\begin{array}{r}x\end{array}$  by using the Pythagorean Theorem :  

::圆形水平截面的半径为 x。 您可以使用 Pytagoren 理论找到 x 的长度 :

播放段落

$\begin{array}{rl}{x}^2+(5-h{)}^2& =5^2\\ x^2+25-10h+h^2& =25\\ x& =\sqrt{10h-h^2}\end{array}$
::x2+(5-h)2=52x2+25-10h+h2=25x10-h2

播放段落

Now you can consider the horizontal cross sections.
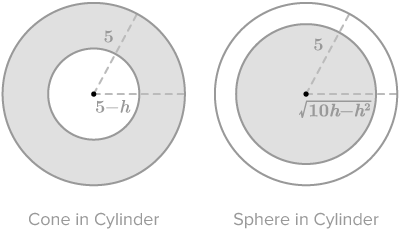
::现在您可以考虑横向横截段。

播放段落

                     Horizontal Cross Sections
::横向交叉区域

播放段落

Note that the shaded areas are the cross sections of the solids you are interested in. You are looking for the volume of the space between the cylinder and the cone and the volume of the sphere.
::请注意, 阴影区域是您感兴趣的固体的交叉部分。 您正在寻找圆柱体和锥体之间的空间体积以及球体的体积 。

---

播放段落

Drawing Conclusions
::绘图结论

播放段落

Confirm that the area of each shaded region below is the same. What does this tell you about the volume of the space between the cylinder and the cone compared to the volume of the sphere?
::确认以下每个阴影区域的面积相同。 与球体的面积相比, 圆柱体和锥体之间的空间体积如何?

播放段落

                          Horizontal Cross Sections
::横向交叉区域

播放段落

The area of the shaded region on the left is:
::左边的阴暗区域是:

播放段落

$\begin{array}{rl}A& =(5{)}^2\pi -(5-h{)}^2\pi \\ & =25\pi -(25-10h+h^2)\pi \\ & =25\pi -25\pi +10h\pi -h^2\pi \\ & =10h\pi -h^2\pi \end{array}$
::A=5-2___________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

播放段落

The area of the shaded region on the right is:
::右边的阴暗区域是:

播放段落

$\begin{array}{rl}A& ={\left(\sqrt{10h-h^2}\right)}^2\pi \\ & =10h\pi -h^2\pi \end{array}$
::A=(10h-h2)210hh2

播放段落

The areas are the same. Because the two solids lie between parallel planes, have the same heights, and have equal cross sectional areas, their volumes must be the same.
::区域是相同的。 因为这两块固体位于平行平面之间, 身高相同, 跨区面积相同, 它们的体积必须相同 。

---

播放段落

Vertical and Horizontal Cross Section
::纵向和横向交叉科

播放段落

Click the small blue arrow next to the image below and then drag the orange dot to move the cross section plane up or down. Observe the vertical and horizontal cross sections of the two solids. 
::单击下方图像旁边的小蓝箭头,然后拖动橙色点,将横段平面向上或向下移动。观察两个固体的垂直和水平交叉部分。

---

播放段落

Examples
::实例实例实例实例

播放段落

Example 1
::例1

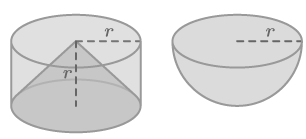
播放段落

It can be shown that the volume of the space between a cone and a cylinder with radius $\begin{array}{r}r\end{array}$ and height $\begin{array}{r}r\end{array}$ is the same as the volume of half a sphere (a hemisphere) with radius $\begin{array}{r}r\end{array}$ . Given this, what's the formula for the volume of a sphere?
::可以证明锥体与圆锥体之间的空间体积与半径(一个半球)和半径(r)的半球(一个半球)之间的空间体积相同。 有鉴于此,一个球体的体积的公式是什么?

播放段落

The volume of the cylinder is: $\begin{array}{r}\pi r^{2}h=\pi r^3\end{array}$
::气瓶的体积为: ir2hr3

播放段落

The volume of the cone is: $\begin{array}{r}\frac{\pi r^{2}h}{3}=\frac{\pi r^3}{3}\end{array}$
::锥体的体积为: r2h3r33

播放段落

Therefore, the volume of the space between the cone and the cylinder = Volume of cylinder - Volume of Cone
::因此,锥体与圆柱体之间的空间体积=圆柱体体体积-锥体体体积

播放段落

$\begin{array}{r}=\pi r^3-\frac{\pi r^3}{3}=\frac{(3-1)}{3}\pi r^3=\frac{2}{3}\pi r^3\end{array}$
::r3r33=(3-1)3r3=23r3

播放段落

If this is also the volume of a hemisphere, then the volume of a sphere must be twice as big. The volume of a sphere is:
::如果这也是一个半球的体积,那么一个球体的体积必须两倍于一个球体的体积。一个球体的体积是:

播放段落

$\begin{array}{r}\frac{2(2\pi r^3)}{3}=\frac{4\pi r^3}{3}\end{array}$
::2(2,2r3)3=4r33

播放段落

Find the volume of the space between the cylinder and the cone below.
::查找气瓶与锥体之间空间的体积。

播放段落

The volume of the cylinder is $\begin{array}{r}1728\pi {\text{in}}^3\end{array}$ and the volume of the cone is $\begin{array}{r}576\pi {\text{in}}^3\end{array}$ . The volume of the space between the cylinder and the cone is $\begin{array}{r}1152\pi {\text{in}}^3\end{array}$ .
::气瓶的体积为1728英寸3,锥体的体积为576英寸3,气瓶与锥体之间的空间体积为1152英寸3。

播放段落

Example 3
::例3

播放段落

Describe what portion of a sphere has the same volume as the volume calculated in Example #2.
::描述一个球体的哪个部分的体积与例2所计算的数量的体积相同。

播放段落

$\begin{array}{rl}1152& =\frac{2}{3}\pi r^3\\ r^3& =\frac{1152\cdot 3}{2}\\ r^3& =1728\\ r& =\sqrt[3]{1728}=12\text{in}\end{array}$
::1152=23r3r3=115232r3=1728r=1728r=1728r=12

播放段落

A hemisphere with radius 12 in would have the same volume.
::半径为12英寸的方半球的体积将相同。

播放段落

Example 4
::例4

播放段落

Find the volume of a sphere with a diameter of 15 cm .
::查找直径为15厘米的球体的体积。

播放段落

$\begin{array}{r}V=\frac{4\pi (7.5{)}^3}{3}=562.5\pi {\text{cm}}^3\end{array}$
::V=4(7.5)33=562.5cm3

播放段落

CK-12 PLIX Interactive
::CK-12 PLIX 交互式互动

Summary

播放段落 A sphere is a round, three-dimensional solid. All points on the surface of a sphere are equidistant from the center of the sphere. ::一个球体是一个圆形的,三维的固体。球体表面的所有点与球体中心的位置相等。 播放段落 The volume of a sphere is $\begin{array}{r}V=\frac{4}{3}\pi r^3\end{array}$   ::球体的体积是 V=43°r3 播放段落 A hemisphere is half a sphere. ::一个半球是半个领域。

播放段落

1. Find the volume of a sphere with a radius of 3 inches.
::1. 查找半径为3英寸的球体体积。

播放段落

2. Find the volume of a sphere with a diameter of 12 inches.
::2. 查找直径为12英寸的球体体积。

播放段落

3. Find the volume of a sphere with a diameter of 8 inches.
::3. 查找直径为8英寸的球体体积。

播放段落

4. In your own words, explain how the formula for the volume of a sphere is related to the volume of a double cone within a cylinder?
::4. 用你自己的话说,请解释一个球体体体积的公式与圆筒内双锥体体体积有何关系?

播放段落

A bead is created from a sphere by drilling a cylinder through the sphere. The original sphere has a radius of 8 mm. The cylinder drilled through the center has a radius of 4 mm.
::从球体中钻入圆柱,从球体中产生珠子。最初的球体半径为8毫米。通过中心钻入的圆柱子半径为4毫米。

播放段落

5. The original height of the sphere was 8 mm. After the cylinder is cut out from the sphere, what is the height of the bead? (Hint: Draw a right triangle and use the Pythagorean Theorem.)
::5. 球体最初的高度为8毫米,气瓶从球体中切除后,珠峰的高度是多少? (提示:绘制一个右三角形,并使用毕达哥伦理论。 )

播放段落

6. What is the volume of the original sphere? What is the volume of the cylinder?
::6. 最初球体的体积是多少?圆柱体的体积是多少?

播放段落

A cylindrical container holds three tennis balls. The diameter of the cylinder is 4 inches, which is approximately the same as the diameter of each tennis ball. The height of the cylinder is 12 inches.
::圆柱形容器有三个网球,圆柱体直径为4英寸,与每个网球直径大致相同,圆柱体高度为12英寸。

播放段落

7. What is the volume of one tennis ball?
::7. 一个网球的体积是多少?

播放段落

8. What is the volume of the space between the tennis balls and the cylinder?
::8. 网球和圆柱之间的空间有多大?

播放段落

9. If one cup of water has a volume of approximately  $\begin{array}{r}14.44{\text{in}}^3\end{array}$ , how many cups of water would fit in the cylinder with the tennis balls? Round your answer to the nearest hundredths place.
::9. 如果每杯水的体积大约为14.44英寸,每杯约14.44英寸,有多少杯水装在圆筒里,装有网球?

播放段落

Think of a sphere of radius $\begin{array}{r}r\end{array}$ as being made up of a large number $\begin{array}{r}k\end{array}$ of congruent small square based pyramids. Let the area of each square base be $\begin{array}{r}B\end{array}$ .
::将半径范围想象成由千克相近的小平方金字塔构成。 让每一平方基的面积为 B 。

播放段落

10. The diameter of the Earth is approximately 7,917.5 miles and the diameter of the Moon is about 2,159 miles. What is the Moon's volume compared to the Earth's volume as a percentage.
::10. 地球直径约为7,917.5英里,月球直径约为2,159英里,与地球体积的百分比相比,月球体积是多少。

播放段落

11. If the diameter of the moon doubled, how would its volume change? Explain.
::11. 如果月球直径翻番,其体积会如何变化?

播放段落

Review (Answers)
::审查(答复)

播放段落

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。