两维和三维之间的连接

播放段落

Recall that a cross section is the shape you see when you make one slice through a solid. A solid can have many different cross sections depending on where you make the slice. Consider a hexagonal pyramid . Cross sections perpendicular to the base will be triangles. Cross sections parallel to the base will be hexagons. It is also possible to take cross sections using planes that are neither parallel nor perpendicular to the base. Below, a hexagonal pyramid has been sliced at a slant . The cross section is a hexagon .
::提醒您注意, 跨区是您在用固体切片时看到的形状。 固态可以拥有许多不同的跨区, 取决于您在哪里切片。 考虑一个六边形金字塔。 与基底垂直的跨区将是三角形。 与基底平行的跨区将是六边形。 使用既不平行也不与基底垂直的飞机也可以跨区。 下面, 六边形金字塔已被倾斜切开。 横段是六边形 。

播放段落

Cross sections are one way that two dimensional objects are connected to three dimensional objects.
::两维天体连接到三维天体的 交叉区域是同一种方式。

播放段落

A second connection between two and three dimensions comes from the fact that three dimensional solids can be created by rotating two dimensional objects around a line .
::两维和三维之间的第二个联系来自一个事实,即三维固体可以通过在一条线上旋转两维物体而产生。

播放段落

Rotating 2D shapes in 3D
::3D 中旋转 2D 形状

播放段落

Click the small blue arrow next to the image below and select a 2D shape given below. Observe how this 2D shape defines a 3D object on being rotated. 
::单击下面图像旁边的小蓝箭头,然后选择下面给定的 2D 形状。观察这个 2D 形状在旋转时如何定义 3D 对象 。

播放段落

Identify the solid that is created when the following rectangle is rotated around the line.
::识别以下矩形围绕线旋转时产生的固体。

播放段落

Answer: The solid is
::回答:固体是

播放段落

Let's look at some problems about cross sections.
::让我们来研究一下关于交叉部分的一些问题。

播放段落

1. Identify the solid that is created when the following shape is rotated around the line.
::1. 标明以下形状围绕线旋转时产生的固体。

播放段落

The solid is a cone with radius 5 cm.
::固体是半径为5厘米的锥体。

播放段落

2. Find the of the solid from #1 .
::2. 从#1找到固体的固体。

播放段落

The volume of a cone is $\begin{array}{r}{V}_{\text{cone}}=\frac{\pi r^{2}h}{3}\end{array}$ . The radius is 5 cm . To find the height of the cone, use the Pythagorean Theorem :
::锥体的体积是Vconer2h3. 半径为5厘米。 要找到锥体的高度, 请使用 Pytagoren 理论 :

播放段落

$\begin{array}{rl}{5}^2+h^2& =9^2\\ h^2& =9^2-5^2\\ h^2& =81-25=56\\ h& =\sqrt{56}\approx 7.48\text{cm}\end{array}$
::52+h2=92h2=92-52h2=81-25=56h=567.48厘米

播放段落

The volume of the cone is:
::锥体的体积是:

播放段落

$\begin{array}{r}{V}_{\text{cone}}=\frac{\pi (5{)}^2(7.48)}{3}\approx 195.83{\text{cm}}^3\end{array}$
::Vcone (5) 2(7.483) 195.83 立方厘米

播放段落

3. Identify at least three two dimensional shapes created by cross sections of the solid from the first problem.
::3. 确定至少三个两维的形状,这些形状由第一个问题产生的固体的交叉部分所产生。

播放段落

Cross sections taken parallel to the base will be circles . Cross sections taken perpendicular to the base will be triangles . When the cross section is taken at a slant, there are many other possibilities. Three additional cross sections are an ellipse , a filled in parabola or a hyperbola .
::与基底平行的交叉区段将是圆形。 与基底垂直的交叉区段将是三角形。 当跨区段在倾斜时, 还有很多其他可能性。 另三个交叉区段是椭圆、 以抛物线或双曲线填充的。

播放段落

Examples
::实例实例实例实例

播放段落

Example 1
::例1

播放段落

The shaded figure below is rotated around the line. What is the volume of the solid that is created?
::下面的阴影图围绕线旋转。创建的固体的体积是多少?

播放段落

The resulting solid is a sphere with a sphere removed from the center .
::产生的固体是一个球体 球体从中心取出一个球体

播放段落

Volume of the resulting solid = Volume of the large sphere - Volume of the small sphere 
::所产生固体体积量=大球体量-小球体量

播放段落

Example 2
::例2

播放段落

Identify the solid that is created when the figure below is rotated around the line.
::标明下图围绕线旋转时产生的固体。

播放段落

The solid is a cylinder with a hemisphere on top. The radius of each is 4 cm.
::固体是一个圆柱体,上面有一个半球。每个圆柱体的半径为4厘米。

播放段落

Example 3
::例3

播放段落

Find the volume of the solid from Example #2.
::从例2中查找固体的体积。

播放段落

Example 4
::例4

播放段落

Identify at least three two dimensional shapes created by cross sections of the solid from Example #2.
::确定至少三个二维的形状, 由来自例2的固体的交叉区块所创建的两维形状。

播放段落

Possible answers: Cross sections taken parallel to the base will be circles. Cross sections taken perpendicular to the base will be with half circles on top. Some cross sections taken at a slant will be ellipses.
::可能的答案: 与基底平行的交叉部分是圆形的。 与基底垂直的交叉部分是上面的半圆形。 倾斜时的一些交叉部分是省略号 。

Summary

播放段落 A cross section is the intersection of a three-dimensional solid with a plane. Three dimensional solids can be created by rotating two dimensional objects around a line. ::横截面是三维固体与平面的交叉点。三维固体可以通过在一条线上旋转两维物体而产生。 播放段落 Cross sections of cones are called conics : circles, parabolas, ellipses, and hyperbolas. ::锥锥体的交叉部分被称为二次曲线:圆圈、parabolas、椭圆和双螺旋。

播放段落

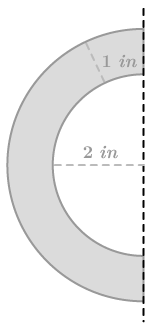
Use the picture below for #1-#3.
::使用下面的图片用于 # 1 - # 3 。

播放段落

1. Describe the solid that is created when the figure above is rotated around the line.
::1. 描述上图按线旋转时产生的固体。

播放段落

2. Find the volume of the solid.
::2. 寻找固体的体积。

播放段落

3. Identify at least 3 two dimensional shapes created by cross sections of the solid.
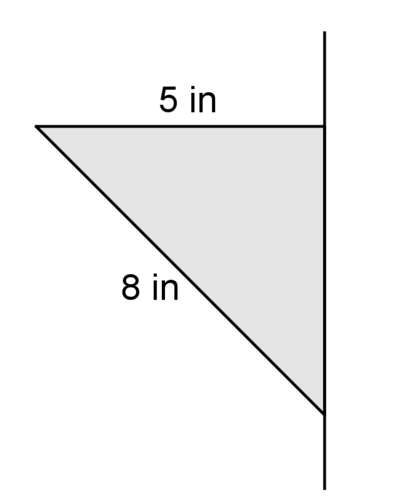
::3. 确定至少3个由固体交叉部分产生的2维形状。

播放段落

Use the picture below for #4-#6.
::使用下面的图片为 # 4 -# 6 提供图片 。

播放段落

4. Describe the solid that is created when the figure above is rotated around the line.
::4. 描述上图按线旋转时产生的固体。

播放段落

5. Find the volume of the solid.
::5. 寻找固体的体积。

播放段落

6. Identify at least 3 two dimensional shapes created by cross sections of the solid.
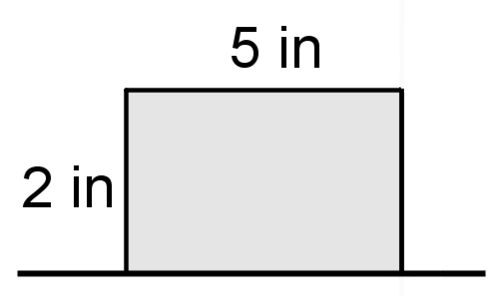
::6. 确定至少3个由固体交叉部分产生的2维形状。

播放段落

Use the picture below for #7-#9.
::使用下面的图片为 # 7- # 9 绘制 。

播放段落

7. Describe the solid that is created when the figure above is rotated around the line.
::7. 描述上图按线旋转时产生的固体。

播放段落

8. Find the volume of the solid.
::8. 寻找固体的体积。

播放段落

9. Identify at least 2 two dimensional shapes created by cross sections of the solid.
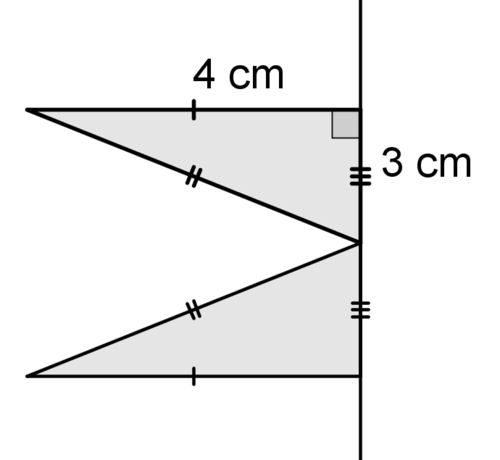
::9. 确定至少两维两维由固体交叉部分产生的形状。

播放段落

Use the picture below for #10-#12.
::用下面的图片显示 #10 -#12。

播放段落

10. Describe the solid that is created when the figure above is rotated around the line.
::10. 描述上图按线旋转时产生的固体。

播放段落

11. Find the volume of the solid.
::11. 寻找固体的体积。

播放段落

12. Identify at least 2 two dimensional shapes created by cross sections of the solid.
::12. 确定至少两个由固体交叉部分产生的两维形状。

播放段落

Use the picture below for #13-#15.
::使用下面的图片为 #13-#15。

播放段落

13. Describe the solid that is created when the figure above is rotated around the line.
::13. 描述上图按线旋转时产生的固体。

播放段落

14. Find the volume of the solid.
::14. 寻找固体的体积。

播放段落

15. Identify at least 2 two dimensional shapes created by cross sections of the solid.
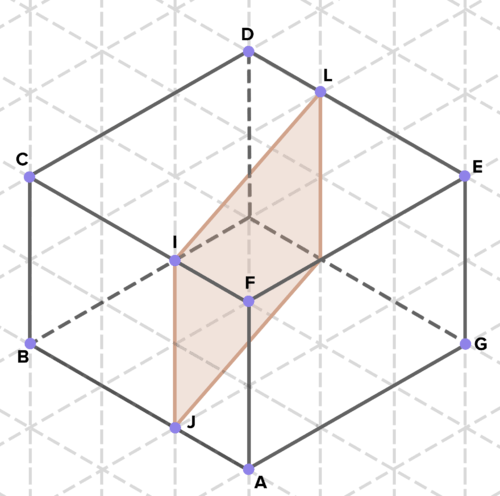
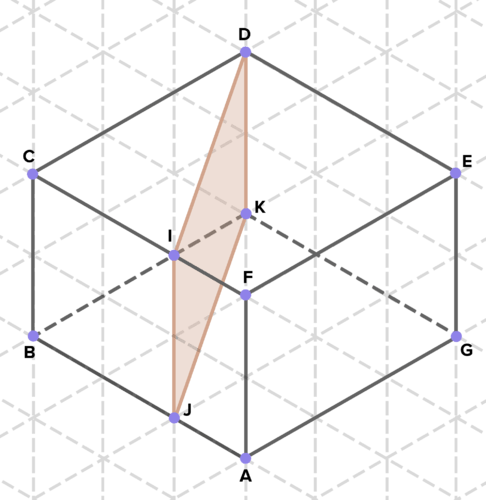
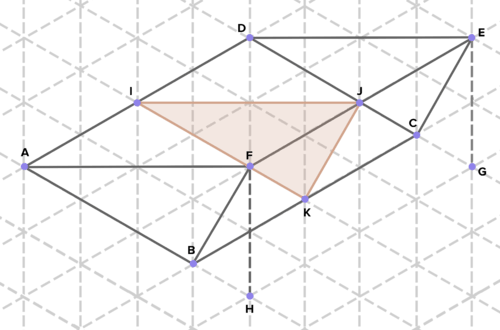
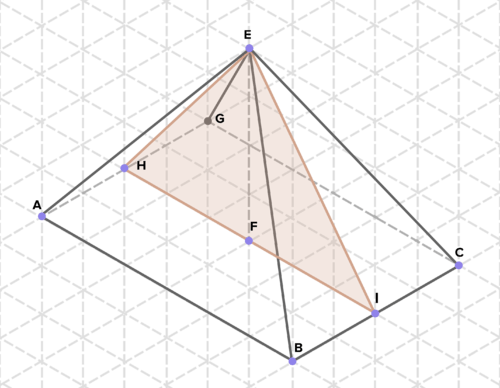
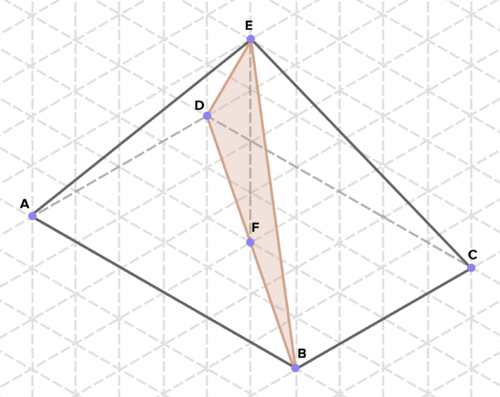
::15. 确定至少两个由固体交叉部分产生的两维形状。

播放段落

16. Below are cross-sections of various solids. Find the area of each cross-section. (On the isometric grid paper shown, a side of an equilateral triangle represents 1 unit of length in any direction.)
::16. 下面是各种固体的截面,查找每个截面的面积。 (在显示的等度网格纸上,等边三角形的一面代表任何方向的长度1单位。 )

播放段落

Review (Answers)
::审查(答复)

播放段落

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。