平行线和直直线的斜面

播放段落
1. They are parallel and so they never intersect.
   ::它们是平行的,所以它们从不交叉。
播放段落
2. They are perpendicular and so they intersect at a right angle .
   ::它们是垂直的,因此它们从一个正确的角度交叉。
播放段落
3. They intersect, but they are not perpendicular.
   ::它们相互交织,但并不垂直。

播放段落

The slope of a line is a measure of its steepness. For a line written in the form $\begin{align*}y=mx+b\end{align*}$ , " $\begin{align*}m\end{align*}$ " is the slope. Given two lines, their slopes can help you to determine whether the lines are parallel, perpendicular or neither.
::线的斜坡是线的陡度量。对于以 y=mx+b 格式写成的线,“m”是斜度。在两条线下,它们的斜坡可以帮助您确定线是平行的、垂直的还是两侧的。

播放段落

Let there be two lines $\begin{align*}l_1\end{align*}$ and $\begin{align*}l_2\end{align*}$ , which make angles $\begin{align*}\theta_1\end{align*}$ and $\begin{align*}\theta_2\end{align*}$ respectively with the positive direction of the $\begin{align*}x\end{align*}$ -axis.
::让两行 1 和 12 分别产生 + 1 和 + 2 角度, 以 x 轴向正向 。

播放段落

Then $\begin{align*}\theta_1 = \theta_2\end{align*}$ ( as $\begin{align*}l_1 \parallel l_2\end{align*}$ )
::然后是12 (作为l1l2)

播放段落

$\begin{align*}\therefore\end{align*}$ $\begin{align*}\tan \theta_1 = \tan \theta_2\end{align*}$
::1=2

播放段落

which shows that the slopes of the lines are equal. Hence if $\begin{align*}m_1\end{align*}$ and $\begin{align*}m_2\end{align*}$ are the slopes of the two parallel lines , then
::显示线条的斜度相等。因此,如果 m1 和 m2 是两条平行线的斜度,那么

播放段落

$\begin{align*}m_1 = m_2\end{align*}$
::m1=m2

播放段落

Thus, if two lines are parallel then they have the same slope.
::因此,如果两条线平行,那么两条线的斜坡相同。

播放段落

Let there be two lines $\begin{align*}l_1\end{align*}$ and $\begin{align*}l_2\end{align*}$ and $\begin{align*}m_1\end{align*}$ and $\begin{align*}m_2\end{align*}$ be their slopes. Let $\begin{align*}\theta_1\end{align*}$ and $\begin{align*}\theta_2\end{align*}$ be the inclination of these lines.
::让两行 1 和 12 以及 m1 和 m2 成为它们的斜坡。 让 + 和 % 2 成为这些线的倾角 。

播放段落

$\begin{align*}\theta_2 & = 90^\circ + \theta_1 \\ \tan \theta_2 & = \tan (90^\circ + \theta_1) \\ \tan \theta_2 & = - \cot \theta_1 \\ \tan \theta_2 & = - \frac{1}{\tan \theta_1}\\ m_2 & = - \frac{1}{m_1}\end{align*}$
::=2=901tan2=tan(901)tan2cot1tan21tan21tan}1tan11}1tan}1tan}1}1tan1m211}1m21m1

播放段落

Thus, two lines are perpendicular if and only if they have slopes that are opposite reciprocals. Another way of thinking about this is that the product of the slopes of perpendicular lines will always be -1. (Note that $\begin{align*}(m)\big(-\frac{1}{m}\big)=-\frac{m}{m}=-1\end{align*}$ ).
::因此,两条线是垂直的,只要它们有对等的斜坡。 另一种思考方式是,垂直的斜坡的产物始终是-1。 (注意(m)(-1m)mm1)

---

播放段落

Determining the Distinction Between Two Lines
::确定两线之间的区别

播放段落

Consider two lines $\begin{align*}y=ax+b \end{align*}$ and $\begin{align*}y=ax+c\end{align*}$ with $\begin{align*}b\ne c\end{align*}$ . Note that these two lines have the same slope, $\begin{align*}a\end{align*}$ .
::将两行 y= ax+b 和 y= ax+c 与 bc 相提并论。 请注意, 这两行的斜坡为 a 。

播放段落

You know that the two lines are distinct (not the same line) as they have different $\begin{align*}y\end{align*}$ - intercepts . The first line has a $\begin{align*}y\end{align*}$ -intercept at $\begin{align*}(0, b)\end{align*}$ and the second line has a $\begin{align*}y\end{align*}$ -intercept at $\begin{align*}(0,c)\end{align*}$ .
::您知道两条线是不同的( 不是同一行) , 因为它们有不同的 y 截取 。 第一行在 0, b) 处有一个 y 截取 , 第二行在 0, c) 处有一个 y 截取 。

播放段落

Algebraically you can find the point of intersection of the lines.
::代数中,您可以找到线条的交叉点。

播放段落

You can use substitution to attempt to find the point of intersection.
::您可以使用替代来尝试找到交叉点 。

播放段落

$\begin{align*}y=ax+b\end{align*}$ and $\begin{align*}y=ax+c\end{align*}$
::y=ax+b和y=ax+c y=ax+b和y=ax+c

播放段落

Therefore:
::因此:

播放段落

$\begin{align*}ax+b &=ax+c \\ b &= c\end{align*}$
::ax+b=轴+cb=c

播放段落

This is a contradiction because it was stated that $\begin{align*}b \ne c\end{align*}$ . Therefore, these two lines do not have a point of intersection. This means the lines must be parallel. This proves that if two lines have the same slope, then they are parallel.
::这是自相矛盾的, 因为上面写着 bc。 因此, 这两条线没有交叉点 。 这意味着两条线必须是平行的 。 这证明如果两条线有相同的斜度, 那么两条线是平行的 。

播放段落

Consider rectangle $\begin{align*}ABCD\end{align*}$ with $\begin{align*}BC=m\end{align*}$ , $\begin{align*}EC=1\end{align*}$ and perpendicular lines $\begin{align*}\overleftrightarrow{AE}\end{align*}$ and $\begin{align*}\overleftrightarrow{BE}\end{align*}$ . Because it is a rectangle, $\begin{align*}AD=BC\end{align*}$ $\begin{align*}=m\end{align*}$ . The two triangles are similar because they have congruent angles. Let $\begin{align*}\angle BEC = \theta\end{align*}$ , then $\begin{align*}\angle EBC = 90 - \theta\end{align*}$ . Similarly, $\begin{align*}\angle AED = 90 - \theta\end{align*}$ , then $\begin{align*}\angle DAE = \theta\end{align*}$ .
::考虑以 BC=m、 EC=1 和 AE 和 BE 的垂直直线矩形ABCD。 因为它是一个矩形, AD= BC=m。 这两个三角形相似, 因为它们具有相近角度 。 让 {BEC\\, 然后 EBC=90\\ 。 类似地, AED=90\ , 然后DAE\\ 。

播放段落

You can see that each of the three triangles in the picture have the same angle measures , so they must all be similar. In particular, $\begin{align*}\triangle ADE\end{align*}$ is similar to $\begin{align*}\triangle ECB\end{align*}$ , by $\begin{align*}AA \sim\end{align*}$ .
::您可以看到图片中的三个三角形中每个三角形都有相同的角度度量, 因此它们必须都相似。 特别是, QADE 与 AAQ 的 QECB 类似 。

播放段落

Now, use the fact that $\begin{align*}\triangle ADE\end{align*}$ is similar to $\begin{align*}\triangle ECB\end{align*}$ to find the length of $\begin{align*}DE\end{align*}$ . Then, find the slopes of lines $\begin{align*}\overleftrightarrow{AE}\end{align*}$ and $\begin{align*}\overleftrightarrow{BE}\end{align*}$ and show that their product is -1.
::现在,使用“QAADE”与“ECB”相似的事实来找到DE的长度。然后,找到“AE”和“BE”线的斜坡,并显示其产品是-1。

播放段落

Because $\begin{align*}\triangle ADE\end{align*}$ is similar to $\begin{align*}\triangle ECB\end{align*}$ , the following proportion is true:
::由于“ADE”与“EECB”相似,以下比例是真实的:

播放段落

$\begin{align*}\frac{BC}{EC} & = \frac{DE}{AD} \\ \frac{m}{1}& =\frac{DE}{m}\end{align*}$
::BCEC = DEADm1 =DEm

播放段落

Solving this proportion you have that $\begin{align*}DE=m^2.\end{align*}$
::正在解决您拥有的 DE=m2 的比例 。

播放段落

The slopes of the lines can be found using $\begin{align*}\frac{\text{rise}}{\text{run}}\end{align*}$ . The slope of line $\begin{align*}\overleftrightarrow{AE}\end{align*}$ is $\begin{align*}-\frac{m}{m^2}=-\frac{1}{m}\end{align*}$ and the slope of $\begin{align*}\overleftrightarrow{BE}\end{align*}$ is $\begin{align*}\frac{m}{1}=m\end{align*}$ .
::线条的斜坡可使用斜坡找到。 AE 线的斜坡为- mm21m, BE 的斜坡为m1=m。

播放段落

The product of the slopes is $\begin{align*}\Big(-\frac{1}{m}\Big)(m)=-\frac{m}{m}=-1\end{align*}$ .
::斜坡的产物是 (-1m(m) ) 1 。

播放段落

This proves that if two lines are perpendicular, then their slopes will be opposite reciprocals (the product of the slopes will be -1).
::这证明,如果两条线是垂直的,那么它们的斜坡将是对等的(斜坡的产物将是-1)。

---

播放段落

Examples
::实例实例实例实例

播放段落

Example 1
::例1

播放段落

Find the equation of the line parallel to $\begin{align*}y=2x - 4\end{align*}$ that passes through the point $\begin{align*}(2,-3)\end{align*}$ . Then, find the equation of the line perpendicular to $\begin{align*}y = 2x -4\end{align*}$ that passes through the point $\begin{align*}(2,-3)\end{align*}$ . How are the two lines that you found related?
::查找与y=2x-4平行的直线的方程式,该直线穿过点(2, - 3),然后找到与y=2x-4垂直的直线的方程式,该直线穿过点(2, - 3),您发现的两个直线关系如何?

播放段落

To find the equation of the line parallel to $\begin{align*}y=2x-4\end{align*}$ that passes through the point $\begin{align*}(2, -3)\end{align*}$ , remember that parallel lines must have equal slopes. This means that the new line must have a slope of $\begin{align*}2\end{align*}$ and pass through the point $\begin{align*}(2,-3)\end{align*}$ . All you need to do is solve for the $\begin{align*}y\end{align*}$ -intercept.
::要找到与y=2x-4平行的线线的方程式, 穿过点(2, - 3) , 请记住平行线必须具有相等的斜度。 这意味着新线必须有一个 2 的斜度, 并通过点 (2, - 3) 。 您需要做的就是解决 y 界面问题 。

播放段落

$\begin{align*}-3 &=2(2)+b\\ -3 &=4+b\\ b &=-7\\\end{align*}$
::- 3=2(2)+b-3=4+bb7

播放段落

The equation of the line is $\begin{align*}y=2x-7\end{align*}$ .
::线的方程式是 y=2x-7。

播放段落

To find the equation of the line perpendicular to $\begin{align*}y=2x-4\end{align*}$ that passes through the point $\begin{align*}(2,-3)\end{align*}$ , remember that perpendicular lines will have opposite reciprocal slopes. This means that the new line must have a slope of $\begin{align*}-\frac{1}{2}\end{align*}$ and pass through the point $\begin{align*}(2,-3)\end{align*}$ . Again, all you need to do is solve for the $\begin{align*}y\end{align*}$ -intercept.
::要找到横穿点(2,-3)的与y=2x-4垂直的线的方程,请记住,垂直的线将具有对等的斜坡。这意味着新线必须有一个 - 12 的斜坡,然后穿过点(2,-3) 。再次,你需要做的就是解决Y 的插口问题。

播放段落

$\begin{align*}-3 &=-\frac{1}{2}(2)+b\\ -3 &=-1+b\\ -4 &=b\end{align*}$
::- 312(2)+b-31+b-4=b

播放段落

The equation of the line is $\begin{align*}y=-\frac{1}{2}x-4\end{align*}$ .
::线的方程式是y12x-4。

播放段落

The two lines that were found $\begin{align*}\bigg( y=2x-7 \big .\end{align*}$ and $\begin{align*}y = \left . -\frac{1}{2}x-4 \right )\end{align*}$ are also perpendicular. Note that they have opposite reciprocal slopes.
::找到的两条线(y=2x-7和y=12x-4)也是垂直的。请注意,两条线的对等斜坡对齐。

播放段落

Consider two parallel lines $\begin{align*}y=ax+b\end{align*}$ and $\begin{align*}y=cx+d\end{align*}$ with $\begin{align*}b\ne d\end{align*}$ . Show that $\begin{align*}a=c\end{align*}$ .
::将两个平行行 y= ax+b 和 y= cx+d 与 bd 一同考虑。 请显示 a= c 。

播放段落

Suppose $\begin{align*}a\ne c\end{align*}$ . You can solve a system of equations to find the point of intersection of the two lines.
::ac. 您可以解开一个方程系统 找到两条线的交叉点 。

播放段落

$\begin{align*}y=ax+b\end{align*}$ and $\begin{align*}y=cx+d\end{align*}$
::y=ax+b和y=cx+d y=ax+b和y=cx+d

播放段落

Therefore:
::因此:

播放段落

$\begin{align*}ax+b &=cx+d\\ x(a-c) &=d-b\\ x &=\frac{d-b}{a-c}\end{align*}$
::ax+b=cx+dx(a-c)=d-bx=d-ba-c

播放段落

If $\begin{align*}a\ne c\end{align*}$ , then this point exists so the lines intersect. This is a contradiction because it was stated that the lines were parallel. Therefore, $\begin{align*}a\end{align*}$ must be equal to $\begin{align*}c\end{align*}$ . This proves that if two lines are parallel then they must have the same slope.
::如果 ac, 则此点存在, 线条会相互交叉。 这是矛盾的, 因为上面写到线条是平行的。 因此, 一个必须等于 c。 这证明, 如果两条线是平行的, 那么两条线必须具有相同的斜坡 。

播放段落

Example 3
::例3

播放段落

Consider two lines intersecting at the origin as shown below. Find the lengths of the legs of each triangle . Then, show that $\begin{align*}\triangle BCO\end{align*}$ is similar to $\begin{align*}\triangle ODA\end{align*}$ .
::考虑下方来源处的两条线交叉。 查找每个三角形的腿长度。 然后, 显示 QBCO 与 QODA 相似 。

播放段落

The lengths of the legs of the triangles are shown below.
::三角形腿的长度如下所示。

播放段落

$\begin{align*}\triangle BCO\sim \triangle ODA\end{align*}$ with a ratio of $\begin{align*}m:1\end{align*}$ by $\begin{align*}SAS \sim\end{align*}$ .
::按SAS=1的比例计算,BCO+ODA为m:1。

播放段落

$\begin{align*}\frac{BC}{OD}\end{align*}$ $\begin{align*}= \frac{m}{1}\end{align*}$ and $\begin{align*}\frac{CO}{DA}\end{align*}$ $\begin{align*}=\frac{1}{\frac{1}{m}}=\frac{m}{1}.\end{align*}$
::BCOD=m1,COD=11m=m1。

播放段落

Also $\begin{align*}\angle C\cong\angle D\end{align*}$ .
::也是CD

播放段落

Example 4
::例4

播放段落

Using the picture from Example #3, find the slopes of lines $\begin{align*}\overleftrightarrow{AO}\end{align*}$ and $\begin{align*}\overleftrightarrow{BO}\end{align*}$ and verify that their product is -1. Then use the fact that $\begin{align*}\triangle BCO\end{align*}$ is similar to $\begin{align*}\triangle ODA\end{align*}$ to show that $\begin{align*}\overleftrightarrow{AO}\end{align*}$ and $\begin{align*}\overleftrightarrow{BO}\end{align*}$ must be perpendicular.
::使用 例3 中的图片, 找到 AO 和 BO 线的斜坡, 并验证它们的产品是-1。 然后使用 BCO 与 ODA 相似这一事实来显示 AO 和 BO 必须是垂直的 。

播放段落

The slope of line $\begin{align*}\overleftrightarrow{AO}\end{align*}$ is $\begin{align*}-\frac{1}{m}\end{align*}$ and the slope of $\begin{align*}\overleftrightarrow{BO}\end{align*}$ is $\begin{align*}\frac{m}{1}\end{align*}$ . The product of the slopes is $\begin{align*}\Big(-\frac{1}{m}\Big)(m)=-\frac{m}{m}=-1\end{align*}$ .
::AO线的斜坡为-1米,BO的斜坡为m1。 斜坡的产物为(-1米(m))毫米(mm)1。

播放段落

Because $\begin{align*}\triangle BCO\end{align*}$ is similar to $\begin{align*}\triangle ODA\end{align*}$ , their corresponding angles must be congruent. This means that:
::由于“BCO”与“ODA”相似,它们相应的角度必须一致。 这意味着:

播放段落
• $\begin{align*}m\angle OCB\end{align*}$ $\begin{align*}=\end{align*}$ $\begin{align*}m \angle ADO\end{align*}$
  ::mOCB=mADO
播放段落
• $\begin{align*}m\angle BOC\end{align*}$ $\begin{align*}=\end{align*}$ $\begin{align*}m \angle DAO\end{align*}$
  ::MZBOC=mDAO BOC=mDAO BOC=mDAO BOC=mDAO BOC=mDAO

播放段落

Also, because they are right triangles :
::而且,因为它们是正确的三角形:

播放段落
• $\begin{align*}m\angle OBC +m\angle BOC=90^\circ\end{align*}$
  ::MOBC+MBOC=90
播放段落
• $\begin{align*}m\angle DOA+m\angle DAO=90^\circ\end{align*}$
  ::mDOA+mDAO=90

播放段落

By substitution, $\begin{align*}m\angle DOA+m\angle BOC=90^\circ \end{align*}$ . Because $\begin{align*}\angle DOA\end{align*}$ , $\begin{align*}\angle BOC\end{align*}$ and $\begin{align*}\angle AOB\end{align*}$ form a straight line , the sum of their measures must be $\begin{align*}180^\circ \end{align*}$ . Therefore, $\begin{align*}m\angle AOB\end{align*}$ must be $\begin{align*}90^\circ \end{align*}$ .
::由于“DOA”、“ZBOC”和“AOB”构成一条直线,它们的措施总和必须是180。因此,“MZAOB”必须是90。

播放段落

Because $\begin{align*}m \angle AOB=90^\circ\end{align*}$ , $\begin{align*}\overleftrightarrow{AO}\end{align*}$ and $\begin{align*}\overleftrightarrow{BO}\end{align*}$ must be perpendicular . This proves that if two lines have opposite reciprocal slopes, then they are perpendicular.
::因为 mAOB=90, AO 和 BO 必须是垂直的。 这证明如果两条线的对等斜坡是对的, 那么它们就是垂直的 。

播放段落

CK-12 PLIX: Equations of Parallel and Perpendicular Lines
::CK-12-PLIX: 平行线和直直线等同

Summary

播放段落 Two or more lines are parallel when they lie in the same plane and never intersect. These lines will always have the same slope. ::两条或多条线在同平面上是平行的,而从不交叉。这些线将永远具有相同的斜坡。 播放段落 Two lines that are perpendicular will intersect at a 90o or right, angle. The slopes of perpendicular lines are opposite reciprocals of each other. ::两条垂直直线将在90o或右边角交叉。垂直直线的斜坡是对等的。 播放段落 A point of intersection is the point where two intersecting lines meet. This will be a point that satisfies both equations. ::交叉点是两条交叉线相交点。 这将满足两个方程式的点 。

播放段落

1. Describe the three ways that two lines could interact.
::1. 说明两条线可以互动的三种方式。

播放段落

2. What does it mean for two lines to be parallel? How are the slopes of parallel lines related?
::2. 两条线平行意味着什么?平行线的斜坡如何相关?

播放段落

3. What does it mean for two lines to be perpendicular? How are the slopes of perpendicular lines related?
::3. 两条直线是否垂直意味着什么?垂直线的斜坡如何相关?

播放段落

4. Use algebra to show why the lines $\begin{align*}y=3x-4\end{align*}$ and $\begin{align*}y=3x+7\end{align*}$ (lines with the same slope) must be parallel.
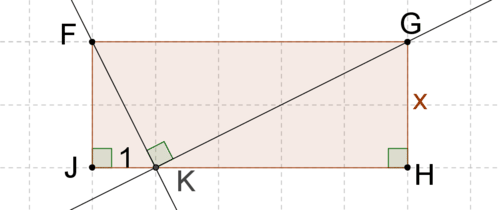
::4. 使用代数来显示为什么线y=3x-4和y=3x+7(同一坡度的线)必须平行。

播放段落

5. Use the method from Example B and Example C to show why the slopes of lines $\begin{align*}\overleftrightarrow{FK}\end{align*}$ and $\begin{align*}\overleftrightarrow{KG}\end{align*}$ must be opposite reciprocals. Assume that $\begin{align*}FGHJ\end{align*}$ is a rectangle.
::5. 使用例B和例C的方法来说明为什么 " QFK " 和 " QKG " 线的斜坡必须是对等的,假设FGHJ是一个矩形。

播放段落

6. Find the line parallel to $\begin{align*}y=3x-5 \end{align*}$ that passes through $\begin{align*}(2,11).\end{align*}$
::6. 找到与y=3x-5平行的通过(2,11)的线条。

播放段落

7. Find the line perpendicular to $\begin{align*}y=3x-5\end{align*}$ that passes through $\begin{align*}(6,11).\end{align*}$
::7. 找到通过(6,11)的与y=3x-5垂直的直线(6,11)。

播放段落

8. Find the line parallel to $\begin{align*}3x+4y=7\end{align*}$ that passes through $\begin{align*}(4,2).\end{align*}$
::8. 找到与通过3x+4y=7(4,2)的3x+4y=7平行的线条。

播放段落

9. Find the line perpendicular to $\begin{align*}3x+4y=7\end{align*}$ that passes through $\begin{align*}(3,10).\end{align*}$
::9. 找到穿透3x+4y=7的垂直直线(3,10)。

播放段落

10. Find the line parallel to $\begin{align*}y=5\end{align*}$ that passes through $\begin{align*}(2,16).\end{align*}$
::10. 找到与y=5平行的通过(2,16)的线。

播放段落

11. Find the line perpendicular to $\begin{align*}y=5\end{align*}$ that passes through $\begin{align*}(2,16)\end{align*}$
::11. 找到通过(2,16)的与y=5垂直的直线。

播放段落

12. Find the line parallel to $\begin{align*}y=-\frac{1}{3}x-4\end{align*}$ that passes through $\begin{align*}(6,8).\end{align*}$
::12. 找到与通过Y13x-4(6,8)线平行的线条。

播放段落

13. Find the line perpendicular to $\begin{align*}y=-\frac{1}{3}x-4\end{align*}$ that passes through $\begin{align*}(6,8).\end{align*}$
::13. 找到贯穿于y13x-4的直线(6,8)。

播放段落

14. Line $\begin{align*}a\end{align*}$ passes through the point $\begin{align*}(2,4)\end{align*}$ and $\begin{align*}(3,6)\end{align*}$ . Line $\begin{align*}b\end{align*}$ passes through the points $\begin{align*}(6,7)\end{align*}$ and $\begin{align*}(11,17)\end{align*}$ . Are lines $\begin{align*}a\end{align*}$ and $\begin{align*}b\end{align*}$ parallel, perpendicular, or neither?
::14. 一行通过点(2、4和3、6),一行通过点(6、7和11、17),一行通过点(6、7和11、17)。

播放段落

15. Line $\begin{align*}a\end{align*}$ passes through the point $\begin{align*}(1,-1)\end{align*}$ and $\begin{align*}(6,14)\end{align*}$ . Line $\begin{align*}b\end{align*}$ passes through the points $\begin{align*}(9,3)\end{align*}$ and $\begin{align*}(-6,8)\end{align*}$ . Are lines $\begin{align*}a\end{align*}$ and $\begin{align*}b\end{align*}$ parallel, perpendicular, or neither?
::15. 线一行通过点(1,-1)和(6,14),线b通过点(9,3)和(-6,8),线一行和线一行和线二行平行、垂直,还是两者都不平行?

播放段落

16. A new amusement park is going to be built near two major highways. On a coordinate grid of the area, with scale 1 unit representing 1 km, the park is located at point $\begin{align*}P(3, 4).\end{align*}$ Highway 2 is represented by the equation $\begin{align*}y = 2x + 5,\end{align*}$ and Highway 10 is represented by the equation $\begin{align*}y = -­0.5x + 2.\end{align*}$ Determine the coordinates of the exits that must be built on each highway to result in the shortest road to the park.
::16. 将在两条主要公路附近建造一个新的游乐公园,在坐标网上,面积为1级,面积为1公里,公园位于P(3.4)点,2号公路的方程为y=2x+5,10号公路的方程为y0.5x+2,确定每个公路必须修建的出入口的坐标,以修建通往公园的最短道路。

播放段落

17. Determine if the points A(1, -2), B(4, 4), and C(5, 6) are collinear.
::17. 确定A(1)、B(4)、B(4)和C(5)、C(5)、C(6)点是否合线。

播放段落

18. Find the value of b given that A(-6, 2), B(b, 0), and C(3, -4) are collinear.
::18. 鉴于A(-6, 2),B(b, 0)和C(3, 4)为合线,确定b(6, 2)的值。

播放段落

19. Determine the value of k for which the lines $\begin{align*}kx-2y-1=0\end{align*}$ and $\begin{align*}8x-ky+3=0\end{align*}$ are parallel. How does the value change if the lines are perpendicular? Can there be more than one value for k?
::19. 确定行为 kx- 2y- 1=0 和 8x- ky+3=0 平行的 k 值。 如果行是垂直的, 该值如何变化? k 是否有一个以上的值 ?

播放段落

20. Construct the equations of lines that form a square or a rectangle such that no sides are vertical or horizontal.
::20. 构建构成正方形或矩形的线条方程式,以便没有垂直或水平的侧面。

播放段落

Review (Answers)
::审查(答复)

播放段落

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。