Section: 赤道不平等 | 3.5 赤道不平等-interactive

Section outline

Lesson Objectives
::经验教训目标

Solve real-world problems involving a quadratic inequality graphically.
::解决现实世界的问题涉及二次不平等的图形化。

Solve real-world problems by solving a quadratic inequality algebraically.
::解决现实世界的问题解决二次不平等的代数。

Graph a quadratic inequality.
::绘制二次不平等的图。

Introduction: Fear of Heights
::导言:对高地的恐惧

Q uadratic equations have either 0, 1, or 2 valid solutions in the context of the problem. H owever, problems often have a range of acceptable solutions that can be expressed using inequalities.
::在问题的背景下,赤道方程式有0、1或2个有效的解决办法,但问题往往有一系列可以接受的解决办法,可以用不平等来表达。

Example
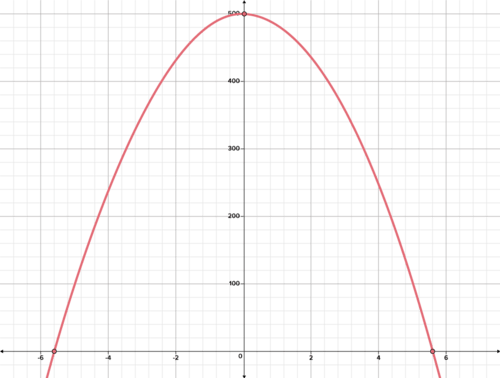
::示例示例示例示例

Chase is a stunt man who is base jumping from a bridge 500 feet above a river for a movie. He needs to pull the cord on his parachute between 400 and 275 feet. His height during the fall is defined by the function $\begin{aligned} h (t) = 500 - 16 t^{2} . \end{aligned}$ Write an inequality for the times during which he should pull his parachute.
::大通是一个特技演员,他正在从河上500英尺高的桥上跳跃,看电影。他需要拉起降落伞的绳索,在400至275英尺之间。他跌倒时的高度由函数 h(t)=500-16t2确定。写下他拉降落伞时的不平等。

Discuss how you might begin to approach this problem. The next activity will explore this problem further.
::讨论您可能如何开始处理这一问题。下一步活动将进一步探讨这个问题。

Activity 1: Solving Quadratic Inequalities Graphically
::活动1:用图形方式解决赤道不平等问题

Graphing a function is a good way to help to visualize every possible solution. A graph can be used to identify the solutions that will satisfy certain conditions.
::绘制函数图是帮助想象每一种可能的解决方案的好方法。图表可用于确定符合某些条件的解决方案。

To solve the problem in the introduction, look at a graph of the function $\begin{aligned} h (t) = 500 - 16 t^{2} . \end{aligned}$
::要解决导言中的问题,请查看函数 h(t) = 500- 16t2 的图示。

The condition that Chase needs to pull the cord on his parachute between 400 and 275 feet can be expressed using inequalities:
::大通需要将降落伞的绳索拉到400至275英尺之间,

$\begin{aligned} 275 \leq 500 - 16 t^{2} \leq 400 \end{aligned}$

::275 - 500 - 16t-2400

T he inequality can be broken apart into three pieces to get a better idea of what the conditions look like on a graph:
::不平等可以分成三部分, 以便更清楚地了解图表上的状况:

$\begin{aligned} h (t) = 500 - 16 t^{2} \end{aligned}$
::h(t)=500-16t2

$\begin{aligned} h (t) \geq 275 \end{aligned}$
:t)_____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

$\begin{aligned} h (t) \leq 400 \end{aligned}$
:t)4000

Use the graph above to answer the following questions.
::使用上图回答下列问题。

Activity 2: Solving Quadratic Inequalities Algebraically
::活动2:用代数法解决赤道不平等问题

While graphs are a useful method for solving inequalities, an algebraic approach can also be taken. The lesson Roots of Quadratic Functions introduced this example :
::虽然图表是解决不平等问题的有用方法,但也可以采用代数法。

A firework is launched from a platform 29 feet off the ground with an initial velocity of 112 ft/s. The height of the firework can be modeled as a function of time using the function $\begin{aligned} h (x) = - 16 x^{2} + 112 x + 29. \end{aligned}$ The firework must go off at 200 feet, to ensure the safety of the onlookers.
::从离地29英尺的平台上发射烟花,最初速度为112英尺/秒。烟花的高度可以用h(x)16x2+112x+29的功能作为时间函数模型。烟花必须以200英尺的速度起落,以确保旁观者的安全。

Suppose the firework had to go off at least 200 feet from the ground. A t what times could the firework go off?
::如果烟花离地至少200英尺烟花什么时候会熄灭呢?

Example
::示例示例示例示例

Solve the inequality $\begin{aligned} 200 \leq - 16 x^{2} + 112 x + 29. \end{aligned}$
::解决不平等问题 20016x2+112x29。

The process for solving quadratic inequalities is similar to quadratic equations. First, subtract 200 from both sides of the inequality.
::解决二次不平等的过程与二次等式相似。首先,从两边减去200个不平等。

$\begin{aligned} 200 & \leq - 16 x^{2} + 112 x + 29 \\ - 200 & - 200 \\ 0 & \leq - 16 x^{2} + 112 x - 171 \end{aligned}$

::20016x2+112x+29-200-2000}16x2+112x-171

Next, factor the expression $\begin{aligned} - 16 x^{2} + 112 x - 171. \end{aligned}$
::下一个乘数表示式 - 16x2+112x-171。

$\begin{aligned} 0 \leq - 16 x^{2} + 112 x - 1710 \leq - (4 x - 9) (4 x - 19) \end{aligned}$

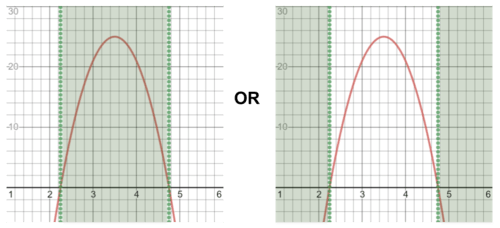
::016x2+112x-1710(4x-9)(4x-19)

T he expression $\begin{aligned} - (4 x - 9) (4 x - 19) \end{aligned}$ must be greater than or equal to zero. T he values that make the expression $\begin{aligned} - (4 x - 9) (4 x - 19) \end{aligned}$ equal to zero are $\begin{aligned} \frac{9}{4} = 2.25 and \frac{19}{4} = 4.75. \end{aligned}$ Since this function forms a parabola when graphed, all positive values must either be inside or outside the $\begin{aligned} x \end{aligned}$ - intercepts .
::表达式 -( 4x- 9) ( 4x-19) 必须大于或等于零。使表达式 -( 4x- 9) ( 4x-19) 等于零的值为 94= 2. 25 和 194= 4. 75。由于此函数在图形化时构成抛物线, 所有正值都必须在 x 界面内或外方。

T est a value between 2.25 and 4.75 to see if it will make $\begin{aligned} - (4 x - 9) (4 x - 19) \end{aligned}$ positive. If the answer is positive, all values between 2.25 and 4.75 will make the inequality true. Otherwise, all values outside of 2.25 and 4.75 will make the inequality true.
::测试值在 2. 25 和 4. 75 之间, 以确定它是否会使 -( 4x- 9) ( 4x-19) 呈正数。如果答案是正数, 则2. 25 和 4. 75 之间的所有数值都会使不平等成为事实。否则, 2. 25 和 4. 75 之外的所有数值都会使不平等成为事实。

Testing $\begin{aligned} x = 3, \end{aligned}$
::测试x=3,测试x=3

$\begin{aligned} (- 4 (3) + 9) (4 (3) - 19) & = (- 12 + 9) (12 - 19) \\ = (- 3) (- 7) \\ = 21 \end{aligned}$

Since 3 makes the expression positive, all values between 2.25 and 4.75 will make the expression $\begin{aligned} (- 4 x + 9) (4 x - 19) \end{aligned}$ positive. This means that all values between 2.25 and 4.75 will be above 200 feet in the function $\begin{aligned} h (x) = - 16 x^{2} + 112 x + 29. \end{aligned}$
::由于3 表示为正, 2. 25 至 4. 75 之间的所有值将使表达式( - 4x+9) (4x-19) 变为正,这意味着2. 25 至 4. 75 之间所有值在函数 h(x)\\ 16x2+112x+29 中将超过200英尺。

Answer: $\begin{aligned} 2.25 \leq x \leq 4.75 \end{aligned}$
::答复:2.25x4.75

The firework can go off any time between 2.25 seconds and 4.75 seconds
::烟花可以随时在2.25秒到4.75秒之间熄灭

Discussion Question : Could you have determined that any $\begin{aligned} x \end{aligned}$ -value between the $\begin{aligned} x \end{aligned}$ -intercepts would result in a positive output based on the $\begin{aligned} a \end{aligned}$ - coefficient ?
::讨论问题:你是否能够确定,在X接口之间有任何x值会导致基于系数效率的正产出?

Activity 3: Quadratic Inequalities With Two Variables
::活动3:具有两个变量的赤道不平等

T he graph of a linear inequality will display all possible coordinates that satisfy the conditions of the inequality.
::线性不平等图将显示满足不平等条件的所有可能的坐标。

To get a sense of how the graphs of quadratic inequalities with two variables will look, test a few points in the interactive below to see if they satisfy the conditions of the inequality.
::为了了解带有两个变量的二次不平等的图表将如何看, 测试下面互动的几点, 看看它们是否符合不平等的条件。

INTERACTIVE

Quadratic Inequalities With Two Variables

Use the interactive to graph five test points on the inequality @$y \geq x^2 - 5x + 7@$ .
::使用互动来图示不平等的五个测试点@$y\geq x%2 - 5x+7@$。

For each point, fill in the first blank with the y-coordinate of the point. Fill in the second blank by plugging the x-coordinate into the equality.
::对于每个点, 请用点的 Y 坐标填入第一个空格。将 x 坐标插入等距。

Compare the two values and decide if each point satisfies the equality.
::比较两种价值观,决定每一点是否符合平等。

Generate more random coordinates to finish the graph.
::生成更多随机坐标以完成图形。

Your device seems to be offline.
Please check your internet connection and try again.

+

Do you want to reset the PLIX?

Yes

No

To graph an inequality with two variables, first graph the function. As shown in the interactive above, all solutions will either be inside or outside of the parabola.
::要用两个变量绘制不平等图,请先绘制函数图。如上互动图所示,所有解决方案要么在抛物线内,要么在抛物线外。

To determine whether to shade inside or outside the parabola, choose one point that is either inside or outside of the parabola and check it.
::为了确定抛物线内外的阴影,选择一个在抛物线内外的点并检查它。

If the coordinate makes the inequality true, then shade the same side of the parabola that the coordinate is on.
::如果坐标使不平等成为真实,则将坐标所在的抛物线的同一面遮蔽。

If the coordinate makes the inequality false, then shade the opposite side of the parabola that the coordinate it on.
::如果坐标显示不平等是假的, 则将协调的抛物线的反面遮蔽。

Recall from linear inequalities that the < or > symbols indicate using a dotted line to graph the linear function because it excludes points that would make both sides of the function equal. The same holds for quadratic inequalities: the < or > symbols will result in a dotted parabola and the ≤ or ≥ symbols will result in a solid parabola.
::从线性不平等中回顾, < 或 > 符号表示用虚线来显示线性函数,因为它排除了使函数两侧相等的点。对二次不平等来说, " 或 > 符号将产生虚线抛物线,而或或符号将产生坚固的抛物线。

Discussion Question : A firework that is launched can be modeled using the function $\begin{aligned} h (x) = - 16 x^{2} + 112 x + 29. \end{aligned}$ Will every height produce a positive and negative answer? Which times and heights can you exclude from your solution set ? What would the graph look like with these taken into account?
::讨论问题: 使用函数 h( x)\\\ 16x2+112x+29可以模拟启动的烟火。每个高度是否都产生正反回答? 您能将哪些时间和高度排除在解决方案集之外吗? 图表将如何看待这些考虑?

Wrap-Up: Review Questions
::总结:审查问题

Summary
::摘要

When solving a quadratic inequality rewrite the equation so it is in the form:
::当解决二次不平等时重写方程式时, 它以形式出现 :

$\begin{aligned} 0 \leq a x^{2} + b x + c \end{aligned}$ and find the values that make the inequality positive.
::0ax2+bx+c 并找到使不平等成为正数的价值观。

$\begin{aligned} 0 \geq a x^{2} + b x + c \end{aligned}$ and find the values that make the inequality negative.
::0ax2+bx+c 并找到不平等负值。

When graphing a quadratic inequality of one variable, the solutions can be found either between the roots or outside of the roots.
::当绘制一个变量的二次不平等图时,可以在根或根之外找到解决办法。

When graphing a quadratic inequality of two variables, the solutions can be found either inside or outside the parabola.
::当绘制两个变量的二次不平等图时,可以在抛物线内外找到解决办法。

Section outline

Introduction: Fear of Heights ::导言:对高地的恐惧

Activity 1: Solving Quadratic Inequalities Graphically ::活动1:用图形方式解决赤道不平等问题

Activity 2: Solving Quadratic Inequalities Algebraically ::活动2:用代数法解决赤道不平等问题

Activity 3: Quadratic Inequalities With Two Variables ::活动3:具有两个变量的赤道不平等

Wrap-Up: Review Questions ::总结:审查问题

Summary ::摘要

Introduction: Fear of Heights
::导言:对高地的恐惧

Activity 1: Solving Quadratic Inequalities Graphically
::活动1:用图形方式解决赤道不平等问题

Activity 2: Solving Quadratic Inequalities Algebraically
::活动2:用代数法解决赤道不平等问题

Activity 3: Quadratic Inequalities With Two Variables
::活动3:具有两个变量的赤道不平等

Wrap-Up: Review Questions
::总结:审查问题

Summary
::摘要