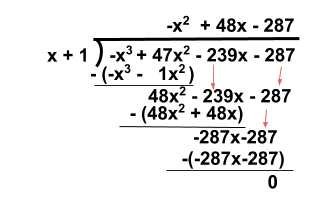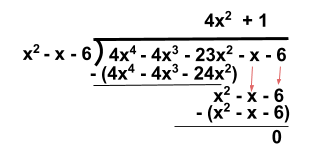节: 多元等同根 | 4.4 多元等同的根-interactive

章节大纲

Lesson Objectives
::经验教训目标

Interpret the characteristics of a polynomial within a real-world context.
::在现实世界背景下解释多元性的特点。

Use the Rational Zeros Theorem and division to find the zeroes and possible zeros of a polynomial with degree greater than two.
::使用理性的零点理论和分解来找到一个大于2度的多元数值的零和可能的零。

Understand the .
::理解这一点。

Identify the zeros of a polynomial given the graph.
::标记图形给出的多面体数的零。

Write and solve a polynomial within a real-world or mathematical context.
::在现实世界或数学背景下写并解析一个多义。

Introduction: Container Volume Problem - Thick Walls
::导言:集装箱数量问题 -- -- 厚墙壁

Use the interactive below to explore how to find the volume of different size containers that have walls that are 1 inch thick.
::使用下面的交互方式来探索如何找到墙壁厚1英寸的不同尺寸集装箱的容量。

INTERACTIVE

Container Problem Revisited

This cube container has walls which are 1 inch thick.
::这个立方体容器有1英寸厚的墙壁

Use the slider to change the side length of the cube.
::使用滑块更改立方体的侧长度。

In this lesson, you will investigate the following questions:
::在这一教训中,你将调查下列问题:

What expressions could be used to model the side lengths?
::可使用什么表达式来模拟侧边长度?

What polynomial could be used to model the volume the container can support?
::容器能够支撑的体积可使用何种多式模型?

What size would the side length of the cube need to be to hold 150 cubic inches?
::立方体的侧长需要多少大小才能保持150立方英寸?

Activity 1: Factored Form
::活动1:有因数形式

To solve the problem above, you will need to know more about the zeros of a polynomial function . The zeros of a polynomial function are the $\begin{aligned} x \end{aligned}$ - intercepts . Zeroes are also called roots in the context of a polynomial equation , where the term solutions may also apply .
::要解决上述问题, 您需要了解更多关于多元函数的零。多元函数的零是 X 截取。在多元方程式的背景下, 零也被称为根。在多元方程式中, 也可以使用术语解决方案。

To help visualize zeros, revisit the example from the section Using Quadratic Methods.
::为帮助直观化零,请在“使用二次曲线方法”一节中重温这个例子。

Example
::示例示例示例示例

The concentration, in parts per million, of a medicine in a patient’s bloodstream after $\begin{aligned} x \end{aligned}$ hours can be modeled using the function $\begin{aligned} C (x) = 0.002 x^{3} - 0.16 x^{2} + 3.2 x, \end{aligned}$ given a specific domain . What are the zeros of this function ? What do they mean in context?
::病人在x小时后的血液中的药物浓度,每百万分之一的浓度,可以用功能C(x)=0.002x3-0.16x2+3.2x来模拟。根据特定域,该函数的零值是多少?在上下文中它们意味着什么?

The polynomial can be factored as follows:
::多元性可考虑如下:

\begin{aligned} 0.002 x^{3} - 0.16 x^{2} + 3.2 x = 0.002 x (x - 40) (x - 40) \end{aligned}

::0002x3-0.16x2+3.2x=0.002x(x-40)(x-40)

The graph of this polynomial is:
::此多面体的图示是 :

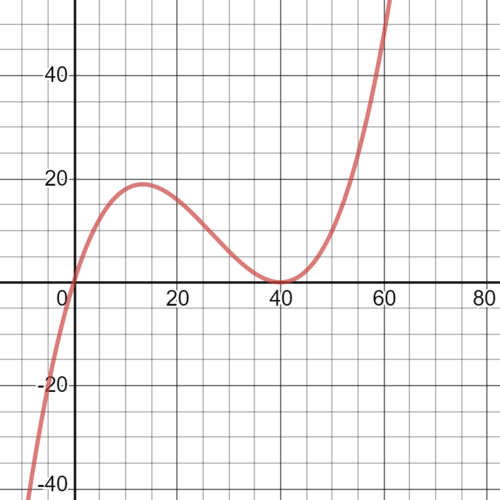
lesson content

Use the graph and the factored form of the polynomial to answer the questions below.
::使用图形和多数值的因子形式回答下面的问题。

Discussion Question : Write a non-linear polynomial function in factored form that has one zero . W rite a non- quadratic function in factored form that has two zeros.
::讨论问题: 以系数为零以非线性多元函数写成。以系数为零以二为零以非线性多元函数写成。以系数为零以二为零以非二次的二次函数写成。

When the solutions or $\begin{aligned} x \end{aligned}$ -intercepts repeat, this refers to the multiplicity of that solution. A solution that occurs once has a multiplicity of 1, a solution that occurs twice has a multiplicity of 2, a solution that occurs three times has a multiplicity of 3, etc.
::当解决方案或 X 界面重复时, 这里指的是该解决方案的多重性。一旦出现的解决办法有多重性 1, 两次出现的解决办法有多重性 2, 三次出现的解决办法有多重性 3 等。

In the example $\begin{aligned} C (x) = 0.002 x (x - 40) (x - 40), \end{aligned}$ the solutions are 0 and 40. The solution 40 has a multiplicity of 2 because it occurs twice. In the next activity, you will explore the effect that m ultiplicity has on the graph of a polynomial function.
::在C(x)=0.002x(x-40)(x-40)(40)的示例中,解决办法是0和40。40的答案是40。40的答案是2倍,因为它发生两次。在下一个活动中,你将探讨多重性对多元函数图形的影响。

Activity 2: Rational Zeroes Theorem
::活动2:理性零点理论

Factoring a polynomial function can help you to easily identify the zeros because it allows you to use the zero product property .
::乘以一个多元函数可以帮助您很容易地识别零,因为它允许您使用零产品属性。

Example
::示例示例示例示例

A furniture company performed an analysis on one of the couches they sell.
::一家家具公司对其出售的沙发之一进行了分析。

The revenue as a function of selling $\begin{aligned} x \end{aligned}$ couches can be modeled by the function $\begin{aligned} R (x) = 47 x^{2} - x^{3} . \end{aligned}$
::销售 x 沙发的收入函数,可以用 R(x) = 47x2 - x3 函数模拟。

The monthly cost of selling $\begin{aligned} x \end{aligned}$ couches can be modeled using $\begin{aligned} C (x) = 239 x + 287. \end{aligned}$
::可使用C(x)=239x+287模拟出售x沙发的月成本。

The profit function can be modeled using the polynomial $\begin{aligned} P (x) = - x^{3} + 47 x^{2} - 239 x - 287. \end{aligned}$
::利润函数可使用多边 P(x) x3+47x2-239x-287模型构建。

Use algebraic methods to find the zeroes of this function.
::使用代数方法查找此函数的零。

INTERACTIVE

Comparing Graphs

Use the dropdown menu to switch between graphs.
::使用下拉菜单在图形之间切换。

Click the red points to see their values.
::单击红点以查看它们的值。

T here are not any quadratic methods that will work for this case. Instead, t he function $\begin{aligned} P (x) = - x^{3} + 47 x^{2} - 239 x - 287 \end{aligned}$ can be written in factored form using the R ational F actors T heorem. The factors of the leading coefficient , -1, are ± 1. The factors of the constant , -287, are ±1, ±7, ±41, ±287. The possible rational factors are:
::不存在适用于此案例的任何二次曲线方法。相反, 函数 P( x) x3+47x2-2-239x-287可以使用理性因素理论以系数形式写成。主要系数-1的系数为 +1。常数- 287的系数为 +1, +7, 41, 287, 可能的理性因素为 :

$\begin{aligned} (1 x + 1), \end{aligned}$ $\begin{aligned} (1 x - 1), \end{aligned}$ $\begin{aligned} (1 x + 7), \end{aligned}$ $\begin{aligned} (1 x - 7), \end{aligned}$ $\begin{aligned} (1 x + 41), \end{aligned}$ $\begin{aligned} (1 x - 41), \end{aligned}$ $\begin{aligned} (1 x + 287), \end{aligned}$ $\begin{aligned} (1 x - 287), \end{aligned}$ $\begin{aligned} (- 1 x + 1), \end{aligned}$ $\begin{aligned} (- 1 x - 1), \end{aligned}$ $\begin{aligned} (- 1 x + 7), \end{aligned}$ $\begin{aligned} (- 1 x - 7), \end{aligned}$ $\begin{aligned} (- 1 x + 41), \end{aligned}$ $\begin{aligned} (- 1 x - 41), \end{aligned}$ $\begin{aligned} (- 1 x + 287), \end{aligned}$ $\begin{aligned} (- 1 x - 287) \end{aligned}$
:1x+1)、(1x-1)、(1x-1)、(1x+7)、(1x-7)、(1x-7)、(1x+41)、(1x-41)、(1x+287)、(1x-287)、(1x-287)、(1x-1x+1)、(-1x-1/1)、(-1x+7)、(-1x-7)、(-1x+41)、(-1x-41)、(1x+287)、(-1x-287)

B egin by testing $\begin{aligned} (1 x + 1) \end{aligned}$ and continue through the list until you find a factor . Keep in mind that none of these may be factors.
::开始测试( 1x+1) , 并在列表中继续直到您找到一个系数。请记住, 这些要素都不是因素。

lesson content

Since the remainder is 0, $\begin{aligned} x + 1 \end{aligned}$ is a factor of $\begin{aligned} - x^{3} + 47 x^{2} - 239 x - 287. \end{aligned}$ Furthermore , the quotient when $\begin{aligned} - x^{3} + 47 x^{2} - 239 x - 287 \end{aligned}$ is divided by $\begin{aligned} x + 1 \end{aligned}$ is $\begin{aligned} - x^{2} + 48 x - 287. \end{aligned}$ Thus, the polynomial can be written as:
::由于其余为0,x+1是-x3+47x2-239x-239x-287的乘数,因此,当-x3+47x2-2-239x-287除以x+1时,多数值可以写成:

\begin{aligned} - x^{3} + 47 x^{2} - 239 x - 287 = (x + 1) (- x^{2} + 48 x - 287) \end{aligned}

::-x3+47x2-239x-287=(x+1)(-x2+48x-287)

The quadratic factor $\begin{aligned} - x^{2} + 48 x - 287 \end{aligned}$ can be further factored into $\begin{aligned} (- 1 x + 7) (x - 41) . \end{aligned}$ It is customary to factor out negative leading coefficients as well. For example, $\begin{aligned} (- 1 x + 7) \end{aligned}$ can be rewritten as $\begin{aligned} (x - 7), \end{aligned}$ so the polynomial in factored form is:
::二次系数-x2+48x-287可以进一步纳入(-1x+7)(x-41),通常也考虑负主要系数。例如,(-1x+7)可以改写为(x-7),因此,系数形式的多数值为:

\begin{aligned} - x^{3} + 47 x^{2} - 239 x - 287 = - (x + 1) (x - 7) (x - 41) \end{aligned}

::-x3+47x2-2-239x-287(x+1)(x-7)(x-41)

U sing the zero product property, find the zeros of the function as follows:
::使用零产品属性,查找函数的零如下:

• $\begin{aligned} - 1 \neq 0 \end{aligned}$

• $\begin{aligned} x + 1 = 0 \to x = - 1 \end{aligned}$
::• x+1=0x%1

• $\begin{aligned} x - 7 = 0 \to x = 7 \end{aligned}$
::• x-7=0x=7

• $\begin{aligned} x - 41 = 0 \to x = 41 \end{aligned}$
::• x-41=0x=41

Answer: The zeros of $\begin{aligned} P (x) \end{aligned}$ are -1, 7, and 41.
::答复:P(x)零是-1、7和41。

The zeros of the profit function represent the break-even points. If the price is set to $7 or $41, the company will make $0 profit. The zero at -1 should be ignored because the price cannot be set to -$1. In general, the domain of the profit function only includes prices greater than or equal to 0, or $\begin{aligned} x \geq 0. \end{aligned}$
::利润函数的零代表平衡点。如果价格定在7美元或41美元, 公司将产生0美元利润。以 - 1 的零应该忽略, 因为价格不能定在 - 1 美元。一般来说, 利润函数的域只包括大于或等于 0 或 x+0 的价格。

Since the factors of a polynomial determine the zeros ( t he factor $\begin{aligned} a x - b \end{aligned}$ will have a zero at $\begin{aligned} \frac{b}{a}), \end{aligned}$ the R ational F actors T heorem can be extended to zeros.
::由于多元系数的系数决定零(系数ax-b在巴巴为零),理性系数理论可以扩大到零。

Rational Zeros Theorem
::理性零点定理

\begin{aligned} \frac{q}{p} \end{aligned}

is a zero of the polynomial function

\begin{aligned} p (x) \end{aligned}

with integer coefficients, then

\begin{aligned} q \end{aligned}

is a factor of the constant term, and

\begin{aligned} p \end{aligned}

is a factor of the leading coefficient.

Activity 3: The Fundamental Theorem of Algebra
::活动3:代数的基本理论

The chapter Functions explored the Fundamental Theorem of Algebra in quadratics. A ll degree 2 functions have 2 roots.
::本章“函数”探讨了二次方位代数的基本理论。所有二级函数都有2个根。

From this, you might speculate that a function of degree $\begin{aligned} n \end{aligned}$ would have $\begin{aligned} n \end{aligned}$ roots. This conjecture is the Fundamental Theorem of Algebra .
::由此,你可能会推测, 程度 n 的函数有正根。这个猜想是代数的基本理论。

The Fundamental Theorem of Algebra
::代数基本理论

Any polynomial with complex coefficients of degree

\begin{aligned} n \end{aligned}

has

\begin{aligned} n \end{aligned}

complex roots, including repeated roots.

Although some roots may not be rational, they still exist as irrational or complex roots.
::虽然有些根源可能不合理,但它们作为不合理或复杂的根源仍然存在。

Example
::示例示例示例示例

Find the zeros of the function: $\begin{aligned} f (x) = 4 x^{4} - 4 x^{3} - 23 x^{2} - x - 6 \end{aligned}$
::查找函数的零: f(x)=4x4-4x4-4x3-23x2-x-6

To find the zeros of a function, a n alternative to using the R ational Z eros T heorem is using a graph. Use the graph below to find any rational zeros of $\begin{aligned} f (x) . \end{aligned}$
::要找到函数的零, 使用理性零点理论的替代方法正在使用一个图形。使用下方的图形来查找任何f( x) 的理性零。

The graph shows two zeros: -2 and 3. However, according to the Fundamental Theorem of Algebra, there should be 4 roots because this is a degree 4 polynomial.
::该图显示两个零:-2和3。然而,根据代数的基本理论,应该有4根根,因为这是4度多义。

T he missing roots are not irrational because irrational roots cross the $\begin{aligned} x \end{aligned}$ -axis at irrational values. Since there are no other $\begin{aligned} x \end{aligned}$ -intercepts , the missing roots must be complex.
::缺失的根不是非理性的,因为非理性的根以非理性的值跨越 X 轴。因为没有其他的 X 拦截, 缺失的根必须复杂。

To find the complex roots, start by dividing the polynomial by the known factors. The root -2 means that $\begin{aligned} x + 2 \end{aligned}$ is a factor of $\begin{aligned} f (x) \end{aligned}$ and the root 3 means that $\begin{aligned} x - 3 \end{aligned}$ is also a factor of $\begin{aligned} f (x) . \end{aligned}$
::要找到复杂的根根, 首先从已知因素除以多元系数开始。根 - 2 意味着 x+2 是 f( x) 的因数, 根 3 意味着 x-3 也是 f( x) 的因数。

You could either divide by these factors one by one using synthetic division , or multiply them together and divide by the resulting product . This would be similar to how dividing 12 by 2 and then by 3 is the same as dividing 12 by 6.
::您可以用合成分裂法将这些因素一一地除以,也可以用合成分裂法将这些因素一一地相除,或者将这些因素相乘,然后用所产生的产品加以除以。这类似于12除以2,然后再除以3等于12除以6。

The factors multiply to $\begin{aligned} (x + 2) (x - 3) = x^{2} - x - 6. \end{aligned}$ U se long division to divide $\begin{aligned} 4 x^{4} - 4 x^{3} - 23 x^{2} - x - 6 \end{aligned}$ by $\begin{aligned} x^{2} - x - 6. \end{aligned}$
::乘以 (x+2)(x-3) =x2-x-6) 乘以 (x2-x3) =x2-x-6 。

lesson content

The division problem above can be written as:
::上面的划分问题可以写为:

\begin{aligned} 4 x^{4} - 4 x^{3} - 23 x^{2} - x - 6 = (x^{2} - x - 6) (4 x^{2} + 1) \end{aligned}

::4x4-4x3-23x2-x-6=(x2-x-6)(4x2+1)

This can be factored since $\begin{aligned} x^{2} - x - 6 = (x + 2) (x - 3) . \end{aligned}$
::从 x2 - x - 6= (x+2)(x- 3) 开始可以计算。

\begin{aligned} 4 x^{4} - 4 x^{3} - 23 x^{2} - x - 6 = (x + 2) (x - 3) (4 x^{2} + 1) \end{aligned}

::4x4-4x3-23x2-x-6=(x+2)(x-3)(4x2+1)

Although the quadratic $\begin{aligned} 4 x^{2} + 1 \end{aligned}$ cannot be factored using rational numbers, t he zeros can be found using the square root method.
::虽然方形 4x2+1 无法使用合理数字进行系数计算,但可用平方根法找到零。

\begin{aligned} x + 2 & = 0 \\ - 2 & - 2 \\ x & = - 2 \end{aligned}

\begin{aligned} x - 3 & = 0 \\ + 3 & + 3 \\ x & = 3 \end{aligned}

\begin{aligned} 4 x^{2} + 1 & = 0 \\ - 1 & - 1 \\ 4 x^{2} & = - 1 \\ \div 4 & \div 4 \\ x^{2} & = - \frac{1}{4} \\ \sqrt{x^{2}} & = \sqrt{- \frac{1}{4}} \\ x & = \pm i \sqrt{\frac{1}{4}} \\ x & = \pm \frac{1}{2} i \end{aligned}

Answer: $\begin{aligned} - 2, 3, \frac{1}{2} i, - \frac{1}{2} i \end{aligned}$
::答复:-2,3,12i,-12i

Discussion Question : Is it possible for a polynomial to have an odd number of complex roots?
::讨论问题:多族制是否可能有数量奇多的复杂根根?

Activity 4: The Container Problem Solved
::活动4:解决集装箱问题

Answer the questions below to solve the problem asked in the introduction: What size would the sides of the cube need to be to hold 150 cubic inches?
::回答以下问题以解决导言中提出的问题:立方体的两侧需要多少尺寸才能保持150立方英寸?

Recall the container problem and interactive from the introduction:
::回顾前言中的集装箱问题和互动:

INTERACTIVE

Container Problem Revisited

This cube container has walls which are 1 inch thick.
::这个立方体容器有1英寸厚的墙壁

Use the slider to change the side length of the cube.
::使用滑块更改立方体的侧长度。

Discussion Question : How could you solve the container problem without rewriting the equation into standard form ?
::讨论问题:如果不将等式改写成标准形式,你如何解决集装箱问题?

Wrap-Up: Review Questions
::总结:审查问题

Summary
::摘要

The zeros of a polynomial function are the $\begin{aligned} x - \end{aligned}$ intercepts.
::多面函数的零是 X 界面。

The Rational Zeros Theorem states that if $\begin{aligned} \frac{q}{p} \end{aligned}$ is a zero of the polynomial function $\begin{aligned} p (x) \end{aligned}$ with integer coefficients, then $\begin{aligned} q \end{aligned}$ is a factor of the constant term, and $\begin{aligned} p \end{aligned}$ is a factor of the leading coefficient.
::理性零理论指出,如果qp是具有整数系数的多元函数p(x)的零,则q是常数的一个系数,p是主要系数的一个系数。

The Fundamental Theorem of Algebra states that any polynomial with complex coefficients of degree $\begin{aligned} n \end{aligned}$ has $\begin{aligned} n \end{aligned}$ complex roots, including repeated roots.
::代数的基本理论指出,任何具有复杂程度系数的多元性,都有复杂的根部,包括反复的根部。

章节大纲

Introduction: Container Volume Problem - Thick Walls ::导言:集装箱数量问题 -- -- 厚墙壁

Activity 1: Factored Form ::活动1:有因数形式

Activity 2: Rational Zeroes Theorem ::活动2:理性零点理论

Rational Zeros Theorem ::理性零点定理

Activity 3: The Fundamental Theorem of Algebra ::活动3:代数的基本理论

The Fundamental Theorem of Algebra ::代数基本理论

Activity 4: The Container Problem Solved ::活动4:解决集装箱问题

Wrap-Up: Review Questions ::总结:审查问题

Summary ::摘要

Introduction: Container Volume Problem - Thick Walls
::导言:集装箱数量问题 -- -- 厚墙壁

Activity 1: Factored Form
::活动1:有因数形式

Activity 2: Rational Zeroes Theorem
::活动2:理性零点理论

Rational Zeros Theorem
::理性零点定理

Activity 3: The Fundamental Theorem of Algebra
::活动3:代数的基本理论

The Fundamental Theorem of Algebra
::代数基本理论

Activity 4: The Container Problem Solved
::活动4:解决集装箱问题

Wrap-Up: Review Questions
::总结:审查问题

Summary
::摘要