函数导言

播放段落

Functions in Computer Science
::计算机科学职能

播放段落

Computer Programming is a massive field that encompasses a range of jobs like app developers, database administrators, software developers, and many more. Functions play a major role in computer programming, so it just makes sense to  explore how they are used in this field. Functions are a major part of programming languages like Java, Python, and Swift, to name a few. A function in computer programming takes in a value, performs an operation  on it, and returns an output value. In computer programming, there are many different types of data that  you can enter into a function: integers , characters, boolean (true/false, yes/no, on/off), etc.  You will explore some of these over the course of the chapter. However, in mathematics,  you typically only use real numbers.
::计算机编程是一个庞大的域, 包括各种各样的工作, 比如 App 开发者、 数据库管理员、 软件开发者等 。 函数在计算机编程中扮演着主要角色, 所以探索这些功能如何用于此领域是有道理的。 函数是编程语言的主要部分, 比如 Java、 Python 和 Swift , 仅举几个例子。 计算机编程中的函数会以某种价值进行, 执行一个操作, 并返回一个输出值 。 在计算机编程中, 有许多不同类型的数据可以输入一个函数 : 整数、 字符、 布林( true/ false、 yes/ no、 op/ off) 等 。 您可以在章节中探索其中的一部分 。 然而, 在数学中, 您通常只使用真实数字 。

播放段落

A relation is a collection of ordered pairs which relate a set of input values to a set of output values. The input value is the value of the independent variable . The output value is the value of the dependent variable. Recall that the independent variable is the x-axis value, and the dependent variable is the y-axis variable. A special type of relation where every input has a single output it is called a function . The difference between functions and relations will be further explored in future sections. The basic idea behind relations and functions is that they are the rules which match input values with output values. This can be visualized in many different ways.
::关系是一个有顺序配对的集合, 将一组输入值与一组输出值联系起来。 输入值是独立的变量的值。 输出值是依附变量的值。 提醒注意, 独立变量是 X 轴值, 依附变量是 y 轴 变量。 每个输入有一个单一输出的一种特殊类型的关系, 它被称为函数。 函数和关系之间的差别将在未来的章节中进一步探讨。 关系和函数背后的基本理念是, 它们是将输入值与输出值匹配的规则。 这可以通过多种不同的方式进行可视化 。

 

---

播放段落

Visualizations of Relations and Functions
::关系和职能的视觉化

播放段落

Relations and functions can be written in many formats: a set of ordered pairs, a table, a mapping diagram, a graph, an equation . Let’s explore four different ways to represent a relation and break each one down.
::关系和函数可以多种形式写成:一连串有顺序的对子、一张表格、一张地图、一张图表、一张图表、一个方程式。 让我们探索四种不同的方式来代表一种关系并打破每一个关系。

播放段落

Set of Ordered Pairs
::一套有秩序对等

播放段落

When a relation is displayed as a set of ordered pairs, the  $\begin{align*}x\text{-}\end{align*}$ values represent the input values, and the $\begin{align*}y\text{-}\end{align*}$ values represent the output values.
::当关系显示为一组有顺序的配对时, x 值代表输入值, Y 值代表输出值。

播放段落

Example
::示例示例示例示例

$\begin{align*}\{(-4, 5), (0, 1), (2, 3), (6, -2), (7, 2)\}\end{align*}$

播放段落

Table
::表格表表表表

播放段落

When a relation is displayed in a table, each row represents an ordered pair with the  $\begin{align*}x\end{align*}$  column representing the input values and the  $\begin{align*}y\end{align*}$  column representing the output values.
::当在表格中显示一个关系时,每行代表一对有顺序的一对,带有 x 列,代表输入值和 Y 列,代表输出值。

播放段落

Example
::示例示例示例示例

$$\begin{align*}\large{\text{Input Values}}\end{align*}$$	$$\begin{align*}\large{\text{Output Values}}\end{align*}$$
$$\begin{align*}-4\end{align*}$$	$$\begin{align*}5\end{align*}$$
	$$\begin{align*}1\end{align*}$$
$$\begin{align*}2\end{align*}$$	$$\begin{align*}3\end{align*}$$
$$\begin{align*}6\end{align*}$$	$$\begin{align*}\text{-}2\end{align*}$$
$$\begin{align*}7\end{align*}$$	$$\begin{align*}2\end{align*}$$

播放段落

Mapping Diagram
::绘图图图图

播放段落

A mapping diagram uses arrows to visually map the set of input values onto the set of output values.
::映射图表使用箭头对输出值集的输入值集进行直观映射。

播放段落

Example  
::示例示例示例示例

播放段落

Graph
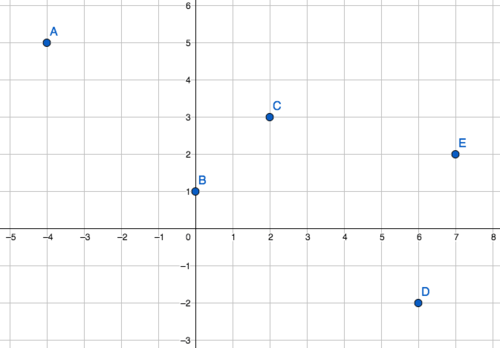
::图图图图图图图

播放段落

A graph displays the set of inputs and outputs as coordinates . The $\begin{align*}x\text{-}\end{align*}$ value represents the independent variable. The $\begin{align*}y\text{-}\end{align*}$ value represents the dependent variable.
::图表将输入和输出的一组显示为坐标。 x 值代表独立的变量。 Y 值代表独立的变量。

播放段落

Example
::示例示例示例示例

播放段落

Discussion Question
::讨论问题

播放段落

Grace claims that since each method displays the same function, it doesn't matter which you choose. Do you agree or disagree with Grace? When might one method for displaying a function be better than another?
::Grace 声称, 由于每种方法都显示相同的函数, 您选择哪个函数并不重要 。 您同意或不同意 Grace 吗 ? 显示函数的方法什么时候可以比其他方法更好 ?

---

播放段落

Make Your Own Function
::Make your own 函数

播放段落

All functions need a rule for determining the outputs for corresponding inputs. This rule can be complicated or as simple as adding one to the input.
::所有功能都需要有一条规则来确定相应输入的产出。 这一规则可能复杂, 或简单如在输入中添加一个。

播放段落

Use the interactive below to create your own function.
::使用下面的交互程序创建您自己的函数。

---

播放段落

Identify the Rule
::指明规则

播放段落

There will be real-world situations where you have to use a function to explain data. You  may have seen an example of this in the lesson ,  which demonstrated how  a line of best fit  might represent the data in a scatterplot. When the rule of a function determines the input and output values, you can use the values to determine the rule.
::将会有现实世界的情况, 您需要使用函数来解释数据。 您可能已经从课程中看到过这方面的一个例子, 该课展示了最合适的行如何代表分布图中的数据。 当函数的规则决定输入值和输出值时, 您可以使用数值来决定规则 。

播放段落

Example
::示例示例示例示例

播放段落

Find the rule for the function below.
::查找以下函数的规则。

$$\begin{align*}\large{\text{Input Values}}\end{align*}$$	$$\begin{align*}\large{\text{Output Values}}\end{align*}$$
$$\begin{align*}1\end{align*}$$	$$\begin{align*}9\end{align*}$$
$$\begin{align*}2\end{align*}$$	$$\begin{align*}11\end{align*}$$
$$\begin{align*}3\end{align*}$$	$$\begin{align*}13\end{align*}$$
$$\begin{align*}4\end{align*}$$	$$\begin{align*}15\end{align*}$$
$$\begin{align*}x\end{align*}$$	$$\begin{align*}?\end{align*}$$

播放段落

The rule that matches values in a function tells you how to get from the input value to the corresponding output value. I f you do not immediately see the answer when you are trying to identify a rule, it may help to run through a checklist:
::函数中匹配值的规则指示您如何从输入值获取到相应的输出值。如果您在试图识别规则时没有立即看到答案,那么通过一个核对表可能会有帮助:

播放段落

1. Can the rule be determined by addition/ subtraction ?
::1. 规则能否通过增加/减法加以确定?

播放段落

The first input value is 1, and the first output is 9. Could the rule be "add 8?"  No, because, in the second row, if  you add 8 to 2, you'd get 10 instead of 11. This means that the rule cannot be determined by addition/subtraction alone.
::第一个输入值是 1, 第一个输出值是 9 。 规则会不会是“ 添加 8 ” ? 不, 因为, 在第二行, 如果增加 8 到 2, 你会得到 10 而不是 11 。 这意味着该规则不能单靠增加/ 减法来决定 。

播放段落

2. Can the rule be determined by multiplication/ division ?
::2. 规则能否通过乘法/区分来确定?

播放段落

The first input value is 1,  with an  output value of 9. Could the rule be "multiply by 9?"  Nope!  If you multiply 2 by 9,  you get 18 instead of 11. This means that the rule cannot be determined by multiplication/division alone.
::第一个输入值是 1, 输出值为 9. 9 。 规则能否是“ 乘以 9 ” ? 不! 如果您乘以 2乘以 9, 则得到 18 而不是 11 。 这意味着该规则不能单靠乘/ 区分来确定 。

播放段落

3. Can the rule be determined by a combination of addition/subtraction and multiplication/division?
::3. 规则能否通过加/减和倍增/区分的结合来确定?

播放段落

Try a couple of combinations of operations :  double and then add or subtract first, triple and then add or subtract second, and so on, until it becomes apparent that a combination of addition/subtraction/ and multiplication/division consistently results in the correct values throughout the table. In this case, if you double 1 and add 7, you get 9. If you double 2 and add 7, you get 11.  The rule "multiply the input by 2 and add 7" works for every value.
::尝试几组操作组合 : 双倍然后首先加或减、 三 次加或减、 二次加或减, 等等, 直到显然加/ 减/ 乘/ 乘/ division 组合一致导致整个表格的正确值。 在这种情况下, 如果您将1 和 7 加倍, 你就会得到 9 。 如果您将2 和 7 加倍, 你就会得到 11 。 规则“ 将输入乘以 2 和 7 倍 ” 对每个值都有效 。

播放段落

4. Can the rule be determined by exponents, radicals, absolute values, or another operation ?
::4. 规则能否由推手、激进分子、绝对价值或其他行动来决定?

播放段落

At this point, you know the solution to the equation so  you do not need to test for these.  
::此时此刻,你知道方程的解决方案,所以你不需要测试这些公式。