皮达哥里安神论介绍

播放段落

The Pythagorean Theorem
::毕达哥里安神话

播放段落

You  have learned how mathematicians from various cultures have advanced mathematics throughout history. In this lesson, you will start to look at how modern applied mathematicians use math. An applied mathematician uses math to solve real-world problems. While pure mathematics and applied mathematics are often thought of as being separate professions in the modern day, history has proven that this isn’t always the case. Many of the mathematicians that you have looked thus far were both pure mathematicians and applied mathematicians. Throughout the history of mathematics, you have seen many instances where a pure mathematical breakthrough needed to happen to solve a real-world problem. For example, the Greek mathematician is credited with organizing and discovering the concepts of trigonometry to predict solar eclipses. Isaac Newton is credited with inventing calculus to explain the motion of planetary bodies. While history is full of applied mathematicians, the one that you will look at in this section is Pythagoras.
::你从各种文化中了解到数学家在整个历史中是如何进化数学的。在这个教训中,你将开始观察现代应用数学家如何使用数学。一个应用数学家使用数学解决现实世界的问题。尽管在现代时代,纯数学和应用数学常常被视为是不同的职业,但历史已经证明这种情况并非始终如此。你迄今所看的许多数学家都是纯数学家和应用数学家。在整个数学史上,你已经看到许多需要实现纯数学突破才能解决现实世界问题的事例。例如,希腊数学家在组织和发现三重测量概念以预测太阳日蚀方面受到赞扬。艾萨克·牛顿被归功于发明微积分来解释行星体运动。尽管历史充满了应用数学家,但在这一节中你将看到的却是皮塔戈拉斯。

播放段落

Pythagoras of Samos (582 – 500 BCE) was an ancient Greek mathematician who founded a school in Croton southern Italy. He is credited with many discoveries including the triangle sum theorem , harmonic ratios, and most famously the Pythagorean Theorem. The Babylonians, not Pythagoras, were the first to use the ideas written in the Pythagorean Theorem but Pythagoras was the first to fully write out the theorem stating the relationship between the sides of a right triangle . Y ou will be exploring this theorem throughout this section and the following four sections. Y ou will examine how the theorem came to be and how it shaped our world.
::萨莫斯(582 - 500 BCE)的毕塔戈拉斯(Pytagoras)是一位古希腊数学家,他在意大利南部的克罗顿(Croton)创办了一所学校。 他有许多发现,包括三角方和理论、调和率,以及最著名的毕达哥伦理论。 巴比伦人,而不是毕达哥拉斯人,首先使用《毕达哥伦理论》中写的思想,但毕达哥拉斯是第一个完整地写出阐述右三角两侧之间关系的理论。你将在这一节和以下四节中探索这个理论。你将研究这些理论是如何形成的,以及它如何塑造我们的世界。

 

---

播放段落

Identifying Parts of a Right Triangle
::确定右三角部分

播放段落

The Pythagorean Theorem is stated as follows:
::《毕达哥里理论论》如下:

播放段落

The square of the hypotenuse of a right triangle is equal to the sum of the squares on the other two sides.
::右三角形的下方方等于其他两侧的平方和。

播放段落

$\begin{array}{r}{a}^2+b^2=c^2\end{array}$
::a2+b2=c2 = c2 =

播放段落
• $\begin{array}{r}a\end{array}$  and $\begin{array}{r}b\end{array}$  represent the legs of the right triangle.
  ::a和b 代表右三角形的腿。
播放段落
• $\begin{array}{r}c\end{array}$  represents the hypotenuse of the right triangle.
  ::c 表示右三角形的下限。

播放段落

Use the interactive below to label the sides of a right triangle as either being the hypotenuse or the leg.
::使用下面的交互键将右三角形的侧面标记为下方或腿。

 

 

 

 

 

---

播放段落

Solving for the Third Side of a Right Triangle
::右三角第三侧的解决

播放段落

The Pythagorean Theorem can be used in some surprising ways. However, one of the most important uses of the theorem is to find the length of the third side of a right triangle when given two side lengths. This application is used in construction and engineering on a daily basis. The set of three  integers that satisfy the Pythagorean Theorem is known as a Pythagorean Triple . Use the interactive below to practice completing a Pythagorean Triple by finding the third side of a right triangle.
::Pytagorean Theorem 可以用某些令人惊讶的方式使用。 但是, 理论的最重要用途之一是在给定两边长度时找到右三角的第三侧长度。 此应用程序每天用于建筑和工程。 符合 Pytagorean Theorem 的三根整数组被称为 Pytagorean Triple 。 使用下面的交互功能练习完成 Pytagorean Triple , 找到右三角的第三侧 。

播放段落

CK-12 PLIX Interactive: Matching Problem
::CK-12 PLIX 互动:匹配问题

 

 

 

---

播放段落

Using the Formula
::使用公式

播放段落

When using the Pythagorean Theorem to find the third side of a right triangle, you will encounter two situations: solving for the hypotenuse and solving for a leg.
::当使用毕达哥里安神话来寻找右三角形的第三面时, 你会遇到两种情况: 解决低压问题和解决一条腿问题。

播放段落

Solving for the Hypotenuse
::解决伪药问题

播放段落

Example
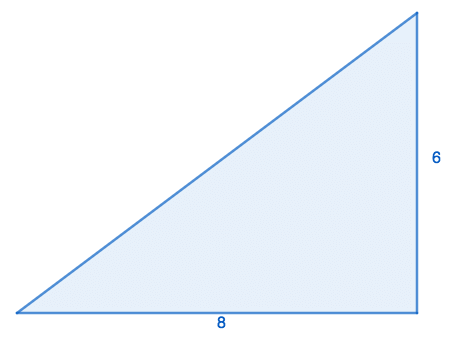
::示例示例示例示例

播放段落

Find The value of the missing side length of the right triangle below:
::查找右三角形下面缺失的侧边长度值 :

播放段落

Since the legs are interchangeable let’s say that $\begin{array}{r}a=8\end{array}$  and that $\begin{array}{r}b=6.\end{array}$   You can substitute these values into the formula and solve for $\begin{array}{r}c\end{array}$  .
::因为腿是可互换的, 所以可以说 a=8 和 b=6. 您可以将这些值替换为公式, 并解决 c 。

播放段落

$\begin{array}{r}{a}^2+b^2=c^2\\ 8^2+6^2=c^2\\ 64+36=c^2\\ 100=c^2\end{array}$
::a2+b2=c282+62=c264+36=c2100=c2

播放段落

At this point , you need to isolate the $\begin{array}{r}c\end{array}$  which means that you need to get rid of the exponent. Recall from earlier in this  lesson that the inverse operation of squared is the square root.
::在此点上, 您需要将 c 分离, 这意味着您需要摆脱引言人 。 从前面的教训中回顾到, 平方的反作用是平方根 。

播放段落

$\begin{array}{rl}\sqrt{100}& =\sqrt{c^2}\\ 10& =c\end{array}$
::100=c210=c

播放段落

Solving for the Legs
::脚脚的解决

播放段落

Example
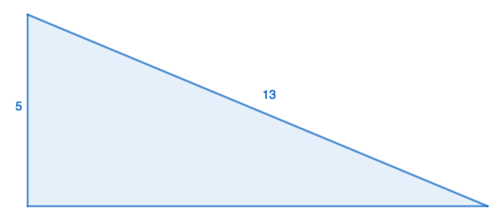
::示例示例示例示例

播放段落

Find the value of the missing side length of the right triangle below:
::查找以下右三角形边长缺失值 :

播放段落

In this case, you have one of the legs and the hypotenuse. Let’s say that $\begin{array}{r}a=5\end{array}$  and that $\begin{array}{r}c=13.\end{array}$   You can substitute these values into the formula and solve for $\begin{array}{r}b\end{array}$ .
::在此情况下, 您有一条腿和下限。 让我们假设 a=5 和 c=13 。 您可以将这些值替换为公式, 并解决 b 。

播放段落

$\begin{array}{rl}{a}^2+b^2& =c^2\\ 5^2+b^2& ={13}^2\\ 25+b^2& =169\end{array}$
::a2+b2=c252+b2=13225+b2=169

播放段落

To solve for $\begin{array}{r}b\end{array}$ , you will first need to  subtract 25  from both sides .
::要解决b,你首先需要从双方减去25。

播放段落

$\begin{array}{r}{b}^2=144\end{array}$
::b2=144(b2=144)

播放段落

At this point, you need to isolate the $\begin{array}{r}b\end{array}$  which means that you need to get rid of the exponent.  You will again use the square root to accomplish this.
::此时, 您需要将 b 分隔开来, 这意味着您需要除掉 exponent 。 您将再次使用 quare 根来完成此任务 。

播放段落

$\begin{array}{rl}\sqrt{b^2}& =\sqrt{144}\\ b& =12\end{array}$
::b2=144b=12

播放段落

There will often be situations where the missing side length represents an irrational number. In these cases, simplify or approximate the answer depending on the context of the problem.
::往往会出现缺失的侧长度代表非理性数字的情况,在这些情况下,根据问题的背景,简化或大致估计答案。

播放段落

Discussion Question
::讨论问题

播放段落

Christina claims that the answer to the previous question should also be -12 because $\begin{array}{r}-12\times -12=144.\end{array}$   Do you agree or disagree with Christina? Why?
::Christina声称,对上一个问题的答案也应该是 - 12 因为 - 1212=144。 你同意还是不同意Christina? 为什么?

 

---

播放段落

Cryptography
::加密

播放段落

One very popular area where applied mathematicians work is on data security. Over the past 30 years, the need for cybersecurity has skyrocketed. This field is known as cryptography. Mathematicians must devise unhackable ways to protect data while at the same time making it visible to those who need to see it. This process is called encryption and involves scrambling the data in an unreadable way unless you have the key. The process for encrypting data is based on a mathematical concept like prime numbers or . Only someone with the key can unscramble the information. Use the interactive below to explore this process.
::应用数学家工作的一个非常受欢迎的领域是数据安全。在过去30年中,网络安全的需求急剧增加。这个领域被称为加密。数学家必须设计出保护数据的不可破解的方法,同时让需要看到数据的人看到这些数据。这个过程被称为加密,涉及以无法读取的方式将数据剪裁,除非您有密钥。加密数据的过程基于像质数或.只有钥匙的人才能解密信息。使用下面的交互程序来探索这个过程。

播放段落

CK-12 PLIX Interactive: Cryptography
::CK-12 PLIX 互动:加密

 

Summary

播放段落 The Pythagorean Theorem states that $\begin{array}{r}{a}^2+b^2=c^2.\end{array}$   ::《毕达哥里人理论论》指出,a2+b2=c2。 播放段落 Use the equation for the pythagorean theorem to find a missing side length of a triangle given the measures of two of the side lengths. ::使用地平线定理方程式的方程式来找到一个三角形缺失的侧长, 因为边距的度量为两个。