其他有趣的发行版(Other Interesting Distributions)
章节大纲
-
首先,代码使用
sklearn.datasets.make_moons函数生成了一个“月亮”形状的二维数据集:Pythonimport numpy as np import sklearn.datasets as ds data, labels = ds.make_moons(n_samples=150, shuffle=True, noise=0.19, random_state=None)-
n_samples=150:生成150个数据点。 -
shuffle=True:打乱数据。 -
noise=0.19:数据中加入的噪声量。
接下来,对数据进行了平移,使得第一个特征(X轴)的最小值变为0:
Pythondata += np.array([-np.ndarray.min(data[:,0]), -np.ndarray.min(data[:,1])]) np.ndarray.min(data[:,0]), np.ndarray.min(data[:,1]) # 输出: (0.0, 0.34649342272719386)这确保了数据集的某个特定坐标轴的起始点。
然后,使用
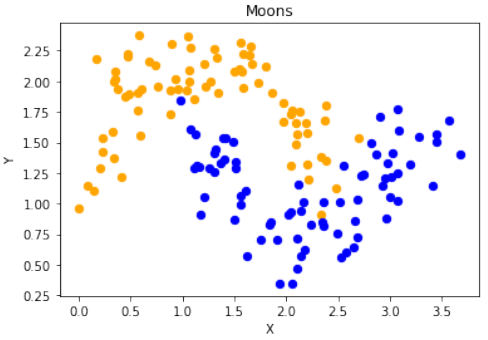
matplotlib.pyplot将生成的数据可视化:Pythonimport matplotlib.pyplot as plt fig, ax = plt.subplots() ax.scatter(data[labels==0, 0], data[labels==0, 1], c='orange', s=40, label='oranges') ax.scatter(data[labels==1, 0], data[labels==1, 1], c='blue', s=40, label='blues') ax.set(xlabel='X', ylabel='Y', title='Moons') #ax.legend(loc='upper right');-
将
labels为0的数据点标记为橙色,labels为1的数据点标记为蓝色。 -
设置了X轴、Y轴标签和图表标题。
数据缩放
接着,文本介绍了一个将数据从一个范围 [min,max] 缩放到另一个范围 [a,b] 的公式:
这个公式用于将数据点的X和Y坐标转换到新的范围:
Pythonmin_x_new, max_x_new = 33, 88 min_y_new, max_y_new = 12, 20 data, labels = ds.make_moons(n_samples=100, shuffle=True, noise=0.05, random_state=None) min_x, min_y = np.ndarray.min(data[:,0]), np.ndarray.min(data[:,1]) max_x, max_y = np.ndarray.max(data[:,0]), np.ndarray.max(data[:,1]) data -= np.array([min_x, min_y]) # 1. 平移数据,使最小值变为0 data *= np.array([(max_x_new - min_x_new) / (max_x - min_x), (max_y_new - min_y_new) / (max_y - min_y)]) # 2. 缩放数据到新范围的比例 data += np.array([min_x_new, min_y_new]) # 3. 平移数据到新范围的最小值 # 输出转换后的前6个数据点: # Output:array([[71.14479608, 12.28919998], ...])这一系列操作实现了数据的最小-最大归一化。
scale_data函数为了方便地进行数据缩放,定义了一个
scale_data函数:Pythondef scale_data(data, new_limits, inplace=False): if not inplace: data = data.copy() # 如果inplace为False,则复制数据,避免修改原始数据 min_x, min_y = np.ndarray.min(data[:,0]), np.ndarray.min(data[:,1]) max_x, max_y = np.ndarray.max(data[:,0]), np.ndarray.max(data[:,1]) min_x_new, max_x_new = new_limits[0] min_y_new, max_y_new = new_limits[1] data -= np.array([min_x, min_y]) data *= np.array([(max_x_new - min_x_new) / (max_x - min_x), (max_y_new - min_y_new) / (max_y - min_y)]) data += np.array([min_x_new, min_y_new]) if inplace: return None # 如果inplace为True,直接修改传入的数据,返回None else: return data # 否则返回缩放后的新数据该函数接受数据、新的范围
new_limits和一个inplace参数。如果inplace为True,则直接修改原始数据;否则返回一个缩放后的新副本。接着,使用这个函数对“月亮”数据集进行缩放并可视化:
Pythondata, labels = ds.make_moons(n_samples=100, shuffle=True, noise=0.05, random_state=None) scale_data(data, [(1, 4), (3, 8)], inplace=True) # 将数据缩放到 X 轴范围 [1, 4] 和 Y 轴范围 [3, 8] # 输出缩放后的前10个数据点: # Output:array([[1.19312571, 6.70797983], ...]) fig, ax = plt.subplots() ax.scatter(data[labels==0, 0], data[labels==0, 1], c='orange', s=40, label='oranges') ax.scatter(data[labels==1, 0], data[labels==1, 1], c='blue', s=40, label='blues') ax.set(xlabel='X', ylabel='Y', title='moons') ax.legend(loc='upper right');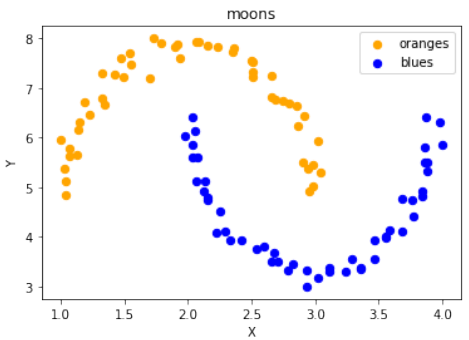
Circles 数据集可视化
代码随后展示了如何生成和可视化“圆形”数据集:
Pythonimport sklearn.datasets as ds data, labels = ds.make_circles(n_samples=100, shuffle=True, noise=0.05, random_state=None) fig, ax = plt.subplots() ax.scatter(data[labels==0, 0], data[labels==0, 1], c='orange', s=40, label='oranges') ax.scatter(data[labels==1, 0], data[labels==1, 1], c='blue', s=40, label='blues') ax.set(xlabel='X', ylabel='Y', title='circles') ax.legend(loc='upper right')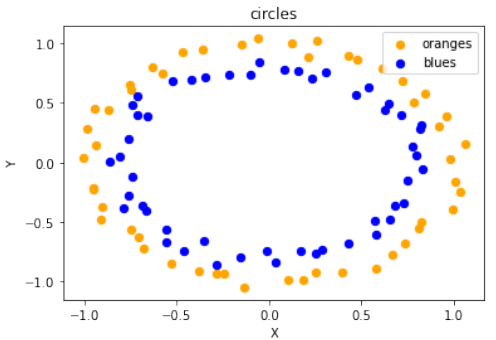
不同类型的分类数据集
接下来,代码演示了
sklearn.datasets中其他用于生成分类数据集的函数,并进行可视化:Pythonimport matplotlib.pyplot as plt from sklearn.datasets import make_classification, make_blobs, make_gaussian_quantiles plt.figure(figsize=(8, 8)) plt.subplots_adjust(bottom=.05, top=.9, left=.05, right=.95) # 1. 两个特征,一个信息性特征,每个类别一个簇 plt.subplot(321) plt.title("One informative feature, one cluster per class", fontsize='small') X1, Y1 = make_classification(n_features=2, n_redundant=0, n_informative=1, n_clusters_per_class=1) plt.scatter(X1[:, 0], X1[:, 1], marker='o', c=Y1, s=25, edgecolor='k') # 2. 两个特征,两个信息性特征,每个类别一个簇 plt.subplot(322) plt.title("Two informative features, one cluster per class", fontsize='small') X1, Y1 = make_classification(n_features=2, n_redundant=0, n_informative=2, n_clusters_per_class=1) plt.scatter(X1[:, 0], X1[:, 1], marker='o', c=Y1, s=25, edgecolor='k') # 3. 两个特征,两个信息性特征,每个类别两个簇 plt.subplot(323) plt.title("Two informative features, two clusters per class", fontsize='small') X2, Y2 = make_classification(n_features=2, n_redundant=0, n_informative=2) plt.scatter(X2[:, 0], X2[:, 1], marker='o', c=Y2, s=25, edgecolor='k') # 4. 多类别,两个信息性特征,一个簇 plt.subplot(324) plt.title("Multi-class, two informative features, one cluster", fontsize='small') X1, Y1 = make_classification(n_features=2, n_redundant=0, n_informative=2, n_clusters_per_class=1, n_classes=3) plt.scatter(X1[:, 0], X1[:, 1], marker='o', c=Y1, s=25, edgecolor='k') # 5. 高斯分布分为三个分位数 plt.subplot(325) plt.title("Gaussian divided into three quantiles", fontsize='small') X1, Y1 = make_gaussian_quantiles(n_features=2, n_classes=3) plt.scatter(X1[:, 0], X1[:, 1], marker='o', c=Y1, s=25, edgecolor='k') plt.show()这部分代码展示了
make_classification和make_gaussian_quantiles如何生成不同复杂度、不同类别数量和不同特征结构的数据集,用于机器学习任务的测试。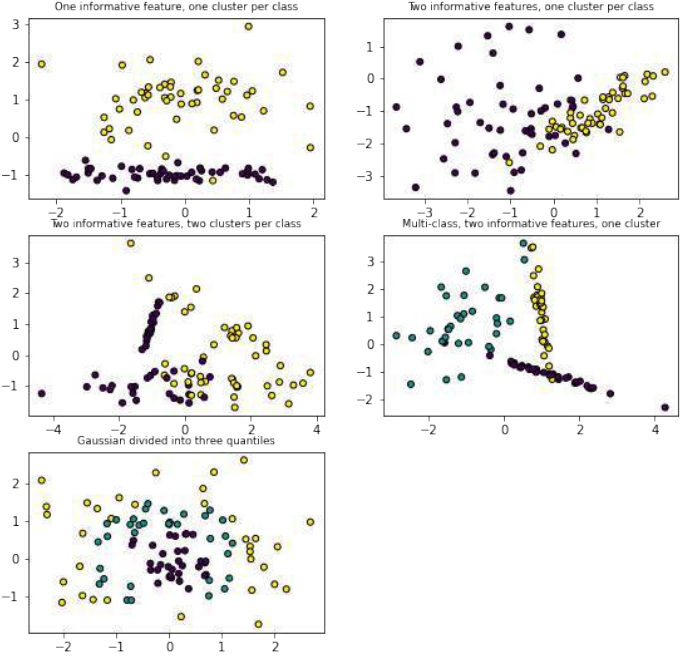
练习
这部分提出了三个练习,要求用户创建满足特定条件的数据集。
练习 1
创建一个可以被感知机(不带偏置节点)分离的两个测试集。
感知机不带偏置节点意味着决策边界必须通过原点。
练习 2
创建两个不能被通过原点的分割线分离的测试集。
练习 3
创建一个包含“Tiger”、“Lion”、“Penguin”、“Dolphin”和“Python”五个类别的数据集,其分布类似于给定的图示。
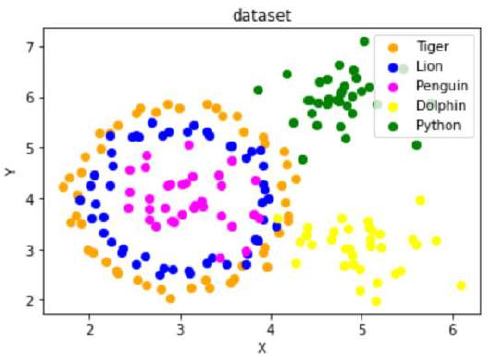
练习解答
这部分提供了上述练习的解决方案。
练习 1 解决方案
使用
make_blobs创建两个簇,它们分别位于相对的象限,使得通过原点的直线可以将其分离:Pythonfrom sklearn.datasets import make_blobs data, labels = make_blobs(n_samples=100, cluster_std = 0.5, centers=[[1, 4] ,[4, 1]], random_state=1) # 簇中心设置为 [1, 4] 和 [4, 1],这样一条穿过原点的线可以分隔它们。 fig, ax = plt.subplots() colours = ["orange", "green"] label_name = ["Tigers", "Lions"] for label in range(0, 2): ax.scatter(data[labels==label, 0], data[labels==label, 1], c=colours[label], s=40, label=label_name[label]) ax.set(xlabel='X', ylabel='Y', title='dataset') ax.legend(loc='upper right')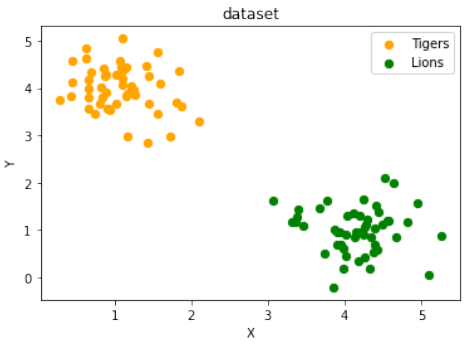
练习 2 解决方案
创建两个不能被通过原点的分割线分离的簇。例如,将两个簇都放置在同一个象限,或者一个簇围绕原点,另一个在外部。这里的解决方案是将两个簇放置在第一象限:
Pythonfrom sklearn.datasets import make_blobs data, labels = make_blobs(n_samples=100, cluster_std = 0.5, centers=[[2, 2] ,[4, 4]], random_state=1) # 簇中心设置为 [2, 2] 和 [4, 4],都在第一象限,无法被通过原点的线分离。 fig, ax = plt.subplots() colours = ["orange", "green"] label_name = ["label0", "label1"] for label in range(0, 2): ax.scatter(data[labels==label, 0], data[labels==label, 1], c=colours[label], s=40, label=label_name[label]) ax.set(xlabel='X', ylabel='Y', title='dataset') ax.legend(loc='upper right')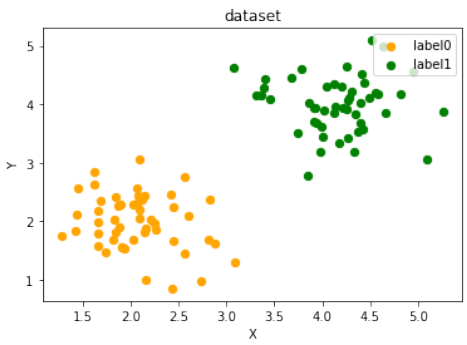
练习 3 解决方案
结合
make_circles和make_blobs来创建五个类别的数据集,模拟复杂的分布:Pythonimport sklearn.datasets as ds from sklearn.datasets import make_blobs import numpy as np # 生成第一个圆形数据集 (作为两个类别) data, labels = ds.make_circles(n_samples=100, shuffle=True, noise=0.05, random_state=42) # 生成第二个 blob 数据集 (作为三个类别) centers = [[3, 4], [5, 3], [4.5, 6]] data2, labels2 = make_blobs(n_samples=100, cluster_std = 0.5, centers=centers, random_state=1) # 调整 labels2 的标签,使其与 labels 不重叠,从2开始 for i in range(len(centers)-1, -1, -1): labels2[labels2==0+i] = i+2 # print(labels2) # 输出调整后的 labels2 数组 # 合并两个数据集的标签 labels = np.concatenate([labels, labels2]) # 对第一个圆形数据集进行缩放和平移,使其与 blob 数据集结合时位置合适 data = data * [1.2, 1.8] + [3, 4] # 合并两个数据集的数据 data = np.concatenate([data, data2], axis=0) fig, ax = plt.subplots() colours = ["orange", "blue", "magenta", "yellow", "green"] label_name = ["Tiger", "Lion", "Penguin", "Dolphin", "Python"] for label in range(0, len(centers)+2): # 遍历所有5个类别 ax.scatter(data[labels==label, 0], data[labels==label, 1], c=colours[label], s=40, label=label_name[label]) ax.set(xlabel='X', ylabel='Y', title='dataset') ax.legend(loc='upper right')这个解决方案通过
make_circles创建了内外的两个圈,然后通过make_blobs创建了三个离散的簇,并将它们合并在一起,形成了五个不同类别的数据集。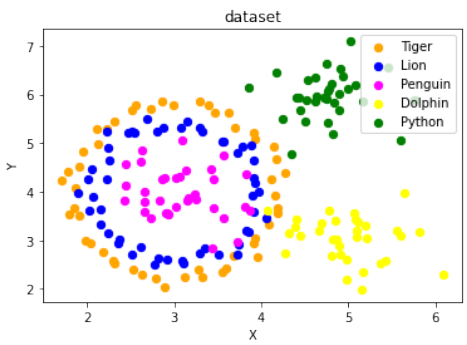
import numpy as np
import sklearn.datasets as ds
data, labels = ds.make_moons(n_samples=150,
shuffle=True,
noise=0.19,
random_state=None)
data += np.array(-np.ndarray.min(data[:,0]),
-np.ndarray.min(data[:,1]))
np.ndarray.min(data[:,0]), np.ndarray.min(data[:,1])
Output0.0, 0.34649342272719386)
import matplotlib.pyplot as plt
fig, ax = plt.subplots()
ax.scatter(data[labels==0, 0], data[labels==0, 1],
c='orange', s=40, label='oranges')
ax.scatter(data[labels==1, 0], data[labels==1, 1],
c='blue', s=40, label='blues')
ax.set(xlabel='X',
ylabel='Y',
title='Moons')
#ax.legend(loc='upper right');
54
Output:[Text(0.5, 0, 'X'), Text(0, 0.5, 'Y'), Text(0.5, 1.0, 'Moon
s')]
We want to scale values that are in a range [min, max] in a range [a, b] .
(b − a) ⋅ (x − min)
f(x) =
+ a
max − min
We now use this formula to transform both the X and Y coordinates of data into other ranges:
min_x_new, max_x_new = 33, 88
min_y_new, max_y_new = 12, 20
data, labels = ds.make_moons(n_samples=100,
shuffle=True,
noise=0.05,
random_state=None)
min_x, min_y = np.ndarray.min(data[:,0]), np.ndarray.min(dat
a[:,1])
max_x, max_y = np.ndarray.max(data[:,0]), np.ndarray.max(dat
a[:,1])
#data -= np.array([min_x, 0])
#data *= np.array([(max_x_new - min_x_new) / (max_x - min_x), 1])
#data += np.array([min_x_new, 0])
#data -= np.array([0, min_y])
#data *= np.array([1, (max_y_new - min_y_new) / (max_y - min_y)])
55
#data += np.array([0, min_y_new])
data -= np.array([min_x, min_y])
data *= np.array([(max_x_new - min_x_new) / (max_x - min_x), (ma
x_y_new - min_y_new) / (max_y - min_y)])
data += np.array([min_x_new, min_y_new])
#np.ndarray.min(data[:,0]), np.ndarray.max(data[:,0])
data[:6]
Output:array([[71.14479608, 12.28919998],
[62.16584307, 18.75442981],
[61.02613211, 12.80794358],
[64.30752046, 12.32563839],
[81.41469127, 13.64613406],
[82.03929032, 13.63156545]])
def scale_data(data, new_limits, inplace=False ):
if not inplace:
data = data.copy()
min_x, min_y = np.ndarray.min(data[:,0]), np.ndarray.min(dat
a[:,1])
max_x, max_y = np.ndarray.max(data[:,0]), np.ndarray.max(dat
a[:,1])
min_x_new, max_x_new = new_limits[0]
min_y_new, max_y_new = new_limits[1]
data -= np.array([min_x, min_y])
data *= np.array([(max_x_new - min_x_new) / (max_x - min_x),
(max_y_new - min_y_new) / (max_y - min_y)])
data += np.array([min_x_new, min_y_new])
if inplace:
return None
else:
return data
data, labels = ds.make_moons(n_samples=100,
shuffle=True,
noise=0.05,
random_state=None)
scale_data(data, [(1, 4), (3, 8)], inplace=True)
56
data[:10]
Output:array([[1.19312571, 6.70797983],
[2.74306138, 6.74830445],
[1.15255757, 6.31893824],
[1.03927303, 4.83714182],
[2.91313352, 6.44139267],
[2.13227292, 5.120716 ],
[2.65590196, 3.49417953],
[2.98349928, 5.02232383],
[3.35660593, 3.34679462],
[2.15813861, 4.8036458 ]])
fig, ax = plt.subplots()
ax.scatter(data[labels==0, 0], data[labels==0, 1],
c='orange', s=40, label='oranges')
ax.scatter(data[labels==1, 0], data[labels==1, 1],
c='blue', s=40, label='blues')
ax.set(xlabel='X',
ylabel='Y',
title='moons')
ax.legend(loc='upper right');
import sklearn.datasets as ds
data, labels = ds.make_circles(n_samples=100,
shuffle=True,
57
fig, ax = plt.subplots()
noise=0.05,
random_state=None)
ax.scatter(data[labels==0, 0], data[labels==0, 1],
c='orange', s=40, label='oranges')
ax.scatter(data[labels==1, 0], data[labels==1, 1],
c='blue', s=40, label='blues')
ax.set(xlabel='X',
ylabel='Y',
title='circles')
ax.legend(loc='upper right')
Output:<matplotlib.legend.Legend at 0x7f54588c2e20>
print(__doc__)
import matplotlib.pyplot as plt
from sklearn.datasets import make_classification
from sklearn.datasets import make_blobs
from sklearn.datasets import make_gaussian_quantiles
plt.figure(figsize=(8, 8))
plt.subplots_adjust(bottom=.05, top=.9, left=.05, right=.95)
58
plt.subplot(321)
plt.title("One informative feature, one cluster per class", fontsi
ze='small')
X1, Y1 = make_classification(n_features=2, n_redundant=0, n_inform
ative=1,
n_clusters_per_class=1)
plt.scatter(X1[:, 0], X1[:, 1], marker='o', c=Y1,
s=25, edgecolor='k')
plt.subplot(322)
plt.title("Two informative features, one cluster per class", fonts
ize='small')
X1, Y1 = make_classification(n_features=2, n_redundant=0, n_inform
ative=2,
n_clusters_per_class=1)
plt.scatter(X1[:, 0], X1[:, 1], marker='o', c=Y1,
s=25, edgecolor='k')
plt.subplot(323)
plt.title("Two informative features, two clusters per class",
fontsize='small')
X2, Y2 = make_classification(n_features=2,
n_redundant=0,
n_informative=2)
plt.scatter(X2[:, 0], X2[:, 1], marker='o', c=Y2,
s=25, edgecolor='k')
plt.subplot(324)
plt.title("Multi-class, two informative features, one cluster",
fontsize='small')
X1, Y1 = make_classification(n_features=2,
n_redundant=0,
n_informative=2,
n_clusters_per_class=1,
n_classes=3)
plt.scatter(X1[:, 0], X1[:, 1], marker='o', c=Y1,
s=25, edgecolor='k')
plt.subplot(325)
plt.title("Gaussian divided into three quantiles", fontsize='smal
l')
X1, Y1 = make_gaussian_quantiles(n_features=2, n_classes=3)
plt.scatter(X1[:, 0], X1[:, 1], marker='o', c=Y1,
s=25, edgecolor='k')
59
plt.show()
Automatically created module for IPython interactive environment
EXERCISES
EXERCISE 1
Create two testsets which are separable with a perceptron without a bias node.
EXERCISE 2
Create two testsets which are not separable with a dividing line going through the origin.
60
EXERCISE 3
Create a dataset with five classes "Tiger", "Lion", "Penguin", "Dolphin", and "Python". The sets should look
similar to the following diagram:
SOLUTIONS
SOLUTION TO EXERCISE 1
data, labels = make_blobs(n_samples=100,
cluster_std = 0.5,
centers=[[1, 4] ,[4, 1]],
random_state=1)
fig, ax = plt.subplots()
colours = ["orange", "green"]
label_name = ["Tigers", "Lions"]
for label in range(0, 2):
ax.scatter(data[labels==label, 0], data[labels==label, 1],
c=colours[label], s=40, label=label_name[label])
ax.set(xlabel='X',
ylabel='Y',
title='dataset')
61
ax.legend(loc='upper right')
Output:<matplotlib.legend.Legend at 0x7f788afb2c40>
SOLUTION TO EXERCISE 2
data, labels = make_blobs(n_samples=100,
cluster_std = 0.5,
centers=[[2, 2] ,[4, 4]],
random_state=1)
fig, ax = plt.subplots()
colours = ["orange", "green"]
label_name = ["label0", "label1"]
for label in range(0, 2):
ax.scatter(data[labels==label, 0], data[labels==label, 1],
c=colours[label], s=40, label=label_name[label])
ax.set(xlabel='X',
ylabel='Y',
title='dataset')
ax.legend(loc='upper right')
62
Output:<matplotlib.legend.Legend at 0x7f788af8eac0>
SOLUTION TO EXERCISE 3
import sklearn.datasets as ds
data, labels = ds.make_circles(n_samples=100,
shuffle=True,
noise=0.05,
random_state=42)
centers = [[3, 4], [5, 3], [4.5, 6]]
data2, labels2 = make_blobs(n_samples=100,
cluster_std = 0.5,
centers=centers,
random_state=1)
for i in range(len(centers)-1, -1, -1):
labels2[labels2==0+i] = i+2
print(labels2)
labels = np.concatenate([labels, labels2])
data = data * [1.2, 1.8] + [3, 4]
data = np.concatenate([data, data2], axis=0)
63
[2 4 4 3 4 4 3 3 2 4 4 2 4 4 3 4 2 4 4 4 4 2 2 4 4 3 2 2 3 2 2 3
2 3 3 3 3
3 4 3 3 2 3 3 3 2 2 2 2 3 4 4 4 2 4 3 3 2 2 3 4 4 3 3 4 2 4 2 4
3 3 4 2 2
3 4 4 2 3 2 3 3 4 2 2 2 2 3 2 4 2 2 3 3 4 4 2 2 4 3]
fig, ax = plt.subplots()
colours = ["orange", "blue", "magenta", "yellow", "green"]
label_name = ["Tiger", "Lion", "Penguin", "Dolphin", "Python"]
for label in range(0, len(centers)+2):
ax.scatter(data[labels==label, 0], data[labels==label, 1],
c=colours[label], s=40, label=label_name[label])
ax.set(xlabel='X',
ylabel='Y',
title='dataset')
ax.legend(loc='upper right')
Output:<matplotlib.legend.Legend at 0x7f788b1d42b0> -