混淆矩阵(Confusion Matrix)
章节大纲
-
介绍
在我们之前的机器学习教程章节(《使用 Python 和 Numpy 的神经网络》 和 《从零开始的神经网络》)中,我们实现了各种算法,但没有适当地衡量输出的质量。主要原因是,我们使用了非常简单和小型的数据集进行学习和测试。在《神经网络:MNIST 测试》这一章中,我们将使用大型数据集和十个类别,因此我们需要合适的评估工具。在本章中,我们将介绍混淆矩阵的概念:
混淆矩阵是一个矩阵(表格),可用于衡量机器学习算法(通常是监督学习算法)的性能。混淆矩阵的每一行代表实际类别的实例,每一列代表预测类别的实例。在本教程的这一章中,我们保持这种方式,但也可以反过来,即行表示预测类别,列表示实际类别。混淆矩阵这个名称反映了一个事实,即它使我们很容易看到分类算法中发生了哪些混淆。例如,算法本应将样本预测为 c_i,因为实际类别是 c_i,但算法却输出 c_j。在这种错误标记的情况下,当构建混淆矩阵时,元素 cm[i,j] 将加一。
我们将在下面的类中定义计算混淆矩阵、精确率 (precision) 和召回率 (recall) 的方法。
两类情况
在两类情况下,即“负类”和“正类”,混淆矩阵可能看起来像这样:
实际
预测
负类
正类
负类
11
0
正类
1
12
矩阵的字段含义如下:
实际
预测
负类
正类
负类
TN
FP
真负类
假正类
正类
FN
TP
假负类
真正类
我们现在可以定义一些机器学习中使用的重要性能指标:
准确率 (Accuracy):
\(AC=\frac{TN+TP}{TN+FP+FN+TP}\)
准确率并不总是衡量性能的足够指标。假设我们有 1000 个样本。其中 995 个是负例,5 个是正例。让我们进一步假设我们有一个分类器,无论它遇到什么,都将其分类为负例。准确率将达到惊人的 99.5%,尽管该分类器未能识别任何正例。
召回率 (Recall),又称真阳性率 (True Positive Rate):
\(recall=\frac{TP}{FN+TP}\)
真负性率 (True Negative Rate):
\(TNR=\frac{TN}{TN+FP}\)
精确率 (Precision):
\(precision=\frac{TP}{FP+TP}\)
多类情况
为了衡量机器学习算法的结果,之前的混淆矩阵将不足够。我们需要将其推广到多类情况。
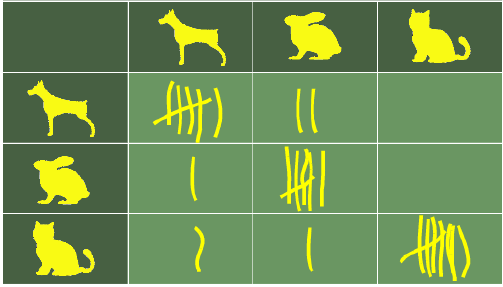
假设我们有 25 只动物的样本,例如 7 只猫、8 只狗和 10 条蛇(很可能是蟒蛇)。我们的识别算法的混淆矩阵可能如下表所示:
实际
预测
狗
猫
蛇
狗
6
2
0
猫
1
6
0
蛇
1
1
8
在这个混淆矩阵中,系统正确预测了八只实际狗中的六只,但在两种情况下它把狗当作了猫。七只实际猫中有六只被正确识别,但在一种情况下猫被当作了狗。通常,很难把蛇当作狗或猫,但我们的分类器在两种情况下却发生了这种情况。然而,十条蛇中有八条被正确识别。(这个机器学习算法很可能不是用 Python 程序编写的,因为 Python 应该能够正确识别自己的物种
)
你可以看到所有正确预测都位于表格的对角线上,因此预测错误可以很容易地在表格中找到,因为它们将由对角线以外的值表示。
我们可以将其推广到多类情况。为此,我们对混淆矩阵的行和列进行总结。鉴于矩阵如上所示,即矩阵的给定行对应于“真实值”的特定值,我们有:
\(Precision_i=\frac{M_ii}{\sum_{j} M_ji}\)
\(Recall_i=\frac{M_ii}{sum_{j} M_ij}\)
这意味着,精确率是算法正确预测类别 i 的情况占所有算法预测 i 的实例(正确和不正确)的比例。另一方面,召回率是算法正确预测 i 的情况占所有标记为 i 的情况的比例。
让我们将其应用于我们的例子:
我们动物的精确率可以计算为:
\(precision_{dogs}=6/(6+1+1)=3/4=0.75\)
\(precision_{cats}=6/(2+6+1)=6/9=0.67\)
\(precision_{snakes}=8/(0+0+8)=1\)
召回率这样计算:
\(recall_{dogs}=6/(6+2+0)=3/4=0.75\)
\(recall_{cats}=6/(1+6+0)=6/7=0.86\)
\(recall_{snakes}=8/(1+1+8)=4/5=0.8\)
示例
我们现在准备用 Python 编写代码。以下代码显示了一个多类机器学习问题的混淆矩阵,该问题有十个标签,例如用于识别手写数字的算法。
如果您不熟悉 Numpy 和 Numpy 数组,我们推荐您阅读我们的 Numpy 教程。
Pythonimport numpy as np cm = np.array( [[5825, 1, 49, 23, 7, 46, 30, 12, 21, 26], [ 1, 6654, 48, 25, 10, 32, 19, 62, 111, 10], [ 2, 20, 5561, 69, 13, 10, 2, 45, 18, 2], [ 6, 26, 99, 5786, 5, 111, 1, 41, 110, 79], [ 4, 10, 43, 6, 5533, 32, 11, 53, 34, 79], [ 3, 1, 2, 56, 0, 4954, 23, 0, 12, 5], [ 31, 4, 42, 22, 45, 103, 5806, 3, 34, 3], [ 0, 4, 30, 29, 5, 6, 0, 5817, 2, 28], [ 35, 6, 63, 58, 8, 59, 26, 13, 5394, 24], [ 16, 16, 21, 57, 216, 68, 0, 219, 115, 5693]]) # 'precision' 和 'recall' 函数计算单个标签的值,而 'precision_macro_average' 计算整个分类问题的精确率。 def precision(label, confusion_matrix): col = confusion_matrix[:, label] return confusion_matrix[label, label] / col.sum() def recall(label, confusion_matrix): row = confusion_matrix[label, :] return confusion_matrix[label, label] / row.sum() def precision_macro_average(confusion_matrix): rows, columns = confusion_matrix.shape sum_of_precisions = 0 for label in range(rows): sum_of_precisions += precision(label, confusion_matrix) return sum_of_precisions / rows def recall_macro_average(confusion_matrix): rows, columns = confusion_matrix.shape sum_of_recalls = 0 for label in range(columns): sum_of_recalls += recall(label, confusion_matrix) return sum_of_recalls / columns print("label precision recall") for label in range(10): print(f"{label:5d} {precision(label, cm):<span class="hljs-number">9.3</span>f} {recall(label, cm):<span class="hljs-number">6.3</span>f}") print("precision total:", precision_macro_average(cm)) print("recall total:", recall_macro_average(cm)) def accuracy(confusion_matrix): diagonal_sum = confusion_matrix.trace() # 对角线元素之和(正确预测) sum_of_all_elements = confusion_matrix.sum() # 所有元素之和(总样本数) return diagonal_sum / sum_of_all_elements print("accuracy:", accuracy(cm))输出:
label precision recall 0 0.983 0.964 1 0.987 0.954 2 0.933 0.968 3 0.944 0.924 4 0.947 0.953 5 0.914 0.980 6 0.981 0.953 7 0.928 0.982 8 0.922 0.949 9 0.957 0.887 precision total: 0.949688556405 recall total: 0.951453154788 accuracy: 0.95038333333333336
In the previous chapters of our Machine
Learning tutorial (Neural Networks with
Python and Numpy and Neural Networks
from Scratch ) we implemented various
algorithms, but we didn't properly
measure the quality of the output. The
main reason was that we used very simple
and small datasets to learn and test. In the
chapter Neural Network: Testing with
MNIST, we will work with large datasets
and ten classes, so we need proper
evaluations tools. We will introduce in
this chapter the concepts of the confusion
matrix:
A confusion matrix is a matrix (table) that can be used to measure the performance of an machine learning
algorithm, usually a supervised learning one. Each row of the confusion matrix represents the instances of an
actual class and each column represents the instances of a predicted class. This is the way we keep it in this
chapter of our tutorial, but it can be the other way around as well, i.e. rows for predicted classes and columns
for actual classes. The name confusion matrix reflects the fact that it makes it easy for us to see what kind of
confusions occur in our classification algorithms. For example the algorithms should have predicted a sample
as c i because the actual class is c i, but the algorithm came out with cj. In this case of mislabelling the element
cm[i, j] will be incremented by one, when the confusion matrix is constructed.
We will define methods to calculate the confusion matrix, precision and recall in the following class.
2-CLASS CASE
In a 2-class case, i.e. "negative" and "positive", the confusion matrix may look like this:
predicted
actual
negative
positive
negative
11
0
positive
1
12
192
The fields of the matrix mean the following:
predicted
actual
negative
positive
negative
TN
FP
True positive
False Positive
positive
FN
TP
False negative
True positive
We can define now some important performance measures used in machine learning:
Accuracy:
TN + TP
AC =
TN + FP + FN + TP
The accuracy is not always an adequate performance measure. Let us assume we have 1000 samples. 995 of
these are negative and 5 are positive cases. Let us further assume we have a classifier, which classifies
whatever it will be presented as negative. The accuracy will be a surprising 99.5%, even though the classifier
could not recognize any positive samples.
Recall aka. True Positive Rate:
TP
recall =
FN + TP
True Negative Rate:
FP
TNR =
TN + FP
Precision:
TP
precision :
FP + TP
193
MULTI-CLASS CASE
To measure the results of machine learning algorithms, the previous confusion matrix will not be sufficient.
We will need a generalization for the multi-class case.
Let us assume that we have a sample of 25 animals, e.g. 7 cats, 8 dogs, and 10 snakes, most probably Python
snakes. The confusion matrix of our recognition algorithm may look like the following table:
predicted
actual
dog
cat
snake
dog
6
2
0
cat
1
6
0
snake
1
1
8
In this confusion matrix, the system correctly predicted six of the eight actual dogs, but in two cases it took a
dog for a cat. The seven acutal cats were correctly recognized in six cases but in one case a cat was taken to be
a dog. Usually, it is hard to take a snake for a dog or a cat, but this is what happened to our classifier in two
cases. Yet, eight out of ten snakes had been correctly recognized. (Most probably this machine learning
algorithm was not written in a Python program, because Python should properly recognize its own species)
You can see that all correct predictions are located in the diagonal of the table, so prediction errors can be
easily found in the table, as they will be represented by values outside the diagonal.
We can generalize this to the multi-class case. To do this we summarize over the rows and columns of the
confusion matrix. Given that the matrix is oriented as above, i.e., that a given row of the matrix corresponds to
specific value for the "truth", we have:
Precision i =
M ii
∑ jMji
Mii
Recalli =
∑jM ij
This means, precision is the fraction of cases where the algorithm correctly predicted class i out of all
instances where the algorithm predicted i (correctly and incorrectly). recall on the other hand is the fraction of
cases where the algorithm correctly predicted i out of all of the cases which are labelled as i.
Let us apply this to our example:
194
The precision for our animals can be calculated as
precisiondogs = 6 / (6 + 1 + 1) = 3 / 4 = 0.75
precision = 6 / (2 + 6 + 1) = 6 / 9 = 0.67
catsprecision snakes = 8 / (0 + 0 + 8) = 1
The recall is calculated like this:
recall = 6 / (6 + 2 + 0) = 3 / 4 = 0.75
dogsrecall cats = 6 / (1 + 6 + 0) = 6 / 7 = 0.86
recall = 8 / (1 + 1 + 8) = 4 / 5 = 0.8
snakesEXAMPLE
We are ready now to code this into Python. The following code shows a confusion matrix for a multi-class
machine learning problem with ten labels, so for example an algorithms for recognizing the ten digits from
handwritten characters.
If you are not familiar with Numpy and Numpy arrays, we recommend our tutorial on Numpy.
import numpy as np
cm = np.array(
[[5825,
1,
49,
23,
7,
46,
30,
12,
21,
26],
[
1, 6654,
48,
25,
10,
32,
19,
62, 111,
10],
[
2,
20, 5561,
69,
13,
10,
2,
45,
18,
2],
[
6,
26,
99, 5786,
5, 111,
1,
41, 110,
79],
[
4,
10,
43,
6, 5533,
32,
11,
53,
34,
79],
[
3,
1,
2,
56,
0, 4954,
23,
0,
12,
5],
[ 31,
4,
42,
22,
45, 103, 5806,
3,
34,
3],
[
0,
4,
30,
29,
5,
6,
0, 5817,
2,
28],
[ 35,
6,
63,
58,
8,
59,
26,
13, 5394,
24],
[ 16,
16,
21,
57, 216,
68,
0, 219, 115, 5693]])
The functions 'precision' and 'recall' calculate values for a label, whereas the function
'precision_macro_average' the precision for the whole classification problem calculates.
def precision(label, confusion_matrix):
col = confusion_matrix[:, label]
return confusion_matrix[label, label] / col.sum()
195
def recall(label, confusion_matrix):
row = confusion_matrix[label, :]
return confusion_matrix[label, label] / row.sum()
def precision_macro_average(confusion_matrix):
rows, columns = confusion_matrix.shape
sum_of_precisions = 0
for label in range(rows):
sum_of_precisions += precision(label, confusion_matrix)
return sum_of_precisions / rows
def recall_macro_average(confusion_matrix):
rows, columns = confusion_matrix.shape
sum_of_recalls = 0
for label in range(columns):
sum_of_recalls += recall(label, confusion_matrix)
return sum_of_recalls / columns
print("label precision recall")
for label in range(10):
print(f"{label:5d} {precision(label, cm):9.3f} {recall(label,<br>cm):6.3f}")
label precision recall
0
0.983 0.964
1
0.987 0.954
2
0.933 0.968
3
0.944 0.924
4
0.947 0.953
5
0.914 0.980
6
0.981 0.953
7
0.928 0.982
8
0.922 0.949
9
0.957 0.887
print("precision total:", precision_macro_average(cm))
print("recall total:", recall_macro_average(cm))
precision total: 0.949688556405
recall total: 0.951453154788
def accuracy(confusion_matrix):
diagonal_sum = confusion_matrix.trace()
sum_of_all_elements = confusion_matrix.sum()
196
return diagonal_sum / sum_of_all_elements
accuracy(cm)
Output:0.95038333333333336