Section: 十进制乘法的面积模型 | 4.8十进制乘法的面积模型

Section outline

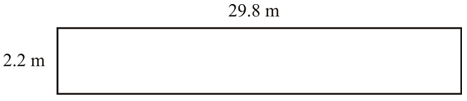
Kevin needs to figure out the area of a room. This would normally be a simple project, except that the dimensions have decimals. The length of the room is 9.5 feet. The width of the room is 12.5 feet. He knows that the formula for area is $\begin{aligned} A = l w \end{aligned}$ . He writes the following problem.
::Kevin需要找出一个房间的面积。这通常是一个简单的工程, 但尺寸小数为小数。房间的长度为9.5英尺。房间宽度为12.5英尺。他知道面积的公式是 A = l w。他写了下面的问题。

$\begin{aligned} A = (9.5 f t) (12.5 f t) \end{aligned}$

Now he is stuck. What should Kevin do?
::现在他卡住了 Kevin该怎么办?

In this concept, you will learn how to multiply decimals using area models.
::在此概念中,您将学习如何使用区域模型乘以小数。

Area Models
::地区模型

An area model is used to show a representation of multiplication or division. A rectangle is divided into columns and rows to represent the numbers. The product of two numbers is similar to finding the area of a rectangle.
::区域模型用于显示乘法或除法的表示。矩形分为列和行以代表数字。两个数字的产物与查找矩形区域相似。

$\begin{aligned} Area of a rectangle = length \times width \end{aligned}$

Here is a multiplication problem involving two decimal numbers.
::这是一个乘法问题,涉及小数点后两个数字。

$\begin{aligned} 0.3 \times 0.4 \end{aligned}$

Let’s start by thinking of a decimal using a hundreds grid to represent the hundredths of a decimal.
::让我们首先考虑小数点, 使用数百个网格代表小数点的百分百。

$\begin{aligned} 0.3 = 0.30 or 30 hundredths 0.4 = 0.40 or 40 hundredths \end{aligned}$

Shade 30 squares green vertically because 30 hundredths is also 30 out of 100.Shade 40 squares yellow horizontally because 40 hundredths is also 40 out of 100. Combine the two numbers on the same hundreds grid to see what it would look like to multiply these two decimals together.
::垂直形成30平方的绿色因为在100平方中,300平方是30 平方是100平方是40平方是10平方是10平方是10平方是40平方是100平方是40平方是100平方是40平方是40平方是10平方, 将同一数百方格上的这两个数字合并到一起看这两个小数的乘法是什么样子。

The shaded area created by the overlapping of the images is the product. The product of 0.3 times 0.4 is 12 hundredths or 0.12. Note than when you multiply a number by a decimal number less than one, the product will always be smaller than the number being multiplied.
::图像重叠所创造的阴影区域是产品。0.3乘以0.4的产物是1200倍或0.12。请注意,当您乘以数字乘以小数乘以小数乘以小数小于1时,产品总是小于乘以的数字。

Let’s look at another multiplication problem using the hundreds grid.
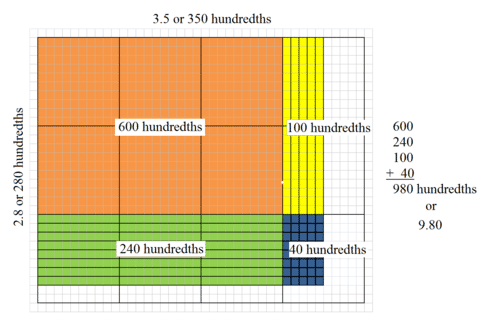
::让我们用数百个网格来研究另一个乘法问题。

$\begin{aligned} 2.8 \times 3.5 \end{aligned}$

Represent 2.8 as 280 hundredths vertically and 3.5 as 350 hundredths horizontally on the same area model.
::在同一区域模型上,垂直为2.8度为280度,水平为3.5度为350度。

Then, fill in the area to complete the rectangle.
::然后填满区域以完成矩形

Next, add up the number of units from each section.
::下一步,加起来每一节的单位数目。

The product of 2.8 times 3.5 is 9.80 or 9.8.
::2.8乘3.5的产物为9.80或9.8。

Using hundred grids might be enough for simple decimal numbers, but it can get complicated when it comes to large decimal numbers. For more complex numbers, you can convert the decimal numbers to whole numbers and then find the product using whole number area model multiplication.
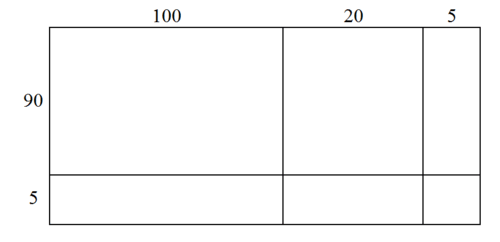
::使用百网格可能足够简单小数数字,但当涉及大小数数字时会变得复杂。对于更复杂的数字,您可以将小数数字转换为整数,然后用整个数字区域模型乘法找到产品。

Let’s use the same problem of $\begin{aligned} 2.8 \times 3.5 \end{aligned}$ . Notice that the area model above creates a rectangle that is 28 units wide and 35 units long. First, draw a rectangle to illustrate the area model with the same measurements. Break up the lengths and widths according to place values. The length is $\begin{aligned} 30 + 5 \end{aligned}$ units long. The width is $\begin{aligned} 20 + 8 \end{aligned}$ units wide. Note that the rectangle does not need to be drawn to scale.
::让我们使用2.8×3.5的相同问题。请注意, 以上区域模型创建的矩形宽28个单位, 长35个单位。首先, 绘制一个矩形来用相同的测量来说明区域模型。按位置值分隔长度和宽度。长度为 30 + 5 个单位。宽度为 20 + 8 个单位。请注意, 矩形不需要被拉动为缩放。

Then, multiply to find the areas of the smaller rectangles. The sum of the smaller areas should equal the area of the whole rectangle.
::然后,乘以找到较小矩形的区域。较小区域的总和应该等于整个矩形的区域。

Next, add the decimal point back into the area. Remember that the original problem was $\begin{aligned} 2.8 \times 3.5 \end{aligned}$ . Count the number of decimal places in the original problem. 2.8 has one decimal place and 3.5 also has one decimal place. There are a total of two decimal places. Take the sum and move the decimal point two places to the left.
::下一步, 将小数点再添加到区域中。记住, 最初的问题为2.8 × 3. 5。计算原始问题中的小数位数。 2. 8 小数点有一个小数点位数, 3. 5 小数点数也有一个小数点位数。总计是两个小数点数。请将总和移到左边的小数点 2 位数。

$\begin{aligned} 980 \to 9. \underset{\leftarrow}{8} \underset{\leftarrow}{0} \end{aligned}$

The area of the whole rectangle is 9.8 square units. Both area models produce the same result.
::整个矩形区域为9.8平方单位,两种区域模型的结果相同。

$\begin{aligned} 2.8 \times 3.5 = 9.80 \end{aligned}$

Examples
::实例

Example 1
::例1

Earlier, you were given a problem about Kevin’s area problem.
::Kevin的地盘问题。

Kevin has the formula for the area, but needs help multiplying the decimals.
::Kevin拥有这个区域的公式,但需要帮助将小数乘以小数。

$\begin{aligned} A = (12.5 f t) (9.5 f t) \end{aligned}$

First, use an area model representation. Change 12.5 and 9.5 to whole numbers and break up the numbers according to place value .
::首先,使用区域模型表示法。将12.5和9.5改为整数,并根据地点值将数字分开。

$\begin{aligned} \begin{array}{rcl} 12.5 \to 125 \to 100 + 20 + 5 \\ 9.5 \to 95 \to 95 + 5 \end{array} \end{aligned}$

Next, find the areas of the smaller rectangles.
::接下来,找到较小的矩形区域。

Add up the areas.
::添加区域。

$\begin{aligned} 9, 000 + 1, 800 + 450 + 500 + 100 + 25 = 11875 \end{aligned}$

Finally, place the decimal point into the sum. Count the number of decimal places in 12.5 and 9.5. There are a total of 2 decimal places. Move the decimal point 2 places to the left.
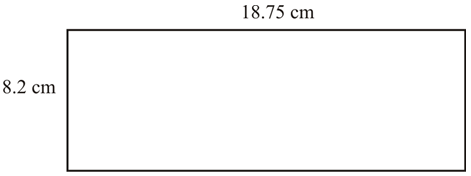
::最后,将小数点放在总和中。在12.5和9.5中计算小数位数。总小数点为2位数。将小数点2位数移到左边。

$\begin{aligned} 118. \underset{\leftarrow}{75} \end{aligned}$

$\begin{aligned} A = 118.75 f t^{2} \end{aligned}$

The area of the room is 118.75 square feet.
::房间面积为118.75平方英尺。

Example 2
::例2

Find the area using an area model.
::使用区域模型查找区域。

Aaron is going to stain his back deck. The deck measures 12.9 feet by 8.4 feet. Aaron needs the area of the deck in order to know how much wood stain he needs. How can he do this? What is the area of the deck?
::甲板的面积是12.9英尺乘8.4英尺。 Aaron需要甲板的面积才能知道他需要多少木质污点。他怎么能这样做呢?甲板的面积是多少?

To figure out the area of the deck, Aaron can use the formula for the area of a rectangle.
::亚伦可以使用矩形区域的公式来找出甲板的面积

$\begin{aligned} A = l w \end{aligned}$

First, substitute the given dimensions into the formula for length and width.
::首先,将给定尺寸替换为长度和宽度公式。

$\begin{aligned} A = (12.9 f t) (8.4 f t) \end{aligned}$

Then, use an area model representation. Change 12.9 and 8.4 to whole numbers and break up the numbers according to place value.Find the areas of the smaller rectangles.
::然后,使用区域模型表示。将12.9和8.4修改为整数,并根据地点值将数字分开。查找小矩形的区域。

$\begin{aligned} \begin{array}{rcl} 12.9 \to 129 \to 100 + 20 + 9 \\ 8.4 \to 84 \to 80 + 4 \end{array} \end{aligned}$

Next, add up the sum of the areas within the area model.
::接下来,加起来区域模型内的区域总和。

$\begin{aligned} 8, 000 + 1, 600 + 720 + 400 + 80 + 36 = 10, 836 \end{aligned}$

Finally, place the decimal point into the sum. Count the number of decimal places in 12.9 and 8.4. There are a total of 2 decimal places. Move the decimal point 2 places to the left.
::最后,将小数点放在总和中。在12.9和8.4中计算小数位数。总小数点为2位数。将小数点2位数移到左边。

$\begin{aligned} 108. \underset{\leftarrow}{36} \end{aligned}$

$\begin{aligned} A = 108.36 f t^{2} \end{aligned}$

The area of Aaron’s deck is 108.36 square feet.
::亚伦甲板面积为108.36平方英尺。

Example 3
::例3

Find the product using an area model.
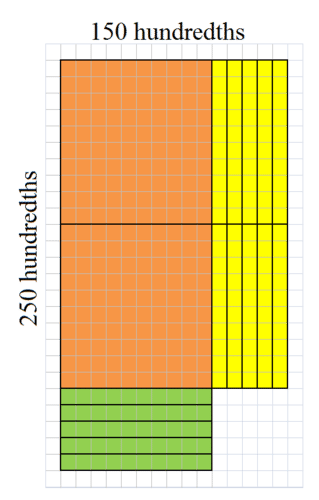
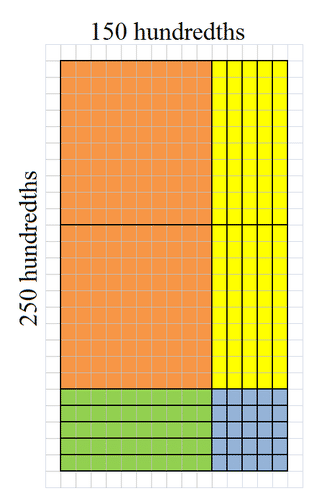
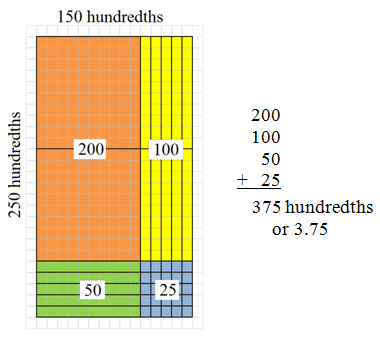
::使用区域模型寻找产品。

$\begin{aligned} 1.5 \times 2.5 \end{aligned}$

First, represent 1.5 horizontally and 2.5 vertically on the same area model. Change 1.5 and 2.5 to quantities of hundredths.
::首先,在同一个区域模型上横向为1.5,垂直为2.5。将1.5和2.5改为100倍。

$\begin{aligned} \begin{array}{rcl} 1.5 & = & 150 hundredths \\ 2.5 & = & 250 hundredths \end{array} \end{aligned}$

Then, fill in the area to complete the rectangle.
::然后填满区域以完成矩形

Then, add up the number of units in each section.
::然后将每一节的单位数目加起来。

The product of 1.5 times 2.5 is 3.75.
::1.5乘2.5的产物为3.75。

Example 4
::例4

Find the area using an area model.
::使用区域模型查找区域。

First, substitute the given dimensions into the formula for length and width.
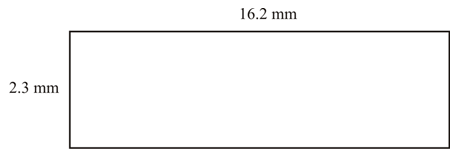
::首先,将给定尺寸替换为长度和宽度公式。

$\begin{aligned} A = (16.2 m m) (2.3 m m) \end{aligned}$

Then, use an area model representation. Change 16.2 and 2.3 to whole numbers and break up the numbers according to place value.
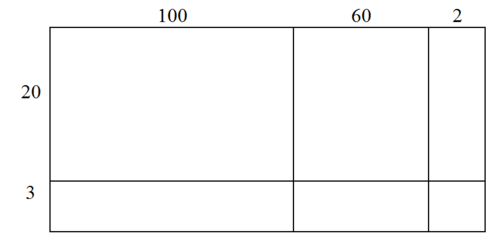
::然后,使用一个区域模型表示。将16.2和2.3修改为整数,并根据地点值将数字分开。

$\begin{aligned} \begin{array}{rcl} 16.2 \to 162 \to 100 + 60 + 2 \\ 2.3 \to 23 \to 20 + 3 \end{array} \end{aligned}$

Next, find the areas of the smaller rectangles.
::接下来,找到较小的矩形区域。

Add up the areas.
::添加区域。

$\begin{aligned} 2, 000 + 1, 200 + 300 + 180 + 40 + 6 = 3726 \end{aligned}$

Finally, place the decimal point into the sum. Count the number of decimal places in 16.2 and 2.3. There are a total of 2 decimal places. Move the decimal point 2 places to the left.
::最后,将小数点放在总和中。在16.2和2.3中计算小数位数。总小数点为2。将小数点 2 位移到左边。

$\begin{aligned} 37. \underset{\leftarrow}{26} \end{aligned}$

$\begin{aligned} A = 37.26 m m^{2} \end{aligned}$

The area is 37.26 square millimeters.
::面积37.26平方米。

Example 5
::例5

Find the product using an area model.
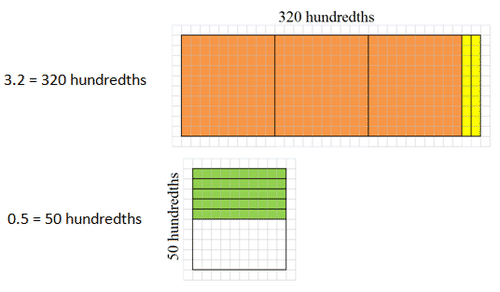
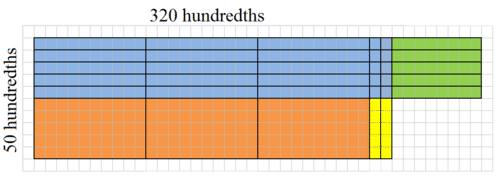
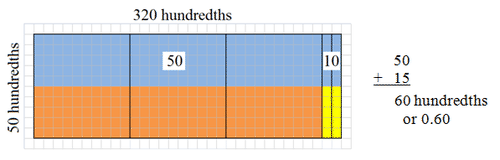
::使用区域模型寻找产品。

$\begin{aligned} 3.2 \times 0.5 \end{aligned}$

First, represent 3.2 horizontally and 0.5 vertically on the same area model. Change 3.2 and 0.5 to quantities of hundredths.
::首先,在同一个区域模型上水平代表3.2, 垂直表示0.5。将3.2 和 0.5 改为百分百。

Then, add up the number of units in the overlapping sections.
::然后在重叠的章节中加上单位数量。

The product of 3.2 times 0.5 is 0.6.
::3.2乘以0.5的产物为0.6。

Review
::回顾

Find the area of the following rectangles. You may round to the nearest hundredth.
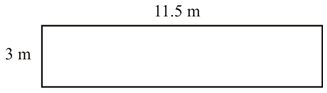
::查找以下矩形的区域。您可以绕到最近的一百个区域。

1.

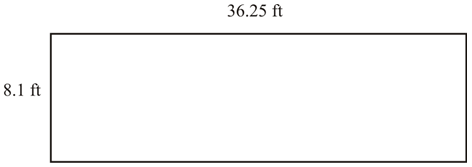
2.

3.

4.

5 .

6. $\begin{aligned} 12.5 f t \times 11.9 f t \end{aligned}$
::6.12.5 f t × 11.9 f t

7. $\begin{aligned} 6.5 i n \times 3.5 i n \end{aligned}$
::7.6.5 i n × 3.5 i n

8. $\begin{aligned} 12.3 m \times 9.5 m \end{aligned}$
::8. 12.3米×9.5米

9. $\begin{aligned} 16.2 m m \times 12.5 m m \end{aligned}$
::9. 16.2米m×12.5米

10. $\begin{aligned} 85.25 f t \times 29.5 f t \end{aligned}$
::10.85.25 f t × 29.5 f t

11. $\begin{aligned} 102.75 m \times 85.5 m \end{aligned}$
::102.75米×85.5米

12. $\begin{aligned} 109.5 m \times 100.2 m \end{aligned}$
::12.9.5米×100.2米

13. $\begin{aligned} 75.25 m \times 65.75 m \end{aligned}$
::13.75.25米×65.75米

14. $\begin{aligned} 189.5 m \times 120.75 m \end{aligned}$
::14.189.5米×120.75米

15. $\begin{aligned} 203.25 f t \times 150.75 f t \end{aligned}$
::15.203.25 f t × 150.75 f t

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

Resources
::资源

Section outline

Area Models ::地区模型

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

Example 5 ::例5

Review ::回顾

Review (Answers) ::回顾(答复)

Resources ::资源

Area Models
::地区模型

Examples
::实例

Example 1
::例1

Example 2
::例2

Example 3
::例3

Example 4
::例4

Example 5
::例5

Review
::回顾

Review (Answers)
::回顾(答复)

Resources
::资源