动态变化

播放段落

This smiley face has a number of distinct features, but does it have rotational symmetry ?
::这种笑脸有一些不同的特征, 但是否具有旋转对称性?

播放段落

In this concept, you will learn to recognize rotation transformations and rotational symmetry.
::在这个概念中,你将学会认识旋转转换和旋转对称。

播放段落

Rotation
::轮调

播放段落

A transformation is the movement of a geometric figure on the coordinate plane . A rotation is a type of transformation which is a turn. A figure can be turned clockwise or counterclockwise on the coordinate plane. In both transformations the size and shape of the figure stays exactly the same.
::转换是坐标平面上几何图的移动。 旋转是一种旋转的转换类型。 数字可以在坐标平面上按时针或逆时针旋转。 在两个转换中, 数字的大小和形状都保持完全相同 。

播放段落

A rotation is a transformation that turns the figure in either a clockwise or counterclockwise direction. You can turn a figure 90°, a quarter turn, either clockwise or counterclockwise. When you spin the figure exactly halfway, you have rotated it 180°. Turning it all the way around rotates the figure 360°.
::旋转是一个转换,将数字转换成时钟或反时钟方向。您可以将数字转换为90°,四分之一转,或者按时钟或反时钟。当将数字旋转到正中点时,您已经将数字旋转到180°。将数字旋转到整个方向,将数字旋转到360°。

播放段落

Look at the triangles below. The pink triangle is a 90° clockwise rotation or is a quarter turn.
::看看下面的三角形。粉红色三角形是90°的时钟旋转或四分之一的旋转。

播放段落

You could also turn the blue triangle 180°, which would turn the pink triangle completely upside down.
::你也可以翻转蓝色三角形180度, 粉红色三角形就会完全颠倒。

播放段落

Next, let’s look at an example of rotating figures on the coordinate plane.
::接下来,让我们看看协调飞机上旋转数字的例子。

播放段落

Rotate this figure 90° clockwise on the coordinate plane.
::在坐标平面上旋转此图 90 o 时钟 。

播放段落

First, write down the coordinates for each of the points of this pentagon .
::首先,写下这个五角形的每一个点的坐标。

播放段落

$\begin{align*}A (-3, 5)\end{align*}$
::A-3-5) (A-35)

播放段落

$\begin{align*}B (-4, 4)\end{align*}$
::B(4,4,4)项

播放段落

$\begin{align*}C (-3, 3)\end{align*}$
::C(-3,3)

播放段落

$\begin{align*}D(-1,2)\end{align*}$
:D-1,2)

播放段落

$\begin{align*}E (-1, 4)\end{align*}$

Next, the easiest way to think about rotating any figure is to think about it moving around a fixed point . In the case of graphing figures on the coordinate plane, you will be rotating the figures around the center point or origin .
::接下来,考虑任何数字旋转的最简单方式就是考虑它围绕固定点移动。如果在坐标平面上绘制图表,您将围绕中点或原点旋转数字。

播放段落

If you rotate a figure clockwise 90°, then you are going to be shifting the whole figure along the $\begin{align*}x\end{align*}$ -axis.
::如果您旋转一个数字时时速 90 度, 那么您将沿着 X 轴移动整个数字 。

播放段落

To figure out the coordinates of the new rotated figure, you switch the coordinates and then, you need to multiply the second coordinate by -1. This will make perfect sense given that the entire figure is going to shift.
::要找出新的旋转图的坐标, 您要切换坐标, 然后, 您需要将第二个坐标乘以 - 1 。 这将非常合理, 因为整个图将移动 。

播放段落

$$\begin{align*}\begin{array}{rcl} && \text{Original Points} \qquad \text{Coordinates Switched} \qquad y \text{-coordinate multiplied by} -1\\ && \qquad A (-3, 5) \qquad \qquad \quad \quad A^t (5, -3) \qquad \qquad \qquad \qquad \quad A^t(5, 3) \\ && \qquad B (-4, 4) \qquad \qquad \quad \quad B^t (4, -4) \qquad \qquad \qquad \qquad \quad B^t(4, 4) \\ && \qquad C (-3, 3) \qquad \qquad \quad \quad C^t (3, -3) \qquad \qquad \qquad \qquad \quad C^t(3, 3) \\ && \qquad D (-1, 2) \qquad \qquad \quad \quad D^t (2, -1) \qquad \qquad \qquad \qquad \quad D^t(2, 1) \\ && \qquad E (-1, 4) \qquad \qquad \quad \quad E^t (4, -1) \qquad \qquad \qquad \qquad \quad E^t(4, 1) \end{array}\end{align*}$$
::原始点坐标切换坐标乘以-1A(-3-5)At(5)-3)At(5)At(5)B(-4,4)Bt(4)Bt(4,4)Bt(4)C(3,3)Ct(3,3)Ct(3,3)D(-1,2)Dt(2,1)Dt(2,1)Dt(2,1)E(1,4)Et(4)-1)Et(4,1)Et(4,1)1)Ct(4)C(3,3)Ct(3)Ct(3,3)Ct(3,3)D(-1,2)Dt(2,1)Dt(2,1)Dt(2,1)E(1)E(1,4)Et(4)Et(4)-1)Et(4,1)Et(4,1)Ct(4,1)C(4)C(4,1)C(4,1)

播放段落

Then, graph this rotated figure. Notice that you use $\begin{align*}A^t\end{align*}$  to represent the rotated figure.
::然后, 请绘制此旋转图。 注意您使用 At 来表示旋转图 。

播放段落

Let’s think about what would happen to the figure if you were to rotate it counterclockwise. To do this, the figure would move across the $\begin{align*}y\end{align*}$ -axis in fact, the $\begin{align*}x\end{align*}$ -coordinates would change completely. In actuality, you would switch the original coordinates around. The $\begin{align*}x\end{align*}$ -coordinate would become the $\begin{align*}y\end{align*}$ -coordinate and the $\begin{align*}y\end{align*}$ -coordinate would become the $\begin{align*}x\end{align*}$ -coordinate. Then, you need to multiply the new $\begin{align*}x\end{align*}$ -coordinate by -1.
::让我们想一想如果你逆时针旋转这个数字会怎么样。要做到这一点,这个数字会横跨y轴,事实上,x坐标将完全改变。实际上,你将切换原来的坐标。x坐标将变成Y坐标,Y坐标将变成X坐标。然后,你需要将新的x坐标乘以-1。

播放段落

Let’s take a look.
::让我们来看看。

播放段落

$$\begin{align*}\begin{array}{rcl} && \text{Original Points} \qquad \text{Coordinates Switched} \qquad x \text{-coordinate multiplied by} -1\\ && \qquad A (-3, 5) \qquad \qquad \quad \quad A^t (5, -3) \qquad \qquad \qquad \qquad A^t(-5, -3) \\ && \qquad B (-4, 4) \qquad \qquad \quad \quad B^t (4, -4) \qquad \qquad \qquad \qquad B^t(-4, -4) \\ && \qquad C (-3, 3) \qquad \qquad \quad \quad C^t (3, -3) \qquad \qquad \qquad \qquad C^t(-3, -3) \\ && \qquad D (-1, 2) \qquad \qquad \quad \quad D^t (2, -1) \qquad \qquad \qquad \qquad D^t(-2, -1) \\ && \qquad E (-1, 4) \qquad \qquad \quad \quad E^t (4, -1) \qquad \qquad \qquad \qquad E^t(-4, -1) \end{array}\end{align*}$$
::原点坐标切换x坐标乘以-1A(3-5)At(5)At(5)-3)At(5)At(5)Bt(5)B(3)Bt(4)Bt(4)Bt(4)Bt(4)Bt(4)C(3)C(3)Ct(3)-4(3)Ct(3)-(3)Ct(3)-(3)D(2)Dt(2)-(1)Dt(2)Dt(2)-(1)E(4)Et(4)-1)Et(4)Et(4)-(4)-1)

播放段落

Let’s graph this new counterclockwise rotation.
::让我们绘制新的逆时针旋转图。

播放段落

You can also graph figures that have been rotated 180°. To do this, you multiply both coordinates of the original figure by -1.
::您也可以绘制旋转180°的图表。要做到这一点,将原始图的两个坐标乘以-1。

播放段落

Let’s see what this looks like.
::让我们看看这看起来像什么。

播放段落

$$\begin{align*}\begin{array}{rcl} && \text{Original Points} \qquad \qquad \ \text{Coordinates multiplied by} -1\\ && \qquad A (-3, 5) \qquad \qquad \quad \quad A^t (3, -5) \\ && \qquad B (-4, 4) \qquad \qquad \quad \quad B^t (4, -4) \\ && \qquad C (-3, 3) \qquad \qquad \quad \quad C^t (3, -3) \\ && \qquad D (-1, 2) \qquad \qquad \quad \quad D^t (1, -2) \\ && \qquad E (-1, 4) \qquad \qquad \quad \quad E^t (1, -4) \end{array}\end{align*}$$
::原始点乘以-1A(-3-5)At(3)B(-4,4)Bt(4)C(-4)C(-3,3)Ct(3)-3)D(-1,2)Dt(1)Dt(1,2)E(1,4)E(1,4)Et(1)-4)

播放段落

Let’s graph this 180° rotated image.
::让我们绘制180°旋转图像的图形。

播放段落

A figure has rotational symmetry if, when you rotate it, the figure appears to stay the same. The outlines do not change even as the figure turns.
::数字具有旋转对称性, 如果在旋转时, 数字似乎保持不变。 轮廓即使在图转动时也不会改变 。

播放段落

Let’s look at an example.
::让我们举个例子。

播放段落

The star will look the same even if you rotate it. You could turn it 72° or 144°   clockwise or counterclockwise, it won’t matter. The star will still appear the same.
::恒星即使旋转也会看起来一样。 您可以将恒星旋转72°或144°时钟或反时针, 也不会有关系。 恒星仍然会出现相同 。

播放段落

Examples
::实例

播放段落

Example 1
::例1

播放段落

Earlier, you were given a problem about  the smiley face. How can you determine if it has rotational symmetry?
::早些时候,有人给了你一个微笑表情的问题。你如何确定它是否具有旋转对称性?

播放段落

First, look at the outline of the image. The outline is a circle . A circle is the one shape that can be rotated less than 360° and still appears exactly the same. The circle is infinitely symmetrical because it keeps the shape no matter how many degrees it is moved or rotated.
::首先,看看图像的大纲。 大纲是一个圆。 圆是一个可以旋转小于360°, 并且仍然完全相同的形状。 圆是无限对称的, 因为它保持了形状, 不论它移动或旋转多少度 。

播放段落

Next, look at the design inside the image. If you rotate the circle, then the design inside will change.
::下一位, 看看图像中的设计。 如果您旋转圆, 那么里面的设计将会改变 。

播放段落

The answer is that the image does not have rotational symmetry.
::答案是图像没有旋转对称 。

播放段落

Example 2
::例2

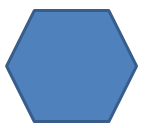
播放段落

Does a regular hexagon have rotational symmetry?
::正常的六边形有旋转对称吗?

播放段落

Look at the image of the regular hexagon below.
::看看下面的普通六边形图像。

播放段落

It has rotational symmetry. You can see that because you can rotate it 90° and 180° and it will still look exactly the same. You could rotate it less than 90° too and it still has rotational symmetry. You can also look at the angles to determine rotational symmetry. Each time we turn the figure, it has two parallel sides on the top and bottom and four other sides at the same angles. It has rotational symmetry.
::它具有旋转对称性。 您可以看到, 因为您可以旋转它 90 °和 180 °, 而且它看起来还是完全一样。 您也可以旋转它小于 90 °, 而且它仍然具有旋转对称性。 您也可以查看角度来确定旋转对称性。 每次我们翻转图时, 它的顶部和底部有两面平行, 同一角度有四面平行。 它具有旋转对称性 。

播放段落

Example 3
::例3

播放段落

Does a square have rotational symmetry?
::广场有旋转对称吗?

播放段落

Look at the image of the square below.
::看看下面方形的图象。

播放段落

Yes, the square has rotational symmetry because you can turn it and it will appear exactly the same.
::是的,广场是旋转对称的,因为你可以转动它, 它会看起来完全一样。

播放段落

Example 4
::例4

播放段落

Does the letter U have rotational symmetry?
::字母U有旋转对称吗?

播放段落

Look at the image of the letter U below.
::看看下面字母U的图像。

播放段落

No, the letter U does not have rotational symmetry because it will not appear the same if it is turned 90° clockwise or counterclockwise, or turned 180°.
::否,字母U没有旋转对称,因为如果转90°时钟或逆时针,或转180°,字母U就会看起来不同。

播放段落

Example 5
::例5

播放段落

Does a regular octagon have a rotational symmetry?
::普通八边形有旋转对称吗?

播放段落

Look at the image of the regular octagon below.
::看看下面的正八角形图像。

播放段落

Yes, the regular octagon has rotational symmetry because you can turn it and it will appear exactly the same.
::是的,普通的八边形具有旋转对称性, 因为你可以转动它, 它会看起来完全一样。

播放段落

Review
::回顾

播放段落

Answer the following questions about rotations, translations and tessellations.
::回答以下关于轮值、翻译和熔融的问题。

播放段落

1. What is a translation?
::1. 什么是翻译?

播放段落

2. What is a rotation?
::2. 什么是轮换?

播放段落

3. True or false. A figure can be translated up or down only.
::3. 真实的或虚假的,数字只能翻译成上或下。

播放段落

4. True or false. A figure can be translated 180°.
::4. 真实或虚假,数字可以翻译为180°。

播放段落

5. True or false. A figure can be rotated 90° clockwise or counterclockwise.
::5. 真实的或假的,数字可以按90°的时速或逆时针旋转。

播放段落

6. True or false. A figure can’t be translated 180°.
::6. 数字不能翻译180°。

播放段落

7. Given the point (x, y) what will the coordinates of this point be after it is rotated $\begin{align*}{90}^{\circ}\end{align*}$  counterclockwise?
::7. 鉴于(x, y)点,在逆时速90旋转后,该点的坐标将是什么?

播放段落

8. Given the point (x, y) what will the coordinates of this point be after it is rotated $\begin{align*}{90}^{\circ}\end{align*}$  clockwise?
::8. 鉴于这个点(x, y),如果按时速90旋转,这个点的坐标将是什么?

播放段落

9. Given the point (x, y) what will the coordinates of this point be after it is rotated  $\begin{align*}{80}^{\circ}?\end{align*}$
::9. 鉴于(x, y)点,在旋转 80 ° 后,该点的坐标将是什么?

播放段落

Given the following vertex coordinates write the new coordinates for each rotation given the directions. (Note that rotations happen about the origin.)
::根据以下的顶点坐标, 写下每次旋转的新坐标, 并给定方向 。 (请注意, 原点会发生旋转 。 )

播放段落

A Triangle with the coordinates (-4, 4) (-4, 2) and (-1, 1).
::带坐标(-4、4、4、4、4、2和1-1)的三角形。

播放段落

10. Rotate the figure 90° clockwise.
::10. 按时速90°旋转图。

播放段落

11. Rotate the figure 90° counterclockwise.
::11. 逆时针90度旋转图。

播放段落

12. Rotate the figure 180°.
::12. 旋转图180°。

播放段落

A Triangle with the coordinates (1, 3) (5, 1) (5, 3).
::三角形,坐标(1, 3) (5, 1) (5, 3) 。

播放段落

13. Rotate the figure clockwise 90°.
::13. 按时针90度旋转数字。

播放段落

14. Rotate the figure counterclockwise 90°.
::14. 逆时针90度逆时针旋转数字。

播放段落

15. Rotate the figure 180°.
::15. 旋转图180°。

播放段落

Review (Answers)
::回顾(答复)

播放段落

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。

 

播放段落

Resources
::资源