确定并使用切切率
章节大纲
-
Lois, who is enjoying her lunch in the park, notices a group of students from the University Forestry class measuring the length of a shadow cast by a large spruce tree. The students are also measuring the angle made by the sun with the ground.
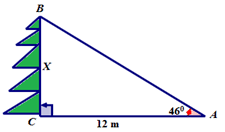
::露意丝正在公园享受午餐,他注意到一群大学林业班的学生测量了大树树的影子长度。 学生们也在用地面测量太阳的角。The shadow is 12 meters long and the angle of the sun is 46°. How can the students calculate the height of the tree without actually measuring it?
::阴影12米长,太阳角度46度,学生如何计算树高而不实际测量?In this concept, you will learn to determine and use the tangent ratio.
::在此概念中,您将学会确定并使用正切比例。Tangent Ratios
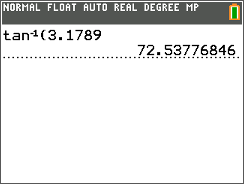
::相近比率You have used the TI-calculator to determine the measure of an angle using the inverse tangent function ( tan − 1 ) when the value of the ratio was known. If tan B = 3.1789 then using the TI-calculator displayed the measure of 72.5° for the angle.
::您已经使用 TI 计算器来确定角的度量, 在知道比值值时使用反正切函数( tan-1) 。 如果 TANB=3. 1789, 则使用 TI 计算器为角显示 72.5 ° 的度量 。The TI-calculator can also be used to find the ratio when the measure of the angle is known. If the measure of ∠ B = 37 ∘ then the value of the tangent ratio can be found by following the Key Press History:
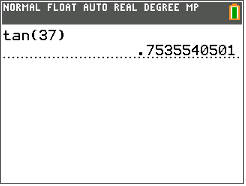
::也可以使用 TI- 计算器来在已知角度测量值时找到比值。 如果以 {B=37\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\可以按照 Key Press History 来找到正切比值 :On the calculator screen the following is displayed:
::在计算器屏幕上显示以下显示:This decimal should always be rounded to the nearest ten thousandth (four places after the decimal)
::此小数点应总是四舍五入到最接近的万分之一(小数点后四位)tan 37 ∘ = 0.7536
:c) 保护臭氧层;
This tangent ratio for an angle of 37° will remain constant regardless of the size of the triangle. The sides will always be in the same proportion to each other. The Tangent ratio can have very large or very small values depending on the triangle.
::角为37°的正切比将保持恒定, 不论三角形大小。 边将始终处于对齐比例。 Tangent 比例可以随三角形而有很大或很小的值 。The Tangent ratio is related to one of the acute angles of a right triangle such that the tangent of the acute angle is the ratio of the side adjacent to the specific acute angle (the reference angle) to the side opposite the acute angle. The Tangent ratio can be written as tan ∠ = opposite adjacent . This equation has three parts to it - an angle and two sides. When the lengths of the two sides are known, the measure of the angle can be calculated. When the measure of an angle and the length of one side is known, the length of the other side can be calculated.
::斜方比与右三角形的急性角之一有关,这样,急性角的正切值就是与特定急性角相邻的侧面(参考角)与对面的侧面之比。 斜方比可以写成 tanç oppositeadjatchacent 。 此方程有三个部分, 一个角度和两边。 当知道两边的长度时, 可以计算角的度量。 当知道角和一边的长度时, 可以计算另一侧的长度 。It is the sides of the triangle that determine the trigonometric ratio that will be used to calculate the measure of an angle or the length of a side. To use the tangent ratio, the adjacent and opposite sides of the right triangle, in relation to the reference angle , must be indicated. These two sides will have values on them if the measure of an angle is to be calculated using the tangent ratio. If the length of a side is to be calculated using the tangent ratio then one of the sides will display a value and the other will display a variable (the side that is unknown).
::三角形的侧面决定三角比, 用来计算角或边的长度。 要使用正切比, 则必须标明右三角形的相邻和对面与参考角的关系。 如果要用正切比来计算角的度量, 则这两边的侧面会有数值。 如果使用正切比来计算边的长度, 则其中一方将显示一个数值, 而另一方将显示一个变量( 未知的侧面 )。Let’s look at the following right triangle to see how this works.
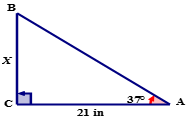
::让我们看看下面的右三角形,看看它是如何运作的。The measure of ∠ A is 37°. The length of side ¯ A C is 21 inches. The side ¯ B C has the variable ‘ X ’ on it which means this is the side that is unknown and its length must be calculated.
::QA的度量为37°。侧A的长度为 21 英寸。 侧BC 有变量 'X' , 这意味着这是未知的一面, 必须计算其长度 。The sides of the triangle can be named using the acute angle which is the reference angle for this triangle.
::三角形的两边可以使用急性角A命名,A是此三角形的参考角。The two sides that are indicated on this triangle are the opposite and the adjacent. The Tangent ratio is the ratio of the adjacent side to the opposite side.
::此三角形上显示的两边是对面和相邻的。 Tangent 比率是相邻侧与对面的比。First, write the tangent ratio using words.
::首先,用文字写下正切比。tan A = opposite adjacent
::tanA=对面近地点Next, write the tangent ratio using symbols.
::接下来,用符号写下正切比 。
::tanA = BCCNext, fill all known values into the equation. ∠ A = 37 ∘ ; ¯ A C = 21 ; ¯ B C = X .
::接下来,将所有已知的值填入方程。 @A=37;'AC=21;'BC=X。tan 37 ∘ = X 21
::tan37X21Next, use the TI-calculator to find the value of 37°. Round the decimal to the nearest ten thousandth.
::接下来,使用 TI 计算器查找值为 37 °。 将小数点舍入小数点到最接近的万分之一 。tan 37 ∘ = 0.7536
:c) 保护臭氧层;
Next, substitute this value into the equation.
::接下来,将这个值替换为等式 。tan 37 ∘ = X 21 0.7536 = X 21
::tan37X2.10.7536=X21Next, multiply both sides of the equation by 21 to solve for the variable.
::接下来,将方程的两边乘以 21 以解析变量 。0.7536 = X 21 21 ( 0.7536 ) = 21 ( X 21 ) 15.8256 = 1 21 ( X 21 ) 15.83 = X
::0.7536=X2121(0.7536)=21(X21)15.8256=121(X21)15.83=XThe answer is 15.83
::答案是15.83The length of the opposite side of the right triangle is 15.83 inches.
::右三角形对面的长度为15.83英寸。The calculated lengths of sides are usually expressed to the nearest hundredth while the calculated measure of an angle is usually expressed to the nearest tenth, unless otherwise stated.
::边的计算长度通常表示为最接近的一百,而角的计算尺度通常表示为最接近的十分之一,除非另有说明。Examples
::实例Example 1
::例1Earlier, you were given a problem about the students and the spruce tree. They need to calculate the height of the spruce tree without actually measuring it.
::早些时候,有人给了你一个关于学生和树苗的问题。他们需要计算树苗的高度,而无需实际测量。To do this, they can use the tangent ratio.
::要做到这一点,他们可以使用正切比例。First, draw and label a right triangle to model the problem.
::首先,绘制并标出一个右三角形来模拟问题。Next, name the sides of the triangle using the reference angle A .
::下一步,使用参考角度 A 命名三角形的边。Next, write the Tangent ratio using words.
::下一位,用文字写出同音比 。tan A = opposite adjacent
::tanA=对面近地点Next, write the Tangent ratio using symbols.
::接下来,用符号来写"唐根比"tan A = B C A C
::tanA = BCCNext, fill all known values into the equation. ∠ A = 46 ∘ ; ¯ A C = 12 ; ¯ B C = X .
::接下来,将所有已知的值填入方程 。 @A=46;'AC=12;'BC=X。tan 46 ∘ = X 12
::tan46X12Next, use the TI-calculator to find the value of tan 46 ∘ .
::接下来,使用 TI 计算器来查找 tan46 的值 。tan 46 ∘ = 1.0355
::tan461.0355Next, substitute this value into the equation.
::接下来,将这个值替换为等式 。tan 46 ∘ = X 12 1.0355 = X 12
::tan46*X121.0355=X12Next, multiply both sides of the equation by 12 to solve for the variable.
::接下来,将方程的两边乘以 12 来解答变量 。1.0355 = X 12 12 ( 1.0355 ) = 12 ( X 12 ) 12.426 = 1 12 ( X 12 ) 12.43 = X
::1.0355=X122(1.0355)=12(X1212)12.426=112(X12)12.43=XThe answer is 12.43.
::答案是12.43。The height of the tree is 12.43 meters.
::树高12.43米Example 2
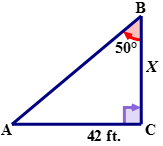
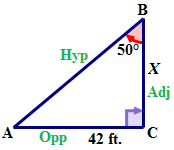
::例2For the following right triangle calculate the length of side ‘ X ’ to the nearest hundredth.
::以下的右三角形计算“X”到最接近的百分百的侧边长度。First, use the reference angle to name the sides of the triangle.
::首先,使用引用角度 B 来命名三角形的侧面。The two sides that are indicated on this triangle are the adjacent and the opposite. The Tangent ratio is the ratio of the adjacent side to the opposite side.
::三角形上标明的两边是相邻和对面。Tangent比率是相邻侧与对面之比。First, write the tangent ratio using words.
::首先,用文字写下正切比。tan B = opposite adjacent
::tanB = 对面近地点Next, write the tangent ratio using symbols.
::接下来,用符号写下正切比 。tan B = A C B C
::tanB = ACBCNext, fill all known values into the equation. ∠ B = 50 ∘ ; ¯ B C = X ; ¯ A C = 42 .
::接下来,将所有已知的值填入方程 。 @ @ B=50 @ ; ‘ BC=X; ’ AC=42 。tan B = A C B C tan 50 ∘ = 42 X
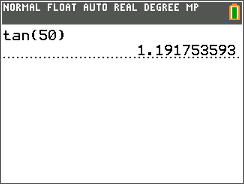
::tanB = ACBCtan50 42XNext, use the TI-calculator to find the value of tan 50 ∘ .
::接下来,使用 TI 计算器来查找 tan50 的值 。tan 50 ∘ = 1.1918
::1.1918年1月1日Next, substitute this value into the equation.
::接下来,将这个值替换为等式 。tan 50 ∘ = 42 X 1.1918 = 42 X
::tan5042X1.1918=42XNext, multiply both sides of the equation by X to clear the denominator.
::接下来,将方程的两侧乘以 X 来清除分母。1.1918 = 42 X X ( 1.1918 ) = X ( 42 X ) 1.1918 X = 1 X ( 42 X ) 1.1918 X = 42
::1,1918=42XX(1.1918)=X(42X)1,1918X=1X(42X)1,1918X=42Then, divide both sides of the equation by 1.1918 to solve for the variable.
::然后将方程的两边除以 1,1918 来解析变量 。1.1918 X = 42 1 1.1918 X 1.1918 = 42 1.1918 X = 35.24
::1.1918X=421118X119181818=4211918X=3524The answer is 35.24.
::答案是35.24The length of the adjacent side of the right tringle is of the right triangle is 35.24 feet.
::右三角形的右的相邻侧长度为35.24英尺。Example 3
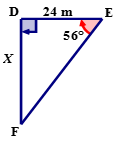
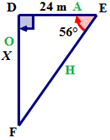
::例3For the following right triangle calculate the length of side ‘ X ’.
::以下右三角形计算侧边“X”的长度。First, use the reference angle E to name the sides of the triangle.
::首先,使用引用角度E来命名三角形的侧面。The two sides that are indicated on this triangle are the adjacent and the opposite. The Tangent ratio is the ratio of the adjacent side to the opposite side.
::三角形上标明的两边是相邻和对面。Tangent比率是相邻侧与对面之比。First, write the Tangent ratio using words.
::首先,用单词来写"唐根比"。tan E = opposite a d j a c e n t
::tanE=对面近地点Next, write the tangent ratio using symbols.
::接下来,用符号写下正切比 。tan E = D F D E
::tanE=DFDE 含二二二二二二二二二二二二二二二二二二二二二二二二二二二二二二二二二二二二二二二二二二二二二二二二二二二二二二二二二二二二二二二二二二二二二二二二二二二二二二二二二二二二二二二二二二二二二二二二二二二二二二二二二二二二二二二二二二二二二二二二二二二二二二二二Next, fill all known values into the equation. ∠ E = 56 ∘ ; ¯ D F = X ; ¯ D E = 24 .
::接下来,将所有已知的值填入方程 。 @ E=56 {; 'DF=X; DE=24 。tan E = D F D E tan 56 ∘ = X 24
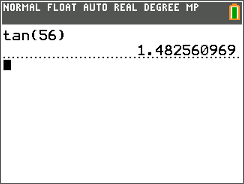
::tanE = DDDEtan56X24Next, use the TI-calculator to find the value of tan 56 ∘ .
::接下来,使用 TI 计算器来查找 tan56 的值 。tan 56 ∘ = 1.4826
::tan561.4826Next, substitute this value into the equation.
::接下来,将这个值替换为等式 。tan 56 ∘ = X 24 1.4826 = X 24
::tan56X241. 4826=X24Next, multiply both sides of the equation by 24 to solve for the variable.
::接下来,将方程的两边乘以 24 来解答变量 。1.4826 = X 24 24 ( 1.4826 ) = 24 ( X 24 ) 24 ( 1.4826 ) = 1 24 ( X 24 ) 35.58 = X
::1.4826=X2424(1.4826)=24(X2424)(1.4826)=124(X24)35.58=XThe answer is 35.58.
::答案是35.58The length of the opposite side of the right triangle is 35.58 meters.
::右三角形对面的长度为35.58米。Example 4
::例4Use the TI-calculator to determine the missing measure.
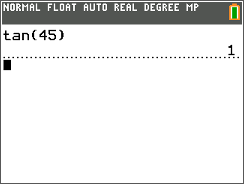
::使用 TI 计算器确定缺失的计量 。i) tan 45 ∘ = x 15
:一) tan45x15
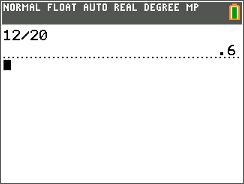
ii) tan B = 12 20
:二) tanB=1220
iii) If ∠ A = 82 ∘ then tan A = _
:三) 如果A=82a,则tanA=________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
tan 45 ∘ = x 15
::tan45x15i) First, use the TI-calculator to find the value of tan 45 ∘ .
:一) 首先,使用TI计算器来寻找 tan45 的值。
tan 45 ∘ = 1
::tan451Next, fill this value into the equation.
::接下来,把这个值填进方程中。tan 45 ∘ = x 15 1 = x 15
::tan45x151=x15Then, multiply both sides of the equation by 15 to solve for the variable.
::然后,将方程两侧乘以 15 来解答变量。1 = x 15 15 ( 1 ) = 15 ( x 15 ) 15 = 15 ( x 15 ) 15 = x
::1=x1515(1)=15(x1515)15=15(x1515)15=15(x1515)15=xThe answer is 15.
::答案是15岁ii) tan B = 12 20
:二) tanB=1220
First, use the TI-calculator to express the fraction as a decimal.
::首先,使用 TI 计算器将分数表示为十进制 。tan B = 12 20
::淡B=1220Next, rewrite the equation using the decimal form of the fraction.
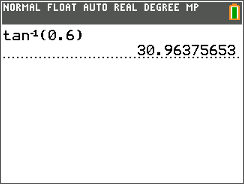
::下一步,使用分数的小数位数格式重写方程式。tan B = 0.6
::tanB=0.6 皮肤B=0.6Next, use the inverse tangent function ( tan − 1 ) to calculate the measure of ∠ B .
::下一步,使用反正切函数(tan-1)来计算 {B} 的度量。Then, round the answer to the nearest tenth.
::然后,将答案转至最近的十分之一。∠ B = 31.0 ∘
::B=31.0iii) if ∠ A = 82 ∘ then tan A = _
:三) 如果A=82a,那么tanA=______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
First, use the TI-calculator to determine the value of 82°.
::首先,使用TI计算器确定82°的数值。Then, round the answer to the nearest ten thousandth.
::然后把答案绕到最近的一万分之一tan 82 ∘ = 7.1154
::tan827.1154Review
::回顾Use a calculator to figure out each Tangent. You may round to the nearest hundredth.
::使用计算器来计算每个唐氏体。 您可以圆到最近的一百位 。1. Tangent 7°
::1. 近近7度2. Tangent 41°
::2. 近点41°3. Tangent 65°
::3. 延近65度4. Tangent 22°
::4. 延下22度5. Tangent 18°
::5. 中位18度6. Tangent 35°
::6. 近近35度7. Tangent 50°
::7. 近近50度8. Tangent 54°
::8. 近近54度9. Tangent 66°
::9. 延经66度10. Tangent 70°
::10. 倾角70度Find the length of the opposite side in each example. Round your answer to the nearest hundredths place.
::在每个示例中查找对面的长度。 将您的答案四舍五入到最近的百个位置 。11. We have a right triangle. Angle is 45 degrees. The side of the triangle adjacent to angle is 6 inches. What is the length of the opposite side?
::11. 我们有一个右三角形,角A为45度,角A附近三角形的侧面为6英寸,对面的长度是多少?12. We have a right triangle. Angle is 63 degrees. The side of the triangle adjacent to angle is 7 inches. What is the length of the opposite side?
::12. 我们有一个右三角形,角B为63度,角B附近三角形的侧面为7英寸,对角B的长度是多少?13. We have a right triangle. Angle is 29 degrees. The side of the triangle adjacent to angle is 6 inches. What is the length of the opposite side?
::13. 我们有一个右三角形,角A为29度,角A附近三角形的侧面为6英寸,对面的长度是多少?14. We have a right triangle. Angle is 12 degrees. The side of the triangle adjacent to angle is 4.5 inches. What is the length of the opposite side?
::14. 我们有一个右三角形,角B为12度,角B附近三角形的侧面为4.5英寸,对角B的长度是多少?15. We have a right triangle. Angle is 9 degrees. The side of the triangle adjacent to angle A is 8 inches. What is the length of the opposite side?
::15. 我们有一个右三角形,角A为9度,角A附近三角形的侧面为8英寸,反面的长度是多少?Review (Answers)
::回顾(答复)Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。