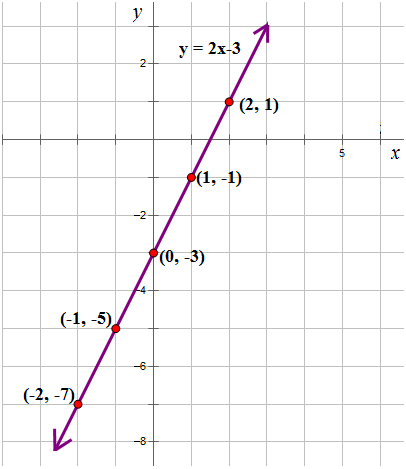Section: 图表函数 | 9.5 使用图表函数

Section outline

The students of the local high school are selling potted plants to raise funds for their soccer team to buy new uniforms. Each six-pack of potted plants will sell for $6.50. A new sports store has agreed to match the money raised by the students as a donation to the team. The money raised by the students will be displayed on a poster-size Cartesian graph and presented to the sports store. How can the students create such a graph?
::当地高中学生正在出售陶瓷工厂,为足球队募集资金购买新制服。每六包陶瓷工厂将出售6.50美元。一家新的体育商店同意将学生筹集的钱与团队捐款相匹配。学生筹集的钱将张贴在一张规模为卡提斯的海报图表上,并展示给体育商店。学生如何制作这样的图表?

In this concept, you will learn to use tables to graph functions.
::在此概念中,您将学会用表格来图形函数。

Graphing Functions
::图图函数

Consider the following Cartesian graph that represents the equation $\begin{align*}y=3x+4\end{align*}$ .
::考虑以下表示y=3x+4方程式的笛卡尔图。

The equation $\begin{align*}y=3x+4\end{align*}$ is written in function form and can be used to create a table of values that will make the statement of equality true. Remember an equation written in function form can be used to determine values for the output ‘ $\begin{align*}y\end{align*}$ ’ based on the different input ‘ $\begin{align*}x\end{align*}$ ’ values substituted into the equation.
::y= 3x+ 4 等式以函数形式写成, 可用于创建使平等声明真实化的数值表。记住以函数形式写成的公式可以用来根据方程式中替代的不同输入 ' x ' 值来确定输出 'y ' 的值。

Using $\begin{align*}x\end{align*}$ -values of -4, -2, 0, 2 and 4, create a table of values to represent the equation $\begin{align*}y=3x+4\end{align*}$ .
::使用 4 - 2, 0, 2 和 4 的 x 值, 创建一个数值表, 以代表 y= 3x+ 4 的方程式。

$\begin{align}x\end{align}$	$\begin{align}y\end{align}$
-4	-8
-2	-2
0	4
2	10
4	16

\begin{aligned} \begin{array}{rcl} x & = & - 4 \\ y & = & 3 x + 4 \\ y & = & 3 (- 4) + 4 Substitute x = - 4 into the equation . \\ y & = & - 12 + 4 Perform the multiplication to clear the parenthesis . \\ y & = & - 8 Simplify the right side of the equation . \end{array} \end{aligned}

$\begin{align*} \begin{array}{rcl} x&=&-4\\ y&=&3x+4\\ y&=&3(-4)+4 \qquad \text{Substitute } x=-4 \text{ into the equation}. \\ y&=&-12+4 \qquad \ \ \ \text{Perform the multiplication to clear the parenthesis}. \\ y&=&-8 \qquad \qquad \quad \text{Simplify the right side of the equation}. \end{array}\end{align*}$
::x4y=3x+4y=3(- 4)+4Subtitution x4 进入方程式。y12+4 执行乘法以清除括号 y8 简化方程式的右侧。

Use this process to calculate the values of the output variable for each of the given input values.
::使用此进程计算每个给定输入值输出变量的值。

\begin{aligned} \begin{array}{rcl} Given input value x & = & - 2 \\ y & = & 3 x + 4 \\ y & = & 3 (- 2) + 4 \\ y & = & - 6 + 4 \\ The output value is y & = & - 2 \end{array} \end{aligned}

$\begin{align*}\begin{array}{rcl} \text{Given input value }x&=&-2\\ y&=&3x+4\\ y&=&3(-2)+4\\ y&=&-6+4\\ \text{The output value is }y&=&-2 \end{array}\end{align*}$
::给定输入值 x% 2y= 3x+4y= 3(-2)+4y @ 6+4 输出值为 y2

\begin{aligned} \begin{array}{rcl} Given input value x & = & 0 \\ y & = & 3 x + 4 \\ y & = & 3 (0) + 4 \\ y & = & 0 + 4 \\ The output value is y & = & 4 \end{array} \end{aligned}

$\begin{align*}\begin{array}{rcl} \text{Given input value }x&=&0\\ y&=&3x+4\\ y&=&3(0)+4\\ y&=&0+4\\ \text{The output value is }y&=&4 \end{array}\end{align*}$
::给定输入值 x=0y=3x+4y=3( 0)+4y=0+4=4 输出值为y=4

\begin{aligned} \begin{array}{rcl} Given input value x & = & 2 \\ y & = & 3 x + 4 \\ y & = & 3 (2) + 4 \\ y & = & 6 + 4 \\ The output value is y & = & 10 \end{array} \end{aligned}

$\begin{align*}\begin{array}{rcl} \text{Given input value }x&=&2\\ y&=&3x+4\\ y&=&3(2)+4\\ y&=&6+4\\ \text{The output value is }y&=&10 \end{array}\end{align*}$
::给定输入值 x=2y=3x+4y=3(2)+4y=6+4 输出值为y=10

\begin{aligned} \begin{array}{rcl} Given input value x & = & 4 \\ y & = & 3 x + 4 \\ y & = & 3 (4) + 4 \\ y & = & 12 + 4 \\ The output value is y & = & 16 \end{array} \end{aligned}

$\begin{align*}\begin{array}{rcl} \text{Given input value }x&=&4\\ y&=&3x+4\\ y&=&3(4)+4\\ y&=&12+4\\ \text{The output value is }y&=&16 \end{array}\end{align*}$
::给定输入值 x=4y=3x+4y=3(4)+4y=12+4 输出值为y=16

The input value associated with the corresponding output value can be written as an ordered pair $\begin{align*}(x,y)\end{align*}$ such that $\begin{align*}(-4,-8), (-2,-2), (0,8), (2,10) \text{ and } (4,16)\end{align*}$ are the ordered pairs that can be plotted to represent the equation $\begin{align*}y=3x+4\end{align*}$ .
::与相应输出值相关的输入值可以写成一对定购对(x,y),这样(-4,8,(-2,-2),(2),(0),(8),(2),(2,10)和(4,16),即可以绘制成一对定购对以表示y=3x+4的公式。

The ordered pairs are plotted on the Cartesian graph and are shown as red points. These points were then joined by a smooth straight line to draw the graph. The graph is a straight line such that the equation that produced this line was a linear function . The highest exponent of the variables of a linear function is one.
::定单对配方在笛卡尔图上绘制,以红点显示。然后将这些点用一条平滑的直线连接以绘制图形。该图是一条直线线,因此产生这条线的方程式是一个线性函数。线性函数变量的最大引号是一条。

There are two special that produce a straight line graph. One of the straight lines is a vertical line that is parallel to the $\begin{align*}y\end{align*}$ -axis and the other is a horizontal line that is parallel to the $\begin{align*}x\end{align*}$ -axis.
::有两个特殊的直线图形。其中一条直线是一条与 Y 轴平行的垂直线,另一条是一条与 X 轴平行的水平线。

Let’s graph each of these special lines.
::让我们把这些特别的线条都图解一下。

A line having $\begin{align*}x=5\end{align*}$ as its equation will pass through the point $\begin{align*}(5,0)\end{align*}$ such that it will be parallel to the $\begin{align*}y\end{align*}$ -axis.
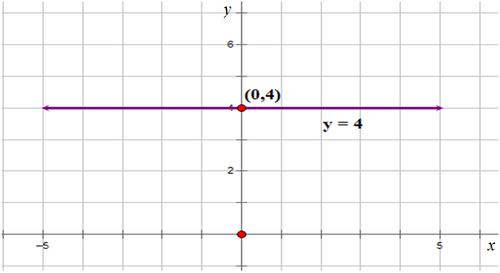
::直线x=5, 其方程将穿过点( 5,0) , 从而与 Y 轴平行。

A line having $\begin{align*}y=4\end{align*}$ as its equation will pass through the point $\begin{align*}(0,4)\end{align*}$ such that it will be parallel to the $\begin{align*}x\end{align*}$ -axis.
::以 y=4 为方程式的线将穿过点( 0, 4), 使其与 X 轴平行。

Examples
::实例

Example 1
::例1

Earlier, you were given a problem about the plotted plants and the soccer uniforms.
::早些时候,有人给了你一个问题有关布置的植物和足球制服。

The students need to create a poster size graph to show how much money was raised. How can the students create this graph?
::学生们需要创建海报大小图,以显示筹集了多少钱。学生们如何创建这个图?

They can create a table of values and plot the ordered pairs from the table.
::他们可以创建一个数值表,并从表中绘制一对定购的配对。

First, write an equation in function form to represent the sale of potted plants.
::首先,以功能形式写一个方程,表示出售陶工厂。

Let $\begin{align*}y\end{align*}$ represent the money raises and let $\begin{align*}x\end{align*}$ represent the number of potted plants sold.
::让x代表出售的陶工厂的数量。

\begin{aligned} y = 6.50 x \end{aligned}

$\begin{align*}y=6.50x\end{align*}$
::y=6. 50x

Next, create a table of values and use the equation expressed in function form to calculate the output value for each input value.
::下一步,创建一个数值表,并使用以函数格式表示的方程式计算每个输入值的输出值。

$\begin{align}x\end{align}$	$\begin{align}y\end{align}$
50
100
150
200
250

\begin{aligned} \begin{array}{rcl} x & = & 50 \\ y & = & 6.50 x \\ y & = & 6.50 (50) Substitute x = 50 into the equation . \\ y & = & $ 325.00 Perform the multiplication to clear the parenthesis . \end{array} \end{aligned}

$\begin{align*} \begin{array}{rcl} x&=&50\\ y&=&6.50x\\ y&=&6.50(50) \qquad \text{Substitute } x=50 \text{ into the equation}. \\ y&=&\$325.00 \qquad \ \text{Perform the multiplication to clear the parenthesis}. \end{array}\end{align*}$
::x=50y = 6. 50xy = 6. 50( 50) 等式中的替代 x= 50.y = 325. 00 进行乘法以清除括号。

Repeat the same process for the remaining input values.
::对剩余输入值重复相同的进程。

\begin{aligned} \begin{array}{rcl} Given input value x & = & 100 \\ y & = & 6.50 x \\ y & = & 6.50 (100) \\ The output value is y & = & $ 650.00 \end{array} \end{aligned}

$\begin{align*}\begin{array}{rcl} \text{Given input value }x&=&100\\ y&=&6.50x\\ y&=&6.50(100)\\ \text{The output value is }y&=&\$650.00 \end{array}\end{align*}$
::给定输入值 x= 100y= 6. 50xy= 6. 50( 100) 输出值为y= 650.00

\begin{aligned} \begin{array}{rcl} Given input value x & = & 150 \\ y & = & 6.50 x \\ y & = & 6.50 (150) \\ The output value is y & = & $ 975.00 \end{array} \end{aligned}

$\begin{align*}\begin{array}{rcl} \text{Given input value }x&=&150\\ y&=&6.50x\\ y&=&6.50(150)\\ \text{The output value is }y&=&\$975.00 \end{array}\end{align*}$
::给定输入值 x=150y=6. 50xy=6. 50(150) 输出值为y= 975. 00

\begin{aligned} \begin{array}{rcl} Given input value x & = & 200 \\ y & = & 6.50 x \\ y & = & 6.50 (200) \\ The output value is y & = & $ 1300.00 \end{array} \end{aligned}

$\begin{align*}\begin{array}{rcl} \text{Given input value }x&=&200\\ y&=&6.50x\\ y&=&6.50(200)\\ \text{The output value is }y&=&\$1300.00 \end{array}\end{align*}$
::给定输入值 x=200y=6. 50xy=6. 50(200) 输出值为y=1300.00

\begin{aligned} \begin{array}{rcl} Given input value x & = & 250 \\ y & = & 6.50 x \\ y & = & 6.50 (250) \\ The output value is y & = & $ 1625.00 \end{array} \end{aligned}

$\begin{align*}\begin{array}{rcl} \text{Given input value }x&=&250\\ y&=&6.50x\\ y&=&6.50(250)\\ \text{The output value is }y&=&\$1625.00 \end{array}\end{align*}$
::给定输入值 x= 250y= 6. 50xy= 6. 50(250) 输出值为 y= 1625. 00

Next, write the calculated ‘ $\begin{align*}y\end{align*}$ ’ values in the table.
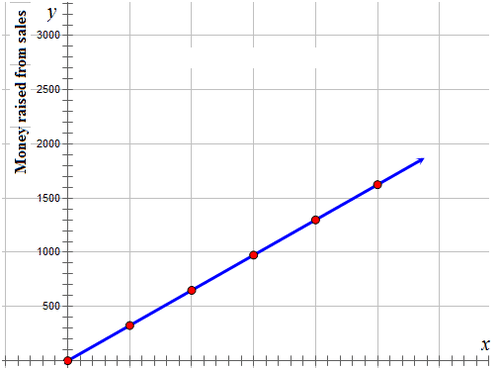
::下一步,在表格中填入计算中的 'y ' 值。

$\begin{align}x\end{align}$	$\begin{align}y\end{align}$
50	325
100	650
150	975
200	1300
250	1625

Then, plot the ordered pairs shown in the table on a Cartesian grid.
::然后,在笛卡尔网格上绘制桌子上显示的两对定购的配对。

The sports store will have to match the $1,625.00 raised by the students.
::体育商店将须与学生筹集的1 625.00美元相匹配。

Example 2
::例2

For the following linear function written in function form, complete the table of values and plot the graph.
::对于以函数形式写成的以下线性函数,填写数值表并绘制图表。

\begin{aligned} y = 3 x - 4 \end{aligned}

$\begin{align*}y=3x-4\end{align*}$
::y=3x- 4 y

$\begin{align}x\end{align}$	$\begin{align}y\end{align}$
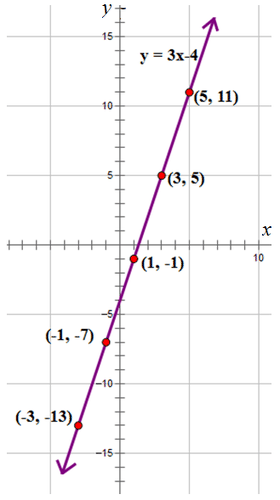
-3	-13
-1	-7
1	-1
3	5
5	11

First, use the equation to calculate the output values ‘ $\begin{align*}y\end{align*}$ .’
::首先,使用方程式计算输出值“y.”

\begin{aligned} \begin{array}{rcl} x & = & - 3 \\ y & = & 3 x - 4 \\ y & = & 3 (- 3) - 4 Substitute x = - 3 into the equation . \\ y & = & - 9 - 4 Perform the multiplication to clear the parenthesis . \\ y & = & - 13 Simplify the right side of the equation . \end{array} \end{aligned}

$\begin{align*} \begin{array}{rcl} x&=&-3\\ y&=&3x-4\\ y&=&3(-3)-4 \qquad \text{Substitute } x=-3 \text{ into the equation}. \\ y&=&-9-4 \qquad \quad \ \text{Perform the multiplication to clear the parenthesis}. \\ y&=&-13 \qquad \qquad \ \ \text{Simplify the right side of the equation}. \end{array}\end{align*}$
::x3y= 3x-4y= 3(-3)- 4Subtitution x3 进入方程式。 y9- 4 进行乘法以清除括号。 y13 简化方程式的右侧。

Repeat the process to calculate the values for the variable ‘ $\begin{align*}y\end{align*}$ .’
::重复计算变量“y.”的值的过程

\begin{aligned} \begin{array}{rcl} Given input value x & = & - 1 \\ y & = & 3 x - 4 \\ y & = & 3 (- 1) - 4 \\ y & = & - 3 - 4 \\ The output value is y & = & - 7 \end{array} \end{aligned}

$\begin{align*}\begin{array}{rcl} \text{Given input value }x&=&-1\\ y&=&3x-4\\ y&=&3(-1)-4\\ y&=&-3-4\\ \text{The output value is }y&=&-7 \end{array}\end{align*}$
::给定输入值 x% 1y= 3x- 4y= 3( - 1) - 4y_ 3- 4) 输出值为 y 7

\begin{aligned} \begin{array}{rcl} Given input value x & = & 1 \\ y & = & 3 x - 4 \\ y & = & 3 (1) - 4 \\ y & = & 3 - 4 \\ The output value is y & = & - 1 \end{array} \end{aligned}

$\begin{align*}\begin{array}{rcl} \text{Given input value }x&=&1\\ y&=&3x-4\\ y&=&3(1)-4\\ y&=&3-4\\ \text{The output value is }y&=&-1 \end{array}\end{align*}$
::给定输入值 x=1y=3x- 4y=3(1)- 4y=3- 4y=3- 4 输出值为 y1

\begin{aligned} \begin{array}{rcl} Given input value x & = & 3 \\ y & = & 3 x - 4 \\ y & = & 3 (3) - 4 \\ y & = & 9 - 4 \\ The output value is y & = & 5 \end{array} \end{aligned}

$\begin{align*}\begin{array}{rcl} \text{Given input value }x&=&3\\ y&=&3x-4\\ y&=&3(3)-4\\ y&=&9-4\\ \text{The output value is }y&=&5 \end{array}\end{align*}$
::给定输入值 x= 3y= 3x- 4y= 3(3)--4y= 9- 4y= 9- 4 输出值为 y= 5

\begin{aligned} \begin{array}{rcl} Given input value x & = & 5 \\ y & = & 3 x - 4 \\ y & = & 3 (5) - 4 \\ y & = & 15 - 4 \\ The output value is y & = & 11 \end{array} \end{aligned}

$\begin{align*}\begin{array}{rcl} \text{Given input value }x&=&5\\ y&=&3x-4\\ y&=&3(5)-4\\ y&=&15-4\\ \text{The output value is }y&=&11 \end{array}\end{align*}$
::给定输入值 x= 5y= 3x- 4y= 3(5)- - 4y= 15- 4 输出值为 Y= 11

Write the calculated ‘ $\begin{align*}y\end{align*}$ ’ values in the table.
::在表格中写入计算中的 'y ' 值。

Plot the ordered pairs on the Cartesian grid and join the plotted points with a smooth, straight line.
::在笛卡尔网格上标定的一对配对,用平滑的直线加入绘图点。

Example 3
::例3

For the following linear function create a table of values and plot the points to draw the graph:
::对于以下线性函数,将创建一个数值表,并绘制绘制图形的点数:

\begin{aligned} y = 2 x - 3 \end{aligned}

$\begin{align*}y=2x-3\end{align*}$
::y=2x-3

First, use the equation to calculate the output values ‘ $\begin{align*}y\end{align*}$ .’
::首先,使用方程式计算输出值“y.”

\begin{aligned} \begin{array}{rcl} x & = & - 2 \\ y & = & 2 x - 3 \\ y & = & 2 (- 2) - 3 Substitute x = - 2 into the equation . \\ y & = & - 4 - 3 Perform the multiplication to clear the parenthesis . \\ y & = & - 7 Simplify the right side of the equation . \end{array} \end{aligned}

$\begin{align*} \begin{array}{rcl} x&=&-2\\ y&=&2x-3\\ y&=&2(-2)-3 \qquad \text{Substitute } x=-2 \text{ into the equation}. \\ y&=&-4-3 \qquad \quad \ \text{Perform the multiplication to clear the parenthesis}. \\ y&=&-7 \qquad \qquad \quad \text{Simplify the right side of the equation}. \end{array}\end{align*}$
::x2y=2x-3y=2-2-3Subtitution x2 进入方程式。y4-3 执行乘法清除括号。y7 简化方程式的右侧。

Repeat the process to calculate the values for the variable ‘ $\begin{align*}y\end{align*}$ .’
::重复计算变量“y.”的值的过程

\begin{aligned} \begin{array}{rcl} Given input value x & = & - 1 \\ y & = & 2 x - 3 \\ y & = & 2 (- 1) - 3 \\ y & = & - 2 - 3 \\ The output value is y & = & - 5 \end{array} \end{aligned}

$\begin{align*}\begin{array}{rcl} \text{Given input value }x&=&-1\\ y&=&2x-3\\ y&=&2(-1)-3\\ y&=&-2-3\\ \text{The output value is }y&=&-5 \end{array}\end{align*}$
::给定输入值 x% 1y= 2x- 3y= 2( - 1) - 3y}% 2 - 3 输出值为 y 5

\begin{aligned} \begin{array}{rcl} Given input value x & = & 0 \\ y & = & 2 x - 3 \\ y & = & 2 (0) - 3 \\ y & = & 0 - 3 \\ The output value is y & = & - 3 \end{array} \end{aligned}

$\begin{align*}\begin{array}{rcl} \text{Given input value }x&=&0\\ y&=&2x-3\\ y&=&2(0)-3\\ y&=&0-3\\ \text{The output value is }y&=&-3 \end{array}\end{align*}$
::给定输入值 x=0y=2x-3y=2(0)--3y=0- 3 输出值为 y3

\begin{aligned} \begin{array}{rcl} Given input value x & = & 1 \\ y & = & 2 x - 3 \\ y & = & 2 (1) - 3 \\ y & = & 2 - 3 \\ The output value is y & = & - 1 \end{array} \end{aligned}

$\begin{align*}\begin{array}{rcl} \text{Given input value }x&=&1\\ y&=&2x-3\\ y&=&2(1)-3\\ y&=&2-3\\ \text{The output value is }y&=&-1 \end{array}\end{align*}$
::给定输入值 x=1y=2x-3y=2(1)--3y=2- 3y=3 输出值为 y1

\begin{aligned} \begin{array}{rcl} Given input value x & = & 2 \\ y & = & 2 x - 3 \\ y & = & 2 (2) - 3 \\ y & = & 4 - 3 \\ The output value is y & = & 1 \end{array} \end{aligned}

$\begin{align*}\begin{array}{rcl} \text{Given input value }x&=&2\\ y&=&2x-3\\ y&=&2(2)-3\\ y&=&4-3\\ \text{The output value is }y&=&1 \end{array}\end{align*}$
::给定输入值 x=2y=2x- 3y=2 (2)--3y=4- 3 输出值为y=1

Write the calculated ‘ $\begin{align*}y\end{align*}$ ’ values in the table.
::在表格中写入计算中的 'y ' 值。

$\begin{align}x\end{align}$	$\begin{align}y\end{align}$
-2	-7
-1	-5
0	-3
1	-1
2	1

Plot the ordered pairs on the Cartesian grid and join the plotted points with a smooth, straight line.
::在笛卡尔网格上标定的一对配对,用平滑的直线加入绘图点。

Example 4
::例4

Plot the graph of the line having $\begin{align*}x=-2\end{align*}$ as its equation.
::绘制以 x2 为其方程的线条图。

First, remember this is the graph of one of the special lines.
::首先,请记住,这是其中一条特别线的图示。

Next, describe what the graph will look like.
::接下来,请描述图表的外观。

A vertical line passing through the point $\begin{align*}(-2,0)\end{align*}$ and parallel to the $\begin{align*}y\end{align*}$ -axis.
::垂直线穿过点(-2,0),与 Y 轴平行。

Then, graph the line on the Cartesian grid.
::然后在笛卡尔电网上绘制线条图

Example 5
::例5

Plot the graph of the line having $\begin{align*}y=-3\end{align*}$ as its equation.
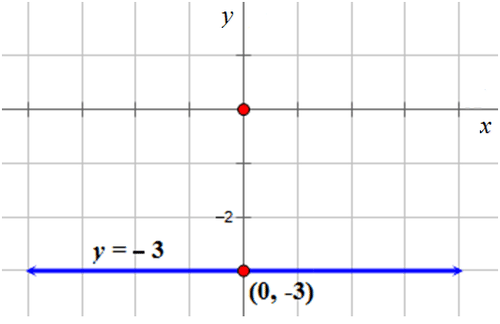
::绘制以 y3 为方程的线条图。

First, remember this is the graph of one of the special lines.
::首先,请记住,这是其中一条特别线的图示。

Next, describe what the graph will look like.
::接下来,请描述图表的外观。

A horizontal line passing through the point $\begin{align*}(0,-3)\end{align*}$ and parallel to the $\begin{align*}x\end{align*}$ -axis.
::水平线穿过点(0,-3),与 X 轴平行。

Then, graph the line on the Cartesian grid.
::然后在笛卡尔电网上绘制线条图

Review
::回顾

Create a table of values for each equation and then graph it on the coordinate plane.
::创建每个方程式的数值表,然后在坐标平面上绘制图表。

$\begin{align*}y = 2x + 1\end{align*}$
::y=2x+1 y=2x+1

$\begin{align*}y = 3x + 2\end{align*}$
::y=3x+2 y=3x+2

$\begin{align*}y = -4x\end{align*}$
::y4x

$\begin{align*}y = -2x\end{align*}$
::y2x

$\begin{align*}y =-3x + 3\end{align*}$
::y3x+3 y3x+3

$\begin{align*}y = 2x + 3\end{align*}$
::y=2x+3 y=2x+3

$\begin{align*}y = 3x- 2\end{align*}$
::y=3x-2

$\begin{align*}y =-8x\end{align*}$
::y8x

$\begin{align*}y = 3x + 1\end{align*}$
::y=3x+1 y=3x+1

$\begin{align*}y = 4x\end{align*}$
::y=4x y=4x

$\begin{align*}y = -2x + 2\end{align*}$
::y2x+2

$\begin{align*}y = 2x- 2\end{align*}$
::y=2x-2

$\begin{align*}y = x- 1\end{align*}$
::y=x-1

$\begin{align*}x = 4\end{align*}$
::x=4x=4

$\begin{align*}y = -2\end{align*}$
::y2

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

Section outline

Graphing Functions ::图图函数

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

Example 5 ::例5

Review ::回顾

Review (Answers) ::回顾(答复)