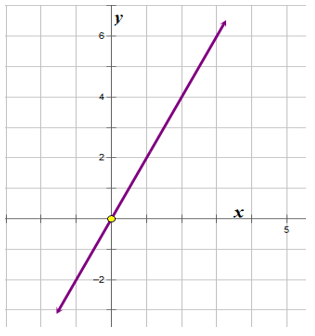Section: 直接和反反变化 | 9.8 直接和反反变化

Section outline

Kendall has to travel 240 miles to the city for a 3:00 pm. medical appointment and must take the bus. The bus travels at a rate of 60 miles per hour and leaves every hour on the hour. How can Kendall figure out which bus to take?
::肯德尔必须乘公交车,每小时60英里的路程,每小时离开。肯德尔怎么能确定要坐哪辆公交车?

In this concept, you will learn to understand direct and inverse variation .
::在这个概念中,你会学会理解直接和反向的变化。

Direct Variation
::直接变化

Direct and inverse variation are two different ways that show how one number changes with respect to another number. In , as one number increases, so does the other number. In other words, ‘ $\begin{align*}y\end{align*}$ ’ varies directly with ‘ $\begin{align*}x\end{align*}$ ’(or ‘ $\begin{align*}x\end{align*}$ ’ and ‘ $\begin{align*}y\end{align*}$ ’ are directly proportional). For example, there is a direct variation between the age and height. As the age of a child increases in years, the height of the child also increases. This example of direct variation can be expressed using the function $\begin{align*}y = k \cdot x\end{align*}$ such that $\begin{align*}x\end{align*}$ and $\begin{align*}y\end{align*}$ are the age and height of the child and ‘ $\begin{align*}k\end{align*}$ ’ is called the constant of proportionality . The constant of proportionality tells you how much ‘ $\begin{align*}y\end{align*}$ ’ will increase for every increase in ‘ $\begin{align*}x\end{align*}$ ’.
::直接的和反向的变异是两种不同的方式,表明一个数字相对于另一个数字是如何变化的。在一个数字中,随着一个数字的增加,另一个数字也随之增加。换句话说,“y”与`x ' (或`x ' 和`y”直接成比例。例如,年龄和身高之间有直接的差别。随着儿童年龄的岁数增加,孩子的身高也会增加。这个直接变异的例子可以用函数y=kx来表示,例如,x和y是孩子的年龄和身高,而`k ' 被称为相称的常数。比例的常数表明,在“x”每次增加时,“y”会增加多少。

Let’s look at an example.
::让我们举个例子。

\begin{aligned} y = 2 x \end{aligned}

$\begin{align*}y=2x\end{align*}$
::y=2x y=2x

The increase in $\begin{align*}y\end{align*}$ will equal twice the value of $\begin{align*}x\end{align*}$ . This can be clearly shown by creating a t-table.
::y的增量等于 x 的值的两倍。这可以通过创建table来清楚地显示。

\begin{aligned} \begin{array}{rcl} y & = & 2 x \\ y & = & 2 (1) \\ y & = & 2 \end{array} \end{aligned}

$\begin{align*}\begin{array}{rcl} y &=& 2x \\ y &=& 2(1) \\ y &=& 2 \end{array}\end{align*}$
::y=2xy=2(1)y=2

\begin{aligned} \begin{array}{rcl} y & = & 2 x \\ y & = & 2 (2) \\ y & = & 4 \end{array} \end{aligned}

$\begin{align*}\begin{array}{rcl} y &=& 2x \\ y &=& 2(2) \\ y &=& 4 \end{array}\end{align*}$
::y=2xy=2(2)y=4 y=4

\begin{aligned} \begin{array}{rcl} y & = & 2 x \\ y & = & 2 (3) \\ y & = & 6 \end{array} \end{aligned}

$\begin{align*}\begin{array}{rcl} y &=& 2x \\ y &=& 2(3) \\ y &=& 6 \end{array}\end{align*}$
::y=2xy=2(3)y=6 y=6

\begin{aligned} \begin{array}{rcl} y & = & 2 x \\ y & = & 2 (4) \\ y & = & 8 \end{array} \end{aligned}

$\begin{align*}\begin{array}{rcl} y &=& 2x \\ y &=& 2(4) \\ y &=& 8 \end{array}\end{align*}$
::y=2xy=2(4)y=8

$\begin{align}x\end{align}$	$\begin{align}y\end{align}$
1	2
2	4
3	6
4	8

Following is a graph of the direct variation equation $\begin{align*}y=2x\end{align*}$ .
::下面是直接变异方程式y=2x的图表。

Look at the above graph. The line passes through the origin $\begin{align*}(0,0)\end{align*}$ . If you think of the equation of a line written in slope-intercept form as $\begin{align*}y=mx+b\end{align*}$ then the equation of the given graph could be written as $\begin{align*}y=2x+0\end{align*}$ . This means the of the graphed line is 2.
::查看上图。线条通过源代码( 0,0) 。如果您将以斜度截面形式写成的线条的方程式 y=mx+b 视为y=mx+b, 则给定图的方程式可以写成 y= 2x+0 。这意味着图形线的方程式是 2 。

Inverse variation is the exact opposite of direct variation. In inverse variation , as one number increases, the other number decreases. If a student skips a lot of Advanced Math Classes then the mark on the exam will be low. The more classes skipped-the lower the mark. This example of inverse variation can be expressed using the function $\begin{align*}y=\frac{k}{x}\end{align*}$ such that $\begin{align*}x\end{align*}$ and $\begin{align*}y\end{align*}$ are the number of classes skipped and the lower math mark and ‘ $\begin{align*}k\end{align*}$ ’ is still called the constant of proportionality . In the equation $\begin{align*}y=\frac{k}{x}\end{align*}$ the constant ‘ $\begin{align*}k\end{align*}$ ’ is divided by the value of ‘ $\begin{align*}x\end{align*}$ ’. As the value of ‘ $\begin{align*}x\end{align*}$ ’ increases then the value of ‘ $\begin{align*}y\end{align*}$ ’ decreases.
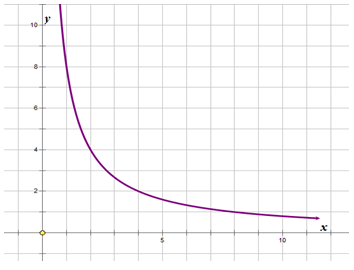
::反向变异是直接变异的正好相反。反向变异, 随着一个数字的增加, 另一个数字会减少。如果学生跳过许多高级数学课, 考试的分数会较低。更多的班会跳过分数, 分数越低。这个反向变异的例子可以用 y=kx 函数表示, 这样一来x 和 y 是跳过的班数, 低的数学分数和 ' k ' 仍然被称为相称性常数。在等式 y=kx 中, 常数 ' k ' 将除以 ' x ' 的值。随着 ' x ' 的值增加, y ' 的值将增加, y ' 减值。

The above graph shows an inverse variation. Notice how the value of ‘ $\begin{align*}y\end{align*}$ ’ gets smaller as the value of ‘ $\begin{align*}x\end{align*}$ ’ gets bigger.
::上图显示了反向变化。注意“ y” 值随着“ x” 值的增加而变小。

Examples
::实例

Example 1
::例1

Earlier, you were given a problem about Kendall and her medical appointment. She needs to figure out what time to get on the bus to get to her appointment on time. How can Kendall figure this out?
::早些时候,有人给了你一个关于肯德尔和她的医疗预约的问题。她需要弄清楚什么时候才能准时上公共汽车才能及时到达她的预约。肯德尔怎么才能弄清楚呢?

She can use the direct variation formula to figure out how long it will take her to get to the city on the bus.
::她可以使用直接变异公式来弄清楚她要多久才能搭公交车到达城市

First, write the equation for direct variation.
::首先,写出直接变异的方程。

\begin{aligned} y = k \cdot x \end{aligned}

$\begin{align*}y = k \cdot x\end{align*}$
::y=kx

Next, state the variables.
::接下来,请说明变量。

$\begin{align*}y=\end{align*}$ number of miles to travel
::y=旅行英里数

$\begin{align*}x=\end{align*}$ number of hours on the bus
::x=公共汽车上小时数

$\begin{align*}k=\end{align*}$ speed of the bus
::k=总线速度

Next, fill in $\begin{align*}k=60\end{align*}$ and $\begin{align*}y=240\end{align*}$ into the equation.
::下一步,在方程中填入 k=60 和 y= 240。

\begin{aligned} \begin{array}{rcl} y & = & k \cdot x \\ 240 & = & 60 \cdot x \\ 240 & = & 60 x \end{array} \end{aligned}

$\begin{align*}\begin{array}{rcl} y &=& k \cdot x \\ 240 &=& 60 \cdot x \\ 240 &=& 60 x \\ \end{array}\end{align*}$
::y=kx240=60x240=60x

Next, divide both sides of the equation by 60 to find the value of $\begin{align*}x\end{align*}$ .
::接下来,将方程两侧除以60,以找到x的值。

\begin{aligned} \begin{array}{rcl} 240 & = & 60 x \\ \frac{240}{60} & = & \frac{\overset{1}{60}}{60} x \\ 4 & = & x \end{array} \end{aligned}

$\begin{align*}\begin{array}{rcl} 240 &=& 60x \\ \frac{240}{60} &=& \frac{\overset{1}{\cancel{60}}}{\cancel{60}}x \\ 4 &=& x \end{array}\end{align*}$
::240=60x24060=60160x4=x

The answer is 4 hours on the bus.
::答案是,在公共汽车上4小时。

If Kendall’s appointment is at 3:00 p.m. and she will be on the bus for 4 hours, she can get on the 11:00 a.m. bus and arrive exactly on time. However, she might want to get on the bus that leaves at 10:00 a.m. to allow an hour for any unexpected delays in travel, like traffic.
::如果肯德尔的约会时间是下午3点,而且她会在公共汽车上停留4小时,她可以乘上午11点的公共汽车准时到达。但是,她可能想搭乘上午10点离开的公共汽车,以便有一个小时的旅行意外延误,比如交通。

Example 2
::例2

If $\begin{align*}y\end{align*}$ varies directly as $\begin{align*}x\end{align*}$ , and $\begin{align*}x=9\end{align*}$ when $\begin{align*}y=15\end{align*}$ , find $\begin{align*}y\end{align*}$ when $\begin{align*}x=33\end{align*}$ .
::如果 y 以 x 直接变化, 当 y= 15 时, x= 9 以 x = 33 直接变化, 则 x= 9 以 y 找到 y 。

First, write the equation for direct variation.
::首先,写出直接变异的方程。

\begin{aligned} y = k \cdot x \end{aligned}

$\begin{align*}y=k \cdot x\end{align*}$
::y=kx

Next, fill in $\begin{align*}x=9\end{align*}$ and $\begin{align*}y=15\end{align*}$ into the equation.
::下一个,以 x=9 和y=15 填入方程。

\begin{aligned} \begin{array}{rcl} y & = & k \cdot x \\ 15 & = & k \cdot 9 \\ 15 & = & 9 k \end{array} \end{aligned}

$\begin{align*}\begin{array}{rcl} y &=& k \cdot x\\ 15 &=& k \cdot 9 \\ 15 &=& 9k \end{array}\end{align*}$
::y=k*x15=k*915=9k y=k*x15=k*915=9k

Next, divide both sides of the equation by 9 to find the value of the constant of proportionality.
::其次,将等式的两边除以9,以找到相称性不变的价值。

\begin{aligned} \begin{array}{rcl} 15 & = & 9 k \\ \frac{15}{9} & = & \frac{\overset{1}{9}}{9} k \\ \frac{5}{3} & = & k \end{array} \end{aligned}

$\begin{align*}\begin{array}{rcl} 15 &=& 9k \\ \frac{15}{9} &=& \frac{\overset{1}{\cancel{9}}}{\cancel{9}}k \\ \frac{5}{3} &=& k \end{array}\end{align*}$
::15=9k159=919k53=k

Next, fill in the values $\begin{align*}k=\frac{5}{3}\end{align*}$ and $\begin{align*}x=33\end{align*}$ into the equation for direct variation to calculate the value of $\begin{align*}y\end{align*}$ .
::下一步,将 k=53 和 x=33 的值填入直接变异的方程,以计算y 的值。

\begin{aligned} \begin{array}{rcl} y & = & k \cdot x \\ y & = & \frac{5}{3} (33) \end{array} \end{aligned}

$\begin{align*}\begin{array}{rcl} y &=& k \cdot x\\ y &=& \frac{5}{3} (33) \end{array}\end{align*}$
::y=kxy=53(33)

Then, simplify the right side of the equation.
::然后,简化方程的右侧。

\begin{aligned} \begin{array}{rcl} y & = & \frac{5}{3} (\overset{11}{33}) \\ y & = & 5 (11) \\ y & = & 55 \end{array} \end{aligned}

$\begin{align*}\begin{array}{rcl} y &=& \frac{5}{\cancel{3}} \cancel{\left(\overset{11}{33}\right)} \\ y &=& 5(11) \\ y &=& 55 \end{array}\end{align*}$
::y=53( 3311y=5( 11y=55)

The answer is 55.
::答案是55岁

Example 3
::例3

The amount of money raised at a fundraiser is directly proportional to the number of people in attendance. If 5 people attending raised $100, then how much money will be raised if 60 people are in attendance?
::资金筹集者筹集的资金数额与与会人数成正比。如果有5人参加筹款者筹集了100美元,那么如果有60人参加,将筹集多少资金?

First, write the equation for direct variation.
::首先,写出直接变异的方程。

\begin{aligned} y = k \cdot x \end{aligned}

$\begin{align*}y=k \cdot x\end{align*}$
::y=kx

Next, state the variables.
::接下来,请说明变量。

$\begin{align*}y=\end{align*}$ amount of money raised
::y=筹集的资金数额

$\begin{align*}x=\end{align*}$ number of people in attendance
::x=出席人数

$\begin{align*}k=\end{align*}$ constant of proportionality
::k = 相称性不变

Next, fill in $\begin{align*}x=5\end{align*}$ and $\begin{align*}y=100\end{align*}$ into the equation.
::下一步,以 x=5 和 y=100 填入方程。

\begin{aligned} \begin{array}{rcl} y & = & k \cdot x \\ 100 & = & k \cdot 5 \\ 100 & = & 5 k \end{array} \end{aligned}

$\begin{align*}\begin{array}{rcl} y &=& k \cdot x\\ 100 &=& k \cdot 5 \\ 100 &=& 5k \end{array}\end{align*}$
::y=kx100=k5100=5k y=kx100=k5100=5k

Next, divide both sides of the equation by 5 to find the value of $\begin{align*}k\end{align*}$ .
::接下来,将方程两侧除以 5 以找到 k 的值。

\begin{aligned} \begin{array}{rcl} 100 & = & 5 k \\ \frac{100}{5} & = & \frac{\overset{1}{5}}{5} k \\ 20 & = & k \end{array} \end{aligned}

$\begin{align*}\begin{array}{rcl} 100 &=& 5k \\ \frac{100}{5} &=& \frac{\overset{1}{\cancel{5}}}{\cancel{5}}k \\ 20 &=& k \end{array}\end{align*}$
::100=5k1005=515k20=k

Next, fill in the values $\begin{align*}k=20\end{align*}$ and $\begin{align*}x=60\end{align*}$ into the equation for direct variation to calculate the value of $\begin{align*}y\end{align*}$ .
::下一步,将 k=20 和 x=60 的值填入直接变异的方程,以计算y 的值。

\begin{aligned} \begin{array}{rcl} y & = & k \cdot x \\ y & = & 20 (60) \end{array} \end{aligned}

$\begin{align*}\begin{array}{rcl} y &=& k \cdot x\\ y &=& 20(60) \end{array}\end{align*}$
::y=kxy=20( 60)

Then, simplify the right side of the equation.
::然后,简化方程的右侧。

\begin{aligned} \begin{array}{rcl} y & = & 20 (60) \\ y & = & 1200 \end{array} \end{aligned}

$\begin{align*}\begin{array}{rcl} y &=& 20(60) \\ y &=& 1200 \\ \end{array}\end{align*}$
::y=20( 60y=1200)

The answer is $1,200.
::答案是1200美元

Example 4
::例4

Dr. Burns told Katie the number of cavities she had in her teeth each year was inversely proportional to the number of minutes she spent brushing her teeth each time she brushed. If Katie had four new cavities during the year the time she spent each time brushing was only 30 seconds. How many new cavities will Katie have at the end of next year if she starts brushing for two minutes each time she brushes her teeth?
::伯恩斯医生告诉凯蒂,她每年牙洞的口腔数量与其每次刷牙时刷牙的分钟数成反比,如果凯蒂一年里有四个新的口腔,那么每次刷牙的时间只有30秒。

First, write the equation for inverse variation.
::首先,写反向变异的方程。

\begin{aligned} y = \frac{k}{x} \end{aligned}

$\begin{align*}y=\frac{k}{x}\end{align*}$
::y=kx y=kx

Next, state the variables.
::接下来,请说明变量。

$\begin{align*}y=\end{align*}$ number of new cavities
::y=新空洞的数量

$\begin{align*}x=\end{align*}$ number of minutes spent brushing
::x=用完刷刷的分钟数

$\begin{align*}k=\end{align*}$ constant of proportionality
::k = 相称性不变

Next, fill in $\begin{align*}x=0.5\end{align*}$ and $\begin{align*}y=4\end{align*}$ into the equation.
::下一个,以 x=0.5 和 y= 4 填入方程。

\begin{aligned} \begin{array}{rcl} y & = & \frac{k}{x} \\ 4 & = & \frac{k}{0.5} \end{array} \end{aligned}

$\begin{align*}\begin{array}{rcl} y &=& \frac{k}{x} \\ 4 &=& \frac{k}{0.5} \\ \end{array}\end{align*}$
::y=kx4=k0.5 y=kx4=k0.5

Next, multiply both sides of the equation by 0.5 to find the value of $\begin{align*}k\end{align*}$ .
::接下来,将方程的两边乘以0.5 以找到 k 的值。

\begin{aligned} \begin{array}{rcl} 4 & = & \frac{k}{0.5} \\ (0.5) 4 & = & \overset{1}{(0.5)} \frac{k}{0.5} \\ 2 & = & k \end{array} \end{aligned}

$\begin{align*}\begin{array}{rcl} 4 &=& \frac{k}{0.5} \\ (0.5)4 &=& \overset{1}{\cancel{(0.5)}} \frac{k}{\cancel{0.5}}\\ 2 &=& k \end{array}\end{align*}$
::4=k0.5(0.5)4=(0.5)1k0.52=k

Next, fill in the values $\begin{align*}k=2\end{align*}$ and $\begin{align*}x=2\end{align*}$ into the equation for inverse variation to calculate the value of $\begin{align*}y\end{align*}$ .
::下一步,在公式中填入 k=2 和 x=2 的值,以进行反向变异,以计算y 的值。

\begin{aligned} \begin{array}{rcl} y & = & \frac{k}{x} \\ y & = & \frac{2}{2} \\ y & = & 1 \end{array} \end{aligned}

$\begin{align*}\begin{array}{rcl} y &=& \frac{k}{x} \\ y &=& \frac{2}{2} \\ y &=& 1 \end{array}\end{align*}$
::y=kxy=22y=1

The answer is 1 new cavity.
::答案是1个新的洞穴。

Example 5
::例5

Margie was going on a trip and was travelling at a speed of 50 miles per hour. As the number of hours travelling increased so did the distance she travelled. Is this an example of direct or inverse variation? Explain your answer.
::Margie当时旅行时速为每小时50英里,旅行时数增加,旅行时数增加,她旅行的距离也增加,这是直接或反向变化的例子吗?解释你的答复。

As the time travelling increased, the number of miles travelled increased. This is an example of direct variation which says as the value of one quantity increases so does the value of the other quantity
::随着旅行时间的增加,旅行的里程数增加,这是直接变化的一个实例,表明一个数量增加的价值,另一个数量的价值也是如此。

Review
::回顾

State whether each situation described is an example of direct variation or inverse variation.
::说明所描述的每一种情况是直接变异还是反向变异的例子。

1. The train traveled at a speed of 80 miles per hour. The number of miles increased with every hour that the train was running.
::1. 火车以每小时80英里的速度行驶,每小时行驶,英里数随车时数的增加而增加。

2. The train traveled at a speed of 80 miles per hour, then it increased it’s speed. The number of hours on the train decreased with the increase in speed.
::2. 火车以每小时80英里的速度行驶,然后加快速度,随着速度的加快,列车时数减少。

3. Mary is training for a marathon. She runs many hours each week. After a few weeks of running, she noticed that her speed increased.
::3. Mary正在训练马拉松,每周运行许多小时,经过几个星期的跑步后,她注意到她的速度加快了。

4. Kevin has been working for the same company for several years. He has received a raise each year that he has been with the company.
::4. Kevin为同一家公司工作了几年,他每年在该公司工作一次,每年得到加薪。

5. Joseph has been working for the same company too, but his salary has decreased each year.
::5. Joseph也在同一家公司工作,但他的工资每年下降。

6. Kelly spent more hours studying than she ever had before. She was surprised when she received a lower score on this test than she had on any previous tests.
::6. Kelly学习的时间比以前多,在考试得分低于以前任何考试得分时,她感到惊讶。

7. Jeff is on a diet. He knows that the number of calories that he burns is directly connected with the number of hours that he exercises.
::7. Jeff正在节食,他知道他烧伤的卡路里数量与他练习的小时数直接相关。

8. Seth and Sarah spent a lot of time eating while they were on vacation. After vacation was over, they both noticed that they had each gained five pounds.
::8. Seth和Sarah在休假期间经常吃东西,假期结束后,他们都注意到每人增加了5磅。

9. Mary’s training has increased. She has been keeping track of how long it takes her to run 1 mile. She noticed that the she trained, the faster her time became.
::9. 玛丽的训练有所增加,她一直在跟踪她跑1英里需要多长时间,她注意到她训练的时间越快,她的时间就越快。

10. Over time, the price of a postage stamp has increased a few pennies each year.
::10. 随着时间推移,邮票价格每年增加几分钱。

Answer each question true or false.
::回答每个问题是否真实或虚假。

11. In direct variation, one factor increases as the other factor increases.
::11. 在直接变化中,一个因素随着其他因素的增加而增加。

12. In inverse variation, one factor increases, but the other factor decreases.
::12. 反向变化,一个因素增加,但另一个因素减少。

13. When you see the letter k in a situation, you can think of a constant variable.
::13. 当看到K字母在某种情况下时,可以想到一个不变变量。

14. If a plane ascends and then quickly descends, this is an example of direct variation.
::14. 如果飞机上升,然后迅速下降,这是直接变化的例子。

15. If your exercise increases and you lose weight, then this is an example of direct variation.
::15. 如果锻炼增加而体重减低,这就是直接变化的例子。

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

Section outline

Direct Variation ::直接变化

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

Example 5 ::例5

Review ::回顾

Review (Answers) ::回顾(答复)

Direct Variation
::直接变化

Examples
::实例

Example 1
::例1

Example 2
::例2

Example 3
::例3

Example 4
::例4

Example 5
::例5

Review
::回顾

Review (Answers)
::回顾(答复)