节: 使用合并名称评价合并 | 11.6 利用合并名称评价合并情况

章节大纲

Mauricio is waiting in line at the ice cream truck. There are nine different toppings available, and Mauricio has enough money to get two, but he can’t decide which two toppings to choose. How many different selections can Mauricio make?
::Mauricio正在冰淇淋卡车排队等候。有九种不同的托盘可用,毛里西奥有足够的钱买两只,但他无法决定选择哪两只托盘。 Mauricio可以选择多少种不同的选择?

In this concept, you will learn to use combination notation to evaluate combinations.
::在此概念中,您将学会使用组合符号来评价组合。

Combination
::合并

Order is important for some groups of items but not important for others. Consider a list of the words: POTS, STOP, SPOT, and TOPS.
::顺序对某些组项目很重要, 但对其他组项目并不重要。考虑一个单词列表 : POTS、 STOP、 SPOT 和 TAPS 。

For the spelling of each individual word, order is important. The words POTS, STOP, SPOT, and TOPS all use the same letters, but spell out very different words.
::对于每个单词的拼写,顺序很重要。 POTS、STOP、SPOT和TOPS等词都使用相同的字母,但用非常不同的词来表达。

For the list itself, order is not important. Whether the words are presented in one order –such as POTS, STOP, SPOT, TOPS, or another order, such as STOP, SPOT, TOPS, POTS, or a third order, such as TOPS, POTS, SPOT, and STOP -makes no difference. As long as the list includes all 4 words, the order of the 4 words doesn’t matter.
::对清单本身来说,顺序并不重要。无论单词是按一个顺序排列的 — — 比如POTS,STOP,SPOT,TOPS,或者其他顺序,比如STOP,SPOT,TOPS,POTS,或第三顺序,比如TOPS,POT,SPOT和STOP — — 都没有区别。只要列表包括所有四个单词,4个单词的顺序就无关紧要了。

A is an arrangement of items in which order, or how the items are arranged, is not important. The collection of one order of the items is not functionally different than any other order.
::A 是一种项目安排,其顺序或项目安排方式并不重要,项目的一个顺序的收集在功能上与任何其他顺序并无不同。

When evaluating a combination, you can use a tree diagram . Use a tree diagram can be time consuming; combination notation is a much simpler option.
::在评价组合时,您可以使用树图。使用树图可以耗时;组合符号是一个简单得多的选择。

To use combination notation, you must first understand . A is a special number that represents the product of a set of values in descending order.
::要使用组合符号, 您必须首先理解。 A 是一个特殊的数字, 以降序表示一组数值的产物。

Let’s look at an example of a factorial evaluation.
::让我们看看一个因素评估的例子。

Evaluate $\begin{align*}5!\end{align*}$ .
::评估5!

You can say that this is the product of values starting with 5 in descending order.
::你可以说这是数值的产物从5开始按降序从5开始。

$\begin{aligned} \begin{array}{rcl} 5! & = & 5 \times 4 \times 3 \times 2 \times 1 \\ = & 120 \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} 5! &=& 5 \times 4 \times 3 \times 2 \times 1 \\ &=&120 \\ \end{array}\end{align*}$

The answer is 120.
::答案是120个

You can use factorials and combination notation to evaluate combinations without using lists or .
::您可以使用乘数和组合符号来评价组合,而不使用列表或。

Let’s take a look at how this works.
::让我们看看这如何运作。

To represent the number of combinations there are for 6 items taken 4 at a time, use the notation $\begin{align*}{\color{red}_6}C{\color{blue}_4}.\end{align*}$
::为表示组合数,6个项目的组合数,每次4个,使用编号6C4。

In general, combinations are written as:
::一般说来,组合的写法是:

$\begin{aligned} _{n} C_{r} \end{aligned}$
$\begin{align*}{\color{red}_n}C{\color{blue}_r}\end{align*}$
::nCr/ nCr

where $\begin{align*}{\color{red}n}\end{align*}$ items are taken $\begin{align*}{\color{blue}r}\end{align*}$ at a time.
::n项是一次拍摄r项。

To compute $\begin{align*} _nC_r\end{align*}$ use the formula:
::要计算 nCr 使用公式:

$\begin{aligned} _{n} C_{r} = \frac{n!}{r! (n - r)!} \end{aligned}$
$\begin{align*}_nC_r = \frac{n!}{r!(n-r)!}\end{align*}$
::Nrn! r! ! ! r! r! r! ! ! !

Let’s look at an example.
::让我们举个例子。

Find $\begin{align*}_5C_2\end{align*}$
::查找 5C2

First, set up the problem.
::首先,设置问题。

$\begin{aligned} \begin{array}{rcl} _{n} C_{r} = \frac{n!}{r! (n - r)!} \\ _{5} C_{2} = \frac{5!}{2! (5 - 2)!} \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} _nC_r = \frac{n!}{r!(n-r)!} \\ _5C_2 = \frac{5!}{2!(5-2)!} \\ \end{array}\end{align*}$
::5C2=5! 2! (5 -2)!

Next, evaluate the expression.
::接下来,评价表达式。

$\begin{aligned} \begin{array}{rcl} _{5} C_{2} & = & \frac{5!}{2! (5 - 2)!} \\ _{5} C_{2} & = & \frac{5!}{2! (3)!} \\ _{5} C_{2} & = & \frac{5 \times 4 \times 3 \times 2 \times 1}{2 \times 1 (3 \times 2 \times 1)} \\ _{5} C_{2} & = & \frac{5 \times 4}{2 \times 1} \\ _{5} C_{2} & = & \frac{20}{2} \\ _{5} C_{2} & = & 10 \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} _5C_2 &=& \frac{5!}{2!(5-2)!} \\ _5C_2 &=& \frac{5!}{2!(3)!} \\ _5C_2 &=& \frac{5 \times 4 \times 3 \times 2 \times 1}{2 \times 1(3 \times 2 \times 1)} \\ _5C_2 &=&\frac{5 \times 4}{2 \times 1} \\ _5C_2 &=&\frac{20}{2} \\ _5C_2 &=&10 \\ \end{array}\end{align*}$
::5C2=5! 2!! (5-2)! 5C2=5! 2! (3)! 5C2=5x4x4x3x3x2x12x1(3x2x2x1) 5C2=5x42x15C2=2025C2=10

The answer is 10.
::答案是10个

There are 10 combinations.
::有10个组合。

You can also use a graphing calculator to find combinations. For large numbers, especially, the calculator can save you time.
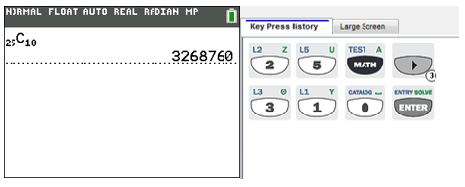
::您也可以使用图形计算器来查找组合。对于大数字,特别是对于大数字,计算器可以节省时间。

If you push the “m” button and on the top of the screen you will see PROB. #3 under the PROB menu is combinations.
::如果您按下“ m” 按钮并在屏幕上方, 您将会看到 PROB 。在 PROB 菜单下, # 3 是组合。

Let’s try an example.
::让我们以身作则。

Find $\begin{align*}_{25}C_{10}\end{align*}$ using your calculator. Notice the key press history to help you with the keystrokes.
::使用计算器查找 25C10。注意密钥按键历史可以帮助您执行按键。

The answer is 3,268,760.
::答案是3,268,760

Examples
::实例

Example 1
::例1

Earlier, you were given a problem about Mauricio and his toppings.
::早些时候,你被问及Mauricio和他的脚趾的问题。

Mauricio has to choose two ice cream toppings from nine different toppings available. How many different combinations can he choose?
::Mauricio必须选择9种不同的冰淇淋药片中的2种冰淇淋药片。他可以选择多少种不同的配方?

First, write the combination notation to describe the situation.
::首先,写上组合符号来描述情况。

$\begin{aligned} _{9} C_{2} \end{aligned}$
$\begin{align*}_9C_2\end{align*}$
::9C2

Next, set up the problem.
::下一个,设置问题。

$\begin{aligned} \begin{array}{rcl} _{n} C_{r} & = & \frac{n!}{r! (n - r)!} \\ _{9} C_{2} & = & \frac{9!}{2! (9 - 2)!} \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} _nC_r &=& \frac{n!}{r!(n-r)!} \\ _9C_2 &=& \frac{9!}{2!(9-2)!} \\ \end{array}\end{align*}$
::NC=n! r! ! 9C2=9! 2! (9-2)!

Then, evaluate the expression.
::然后,评估表达方式。

$\begin{aligned} \begin{array}{rcl} _{9} C_{2} & = & \frac{9!}{2! (9 - 2)!} \\ _{9} C_{2} & = & \frac{9!}{2! (7)!} \\ _{9} C_{2} & = & \frac{9 \times 8 \times 7 \times 6 \times 5 \times 4 \times 3 \times 2 \times 1}{2 \times 1 \times (7 \times 6 \times 5 \times 4 \times 3 \times 2 \times 1)} \\ _{9} C_{2} & = & \frac{9 \times 8}{2 \times 1} \\ _{9} C_{2} & = & \frac{72}{2} \\ _{9} C_{2} & = & 36 \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} _9C_2 &=& \frac{9!}{2!(9-2)!} \\ _9C_2 &=& \frac{9!}{2!(7)!} \\ _9C_2 &=& \frac{9\times 8\times 7\times 6\times 5 \times 4 \times 3 \times 2 \times 1}{2 \times 1 \times (7 \times 6\times 5\times 4\times 3 \times 2 \times 1)} \\ _9C_2 &=&\frac{9 \times 8 }{2 \times 1} \\ _9C_2 &=&\frac{72}{2}\\ _9C_2 &=&36\\ \end{array}\end{align*}$
::9C2=9!2!9C2=9!2!9C2=9!2!(7)!9C2=9x8x8x7x6x5xx4x4x3x3x2x12x1xx7x65x4x3x3x3x2x1x9C2=9x8219C2=7229C2=36

The answer is 36.
::答案是36岁

There are 36 different combinations of two toppings.
::有36种不同的组合两种托普。

Example 2
::例2

Write the following situation using combination notation. Then evaluate it.
::使用组合符号写下以下情形。然后评估它。

Sixteen students went to the park. Four students could ride in four cars. How many different combinations of students could there be?
::16名学生去了公园,4名学生可以乘坐4辆汽车。

First, use combination notation to describe the problem.
::首先,使用混合符号来描述问题。

Find $\begin{align*}_{16}C_4\end{align*}$
::查找 16C4

Next, evaluate the combination by simplifying first.
::接下来,首先通过简化来评估组合。

$\begin{aligned} \begin{array}{rcl} _{n} C_{r} & = & \frac{n!}{r! (n - r)!} \\ _{16} C_{4} & = & \frac{16!}{4! (16 - 4)!} \\ _{16} C_{4} & = & \frac{16!}{4! (12)!} \\ _{16} C_{4} & = & \frac{16 \times 15 \times 14 \times 13 \times 12 \times 11 \times 10 \times 9 \times 8 \times 7 \times 6 \times 5 \times 4 \times 3 \times 2 \times 1}{4 \times 3 \times 2 \times 1 \times (12 \times 11 \times 10 \times 9 \times 8 \times 7 \times 6 \times 5 \times 4 \times 3 \times 2 \times 1)} \\ _{16} C_{4} & = & \frac{16 \times 15 \times 14 \times 13}{4 \times 3 \times 2 \times 1} \\ _{16} C_{4} & = & \frac{43680}{24} \\ _{16} C_{4} & = & 1820 \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} _nC_r &=& \frac{n!}{r!(n-r)!} \\ _{16}C_4 &=& \frac{16!}{4!(16-4)!} \\ _{16}C_4 &=& \frac{16!}{4!(12)!} \\ _{16}C_4 &=& \frac{16\times 15\times 14\times 13\times 12\times 11 \times 10\times 9 \times 8 \times 7\times 6\times 5\times 4\times 3\times 2\times 1}{4\times 3\times 2\times 1 \times (12\times 11 \times 10\times 9 \times 8 \times 7\times 6\times 5\times 4\times 3\times 2\times 1)} \\ _{16}C_4 &=& \frac{16\times 15\times 14\times 13}{4\times 3\times 2\times 1} \\ _{16}C_4 &=&\frac{43680}{24} \\ _{16}C_4 &=&1820 \\ \end{array}\end{align*}$
::nCr=n! r! (n- r) ! 16C4=16! 4! (16- 4) 16C4=16! ! (12) 16C4=16! ! (16) 16C4=16! 4! (12) 16C4=16x15xxx14x 14x13x13x13x13x13x13x13xx1211xx10x199x8x7x7xx65}}}x3x2x2x14x14x14x14x134x3xxxx16C4=436802416C4=1820

The answer is 1,820.
::答案是1,820

There are 1820 different combinations.
::有1820种不同的组合。

Example 3
::例3

Find $\begin{align*}_6C_3.\end{align*}$
::查找 6C3 。

First, set up the problem.
::首先,设置问题。

$\begin{aligned} \begin{array}{rcl} _{n} C_{r} & = & \frac{n!}{r! (n - r)!} \\ _{6} C_{3} & = & \frac{6!}{3! (6 - 3)!} \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} _nC_r &=& \frac{n!}{r!(n-r)!} \\ _6C_3 &=& \frac{6!}{3!(6-3)!} \\ \end{array}\end{align*}$
::6C3=6! 3! (6 -3)!

Next, evaluate the expression.
::接下来,评价表达式。

$\begin{aligned} \begin{array}{rcl} _{6} C_{3} & = & \frac{6!}{3! (6 - 3)!} \\ _{6} C_{3} & = & \frac{6!}{3! (3)!} \\ _{6} C_{3} & = & \frac{6 \times 5 \times 4 \times 3 \times 2 \times 1}{3 \times 2 \times 1 \times (3 \times 2 \times 1)} \\ _{6} C_{3} & = & \frac{6 \times 5 \times 4}{3 \times 2 \times 1} \\ _{6} C_{3} & = & \frac{120}{6} \\ _{6} C_{3} & = & 20 \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} _6C_3 &=& \frac{6!}{3!(6-3)!} \\ _6C_3 &=& \frac{6!}{3!(3)!} \\ _6C_3 &=& \frac{6 \times 5 \times 4 \times 3 \times 2 \times 1}{3\times 2\times 1\times (3\times 2\times 1)}\\ _6C_3 &=& \frac{6\times 5 \times4}{3\times 2\times 1} \\ _6C_3 &=& \frac{120}{6} \\ _6C_3 &=& 20 \\ \end{array}\end{align*}$
::6C3=6!3! (6- 3) ! 6C3=6! 3! (3)!! 6C3=6C3=6x5x5x4x4x3x3xx2x23x13x13x2x2x1x(3x2x2x1) 6C3=6x5x5x43xx2x16C3=12066C3=20

The answer is 20.
::答案是20岁

There are 20 combinations.
::有20个组合。

Example 4
::例4

Find $\begin{align*}_9C_3.\end{align*}$
::找9C3,发现9C3。

First, set up the problem.
::首先,设置问题。

$\begin{aligned} \begin{array}{rcl} _{n} C_{r} & = & \frac{n!}{r! (n - r)!} \\ _{9} C_{3} & = & \frac{9!}{3! (9 - 3)!} \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} _nC_r &=& \frac{n!}{r!(n-r)!} \\ _9C_3 &=&\frac{9!}{3!(9-3)!} \\ \end{array}\end{align*}$
::NC3=9,3,9C3=9,9C3!

Next, evaluate the expression.
::接下来,评价表达式。

$\begin{aligned} \begin{array}{rcl} _{9} C_{3} & = & \frac{9!}{3! (9 - 3)!} \\ _{9} C_{3} & = & \frac{9!}{3! (6)!} \\ _{9} C_{3} & = & \frac{9 \times 8 \times 7 \times 6 \times 5 \times 4 \times 3 \times 2 \times 1}{3 \times 2 \times 1 \times (6 \times 5 \times 4 \times 3 \times 2 \times 1)} \\ _{9} C_{3} & = & \frac{9 \times 8 \times 7}{3 \times 2 \times 1} \\ _{9} C_{3} & = & \frac{504}{6} \\ _{9} C_{3} & = & 84 \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} _9C_3 &=& \frac{9!}{3!(9-3)!} \\ _9C_3 &=& \frac{9!}{3!(6)!} \\ _9C_3 &=& \frac{9\times 8\times 7\times 6\times 5 \times 4 \times 3 \times 2 \times 1}{3 \times2 \times 1 \times (6\times 5\times 4\times 3 \times 2 \times 1)} \\ _9C_3 &=&\frac{9 \times 8 \times 7}{3 \times 2 \times 1} \\ _9C_3 &=&\frac{504}{6} \\ _9C_3 &=&84 \end{array}\end{align*}$
::9C3=9!3!9C3=9!3!6!9C3=9!3!(6)!9C3=9x8x8x7x6x5x5x4x4x3x3x2x13x2x2x1xxx6x6x5x4x4x3x3x3x2x1x9C3=9x8x73x23x19C3=50469C3=84

The answer is 84.
::答案是84

There are 84 combinations.
::有84个组合。

Example 5
::例5

Find $\begin{align*}_5C_4\end{align*}$ .
::找5C4 找5C4 找5C4 找5C4 找5C4 Find 5C4.

First, set up the problem.
::首先,设置问题。

$\begin{aligned} \begin{array}{rcl} _{n} C_{r} & = & \frac{n!}{r! (n - r)!} \\ _{5} C_{4} & = & \frac{5!}{4! (5 - 4)!} \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} _nC_r&=& \frac{n!}{r!(n-r)!} \\ _5C_4 &=&\frac{5!}{4!(5-4)!} \\ \end{array}\end{align*}$
::{\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}不! {\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}不! {\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}不! {\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}不!

Next, evaluate the expression.
::接下来,评价表达式。

$\begin{aligned} \begin{array}{rcl} _{5} C_{4} & = & \frac{5!}{4! (5 - 4)!} \\ _{5} C_{4} & = & \frac{5!}{4! (1)!} \\ _{5} C_{4} & = & \frac{5 \times 4 \times 3 \times 2 \times 1}{4 \times 3 \times 2 \times 1 \times (1)} \\ _{5} C_{4} & = & \frac{5}{1} \\ _{5} C_{4} & = & 5 \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} _5C_4 &=&\frac{5!}{4!(5-4)!} \\ _5C_4&=& \frac{5!}{4!(1)!} \\ _5C_4 &=& \frac{5 \times 4 \times 3 \times 2 \times 1} {4\times 3 \times2 \times 1 \times (1)} \\ _5C_4 &=&\frac{5}{1}\\ _5C_4 &=&5\\ \end{array}\end{align*}$
::5C4=5! 5C4=5! 4! 1! 5C4=5C4! 1! 5C4=5C4=5! 1! 5C4=5x4x4x3x3x3x2x14x3x3x3x2x1x1x1x1x5C4=515C4=5

The answer is 5.
::答案是5。

There are 5 combinations.
::有五种组合。

Review
::回顾

Evaluate each combination.
::评估每种组合。

1. Find $\begin{align*}_5C_2\end{align*}$
::1. 找 5C2

2. Find $\begin{align*}_6C_5\end{align*}$
::2. 找 6C5

3. Find $\begin{align*}_7C_2\end{align*}$
::3. 参见7C2

4. Find $\begin{align*}_7C_3\end{align*}$
::4. 查找7C3

5. Find $\begin{align*}_8C_2\end{align*}$
::5. 查找8C2

6. Find $\begin{align*}_6C_4\end{align*}$
::6. 查找 6C4

7. Find $\begin{align*}_9C_2\end{align*}$
::7. 查获9C2

8. Find $\begin{align*}_9C_4\end{align*}$
::8. 查获9C4

9. Find $\begin{align*} _8C_3\end{align*}$
::9. 查找8C3

10. Find $\begin{align*}_4C_4\end{align*}$
::10. 查找 4C4

Use the formula to figure out the different combinations.
::使用公式来计算不同的组合。

11. How many different color pairs are there among red, orange, yellow, green, and blue?
::11. 红色、橙色、黄色、绿色和蓝色之间有多少不同的颜色配对?

12. How many different sets of 3 colors are there among red, orange, yellow, green, and blue?
::12. 红色、橙色、黄色、绿色和蓝色之间有多少套不同的3种颜色?

13. How many different color pairs are there among red, orange, yellow, green, blue, and purple?
::13. 红色、橙色、黄色、绿色、绿色、蓝色和紫色之间有多少不同的颜色配对?

14. How many different sets of 3 colors are there among red, orange, yellow, green, blue, and purple?
::14. 红色、橙色、黄色、绿色、蓝色和紫色之间有多少三种不同的颜色?

15. How many different sets of 3 colors are there among red, orange, yellow, green, blue, purple, and white?
::15. 红色、橙色、黄色、绿色、绿色、蓝色、紫色和白色之间有多少三种不同的颜色?

16. Ten tennis players are on the Davis Cup Team. Only two players can play in the doubles finals. How many different doubles teams could play in the finals?
::16. 戴维斯杯队有10名网球运动员,只有2名球员可以参加双人决赛,决赛中可以参加多少个不同的双人球队?

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

Resources
::资源

章节大纲

Combination ::合并

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

Example 5 ::例5

Review ::回顾

Review (Answers) ::回顾(答复)

Resources ::资源

Combination
::合并

Examples
::实例

Example 1
::例1

Example 2
::例2

Example 3
::例3

Example 4
::例4

Example 5
::例5

Review
::回顾

Review (Answers)
::回顾(答复)

Resources
::资源