指数增长和衰减

播放段落

A condominium complex charges $185 per month for the homeowners’ association fee. The rates can rise every year because of inflation but they promise not to raise the rates more than 10% each year. Keep in mind, though, that if they raise the rate by 10% the first year, the second year is now more expensive. If they raise the maximum again, they are increasing the original $185 plus the first year’s adjustment by 10%. Graph the situation for 10 years.
::公寓综合体每月收费185美元,以支付房主协会费。 利率可以因通货膨胀而逐年上涨,但保证利率不会每年提高10 % 。 但是,记住,如果第一年将利率提高10 % , 第二年现在更昂贵。 如果他们再次提高最高利率,则将原来的185美元加第一年的调整增加10 % 。 分析10年的情况。

播放段落

How much could the homeowners’ fee be in ten years? Use the function $\begin{array}{r}f=185\times {1.1}^t\end{array}$  where $\begin{array}{r}f\end{array}$  is the fee after  $\begin{array}{r}t\end{array}$  years.
::10年内房主的收费能有多少?使用这个功能f=185x1.1t,f是年之后的收费。

播放段落

In this concept, you will learn to distinguish between and .
::在这一概念中,你会学会区分和区分。

播放段落

Exponential Growth and Decay
::指数增长和衰减

播放段落

Sometimes you will need to identify whether a function is an exponential function . If your function can be written in the form $\begin{array}{r}y=a{b}^x\end{array}$ , where $\begin{array}{r}a\end{array}$  and $\begin{array}{r}b\end{array}$  are constants, $\begin{array}{r}a\ne 0,b>0\end{array}$  , and $\begin{array}{r}b\ne 1\end{array}$  , then it must be exponential. In quadratic equations, your functions were always to the 2 ^nd power. In , the exponent is a variable . Their graphs will have a characteristic curve either upward or downward.
::有时您需要确定函数是否是一个指数函数。 如果您的函数可以以 y=abx 的形式写成, 其中 a和 b 是常数, a0, b>0, 和 b1, 那么它必须是指数。 在二次方程式中, 您的函数总是在第二倍。 在 中, 引号是一个变量。 它们的图表将有一个向上或向下的特性曲线 。

播放段落

Therefore the function  $\begin{array}{r}c=4\times {10}^a\end{array}$  is an exponential function, but   $\begin{array}{r}y=-6\times 0^x\end{array}$  is not because $\begin{array}{r}b\le 1\end{array}$ .
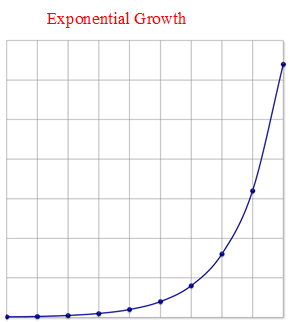
::因此,函数 c=4x10a 是一个指数函数,但 y=6x0x 不是因为 b1 。

播放段落

In some cases with exponential functions, as the $\begin{array}{r}x\end{array}$  value increased, the $\begin{array}{r}y\end{array}$  value increased, too. This was a direct relationship known as exponential growth . As the $\begin{array}{r}x\end{array}$  value increases, the $\begin{array}{r}y\end{array}$  value grows at a very fast rate!
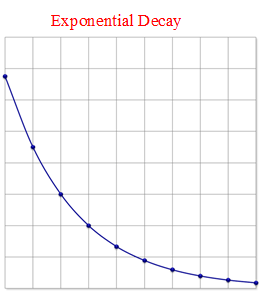
::在某些具有指数函数的情况下, 随着 x 值的增加, y 值也增加了。 这是直接的关系, 被称为指数增长 。 随着 x 值的增加, y 值以非常快的速度增长 !

播放段落

In other cases, as the $\begin{array}{r}x\end{array}$  value increased, the $\begin{array}{r}y\end{array}$  value decreased. This relationship is an inverse relationship known as exponential decay . The graphs of these functions are opposites, reflected on the $\begin{array}{r}y\end{array}$ -axis.
::在其他情况下,随着 x 值的增加, Y 值下降。 此关系是一种反向关系, 被称为指数衰减。 这些函数的图形是相反的, 反映在 Y 轴上 。

 

播放段落

Examples
::实例

播放段落

Example 1
::例1

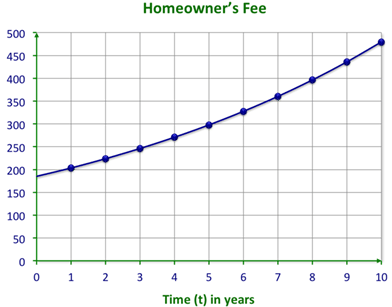
播放段落

Earlier, you were given a problem about  the rising condominium fees. You need to determine how much the homeowners’ fee will be in ten years using the function $\begin{array}{r}f=185\times {1.1}^t\end{array}$  where $\begin{array}{r}f\end{array}$  is the fee after $\begin{array}{r}t\end{array}$  years.
::早些时候,您曾遇到有关公寓费上涨的问题。 您需要使用 F=185x1.1t 的功能来决定十年内房主费的多少, F 是 T 年之后的f 收费 。

播放段落

First, make a table of values for the function $\begin{array}{r}f=185\times {1.1}^x\end{array}$  .
::首先,绘制函数 f=185x1.1x 的值表。

$\begin{array}{r}t\end{array}$	0	1	2	3	4	5	6	7	8
$\begin{array}{r}f\end{array}$	185	203.50	223.85	246.24	270.86	297.94	327.74	360.51	396.56

播放段落

Next, graph the function.
::下一位, 绘制函数图 。

播放段落

Example 2
::例2

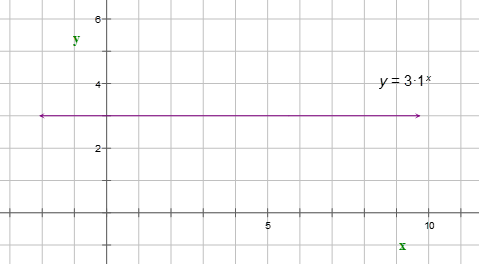
播放段落

Does the following function represent an exponential function? Graph the function.
::以下函数是否代表指数函数?图形显示函数。

播放段落

::y=3x1x y=3x1x

播放段落

First, answer the question.
::首先,回答问题。

播放段落

No, this function does not represent an exponential function because the $\begin{array}{r}b\end{array}$  value is 1.
::否,此函数不代表指数函数,因为 b 值为 1。

播放段落

Next, graph the function.
::下一位, 绘制函数图 。

播放段落

Example 3
::例3

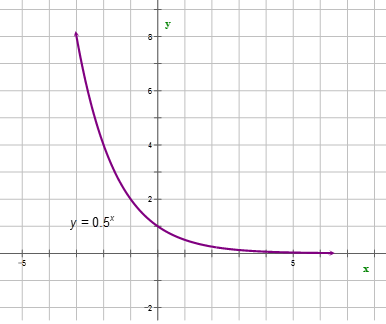
播放段落

Graph the function $\begin{array}{r}y={\left(\frac{1}{2}\right)}^x\end{array}$  and tell whether it will represent exponential growth or decay.
::绘制函数y=( 12) x 的图, 并显示它代表指数增长还是衰变 。

播放段落

First, graph the function.
::首先,绘制函数图。

播放段落

Next, answer the question.
::下一个,回答问题。

播放段落

From the graph, the function $\begin{array}{r}y={\left(\frac{1}{2}\right)}^x\end{array}$  represents exponential decay.
::从图形中,函数 y=( 12)x 表示指数衰减。

播放段落

Example 4
::例4

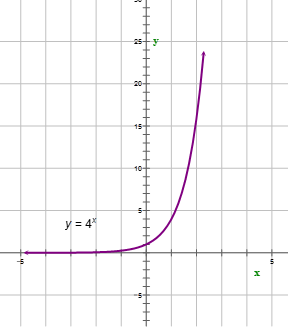
播放段落

Graph the function $\begin{array}{r}y=4^x\end{array}$  and tell whether it represents exponential growth or decay.
::绘制 y= 4x 函数图,并显示该函数代表指数增长还是衰变。

播放段落

First, graph the function.

::首先,绘制函数图。

播放段落

Next, answer the question.
::下一个,回答问题。

播放段落

From the graph, the function $\begin{array}{r}y=4^x\end{array}$  represents exponential growth.
::从图中,函数y=4x代表指数增长。

播放段落

Example 5
::例5

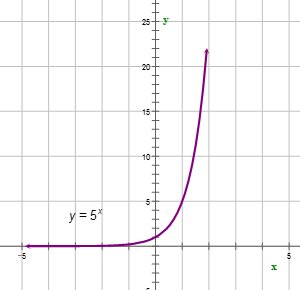
播放段落

Graph the function $\begin{array}{r}y=5^x\end{array}$  and tell whether it represents exponential growth or decay.
::绘制 y= 5x 函数图,并显示该函数代表指数增长还是衰变。

播放段落

First, graph the function.

::首先,绘制函数图。

播放段落

Next, answer the question.
::下一个,回答问题。

播放段落

From the graph, the function $\begin{array}{r}y=5^x\end{array}$  represents exponential growth.
::从图中,函数 y=5x 表示指数增长。

播放段落

Review
::回顾

播放段落

Graph each function. Then say whether it represents economic growth or decay.
::每个函数图。 然后说明它是代表经济增长还是代表衰退。

播放段落
1. $\begin{array}{r}y=4^x\end{array}$
   ::y=4x y=4x
播放段落
2. $\begin{array}{r}y={\left(\frac{1}{2}\right)}^x\end{array}$
   ::y=( 12) x
播放段落
3. $\begin{array}{r}y={\left(\frac{1}{3}\right)}^x\end{array}$
   ::y=( 13) x
播放段落
4. $\begin{array}{r}y=7^x\end{array}$
   ::y=7x y=7x
播放段落
5. $\begin{array}{r}y=5^x\end{array}$
   ::y=5x y=5x
播放段落
6. $\begin{array}{r}y=2^x\end{array}$
   ::y=2x y=2x
播放段落
7. $\begin{array}{r}y={\left(\frac{1}{4}\right)}^x\end{array}$
   ::y=( 14) x
播放段落
8. $\begin{array}{r}y={\left(\frac{3}{4}\right)}^x\end{array}$
   ::y=( 34)x
播放段落
9. $\begin{array}{r}y=6^x\end{array}$
   ::y=6x y=6x
播放段落
10. $\begin{array}{r}y={11}^x\end{array}$
    ::y=11x y=11x
播放段落
11. $\begin{array}{r}y=9^x\end{array}$
    ::y=9x y=9x
播放段落
12. $\begin{array}{r}y={\left(\frac{1}{8}\right)}^x\end{array}$
    ::y=( 18) x
播放段落
13.   $\begin{array}{r}y={12}^x\end{array}$
    ::y=12x y=12x
播放段落
14. $\begin{array}{r}y={\left(\frac{2}{5}\right)}^x\end{array}$
    ::y=( 25) x
播放段落
15. $\begin{array}{r}y={13}^x\end{array}$
    ::y=13x y=13x

播放段落

Review (Answers)
::回顾(答复)

播放段落

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。