Section: 查找斜坡- 截取窗体中线条的公式 | 2.2 在斜坡-截取表中查找线的等量

Section outline

You decide to buy a laptop for $800. In 3 years, the laptop will be worth $450. How much will the computer be worth after 6 years?
::你决定用800美元买一台笔记本电脑。三年后,笔记本电脑将值450美元。六年后电脑值多少钱?

Writing a linear equation that relates the two prices will help you determine how much the computer will be worth after 6 years.
::写出一个线性方程,与两种价格相关,将有助于确定6年后计算机的价值。

Finding the Equation of a Line
::查找线条的公式

You know how to find the between two points. We will now find the entire equation of a line. Recall from Algebra I that the equation of a line in slope-intercept form is $\begin{aligned} y = m x + b, \end{aligned}$ where $\begin{aligned} m \end{aligned}$ is the slope and $\begin{aligned} b \end{aligned}$ is the $\begin{aligned} y - \end{aligned}$ intercept . You can find the slope either by using slope triangles or the Slope Formula . To find the $\begin{aligned} y - \end{aligned}$ intercept, or $\begin{aligned} b, \end{aligned}$ you can either locate where the line crosses the $\begin{aligned} y - \end{aligned}$ axis (if given the graph) or by using algebra.
::您知道如何找到两个点之间的方程。我们现在将找到一条线的整个方程。从代数 I 中提醒注意, 斜度截取形式的线的方程是 y=mx+b, 其中 m 是斜度, b 是 y- interphy。您可以使用斜度三角形或斜度公式找到斜度。要找到 y- interception, 或 b, 您可以找到横线横过 y- 轴( 如果给出图形) 的位置, 或者使用代数。

Let's find the equation for the following lines.
::让我们为下面的行寻找方程。

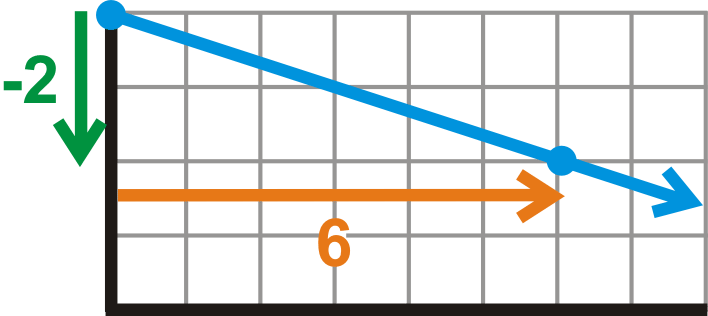
Find the equation of the line below.
::查找下方线的方程式。

Analyze the line. We are given two points on the line, one of which is the $\begin{aligned} y - \end{aligned}$ intercept. From the graph, it looks like the line passes through the $\begin{aligned} y - \end{aligned}$ axis at (0, 4), making $\begin{aligned} b = 4 \end{aligned}$ . Now, we need to find the slope. You can use slope triangles or the Slope Formula. Using slope triangles, we have:
::分析线条。我们得到线条上的两个点, 其中之一是 y - intercut 。从图表看, 线条似乎是通过 y - 轴的( 0, 4 ) , 生成 b= 4 。现在我们需要找到斜坡。您可以使用斜度三角形或斜度公式。使用斜度三角形, 我们可以看到 :

From this, we see that the slope is $\begin{aligned} - \frac{2}{6} \end{aligned}$ or $\begin{aligned} - \frac{1}{3} \end{aligned}$ .
::从这里可以看出,斜坡是-26或-13。

Plugging our found information into the slope-intercept equation, the equation of this line is $\begin{aligned} y = - \frac{1}{3} x + 4 \end{aligned}$ .
::将我们发现的信息插入斜坡界面方程式这条线的方程式是 y13x+4。

Alternate Method : If we had used the Slope Formula, we would use (0, 4) and (6, 2), which are the values of the given points.
::替代方法:如果我们使用了斜坡公式,我们就会使用(0、4和6、2),这是给定点的值。

$\begin{aligned} m = \frac{2 - 4}{6 - 0} = \frac{- 2}{6} = - \frac{1}{3} \end{aligned}$

::m=2-46-02613

The slope of a line is -4 and the $\begin{aligned} y - \end{aligned}$ intercept is (0, 3). What is the equation of the line?
::线的斜坡是 - 4, y - interview 是 (0, 3) 。线的方程是多少 ?

This problem explicitly tells us the slope and $\begin{aligned} y - \end{aligned}$ intercept. The slope is -4, meaning $\begin{aligned} m = - 4 \end{aligned}$ . The $\begin{aligned} y - \end{aligned}$ intercept is (0, 3), meaning $\begin{aligned} b = 3 \end{aligned}$ . Therefore , the equation of the line is $\begin{aligned} y = - 4 x + 3 \end{aligned}$ .
::这个问题清楚地告诉我们斜坡和 y - intercut 。斜坡是 4 , 意思是 m4。 y - intercept 是 (0, 3) , 意思是 b=3 。因此, 线的方程式是 y4x+3 。

The slope of a line is $\begin{aligned} \frac{1}{2} \end{aligned}$ and it passes through the point (4, -7). What is the equation of the line?
::线的斜坡是12, 穿过点( 4, - 7) 。线的方程是多少 ?

In this problem, we are given $\begin{aligned} m \end{aligned}$ and a point on the line. The point, (4, -7) can be substituted in for $\begin{aligned} x \end{aligned}$ and $\begin{aligned} y \end{aligned}$ in the equation. We need to solve for the $\begin{aligned} y - \end{aligned}$ intercept, or $\begin{aligned} b \end{aligned}$ . Plug in what you know to the slope-intercept equation.
::在此问题上, 我们在线上给出 m 和点。点( 4, - 7) 可以替换为 x 和 y 。我们需要解决 y - intercut , 或 b. 插入您所知道的斜坡- intercut 等式。

$\begin{aligned} y & = m x + b \\ - 7 & = \frac{1}{2} (4) + b \\ - 7 & = 2 + b \\ - 9 & = b \end{aligned}$

::y=mx+b-7=12(4)+b-7=2+b-9=b

From this, the equation of the line is $\begin{aligned} y = \frac{1}{2} x - 9 \end{aligned}$ .
::从这里,线条的方程式是 Y=12x- 9 。

We can test if a point is on a line or not by plugging it into the equation. If the equation holds true, the point is on the line. If not, then the point is not on the line.
::我们可以测试一个点是否在线上, 是否在公式中插入。如果公式是真实的, 则点在线上。否则, 点就不会在线上。

Find the equation of the line that passes through (12, 7) and (10, -1).
::查找通过(12、7)和(10、-1)的线条的方程。

In this problem , we are not given the slope or the $\begin{aligned} y - \end{aligned}$ intercept. First, we need to find the slope using the Slope Formula.
::在此问题上,我们没有获得斜坡或y- interview。首先,我们需要使用“ 斜坡公式” 找到斜坡。

$\begin{aligned} m = \frac{- 1 - 7}{10 - 12} = \frac{- 8}{- 2} = 4 \end{aligned}$

::1 - 710 - 128 - 2=4

Now, plug in one of the points for $\begin{aligned} x \end{aligned}$ and $\begin{aligned} y \end{aligned}$ . It does not matter which point you choose because they are both on the line.
::现在,插入 x 和 y 的一个点。您选择哪个点并不重要, 因为它们都在线上。

$\begin{aligned} 7 & = 4 (12) + b \\ 7 & = 48 + b \\ - 41 & = b \end{aligned}$

::7=4(12)+B7=48+b-41=b

The equation of the line is $\begin{aligned} y = 4 x - 41 \end{aligned}$ .
::线的方程式是y=4x-41。

Examples
::实例

Example 1
::例1

Earlier, you were asked to find how much the computer will be worth after 6 years.
::早些时候,有人要求你找出 6年后电脑的价值。

To determine the equation of the line, rewrite the given information as points. The first could be (0, 800) and the second would be (3, 450). We already know that the y -intercept is 800 because the x -value is zero at that point. Find the slope.
::为了确定线条的方程, 请将给定信息重写为点。第一个可能是( 0, 800), 第二个可能是( 3, 450) 。我们已经知道 y 拦截是800 , 因为 X 值在那个点是零。找到斜坡。

$\begin{aligned} \frac{800 - 450}{0 - 3} = - \frac{350}{3} \end{aligned}$

Therefore, the equation of the declining value of the laptop is $\begin{aligned} y = - \frac{350}{3} x + 800 \end{aligned}$ . In 6 years, the laptop will be worth $\begin{aligned} y = - \frac{350}{3} \cdot 6 + 800 = - 700 + 800 = 100 \end{aligned}$ . The laptop will be worth $100.
::因此,膝上型计算机价值下降的方程式是 y3503x+800。 6年后, 膝上型计算机的价值将是 y3503x6+800700+800=100。膝上型计算机的价值将是 100 美元。

Example 2
::例2

What is the equation of the line where the slope is 1 and passes through (5, 3)?
::斜坡为1并经过(5,3)的线的方程是多少?

We are told that $\begin{aligned} m = 1, x = 5, \end{aligned}$ and $\begin{aligned} y = 3 \end{aligned}$ . Plug this into the slope-intercept equation and solve for $\begin{aligned} b \end{aligned}$ .
::我们被告知 m=1,x=5,y=3. 将其插入斜坡截面方程式并解决 b。

$\begin{aligned} 3 & = 1 (5) + b \\ 3 & = 5 + b \\ - 2 & = b \end{aligned}$

::3=1(5)+b3=5+b-2=b

The equation of the line is $\begin{aligned} y = x - 2 \end{aligned}$
::线的方程式是 y=x-2

Example 3
::例3

Find the equation of the line that passes through (9, -4) and (-1, -8).
::查找通过线(9,4)和(1,8)的方程。

First, find the slope.
::首先,找到斜坡

$\begin{aligned} m = \frac{- 8 - (- 4)}{- 1 - 9} = \frac{- 4}{- 10} = \frac{2}{5} \end{aligned}$

::m8-(- 4)- 1- 9 4- 10= 25

Now, find the $\begin{aligned} y - \end{aligned}$ intercept. We will use the second point. Remember, it does not matter which point you use.
::现在,找到y- intermissution。我们将使用第二点。记住, 您使用哪个点并不重要。

$\begin{aligned} - 8 & = \frac{2}{5} (- 1) + b \\ - 8 & = - \frac{2}{5} + b \\ - 7 \frac{3}{5} & = b \end{aligned}$

::-8=25(-1)+b-8=8=25+b-735=b

The equation of the line is $\begin{aligned} y = \frac{2}{5} x - 7 \frac{3}{5} \end{aligned}$ or $\begin{aligned} y = \frac{2}{5} x - \frac{38}{5} \end{aligned}$ .
::线的方程式是y=25x-735或y=25x-385。

When your $\begin{aligned} y - \end{aligned}$ intercept is a fraction , make sure it is reduced. Double-check with your teacher on how s/he wants you to leave your answer.
::当y- interclution是分数时, 请确定它会缩小。请与您的老师进行双倍检查, 以确定您希望您如何不回答问题。

Example 4
::例4

Find the equation of the line below.
::查找下方线的方程式。

We can find the slope one of two ways: using slope triangles or by using the Slope Formula. We are given (by the drawn points in the picture) that (-2, 2) and (4, -2) are on the line. Drawing a slope triangle, we have:
::我们可以找到斜坡的两种方式之一:使用斜坡三角形或使用斜坡公式。我们(根据图中绘制的点)被给出了(2、2和4、2)在线上。我们绘制了斜坡三角形:

We have that the slope is $\begin{aligned} - \frac{4}{6} \end{aligned}$ or $\begin{aligned} - \frac{2}{3} \end{aligned}$ . To find the $\begin{aligned} y - \end{aligned}$ intercept, it looks like it is somewhere between 0 and 1. Take one of the points and plug in what you know to the slope-intercept equation.
::我们发现斜坡是-46 或- 23。要找到 y - interview, 它看起来像它在 0 和 1 之间。选择一个点并插入您知道的斜坡 intercept 等式。

$\begin{aligned} 2 & = - \frac{2}{3} (- 2) + b \\ 2 & = \frac{4}{3} + b \\ \frac{2}{3} & = b \end{aligned}$

::*=============================================================================================================================================================================================================================================================================================================================================================================================================================================================================================================================

The equation of the line is $\begin{aligned} y = - \frac{2}{3} x + \frac{2}{3} \end{aligned}$ .
::线的方程式是 y23x+23。

Review
::回顾

Find the equation of each line with the given information below.
::以下文提供的信息查找每行的方程。

slope = 2, $\begin{aligned} y - \end{aligned}$ intercept = (0, 3)
::斜坡 = 2, y- 界面 = (0, 3)

$\begin{aligned} m = - \frac{1}{4}, b = 2.6 \end{aligned}$
::m14, b=2.6

slope = -1, $\begin{aligned} y - \end{aligned}$ intercept = (0, 2)
::斜坡 = -1, y - 界面 = (0, 2)

$\begin{aligned} x - \end{aligned}$ intercept = (-2, 0), $\begin{aligned} y - \end{aligned}$ intercept = (0, -5)
::x- 截取 = (-2, 0, y- 截取 = (0, 5)

slope $\begin{aligned} = \frac{2}{3} \end{aligned}$ and passes through (6, -4)
::斜坡=23,通过(6,4)

slope $\begin{aligned} = - \frac{3}{4} \end{aligned}$ and passes through (-2, 5)
::斜度 34 并通过 (-2, 5)

slope = -3 and passes through (-1, -7)
::斜坡 = - 3 和通过 (-1 - 7)

slope = 1 and passes through (2, 4)
::斜坡=1,通过(2,4)

passes through (-5, 4) and (1, 1)
::通过(5、4和1、1和1)

passes through (5, -1) and (-10, -10)
::通过(5,-1)和(10,-10)

passes through (-3, 8) and (6, 5)
::通过(-3,8)和(6,5)

passes through (-4, -21) and (2, 9)
::通过(4-4-21)和(2,9)

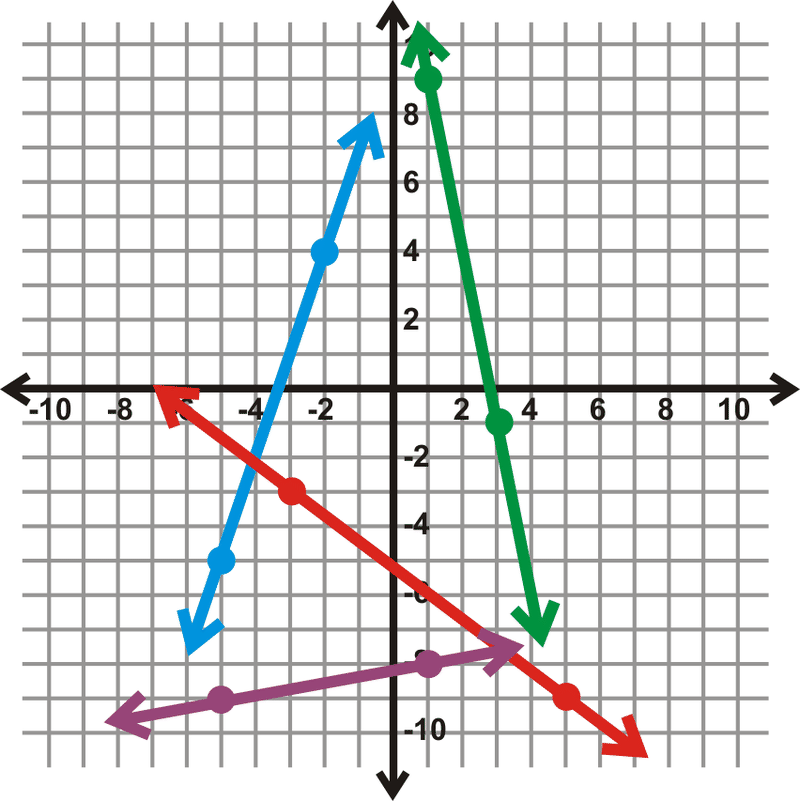
For problems 13-16, find the equation of the lines in the graph below.
::对于问题13-16,请在下图中找到行的方程式。

Green Line
::绿线

Blue Line
::" 蓝线 " 蓝线

Red Line
::红线

Purple Line
::紫线

Find the equation of the line with zero slope and passes through (8, -3).
::查找线条的方程式为零斜度,通过(8, - 3)。

Find the equation of the line with zero slope and passes through the point (-4, 5).
::查找线的方程式为零斜度,通过点(-4、5)。

Find the equation of the line with zero slope and passes through the point $\begin{aligned} (a, b) \end{aligned}$ .
::查找线条的方程式为零斜度,通过点(a,b)。

Challenge Find the equation of the line with an undefined slope that passes through $\begin{aligned} (a, b) \end{aligned}$ .
::" 挑战 " :寻找线的方程式,用一个未定义的斜坡通过(a,b)。

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

Section outline

Finding the Equation of a Line ::查找线条的公式

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

Review ::回顾

Review (Answers) ::回顾(答复)

Finding the Equation of a Line
::查找线条的公式

Examples
::实例

Example 1
::例1

Example 2
::例2

Example 3
::例3

Example 4
::例4

Review
::回顾

Review (Answers)
::回顾(答复)