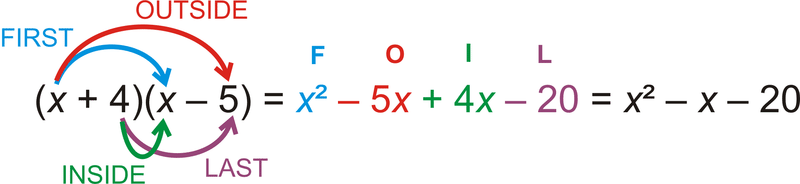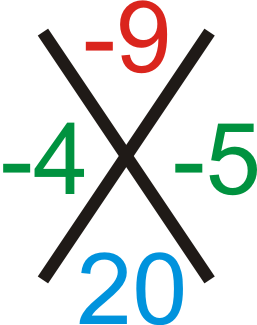Section: 当领导系数等于1时的乘数 | 5.1 主导系数值等于1时的保理

Section outline

The area of a rectangle is $\begin{aligned} x^{2} - 3 x - 28 \end{aligned}$ . What are the length and width of the rectangle?
::矩形区域为 x2-3x-28。矩形的长度和宽度是多少?

Factoring a Quadratic Equation
::计算赤道等量的乘数

A quadratic equation has the form $\begin{aligned} a x^{2} + b x + c \end{aligned}$ , where $\begin{aligned} a \neq 0 \end{aligned}$ (If $\begin{aligned} a = 0 \end{aligned}$ , then the equation would be linear). For all quadratic equations, the 2 is the largest and only exponent . A quadratic equation can also be called a trinomial when all three terms are present.
::二次方程的窗体为 ax2+bx+c, 其中 a0 (如果 a=0, 则方程为线性)。对于所有二次方程, 2 是最大且唯一的引号。当所有三个条件都存在时, 二次方程也可以称为三角方程。

There are four ways to solve a quadratic equation. The easiest is factoring . In this concept, we are going to focus on factoring when $\begin{aligned} a = 1 \end{aligned}$ or when there is no number in front of $\begin{aligned} x^{2} \end{aligned}$ .
::有四种方法可以解析二次方程。最容易的方法是乘数。在这个概念中, 我们将集中关注当 =1 或 x2 前面没有数字时的乘数。

To review the process of multiplying two factors together, let's multiply $\begin{aligned} (x + 4) (x - 5) \end{aligned}$ .
::为了审查将两个因素乘以一起的过程,让我们来审查乘以(x+4)(x-5)的过程。

Even though this is not a quadratic, the product of the two factors will be. Remember from previous math classes that a factor is a number that goes evenly into a larger number. For example, 4 and 5 are factors of 20. So, to determine the larger number that $\begin{aligned} (x + 4) \end{aligned}$ and $\begin{aligned} (x - 5) \end{aligned}$ go into, we need to multiply them together. One method for multiplying two polynomial factors together is called FOIL. To do this, you need to multiply the FIRST terms, OUTSIDE terms, INSIDE terms, and the LAST terms together and then combine like terms .
::虽然这不是一个二次曲线, 但这两个因素的产物是两个因素的产物。请记住, 从以前的数学等级中, 一个系数是一个偶数, 偶数进入一个较大的数字。例如, 4和5是20。因此, 要确定进进( x+4) 和 ( x-5) 的较大数字, 我们需要把它们相乘。将两个多元因素相乘的一个方法叫做 FIL。要做到这一点, 您需要将第一个术语、外源术语、 INSIDE 术语和 LAST 术语合并, 然后将类似术语合并。

Therefore $\begin{aligned} (x + 4) (x - 5) = x^{2} - x - 20 \end{aligned}$ . We can also say that $\begin{aligned} (x + 4) \end{aligned}$ and $\begin{aligned} (x - 5) \end{aligned}$ are factors of $\begin{aligned} x^{2} - x - 20 \end{aligned}$ .
::因此(x+4)(x-5)=x2-x-20,我们也可以说(x+4)和(x-5)是x2-x-20的因素。

Now, we will “undo” the multiplication of two factors by factoring. In this concept, we will only address quadratic equations in the form $\begin{aligned} x^{2} + b x + c \end{aligned}$ , or when $\begin{aligned} a = 1 \end{aligned}$ .
::现在,我们将“不做”两个因子乘法的乘法。在这个概念中,我们将只处理 x2+bx+c 形式的二次方程,或者当 a=1 时。

Factoring
::保理

Step 1: From the previous problem , we know that $\begin{aligned} (x + m) (x + n) = x^{2} + b x + c \end{aligned}$ .
::第1步:从上一个问题中,我们知道(x+m)(x+n)=x2+bx+c。

FOIL $\begin{aligned} (x + m) (x + n) \end{aligned}$ .
::FOIL(x+m)(x+n) (x+m)(x+n)。

$\begin{aligned} (x + m) (x + n) \Rightarrow x^{2} + \underset{b x}{\underset{⏟}{n x + m x}} + \underset{c}{\underset{⏟}{m n}} \end{aligned}$

:x+m)(x+n) x2+nx+mx__bx+mn}c

Step 2: This shows us that the constant term , or $\begin{aligned} c \end{aligned}$ , is equal to the product of the constant numbers inside each factor. It also shows us that the coefficient in front of $\begin{aligned} x \end{aligned}$ , or $\begin{aligned} b \end{aligned}$ , is equal to the sum of these numbers.
::第2步:这向我们表明,恒定值或 c 等于每个系数内恒定数的产物。它也向我们表明, x 或 b 前的系数等于这些数字的总和。

Step 3: Group together the first two terms and the last two terms. Find the Greatest Common Factor , or GCF, for each pair.
::第3步:将前两个任期和最后两个任期组合起来,为每对夫妇找出最伟大的共同因素,即绿色气候基金。

$\begin{aligned} (x^{2} + n x) + (m x + m n) \\ x (x + n) + m (x + n) \end{aligned}$

:x2+nx)+(mx+mn)x(x+n)+m(x+n)

Step 4: Notice that what is inside both sets of parenthesis in Step 3 is the same. This number, $\begin{aligned} (x + n) \end{aligned}$ , is the GCF of $\begin{aligned} x (x + n) \end{aligned}$ and $\begin{aligned} m (x + n) \end{aligned}$ . You can pull it out in front of the two terms and leave the $\begin{aligned} x + m \end{aligned}$ .
::第4步:请注意,第3步中两组括号内的内容相同。这个数字(x+n)是 x(x+n) 和 m(x+n) 的绿色气候基金。你可以在这两个条件之前把它拉出来,离开 x+m。

$\begin{aligned} x (x + n) + m (x + n) \\ (x + n) (x + m) \end{aligned}$

:xx+n)+m(x+n)(x+n)(x+n)(x+m)

We have now shown how to go from FOIL-ing to factoring and back.
::我们现在已经展示了如何从FOILing到保理和返回。

Let’s apply this idea to a practice problem and factor $\begin{aligned} x^{2} + 6 x + 8 \end{aligned}$ .
::让我们把这个想法应用于实践问题和因子 x2+6x+8。

Use the steps above for help.
::使用上述步骤帮助。

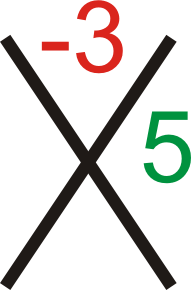
$\begin{aligned} x^{2} + 6 x + 8 = (x + m) (x + n) \end{aligned}$

::x2+6x+8=(x+m)(x+n)

So, from Step 2, $\begin{aligned} b \end{aligned}$ will be equal to the sum of $\begin{aligned} m \end{aligned}$ and $\begin{aligned} n \end{aligned}$ and $\begin{aligned} c \end{aligned}$ will be equal to their product. Applying this to our problem, $\begin{aligned} 6 = m + n \end{aligned}$ and $\begin{aligned} 8 = m n \end{aligned}$ . To organize this, use an “ $\begin{aligned} X \end{aligned}$ ”. Place the sum in the top and the product in the bottom.
::因此,从步骤2, b 将等于 m 和 n 和 c 的总和, c 将等于他们的产品。将此应用到我们的问题中, 6 = m+n 和 8 = mn。要组织它, 请使用“ X ” 。将总和放在顶部, 产品放在底部。

The green pair above is the only one that also adds up to 6. Now, move on to Step 3. We need to rewrite the $\begin{aligned} x - \end{aligned}$ term, or $\begin{aligned} b \end{aligned}$ , as a sum of $\begin{aligned} m \end{aligned}$ and $\begin{aligned} n \end{aligned}$ .
::上面的绿色对子是唯一一个加到6的对子,现在,继续到第3步,我们需要重写x-sterm,或b,作为m和n的总和。

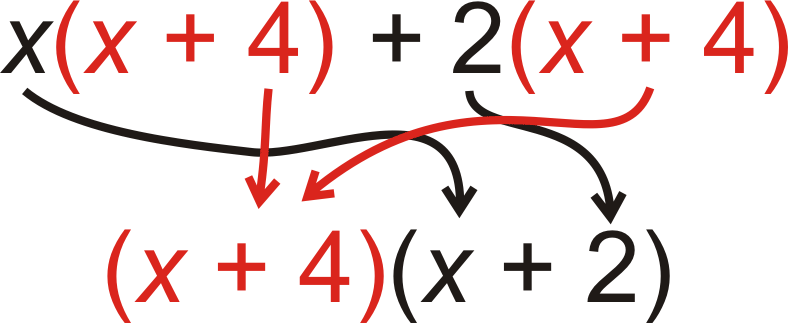
$\begin{aligned} x^{2} + 6 x + 8 \\ ↙ ↘ \\ x^{2} + 4 x + 2 x + 8 \\ (x^{2} + 4 x) + (2 x + 8) \\ x (x + 4) + 2 (x + 4) \end{aligned}$

::x2+6x+82+4x+2x8(x2+4x)+(2x+8)x(x+4)+2(x+4)+2(x+4)

Moving on to Step 4, we notice that the $\begin{aligned} (x + 4) \end{aligned}$ term is the same. Pull this out and we are done.
::继续到第四步,我们注意到(x+4)一词是一样的。拉出来,我们就完了。

Therefore, the factors of $\begin{aligned} x^{2} + 6 x + 8 \end{aligned}$ are $\begin{aligned} (x + 4) (x + 2) \end{aligned}$ . You can FOIL this to check your answer.
::因此, x2+6x+8 的因数是 (x+4)(x+2) 。您可以通过 FIL 来查看您的答案。

Let's factor $\begin{aligned} x^{2} + 12 x - 28 \end{aligned}$ .
::以乘数 x2+12x- 28 表示。

We can approach this problem in exactly the same way we did in the previous problem . This time, we will not use the “ $\begin{aligned} X \end{aligned}$ .” What are the factors of -28 that also add up to 12? Let’s list them out to see:
::我们可以以与前一个问题完全相同的方式来处理这个问题。这次,我们不会使用“X ” ( X ) 。 28 中哪些因素加起来也等于12? 让我们列举一下:

$\begin{aligned} - 4 \cdot 7, 4 \cdot - 7, 2 \cdot - 14, - 2 \cdot 14, 1 \cdot - 28, - 1 \cdot 28 \end{aligned}$

The $\begin{aligned} r e d \end{aligned}$ pair above is the one that works. Notice that we only listed the factors of negative 28.
::上面的红对是有效的。注意我们只列出了负28的因素。

$\begin{aligned} x^{2} + 12 x - 28 \\ ↙ ↘ \\ x^{2} - 2 x + 14 x - 28 \\ (x^{2} - 2 x) + (14 x - 28) \\ x (x - 2) + 14 (x - 2) \\ (x - 2) (x + 14) \end{aligned}$

::x2+12x--2-28 x2-2-2x+14x-28(x2-2x)+(14x-2x)+(14x-2)x(x-2)+14(x-2)(x-2)(x-2)(x+14)

A couple of notes:
::几个注解:

Does it matter which $\begin{aligned} x - \end{aligned}$ term you put first? No, order does not matter. In the previous problem , we could have put $\begin{aligned} 14 x \end{aligned}$ followed by $\begin{aligned} - 2 x \end{aligned}$ . We would still end up with the same answer.
::您先放哪个x- 期是否重要? 不 , 顺序并不重要。在前一个问题中, 我们可以先放14x, 然后再放- 2x。我们最后还是会有相同的答案。

Can I skip the “expanded” part (Steps 3 and 4 above )? Yes and No. Yes, if $\begin{aligned} a = 1 \end{aligned}$ . If $\begin{aligned} a = 1 \end{aligned}$ , then $\begin{aligned} x^{2} + b x + c = (x + m) (x + n) \end{aligned}$ such that $\begin{aligned} m + n = b \end{aligned}$ and $\begin{aligned} m n = c \end{aligned}$ . Consider this a shortcut. No, if $\begin{aligned} a \neq 1 \end{aligned}$ .
::我可以跳过“扩展”部分( 上面的步骤 3 和 4) 吗 ? 是和否。如果 a= 1. Ifa= 1, 后x2+bx+c=( x+m ( x+n) , 则m+n=bandmn=c。请将此视为捷径。如果 a+1 , 则是否。

Let's factor $\begin{aligned} x^{2} - 4 x \end{aligned}$ .
::让我们用乘数 x2 - 4x。

This is an example of a quadratic that is not a trinomial because it only has two terms, also called a binomial . There is no $\begin{aligned} c \end{aligned}$ , or constant term. To factor this, we need to look for the GCF. In this case, the largest number that can be taken out of both terms is an $\begin{aligned} x \end{aligned}$ .
::这是一个不是三进制的四进制的例子,因为它只有两个术语, 也称为二进制。没有 c 或常数。为了考虑到这一点, 我们需要寻找绿色气候基金。在这个例子中, 两个术语中最大的数字是 x。

$\begin{aligned} x^{2} - 4 x = x (x - 4) \end{aligned}$

::x2 - 4x=x(x- 4)

Therefore, the factors are $\begin{aligned} x \end{aligned}$ and $\begin{aligned} x - 4 \end{aligned}$ .
::因此,因素是x和x-4。

Examples
::实例

Example 1
::例1

Earlier, you were asked to find the length and width of the rectangle.
::早些时候,有人要求你找到矩形的长度和宽度。

Recall that the area of a rectangle is $\begin{aligned} A = l w \end{aligned}$ , where l is the length and w is the width. To find the length and width, we can therefore factor the area $\begin{aligned} x^{2} - 3 x - 28 \end{aligned}$ .
::回想一个矩形的区域是 A=lw, 其中 I 是长度, w 是宽度。要找到长度和宽度, 我们可以因此将区域乘以 x2 - 3x - 28 。

What are the factors of –28 that add up to –3? Testing the various possibilities, we find that $\begin{aligned} - 7 \cdot 4 = - 28 \end{aligned}$ and $\begin{aligned} - 7 + 4 = - 3 \end{aligned}$ .
::28和3之间的因素是什么?测试各种可能性,我们发现7+428和7+4+3。

Therefore, $\begin{aligned} x^{2} - 3 x - 28 \end{aligned}$ factors to $\begin{aligned} (x - 7) (x + 4) \end{aligned}$ , and one of these factors is the rectangle's length while the other is its width.
::因此,x2-3x-28乘以(x-7)(x+4),其中一个因素是矩形的长度,另一个因素是其宽度。

Example 2
::例2

Multiply $\begin{aligned} (x - 3) (x + 8) \end{aligned}$ .
::乘(x-3)(x+8)。

FOIL-ing our factors together, we get:
::结合我们的因素,我们得到:

$\begin{aligned} (x - 3) (x + 8) = x^{2} + 8 x - 3 x - 24 = x^{2} + 5 x - 24 \end{aligned}$

:x-3(x+8)=x2+8x-3x-3x-24=x2+5x-24)

Factor the following quadratics, if possible.
::如果可能,则以下列二次方位因子为因数。

Example 3
::例3

$\begin{aligned} x^{2} - 9 x + 20 \end{aligned}$
::x2-9x+20 x2 - 9x+20

Using the “ $\begin{aligned} X \end{aligned}$ ,” we have:
::使用“X”,我们有:

From the shortcut above, $\begin{aligned} - 4 + - 5 = - 9 \end{aligned}$ and $\begin{aligned} - 4 \cdot - 5 = 20 \end{aligned}$ .
::从上面的捷径, - 459 和 - 45=20。

$\begin{aligned} x^{2} - 9 x + 20 = (x - 4) (x - 5) \end{aligned}$

::x2-9x+20=(x-4)(x-5)

Example 4
::例4

$\begin{aligned} x^{2} + 7 x - 30 \end{aligned}$
::x2+7x-30

Let’s list out all the factors of -30 and their sums. The sums are in red.
::让我们列出 - 30 及其金额的所有因素。数字是红色的。

$\begin{aligned} - 10 \cdot 3 (- 7), - 3 \cdot 10 (7), - 2 \cdot 15 (13), - 15 \cdot 2 (- 13), - 1 \cdot 30 (29), - 30 \cdot 1 (- 29) \end{aligned}$

From this, the factors of -30 that add up to 7 are -3 and 10. $\begin{aligned} x^{2} + 7 x - 30 = (x - 3) (x + 10) \end{aligned}$
::由此,乘以-30乘以7的系数为-3和10 x2+7x-30=(x-3)(x+10)

Example 5
::例5

$\begin{aligned} x^{2} + x + 6 \end{aligned}$
::x2+x+6 x2+6

There are no factors of 6 that add up to 1. If we had -6, then the trinomial would be factorable. But, as is, this is not a factorable trinomial.
::没有6个因素加起来等于1。如果我们加到 - 6, 那么三角是可以考虑的因素。但是,和现在一样,这不是一个可以考虑的三重因素。

Example 6
::例6

$\begin{aligned} x^{2} + 10 x \end{aligned}$
::x2+10xx

The only thing we can do here is to take out the GCF. $\begin{aligned} x^{2} + 10 x = x (x + 10) \end{aligned}$
::我们唯一能做的就是除掉全球合作框架。 x2+10x=xx(x+10)

Review
::回顾

Multiply the following factors together.
::将下列因素合并乘以。

$\begin{aligned} (x + 2) (x - 8) \end{aligned}$
:x+2)(x-8)

$\begin{aligned} (x - 9) (x - 1) \end{aligned}$
:x-9)(x-1)

$\begin{aligned} (x + 7) (x + 3) \end{aligned}$
:x+7(x+3))

Factor the following quadratic equations. If it cannot be factored, write not factorable . You can use either method presented in the examples.
::\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \

$\begin{aligned} x^{2} - x - 2 \end{aligned}$
::x2 - x-2

$\begin{aligned} x^{2} + 2 x - 24 \end{aligned}$
::x2+2x- 24

$\begin{aligned} x^{2} - 6 x \end{aligned}$
::x2 - 6x

$\begin{aligned} x^{2} + 6 x + 9 \end{aligned}$
::x2+6x+9

$\begin{aligned} x^{2} + 8 x - 10 \end{aligned}$
::x2+8x- 10

$\begin{aligned} x^{2} - 11 x + 30 \end{aligned}$
::x2 - 11x+30

$\begin{aligned} x^{2} + 13 x - 30 \end{aligned}$
::x2+13x-30

$\begin{aligned} x^{2} + 11 x + 28 \end{aligned}$
::x2+11x+28 x2+11x+28

$\begin{aligned} x^{2} - 8 x + 12 \end{aligned}$
::x2-8x+12 x2-8x+12

$\begin{aligned} x^{2} - 7 x - 44 \end{aligned}$
::x2 - 7x-44

$\begin{aligned} x^{2} - 8 x - 20 \end{aligned}$
::x2 - 8x - 20

$\begin{aligned} x^{2} + 4 x + 3 \end{aligned}$
::x2+4x+3 x2+4x+3

$\begin{aligned} x^{2} - 5 x + 36 \end{aligned}$
::x2 - 5x+36

$\begin{aligned} x^{2} - 5 x - 36 \end{aligned}$
::x2 - 5x-36

$\begin{aligned} x^{2} + x \end{aligned}$
::x2+xxx x2+xx

Challenge Fill in the $\begin{aligned} X \end{aligned}$ ’s below with the correct numbers.
::以正确的数字填充X的以下数字。

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

Section outline

Factoring a Quadratic Equation ::计算赤道等量的乘数

Factoring ::保理

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

Example 5 ::例5

Example 6 ::例6

Review ::回顾

Review (Answers) ::回顾(答复)

Factoring a Quadratic Equation
::计算赤道等量的乘数

Factoring
::保理

Examples
::实例

Example 1
::例1

Example 2
::例2

Example 3
::例3

Example 4
::例4

Example 5
::例5

Example 6
::例6

Review
::回顾

Review (Answers)
::回顾(答复)