立方体总和和差数

播放段落

The volume of a rectangular prism is $\begin{align*}2x^4 - 128x\end{align*}$ . What are the lengths of the prism's sides?
::矩形棱柱体积为 2x4 - 128x。 棱柱面的长度是多少?

播放段落

Sum and Difference of Cubes
::立方体总和和差数

播放段落

Previously, you learned how to factor several different types of quadratic equations. Here, we will expand this knowledge to certain types of . The first is the sum of cubes. The sum of cubes is what it sounds like, the sum of two cube numbers or $\begin{align*}a^3+b^3\end{align*}$ . We will investi gate  volume to find the factorization of this polynomial . 
::之前, 您学会了如何将几种不同的二次方程乘以 。 在这里, 我们将将这种知识扩展至某些类型的 。 第一个是立方体的总和。 立方体的总和是它听起来像的, 两个立方体数字或 a3+b3 的和。 我们将调查音量, 以找到这个多面体的乘数 。

播放段落

Sum of Cubes Formula
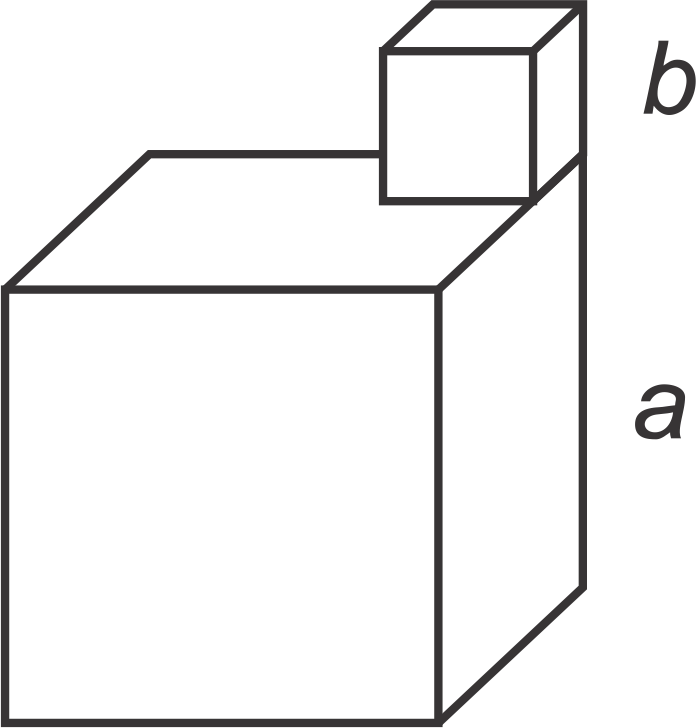
::立方公式总和

播放段落

Step 1: Pictorially, the sum of cubes looks like this:
::第1步: 片段: 立方体的总和是这样的:

播放段落

Or, we can put one on top of the other.
::或者,我们可以把一个放在另一个上面。

播放段落

Step 2: Recall that the formula for volume is $\begin{align*}length \times width \times depth\end{align*}$ . Find the volume of the sum of these two cubes.
::步骤 2: 提醒注意体积的公式是长度xwidthx深度。 查找这两个立方体的总和的体积 。

播放段落

$\begin{align*}V = a^3+b^3\end{align*}$
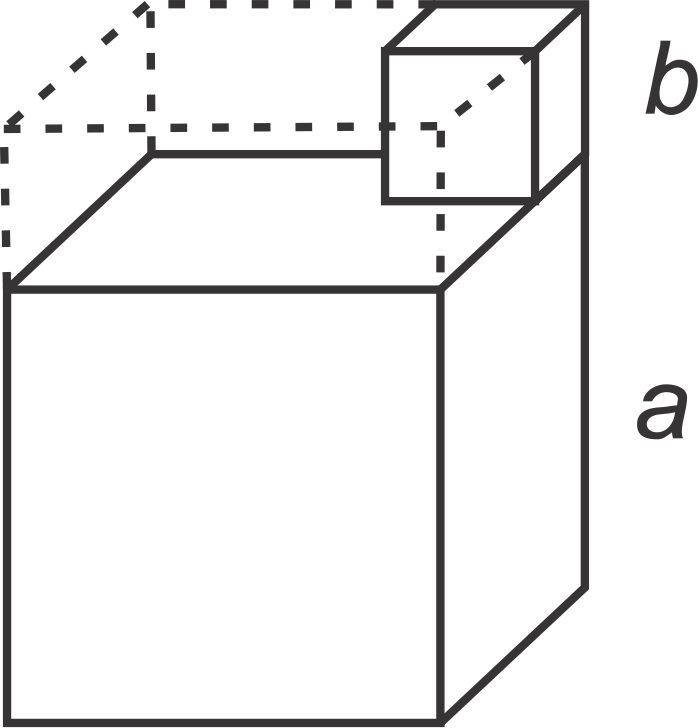
::V=a3+b3 =a3+b3 =a3+b3

播放段落

Step 3: Now, we will find the volume in a different way. Using the second picture above, we will add in imaginary lines so that these two cubes look like one large prism. Find the volume of this prism.
::步骤 3 : 现在, 我们将以不同的方式找到音量 。 使用上面的第二幅图片, 我们将添加想象中的线条, 这样这两个立方体看起来像一个大棱镜。 找到这个棱镜的音量 。

播放段落

$$\begin{align*}V &= a \times a \times(a+b)\\ &= a^2(a+b)\end{align*}$$
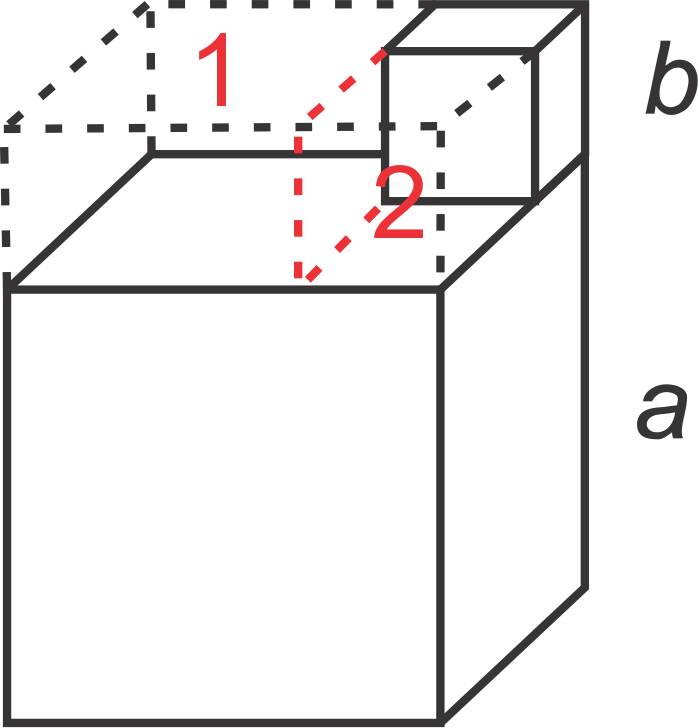
::V=axxaxxx(a+b)=a2(a+b)

播放段落

Step 4: Subtract the imaginary portion on top. In the picture, they are prism 1 and prism 2.
::步骤 4 : 减去上面的假想部分。 在图片中, 它们是棱镜 1 和棱镜 2 。

播放段落

$$\begin{align*}V = a^2(a+b) - \left[\underbrace{ab(a-b)}_{{\color{red}Prism \ 1}} + \underbrace{b^2(a-b)}_{{\color{red}Prism \ 2}}\right]\end{align*}$$
::V=a2(a+b)-[a(a-b)-[a(a-b)-Prism 1+b2(a-b)-Prism 2]

播放段落

Step 5: Pull out any common factors within the brackets .
::步骤5:排除括号内的任何共同因素。

播放段落

$\begin{align*}V = a^2(a+b)-b(a-b)[a+b]\end{align*}$
::V=a2(a+b)-b(a-b)[a+b]

播放段落

Step 6: Notice that both terms have a common factor of $\begin{align*}(a + b)\end{align*}$ . Pull this out, put it in front, and get rid of the brackets.
::步骤6:注意这两个术语有一个共同的(a+b)因素,拉出来,放在前面,去掉括号。

播放段落

$\begin{align*}V = (a+b)(a^2-b(a-b))\end{align*}$
::V=(a+b)(a2-b(a-b))

播放段落

Step 7: Simplify what is inside the second set of parenthesis.
::步骤7:简化第二组括号内的内容。

播放段落

$\begin{align*}V = (a+b)(a^2-ab+b^2)\end{align*}$
::V=(a+b)(a2-ab+b2)

播放段落

In the last step, we found that $\begin{align*}a^3+b^3\end{align*}$ factors to $\begin{align*}(a+b)(a^2-ab+b^2)\end{align*}$ . This is the Sum of Cubes Formula .
::在最后一步,我们发现A3+b3 到(a+b)(a2-ab+b2)。 这是立方体公式总和。

播放段落

Let's factor $\begin{align*}8x^3+27\end{align*}$ .
::让我们来乘以8x3+27。

播放段落

First, determine if these are “cube” numbers. A cube number has a cube root . For example, the cube root of 8 is 2 because $\begin{align*}2^3 = 8\end{align*}$ . $\begin{align*}3^3 = 27, 4^3 = 64, 5^3 = 125\end{align*}$ , and so on.
::首先, 确定这些是否为“ 立方体” 数字。 一个立方体数字有一个立方根。 例如, 8 的立方根为 2, 因为 23= 8, 33= 27, 43= 64, 53=125, 等等 。

播放段落

$$\begin{align*}a^3 &= 8x^3 = (2x)^3 \qquad b^3 = 27 = 3^3\\ a &= 2x \qquad \qquad \qquad \ b = 3\end{align*}$$
::a3=8x3=(2x)3b3=27=33a=2xb=3

播放段落

In the formula, we have:
::在公式中,我们有:

播放段落

$$\begin{align*}(a+b)(a^2-ab+b^2) &= (2x+3)((2x)^2-(2x)(3)+3^2)\\ &= (2x+3)(4x^2-6x+9)\end{align*}$$
:a+b)(a2-ab+b2)=(2x+3)((2x)2-(2x)(3)+32)=(2x+3)(4x2-6x+9)

播放段落

Therefore , $\begin{align*}8x^3+27 = (2x+3)(4x^2-6x+9)\end{align*}$ . The second factored polynomial does not factor any further.
::因此,8x3+27=(2x+3)(4x2-6x+9),第二个乘数多元系数不再考虑。

播放段落

Difference of Cubes
::立方体差异

播放段落

Step 1: Pictorially, the difference of cubes looks like this:
::第1步: 片段: 立方体的差别看起来是这样的:

播放段落

Imagine the smaller cube is taken out of the larger cube.
::想象一下小的立方体是从大的立方体里取出来的

播放段落

Step 2: Recall that the formula for volume is $\begin{align*}length \times width \times depth\end{align*}$ . Find the volume of the difference of these two cubes.
::步骤 2: 提醒注意体积的公式是长度xwidthx深度。 查找这两个立方体的差异大小 。

播放段落

$\begin{align*}V = a^3-b^3\end{align*}$
::V=a3-3-b3 级

播放段落

Step 3: Now, we will find the volume in a different way. Using the picture here, will add in imaginary lines so that the shape is split into three prisms. Find the volume of prism 1, prism 2, and prism 3.
::步骤 3 : 现在, 我们将以不同的方式找到音量 。 使用此图片, 将会添加想象的线条, 这样形状可以分割成三个棱镜 3 。 找到棱镜 1 、 棱镜 2 和棱镜 3 的音量 。

播放段落

$$\begin{align*}& \text{Prism} \ 1: a \cdot a \cdot (a-b)\\ & \text{Prism} \ 2: a \cdot b \cdot (a-b)\\ & \text{Prism} \ 3: b \cdot b \cdot (a-b)\end{align*}$$
::棱晶 1:aa(a-b) 棱 2:ab(a-b) 棱 3:bb(a-b)

播放段落

Step 4: Add the volumes together to get the volume of the entire shape.
::第4步:将卷卷加在一起,以获得整个形状的体积。

播放段落

$\begin{align*}V = a^2(a-b)+ab(a-b)+b^2(a-b)\end{align*}$
::V=a2(a-b)+ab(a-b)+b2(a-b)+b2(a-b)

播放段落

Step 5: Pull out any common factors and simplify.
::步骤5:排除任何共同因素并简化。

播放段落

$\begin{align*}V = (a-b)(a^2+ab+b^2)\end{align*}$
::V=(a-b)(a2+ab+b2)

播放段落

In the last step, we found that $\begin{align*}a^3-b^3\end{align*}$ factors to $\begin{align*}(a-b)(a^2+ab+b^2)\end{align*}$ . This is the Difference of Cubes Formula .
::在最后一步,我们发现A3-b3至(a-b)(a2+ab+b2)的因素是立方体公式的差异。

播放段落

Let's factor $\begin{align*}x^5-125x^2\end{align*}$ .
::以乘数 x5 - 125x2 。

播放段落

First, take out any common factors.
::首先,排除任何共同因素。

播放段落

$$\begin{align*}x^5-125x^2 = x^2(x^3-125)\end{align*}$$
::x5 - 125x2=x2( x3 - 125)

播放段落

What is inside the parenthesis is a difference of cubes. Use the formula.
::括号内的内容是立方体的差别。使用公式。

播放段落

$$\begin{align*}x^5-125x^2 &= x^2(x^3-125)\\ &= x^2(x^3-5^3)\\ &= x^2(x-5)(x^2+5x+25)\end{align*}$$
::x5-225x2=x2(x3-125)=x2(x3-53)=x2(x3-53)=x2(x-5)(x2+5x+25)

播放段落

Now, let's find the real-number solutions of $\begin{align*}x^3-8 = 0\end{align*}$ .
::现在,让我们找到X3 - 8=0的真数字解决方案。

播放段落

Factor using the difference of cubes.
::使用立方体差的系数 。

播放段落

$$\begin{align*}x^3-8 &= 0\\ (x-2)(x^2+2x+4) &= 0\\ x& = 2\end{align*}$$
::x3-8=0(x- 2)(x2+2x+4)=0x=2

播放段落

In the last step, we set the first factor equal to zero. The second factor, $\begin{align*}x^2+2x+4\end{align*}$ , will give imaginary solutions. For both the sum and difference of cubes, this will always happen.
::最后一步,我们将第一个系数设为零。第二个系数 x2+2x+4 将给出假想的解决方案。对于立方体的总和和和差数,这种情况总是会发生。

播放段落

Examples
::实例

播放段落

Example 1
::例1

播放段落

Earlier, you were asked to find  the lengths of the prism's sides.
::早些时候,有人要求你找出棱镜两面的长度。

播放段落

We need to factor $\begin{align*}2x^4 - 128x\end{align*}$ .
::我们需要乘以2x4 -128x。

播放段落

First, take out any common factors.
::首先,排除任何共同因素。

播放段落

$$\begin{align*}2x^4 - 128x = 2x(x^3 - 64)\end{align*}$$
::2x4-128x=2x(x3-64)

播放段落

What is inside the parenthesis is a difference of cubes. Use the Difference of Cubes Formula.
::括号内的内容是立方体的区别。使用立方体公式的差异。

播放段落

$$\begin{align*}2x(x^3 - 64)\\ &= 2x(x^3 - 4^3)\\ &= 2x(x - 4)(x^2 + 4x + 16)\end{align*}$$
::2x(x3-64)=2x(x3-43-43)=2x(x4)(x2+4x+16)

播放段落

Therefore, the side lengths of the rectangular prism are $\begin{align*}2x\end{align*}$ , $\begin{align*}x +4\end{align*}$ , and $\begin{align*}x^2 + 4x + 16\end{align*}$ .
::因此,矩形棱柱的侧长为2x、x+4和x2+4x+16。

播放段落

Example 2
::例2

播放段落

Factor using the difference of cubes: $\begin{align*}x^3−1\end{align*}$
::使用立方体差数的系数: x3- 1

播放段落

$$\begin{align*}x^3-1 &= x^3-1^3\\ &= (x-1)(x^2+x+1)\end{align*}$$
::x3- 1=x3- 13=(x-1)(x2+x+1)

播放段落

Example 3
::例3

播放段落

Factor using the sum or difference of cubes:  $\begin{align*}3x^3+192\end{align*}$
::使用立方体总和或差数的系数: 3x3+192

播放段落

Pull out the 3, then factor using the sum of cubes.
::用立方体的总和拔出3,然后因子。

播放段落

$$\begin{align*}3x^3+192 &= 3(x^3+64)\\ &= 3(x^3+4^3)\\ &= 3(x+4)(x^2-4x+16)\end{align*}$$
::3x3+192=3(x3+64)=3(x3+43)=3(x+4)(x2-4x+16)

播放段落

Example 4
::例4

播放段落

Factor using the sum or difference of cubes: $\begin{align*}125-216x^3\end{align*}$
::使用立方体:125-216x3 的和或差数的系数

播放段落

Factor using the difference of cubes.
::使用立方体差的系数 。

播放段落

$$\begin{align*}125-216x^3 &= 5^3-(6x)^3\\ &= (5-6x)(5^2+(5)(6x)+(6x)^2)\\ &= (5-6x)(25+30x+36x^2)\end{align*}$$
::125-216x3=53-(6x)3=(5-6x)(52+(5)(6x)+(6x)2)=(5-6x)(25+30x+36x2)

播放段落

Example 5
::例5

播放段落

Find the real-number solution to $\begin{align*}27x^3+8=0\end{align*}$ .
::找到 27x3+8=0 的真实数字解决方案。

播放段落

Factor using the sum of cubes and then solve.
::系数,使用立方体的和,然后解答。

播放段落

$$\begin{align*}27x^3+8 &= 0\\ (3x)^3+2^3 &=0\\ (3x+2)(9x^2-6x+4) &= 0\\ x &= -\frac{2}{3}\end{align*}$$
::27x3+8=0(3x)3+23=0(3x+2)(9x2-6x+4)=0x23

播放段落

Review
::回顾

播放段落

Factor each polynomial by using the sum or difference of cubes.
::使用立方体的总和或差数乘以每个多数值。

播放段落
1. $\begin{align*}x^3-27\end{align*}$
   ::x3 - 27
播放段落
2. $\begin{align*}64+x^3\end{align*}$
   ::64+x3 64+x3
播放段落
3. $\begin{align*}32x^3-4\end{align*}$
   ::32x3-4
播放段落
4. $\begin{align*}64x^3+343\end{align*}$
   ::64x3+343
播放段落
5. $\begin{align*}512-729x^3\end{align*}$
   ::512-729x3
播放段落
6. $\begin{align*}125x^4+8x\end{align*}$
   ::125x4+8x
播放段落
7. $\begin{align*}648x^3+81\end{align*}$
   ::648x3+81
播放段落
8. $\begin{align*}5x^6-135x^3\end{align*}$
   ::5x6-135x3
播放段落
9. $\begin{align*}686x^7-1024x^4\end{align*}$
   ::686x7-1024x4

播放段落

Find the real-number solutions for each equation.
::为每个方程寻找真实数字解决方案。

播放段落
10. $\begin{align*}125x^3+1=0\end{align*}$
    ::125x3+1=0
播放段落
11. $\begin{align*}64-729x^3 = 0\end{align*}$
    ::64-729x3=0
播放段落
12. $\begin{align*}8x^4-343x = 0\end{align*}$
    ::8x4 - 343x=0
播放段落
13. Challenge Find ALL solutions (real and imaginary) for $\begin{align*}5x^5+625x^2 = 0\end{align*}$ .
    ::5x5+625x2=0 的“挑战”寻找全部(真实和想象中的)解决方案。
播放段落
14. Challenge Find ALL solutions (real and imaginary) for $\begin{align*}686x^3+2000 = 0\end{align*}$ .
    ::为686x3+2000=0寻找所有解决方案(真实的和想象的)的挑战。
播放段落
15. Real Life Application You have a piece of cardboard that you would like to fold up and make an open (no top) box out of. The dimensions of the cardboard are $\begin{align*}36^{\prime\prime} \times 42^{\prime\prime}\end{align*}$ . Write a factored equation for the volume of this box. Find the volume of the box when $\begin{align*}x = 1, 3,\end{align*}$ and 5.
    ::“真实生活应用程序”中有一个纸板板,您可以折叠,将纸板打开(没有顶部)框。纸板的尺寸是3642。为此框的体积写一个计数方程。在 x=1,3和5时查找框的体积。

播放段落

Review (Answers)
::回顾(答复)

播放段落

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。