节: 使用变形的多面形图 | 2.3 使用变形的多面形图

章节大纲

Penny has been commissioned to paint a large mural on the side of the humane society. The society has a mascot, an African lion that the society supports by donating money to the local zoo for his care. Penny is expected to sketch the lion, submit the sketch to the board of the humane society for approval, and then scale up the drawing to 22 square feet so it will cover the side of the building.
::Penny被委托在人道社会一边画一幅巨大的壁画。社会有一个吉祥物,一个社会支持的非洲狮子,向当地动物园捐钱照顾他。 Penny预计将画出狮子的草图,将草图提交人道社会董事会批准,然后将绘画扩大至22平方英尺,以覆盖建筑物的一侧。

Shortly after Penny actually begins the job of painting the mural, she is visited by the chairman of the board of the humane society. He tells Penny that the Fire Chief has just notified the society that the additional activity the mural is expected to attract means that the building will need another entrance/exit for fire safety. Unfortunately, that means that the mural will need to be moved up and to the right about 5 feet.
::Penny开始画壁画工作后不久,人道社会董事会主席就访问了她。他告诉Penny,消防局长刚刚告诉社会,该壁画预期会吸引更多的活动意味着大楼需要另外的出入口来保障消防安全。不幸的是,这意味着壁画需要往上移动,右移大约5英尺。

What kinds of transformations of complex lines (like the ones in this lesson) will Penny have used by the time she completes the job?
::Penny在完成工作时会使用何种复杂的线条转换(如本课中的线条)?

Graphing Polynomials Using Transformations
::使用变形图绘制多面形图

Polynomial Functions
::多元多边函数

You have already studied many different kinds of functions, for example , constant functions, and quadratic functions. All three these functions belong to a larger group of functions called the polynomial functions .
::您已经研究过许多不同的函数, 例如, 恒定函数和二次函数。所有这些函数都属于更大的一组函数, 称为多函数。

The most simple polynomial is called a power function . A power function is a polynomial of the form $\begin{aligned} f (x) = a x^{n} \end{aligned}$ where $\begin{aligned} a \end{aligned}$ is a real number and $\begin{aligned} n \end{aligned}$ is an integer with $\begin{aligned} n \geq 1 \end{aligned}$ .
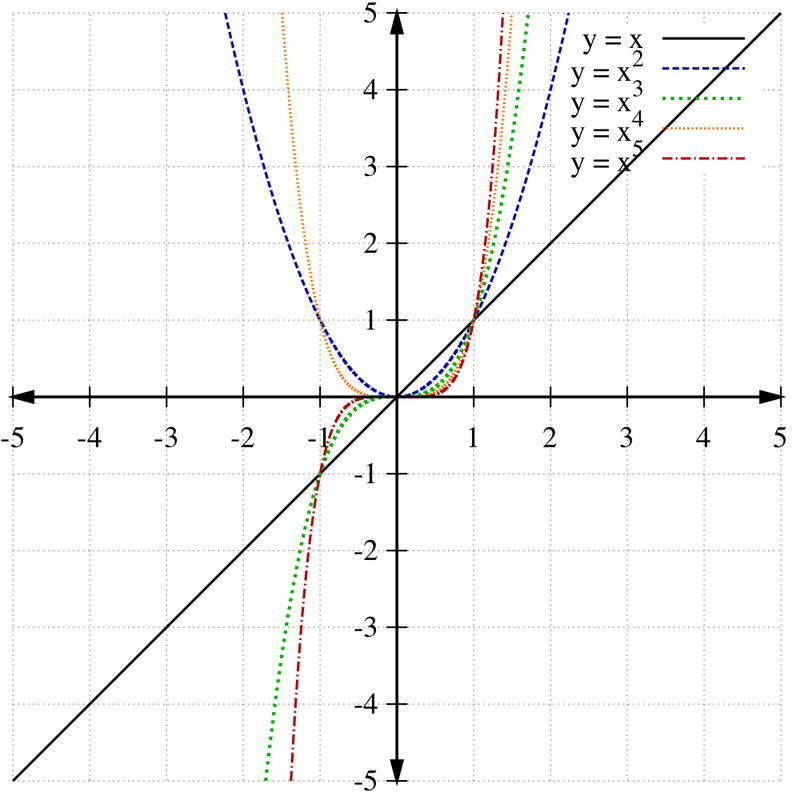
::最简单的多多边函数被称为功率函数。功率函数是窗体 f(x) = 轴的多多边函数,其中一个是真实数字, n是带有 n1 的整数。

If $\begin{aligned} n \end{aligned}$ is even, then the power function is also called “even,” and if $\begin{aligned} n \end{aligned}$ is odd, then the power function is “odd.” The graphs of the first five power functions are shown below.
::如果 n为偶数,则权力函数也称为“偶数 ” , 如果 n为奇数,则权力函数为“奇数 ” 。下面显示前五个权力函数的图示。

Notice that each power function has only one $\begin{aligned} x - \end{aligned}$ and $\begin{aligned} y - \end{aligned}$ intercept , the origin (0, 0).
::注意每个功率函数只有一个 x - 和 y - interview, 来源( 0, 0) 。

The end behavior of a function describes the $\begin{aligned} y - \end{aligned}$ values as $\begin{aligned} x \end{aligned}$ gets very large ( $\begin{aligned} x \to \infty \end{aligned}$ in symbols) or as $\begin{aligned} x \end{aligned}$ gets very small $\begin{aligned} (x \to - \infty) \end{aligned}$ .
::函数的结尾行为描述 Y - 值为 x 变大( 在符号中 x ) 或 x 变小 (x ) 。

For even powers $\begin{aligned} n \end{aligned}$ , the power function $\begin{aligned} f (x) = a x^{n} \end{aligned}$ is U-shaped (like a parabola) and as $\begin{aligned} x \to \infty, f (x) \to \infty \end{aligned}$ . Likewise as $\begin{aligned} x \to - \infty, f (x) \to \infty \end{aligned}$ .
::even power n, 功率函数 f( x) = oxn 是 U 形( 如 parabola) , 和 x , f( x) 。类似 x , f( x) 。

For odd powers $\begin{aligned} n \end{aligned}$ , the power function goes from the third quadrant to the first quadrant (like the line $\begin{aligned} y = x \end{aligned}$ ). As $\begin{aligned} x \to \infty, f (x) \to \infty, \end{aligned}$ and as $\begin{aligned} x \to - \infty, f (x) \to - \infty \end{aligned}$ .
::对于单功率 n , 功率函数从第三个象限到第一个象限( 如线 y=x) 。 as x, f( x) , as x, f( x) , f( x) 。

As with quadratics and , the leading coefficient $\begin{aligned} a \end{aligned}$ changes the vertical “stretching” of power functions.
::与二次曲线和主要系数一样,主要系数改变权力功能的垂直“伸展”。

Graph Polynomial Functions Using Transformations
::使用变形的多面函数

Just like quadratics, polynomial functions can be graphed using transformations of a known graph. The basic transformations are vertical and horizontal shifts and reflections about the $\begin{aligned} x - \end{aligned}$ and $\begin{aligned} y - \end{aligned}$ axis.
::就像二次曲线一样,多元函数可以用已知图形的变换来绘制图表。基本变换是垂直和水平的变换,以及关于 x - 和 y - 轴的反射。

Given a polynomial $\begin{aligned} p (x) \end{aligned}$ and constant real numbers $\begin{aligned} c \end{aligned}$ and $\begin{aligned} a \end{aligned}$
::给定一个多元 p(x) 和恒定实际数 c 和 a

$\begin{aligned} p (x) + c \end{aligned}$ is a vertical shift of the graph of $\begin{aligned} p (x) \end{aligned}$ by $\begin{aligned} c \end{aligned}$ units up (so the function shifts down if $\begin{aligned} c < 0 \end{aligned}$ ).
::p(x)+c 是 p(x) 上方 c 单位的 p(x) +c 图形的垂直移动(因此,如果 c<0 , 函数会向下移动) 。

$\begin{aligned} p (x - c) \end{aligned}$ is a horizontal shift of the graph of $\begin{aligned} p (x) \end{aligned}$ by $\begin{aligned} c \end{aligned}$ units to the right . (So the function shifts left if $\begin{aligned} c < 0 \end{aligned}$ ).
::p( x- c) 是 p( x) 图形中由 c 单位向右水平移动 p( x) 的 p( x) 图表向右水平移动。 (如果 c < 0 ) , 函数向左移动。

$\begin{aligned} - p (x) \end{aligned}$ is a reflection of the graph of $\begin{aligned} p (x) \end{aligned}$ about the $\begin{aligned} x - \end{aligned}$ axis.
:(x) 是 x- 轴的 p(x) 图形的反射。

$\begin{aligned} p (- x) \end{aligned}$ is a reflection of the graph of $\begin{aligned} p (x) \end{aligned}$ about the $\begin{aligned} y - \end{aligned}$ axis.
::p( x) 是 y- 轴的 p( x) 图形的反射。

$\begin{aligned} a p (x) \end{aligned}$ is a vertical stretch by a multiple of $\begin{aligned} a \end{aligned}$ .
::ap(x) 是垂直伸展乘以a的倍数。

$\begin{aligned} p (a x) \end{aligned}$ is a horizontal compression by a multiple of $\begin{aligned} a \end{aligned}$ .
::p( 轴) 是指由 a 乘以的水平压缩。

Examples
::实例

Example 1
::例1

Earlier, you were asked a question about the kinds of transformations of complex lines that Penny will have used in her sketch by the time she completes it.
::早些时候有人问过你 Penny在完成素描时会在草图中使用复杂线的变换类型

When Penny first sketches the lion, she will be (probably unconsciously) applying a vertical and horizontal compression to the sketch, unless she is using a very large piece of paper!
::Penny第一次画狮子时, 她会(可能是无意识地)对草图进行垂直和水平压缩, 除非她用的是一张非常大的纸!

Once the sketch is approved, Penny will then need to greatly stretch the image vertically and horizontally to make the image big enough to cover the side of the building.
::一旦草图获得批准,Penny就会需要大大的垂直和横向拉伸图像,使图像大到足以覆盖建筑物的侧面。

After the Fire Chief visit, Penny was required to apply a horizontal and vertical shift to move the image out of the way of the new door.
::消防队长访问后,Penny被要求进行横向和纵向转变,将图像从新门的道路上移开。

Example 2
::例2

The graph of $\begin{aligned} f (x) \end{aligned}$ is shown below. Use the graph of $\begin{aligned} f (x) \end{aligned}$ to graph $\begin{aligned} f (x + 4) \end{aligned}$ .
::f( x) 的图形显示如下。使用 f( x) 的图形显示 F( x) + 4 的图形。

This is a horizontal shift of $\begin{aligned} f (x) \end{aligned}$ to the left by 4 units.
::这是 f( x) 向左的 4 个单位向左水平移动的 f( x) 。

Example 3
::例3

The graph of $\begin{aligned} f (x) \end{aligned}$ is shown below. Use the graph of $\begin{aligned} f (x) \end{aligned}$ to graph $\begin{aligned} f (- x) + 3 \end{aligned}$ .
::f( x) 的图形显示在下面。使用 f( x) 的图形显示在 f( x) + 3 的图形中。

This is a reflection of $\begin{aligned} f (x) \end{aligned}$ about the $\begin{aligned} y - \end{aligned}$ axis and a vertical shift up by 3 units.
::这是关于y-轴的 f(x) 和垂直移动 3 个单位的反射。

Example 4
::例4

Describe the transformations to a graph of the function $\begin{aligned} y = x^{2} \end{aligned}$ necessary to make a reasonable approximation of $\begin{aligned} f (x) = - x^{4} \end{aligned}$ .
::描述向函数 y=x2 的图形转换,使 f( x) x4 合理近似所需的函数 y=x2 。

Since $\begin{aligned} f (x) = - x^{4} \end{aligned}$ is an even function, the function $\begin{aligned} f (x) = - x^{2} \end{aligned}$ is a reasonable approximation, requiring only a reflection of $\begin{aligned} y = x^{2} \end{aligned}$ across the x-axis .
::由于 f( x) x4 是一个偶数函数, 函数f( x) x2 是一个合理的近似值, 只需要反射 y=x2 横跨 x 轴即可。

Example 5
::例5

Describe the transformations necessary to make a graph of the reference function $\begin{aligned} f (x) = x^{3} \end{aligned}$ look like the graph of $\begin{aligned} y = - 2 x^{3} + 2 \end{aligned}$ .
::描述使引用函数 f( x) = x3 的图形看起来像 y2x3+2 的图形所需的转换。

The transformations required to replicate the function $\begin{aligned} y = - 2 x^{3} + 2 \end{aligned}$ are reflect $\begin{aligned} f (x) = x^{3} \end{aligned}$ across the x-axis, stretch $\begin{aligned} f (x) = - x^{3} \end{aligned}$ by 2, and shift $\begin{aligned} f (x) = - 2 x^{3} \end{aligned}$ upward by 2.
::复制函数 {%% 2x3+2are 反射 f( x) =x3 横跨 x 轴, 伸缩 f( x)\\\ x3x2 和移动 f( x)\\\\\\ 2x3 向上翻转 2 所需的转换。

Example 6
::例6

Describe the end behavior of $\begin{aligned} f (x) = - 7 x^{3} + 6 x^{2} - 3 x \end{aligned}$ using the leading coefficient test.
::使用主要系数测试描述 f( x)\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\F(x)\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\F\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\F\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\

According to the leading coefficient test, given $\begin{aligned} f (x) = a x^{n} \end{aligned}$ where a is the leading coefficient and n is the degree , if n is odd and a is negative, the graph goes up on the left, and down on the right.
::根据主要系数测试,如果 f(x) = 轴,其中, a 是主要系数, n 是程度,如果 n 是奇数, a 是负数,则图向左上, 向右下。

$\begin{aligned} ∴ f (x) = - 7 x^{3} + 6 x^{2} - 3 x \end{aligned}$ grows without bound toward $\begin{aligned} \infty \end{aligned}$ in Quadrant II and grows negatively without bound in Quadrant IV.
::f(x)7x3+6x2-3x在Quadrant II 中未受约束地生长到,而未受Quadrant IV 中的约束而负增长。

Review
::回顾

Given: $\begin{aligned} P (x) = 7 x^{4} - 5 x^{3} + x^{2} - 7 x + 6 \end{aligned}$
::依据: P(x) = 7x4 - 5x3+x2 - 7x+6

State:
::状态 :

The leading term:
::前一任期:

The degree of the polynomial:
::多面性的程度 :

The leading coefficient:
::主要系数:

Describe the transformation given in each question below:
::以下各问题所描述的变换情况如下:

Original Function: $\begin{aligned} g (x) = 3 x^{3} \end{aligned}$ Transformed Function: $\begin{aligned} f (x) = 3 x^{3} + 3 \end{aligned}$
::原始函数: g( x)=3x3 变形函数: f( x)=3x3+3

Original Function: $\begin{aligned} g (x) = 2 x^{3} + 3 \end{aligned}$ Transformed Function: $\begin{aligned} f (x) = 2 x^{3} + 7 \end{aligned}$
::原始函数: g(x)=2x3+3 已变换函数: f(x)=2x3+7

Original Function: $\begin{aligned} g (x) = x^{4} + 2 \end{aligned}$ Transformed Function: $\begin{aligned} f (x) = 3 (x^{4} + 2) \end{aligned}$
::原始函数: g(x)=x4+2 已变换函数: f(x)=3(x4+2)

Original Function: $\begin{aligned} g (x) = 5 x^{3} \end{aligned}$ Transformed Function: $\begin{aligned} f (x) = \frac{1}{2} (x^{3}) \end{aligned}$
::原始函数: g(x)=5x3 变形函数: f(x)=12(x3)

Graph the following by using transformations of parent functions:
::使用父函数转换图如下:

$\begin{aligned} f (x) = 2 x^{5} - 4 \end{aligned}$
:xx)=2x5-4)

$\begin{aligned} f (x) = (x - 4)^{3} + 6 \end{aligned}$
:xx)=(x-4)3+6

$\begin{aligned} f (x) = - 2 x^{4} + x^{2} \end{aligned}$
:xx) 2x4+x2

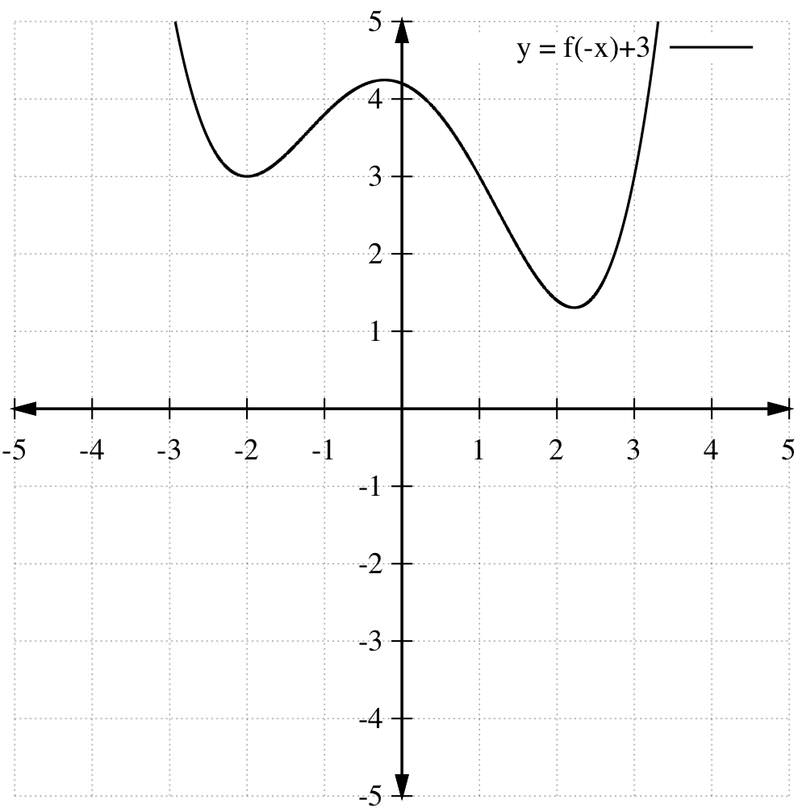
Describe each transformation based on the images below:
::根据以下图像描述每次变换:

From: To:
::发讯人:致:

From: To:
::发讯人:致:

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

章节大纲

Graphing Polynomials Using Transformations ::使用变形图绘制多面形图

Polynomial Functions ::多元多边函数

Graph Polynomial Functions Using Transformations ::使用变形的多面函数

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

Example 5 ::例5

Example 6 ::例6

Review ::回顾

Review (Answers) ::回顾(答复)

Graphing Polynomials Using Transformations
::使用变形图绘制多面形图

Polynomial Functions
::多元多边函数

Graph Polynomial Functions Using Transformations
::使用变形的多面函数

Examples
::实例

Example 1
::例1

Example 2
::例2

Example 3
::例3

Example 4
::例4

Example 5
::例5

Example 6
::例6

Review
::回顾

Review (Answers)
::回顾(答复)