Section: 简缩缩缩缩 | 2.6 静态

Section outline

Working with rational functions is often a matter of finding what the graph isn't as much as finding what it is . By identifying the values that the function cannot have, either as an input or as an output, we restrict the possibilities of what the graph may look like.
::与理性函数一起工作往往需要找到图形与找到它不相干的东西。通过确定函数不能拥有的值,无论是输入还是输出,我们限制了图形外观的可能性。

You have previously graphed rational functions using transformations and horizontal and vertical asymptotes . You may have noted that appear in rational equations when the degree of the numerator is less than or equal to the degree of the denominator.
::您以前曾使用转换以及水平和垂直等同元素绘制过理性函数图。当分子的量小于或等于分母的量时, 您可能已经注意到在理性方程中出现的合理函数。

What happens when the degree of the numerator is greater than the degree of the denominator? How does this situation appear in the graph of the function?
::当分子的程度大于分母的程度时会发生什么情况?这种情况如何出现在函数的图形中?

Oblique Asymptotes
::简缩缩缩缩

Not all asymptotes of rational functions are vertical or horizontal. Let's consider what happens when the degree of the numerator is one greater than the denominator, resulting in a diagonal line known as an oblique or slant asymptote .
::并非所有理性函数的微量都是垂直的或水平的。让我们来考虑当分子的程度大于分母时会发生什么, 从而形成一条被称为斜线或斜线的对角线。

If we look at the graph of the rational function $\begin{aligned} g (x) = \frac{x^{3}}{x^{2} + 1} \end{aligned}$ , we can see that there is no horizontal asymptote of this function.
::如果我们查看理性函数 g( x) =x3x2+1 的图形, 我们可以看到此函数没有水平等同值。

There is no horizontal asymptote in this function because the degree of the numerator is greater than the degree of the denominator.
::3⁄4 ̄ ̧漯B

As a reminder, the following guidelines can help identify the asymptotes of a rational function $\begin{aligned} r (x) = \frac{f (x)}{D (x)} \end{aligned}$ :
::作为提醒,以下指南可以帮助识别 r(x) =f(x)D(x) 的合理函数的微粒:

If the degree of the denominator is greater than the degree of the numerator, then the line $\begin{aligned} y = 0 \end{aligned}$ is a horizontal asymptote.
::如果分母的度大于分子的度,则Y=0线为水平单数。

If the degree of the numerator and the denominator are equal, then the line $\begin{aligned} y = \frac{a}{b} \end{aligned}$ is a horizontal asymptote, where $\begin{aligned} a \end{aligned}$ is the leading coefficient of $\begin{aligned} f (x) \end{aligned}$ , the numerator, and $\begin{aligned} b \end{aligned}$ is the leading coefficient of $\begin{aligned} D (x) \end{aligned}$ , the denominator.
::如果分子和分母的程度相等,则Y=ab线是一个水平的同位数,其中主要系数为 f(x),分子和b是分母D(x)的主要系数。

If the degree of the numerator is larger than the degree of the denominator, then the quotient function, $\begin{aligned} Q (x) \end{aligned}$ , found by dividing the numerator and denominator of the rational function, is an . Recall that for any rational function $\begin{aligned} \frac{f (x)}{D (X)} \end{aligned}$ , you can use polynomial division to re-write that function in the form $\begin{aligned} \frac{f (x)}{D (x)} = Q (x) + \frac{R (x)}{D (x)} \end{aligned}$ where $\begin{aligned} Q (x) \end{aligned}$ is the quotient and $\begin{aligned} R (x) \end{aligned}$ is the remainder.
::如果分子的程度大于分母的程度,那么通过分隔数和理性函数的分母而发现的商数函数 Q(x) 是一个。提醒注意,对于任何合理的函数 f(x)D(X),您可以使用多数值分割法重写以 f(x)D(x) (x)+R(x) D(x) 格式为 Q(x) 是商数和 R(x) 是剩余函数的 f(x) 函数。

Examples
::实例

Example 1
::例1

Earlier, you were given a question about an asymptotic situation .
::早些时候,你被问起一种无药可救的情况

You should have no difficulty with this question now: When the degree of the numerator is greater, there is no horizontal asymptote, but rather a slant or oblique asymptote. It appears as a diagonal line across the graph of the function.
::您现在应该对此问题没有困难: 当分子的量更大时, 没有水平的无线点, 而是倾斜或倾斜的无线点。它作为对角线出现在函数图的对角线上。

Example 2
::例2

Graph $\begin{aligned} g (x) = \frac{x^{2} - 1}{x - 2} \end{aligned}$ .
::图g(x)=x2-1x-2。

First observe that the vertical asymptote is at $\begin{aligned} x = 2 \end{aligned}$ . Notice that the degree of the numerator is greater than the degree of the denominator. We can change the form of the rational expression by long division. You may recall from algebra that can be divided (just like real numbers), and any rational functions can be written as
::首先观察垂直空点为 x=2 。请注意, 分子的程度大于分母的程度。我们可以用长分割来改变理性表达形式。您可以从代数中回忆到可以分割的代数( 和实际数字一样) , 任何合理的函数都可以写成

\begin{aligned} \frac{f (x)}{D (x)} = Q (x) + \frac{R (x)}{D (x)} \end{aligned}

fx)D(x)(x)+R(x)D(x)

Doing the long division here,
::做长师在这里,

\begin{aligned} x + 2 \\ x - 2) \bar{x^{2} + 0 x - 1} \\ \underline{x^{2} - 2 x ↓} \\ 2 x - 1 \\ \underline{2 x - 4} \\ 3 \end{aligned}

::x2x - 2) x2+0x - 1x2 - 2x *2x - 12x - 4_ 3

So in this case, the function $\begin{aligned} g (x) \end{aligned}$ can be rewritten as
::在这种情况下, 函数 g( x) 可以重写为

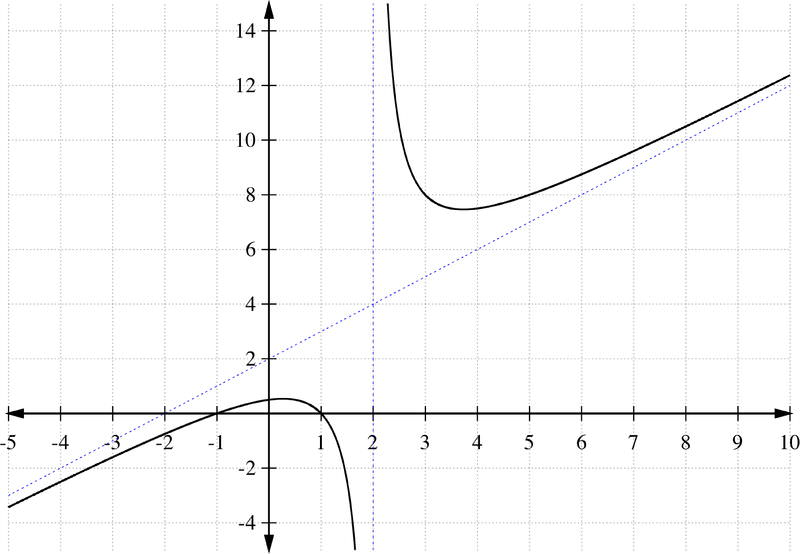
\begin{aligned} g (x) = \frac{x^{2} - 1}{x - 2} = x + 2 + \frac{3}{x - 2} \end{aligned}

::g(x) =x2- 1x-2=x+2+3x-2

The above equation tells us that as $\begin{aligned} x \to \pm \infty \end{aligned}$ , the graph of $\begin{aligned} g (x) = x + 2 + \frac{3}{x - 2} \end{aligned}$ gets closer and closer to the line $\begin{aligned} y = x + 2 \end{aligned}$ . Why? Suppose we let $\begin{aligned} x \end{aligned}$ be a big number, i.e. $\begin{aligned} x = 1, 000, 000 \end{aligned}$ . Then the remainder of this rational function becomes $\begin{aligned} \frac{3}{999, 998} \approx 0 \end{aligned}$ and we are left with $\begin{aligned} x + 2 \end{aligned}$ . We call this line an oblique asymptote and it is indicated by the dashed line in the image below.
::以上方程式告诉我们,作为 x, g(x) =x+2+3x-2 的图形越来越接近 y=x+2 。为什么? 假设我们让 x 是一个大数字, 即 x= 1000000,000 。那么这个理性函数的剩余部分变成 3999, 998 0 , 剩下的是 x+2 。我们称这条线为斜线, 用下面图像中的破折线来表示。

Example 3
::例3

Identify the oblique asymptote of $\begin{aligned} g (x) = \frac{x^{3}}{x^{2} + 1} \end{aligned}$ .
::识别 g( x) =x3x2+1 的斜体星点数。

By polynomial division we have,
::我们拥有的一元形分裂,

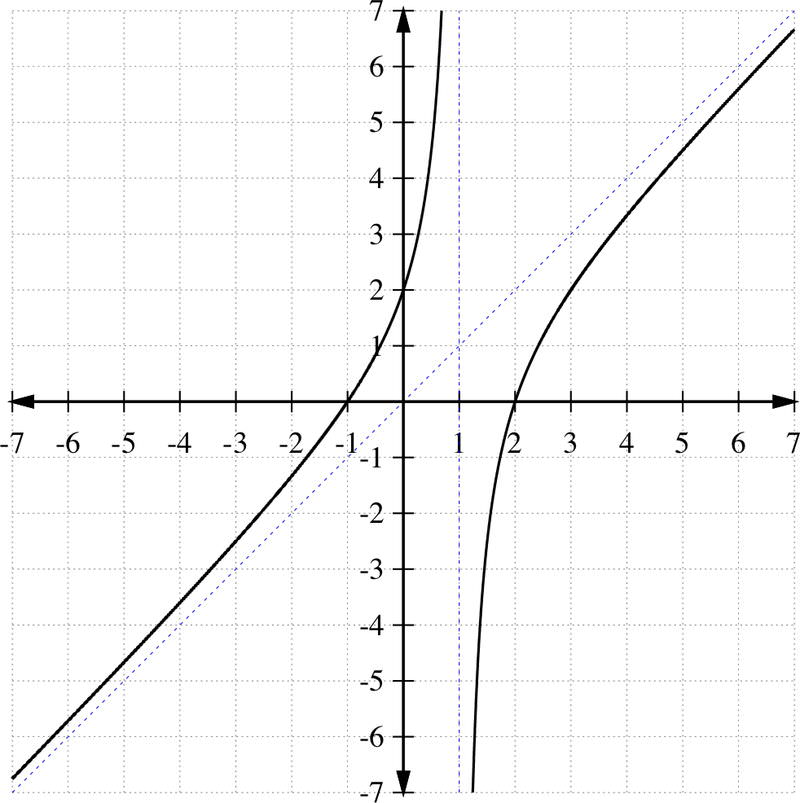
\begin{aligned} x \leftarrow Quotient \\ x^{2} + 1) \bar{x^{3} + 0 x^{2} + 0 x + 0} \leftarrow Dividend \\ \underline{x^{3} + x} \\ - x \leftarrow Remainder \end{aligned}

::================================================================================================================================================ =================================================================================== ===========================================

So $\begin{aligned} g (x) = x - \frac{x}{x^{2} + 1} \end{aligned}$ . This tells us that the line $\begin{aligned} y = x \end{aligned}$ is an oblique asymptote of $\begin{aligned} g (x) \end{aligned}$ .
::g(x) =x-xx2+1。这告诉我们, y=x 是 g(x) 的斜线。

Notice that the oblique asymptotes of a rational function also describe the end behavior of the function. That is, as you “zoom out” from the graph of a rational function it looks like a line or the function defined by $\begin{aligned} Q (x) \end{aligned}$ in $\begin{aligned} \frac{f (x)}{D (x)} = Q (x) + \frac{R (x)}{D (x)} \end{aligned}$ .
::请注意, 理性函数的斜线单位数也描述函数的结束行为。也就是说, 您从理性函数的图形中“ 退出 ” , 它看起来像一条线或 F( x) D( x) ( x) +R( x) D( x) 定义的 Q( x) 函数的函数。

Example 4
::例4

Find the oblique asymptote of $\begin{aligned} f (x) = \frac{3 x^{3} - 5 x^{2} + 2}{x^{2} - 3 x} \end{aligned}$ . Sketch a graph of $\begin{aligned} f (x) \end{aligned}$ .
::查找 f( x) = 3x3 - 5x2+2x2 - 3x. 绘制 f( x) 的图形。

Using polynomial long division , $\begin{aligned} f (x) = 3 x + 4 + \frac{4 x^{2}}{x^{2} - 3 x} \end{aligned}$ . Thus, the line $\begin{aligned} y = 3 x + 4 \end{aligned}$ is an oblique asymptote of $\begin{aligned} f (x) \end{aligned}$ .
::因此,y=3x+4是f(x)的斜线。

To sketch the graph we can find the by setting the denominator equal to zero,
::为了绘制图表,我们可以通过设定分母等于零来找到它,

\begin{aligned} x^{2} - 3 x & = 0 \\ x (x - 3) & = 0 \end{aligned}

::x2-3x=0x(x-3)=0

So the two vertical asymptotes are $\begin{aligned} x = 0 \end{aligned}$ and $\begin{aligned} x = 3 \end{aligned}$ .
::因此,两个垂直的单位数是 x=0 和 x=3 。

$\begin{aligned} f (0) \end{aligned}$ is undefined , so there is no $\begin{aligned} y - \end{aligned}$ intercept . Also, there is no simple way to solve for the roots (setting the numerator equal to zero), but we can see by inspection that $\begin{aligned} f (1) = 0 \end{aligned}$ . To get an idea of the shape of the graph we will make a table of a few test points. We used a calculator to evaluate decimal values of $\begin{aligned} x \end{aligned}$ in $\begin{aligned} f (x) \end{aligned}$ .
::f( 0) 尚未定义, 因此没有 Y - intercut 。另外, 根没有简单的解答方法( 将分子数设为零) , 但我们通过检查可以看到 f(1)=0 。要了解图形的形状, 我们将绘制几个测试点的表格。我们使用计算器来评估 f( x) 中的 x 小数值。

\begin{aligned} x & - 2 & - 1 & - 0.1 & 1 & 2 & 4 & 3.5 & 5 & 6 \\ f (x) & - 4.2 & - 1.5 & 66.48 & 0 & - 3 & 28.5 & 39.6 & 25.2 & 26.1 \end{aligned}

::X-2-1-0.11 2 43.5 5 6f(x)-42-1.566. 480-328.539.625.226.1

Finally we use all of this information to make a sketch of the graph of $\begin{aligned} f (x) \end{aligned}$ :
::最后,我们利用所有这些信息来绘制f(x) 图表的草图:

Example 5
::例5

Graph $\begin{aligned} f (x) = \frac{x^{2} - x - 2}{x - 1} \end{aligned}$ .
::图f(x)=x2-x-2x-1。

The vertical asymptote here is $\begin{aligned} x = 1 \end{aligned}$ since a 1 for x in the denominator makes the fraction undefined.
::这里的垂直位数为 x=1, 因为分母中的 x 1 使分数未定义。

To find the x - intercepts , factor the numerator:

\begin{aligned} f (x) = \frac{x^{2} - x - 2}{x - 1} = \frac{(x - 2) (x + 1)}{x - 1} \end{aligned}

::要找到 x 界面, 请乘以数数 : f( x) =x2 - x2 - x-2x- 1= (x- 2) (x+1) x- 1

Notice that the $\begin{aligned} x - \end{aligned}$ intercepts are at $\begin{aligned} x = 2 \end{aligned}$ and $\begin{aligned} x = - 1 \end{aligned}$ since those are the values which make $\begin{aligned} \frac{(x - 2) (x + 1)}{x - 1} = 0 \end{aligned}$ true.
::注意 x- internews 是在 x=2 和 x=1 的值, 因为这些值使 (x- 2 (x+1)x- 1=0) 成为真实值。

To identify the oblique asymptote, we divide $\begin{aligned} \frac{x^{2} - x - 2}{x - 1} \end{aligned}$ using polynomial long division, yielding:

\begin{aligned} f (x) = x - \frac{2}{x - 1} \end{aligned}

::为了确定斜形无星图,我们使用多数值长的分割法将 x2 - x - x2 - 2x - 1 分隔开来,产生 : f( x) =x - 2x - 1

Recall that the whole (non-fractional) part of the quotient indicates the oblique asymptote, so we have $\begin{aligned} y = x \end{aligned}$ .
::回顾商数的整个(非违规)部分表示斜线渐行渐远,所以我们有y=x。

Make a table of points, then sketch the graph using those points and the asymptote.
::绘制一个点表,然后用这些点和零点绘制图表。

x	f ( x )
2	0
(-1)	0
0	2
3	0

Example 6
::例6

Identify the asymptote(s) of $\begin{aligned} \frac{1 + x^{2}}{x} + \frac{x^{2} - 1}{x} + \frac{x}{x^{2} - 1} \end{aligned}$ .
::识别 1+x2x+x2-2-1x+x22-2-1的空位数。

First, we need to simplify the expressions $\begin{aligned} \frac{1 + x^{2}}{x} + \frac{x^{2} - 1}{x} \end{aligned}$
::首先,我们需要简化表达式 1+x2x+x2-1x

Since the denominators are the same, we can just add the numerators, yielding: $\begin{aligned} \frac{1 + x^{2} + x^{2} - 1}{x} ==> 2 x \end{aligned}$
::由于分母是相同的,我们可以加入数解器,产生:1+x2+x2+x2-1x%2x

Now we have: $\begin{aligned} 2 x + \frac{x}{x^{2} - 1} \end{aligned}$ convenient! No polynomial division necessary!
::现在我们有了: 2x+2x2-2-1方便! 没有必要的多元分裂 !

The slant asymptote is $\begin{aligned} y = 2 x \end{aligned}$
::倾斜渐变为 Y=2x

Looking at $\begin{aligned} 2 x + \frac{x}{x^{2} - 1} \end{aligned}$ we can see that the vertical asymptotes are at $\begin{aligned} x = 1 \end{aligned}$ and $\begin{aligned} x = - 1 \end{aligned}$
::查看 2x+xx2-2- 1 时,我们可以看到垂直微粒为 x=1 和 x1 。

Looking at the original form: $\begin{aligned} \frac{1 + x^{2}}{x} + \frac{x^{2} - 1}{x} \end{aligned}$ we can see a hole in the graph at (0, 0)
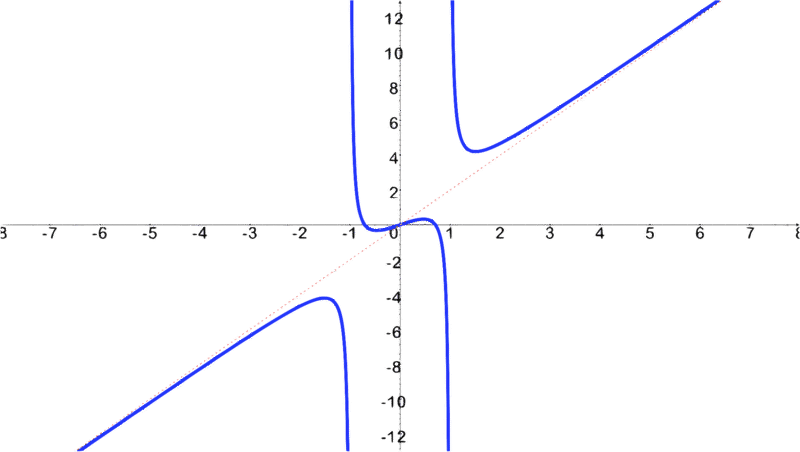
::查看原始窗体的原始窗体:1+x2x+x2-2-1x,我们可以看到图形中的洞( 0, 0)

The sketch of the graph would look like this:
::图表的草图看起来是这样的:

Review
::回顾

What has to be true of the degree of the numerator and the denominator for an asymptote to be called oblique or slant?
::分子的程度和分母的分母如何才能被称作斜斜或倾斜?

Find the slant asymptotes:
::查找倾斜的零星数 :

$\begin{aligned} y = \frac{3 x^{3}}{x^{2} - 1} \end{aligned}$
::y= 3x3x2 - 1

$\begin{aligned} y = \frac{2 x^{2}}{x + 1} \end{aligned}$
::y= 2x2x+1

$\begin{aligned} y = \frac{2 x^{3} - 7 x^{2} - 4}{(x + 3) (x - 1)} \end{aligned}$
::y=2x3- 7x2- 4(x+3)(x-1)

$\begin{aligned} y = \frac{(2 x) (x + 11)}{x - 4} \end{aligned}$
::y=( 2x)( x+11) x- 4

$\begin{aligned} y = \frac{x^{3} - x + 3}{x^{2} + x - 2} \end{aligned}$
::y=x3-x+3x2+x-2 y=x3-x+3x2+x-2

$\begin{aligned} f (x) = \frac{x^{2} - 4}{x} \end{aligned}$
:xx) =x2-4x

$\begin{aligned} f (x) = \frac{x^{3} - 3}{x^{2}} \end{aligned}$
:xx) =x3 - 3x2

$\begin{aligned} y = \frac{3 x^{3} - 3}{2 x^{2}} \end{aligned}$
::y= 3x3 - 32x2 y= 3x3 - 32x2

Find all intercepts and asymptotes for the graphs of the following rational functions and use that information to help you sketch the graphs of the functions.
::为以下理性函数的图形查找所有拦截和静态图,并使用此信息帮助您绘制函数的图形。

$\begin{aligned} f (x) = \frac{2 x^{2}}{1 - x} \end{aligned}$
:xx)=2x21-x)

$\begin{aligned} f (x) = \frac{x^{3} - 3 x^{2}}{x^{2} - 1} \end{aligned}$
:xx) =x3 - 3x2x2 - 1

$\begin{aligned} f (x) = \frac{x^{3} - 1}{x^{2} - x - 2} \end{aligned}$
:xx) =x3 - 1x2 -x2

$\begin{aligned} f (x) = \frac{x^{3} - 1}{2 (x^{2} - 1)} \end{aligned}$
:xx) =x3- 12(x2- 1)

$\begin{aligned} y = \frac{2 x^{2}}{x - 3} \end{aligned}$
::y= 2x2x- 3

$\begin{aligned} y = \frac{3 x^{2}}{x + 2} \end{aligned}$
::y= 3x2x+2

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

Section outline

Oblique Asymptotes ::简缩缩缩缩

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

Example 5 ::例5

Example 6 ::例6

Review ::回顾

Review (Answers) ::回顾(答复)