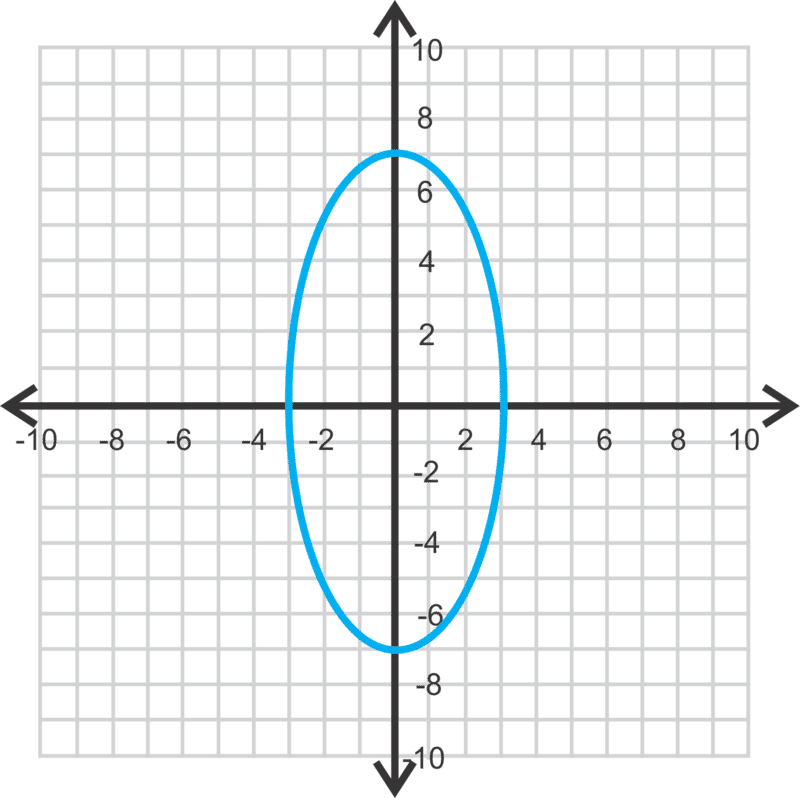
Section: 位于起源点的椭圆 | 10.5 以原产地为中心

Section outline

Your homework assignment is to draw the ellipse $\begin{align*}16x^2 + 4y^2 = 144\end{align*}$ . Where will the foci of your graph be located?
::您的作业任务是绘制 16x2+4y2=144 的椭圆。您的图表的方位将在哪里 ?

Ellipses Centered at the Origin
::位于起源点的椭圆

The third conic section is an ellipse. Recall that a circle is when a plane sliced through a cone and that plane is parallel to the base of the cone. An ellipse is formed when that plane is not parallel to the base. Therefore, a circle is actually a more specific version of an ellipse.
::第三个二次二次曲线区域是椭圆。回顾一个圆圈是指一个平面通过锥体切片,该平面与锥体的底部平行。当该平面与底部不平行时,会形成椭圆。因此,一个圆圈实际上是一个更具体的椭圆版本。

By definition, an ellipse is the set of all points such that the sum of the distances from two fixed points, called foci (the plural of focus ), is constant.
::顾名思义,椭圆是所有点的组合,以便两个固定点(称为焦点复数)的距离总和保持不变。

Drawing an Ellipse
::绘制椭圆

We will use the definition of an ellipse to draw an ellipse.
::我们将使用椭圆的定义来绘制椭圆。

Step 1: On a piece of graph paper, draw a set of axes and plot $\begin{align*}(-2, 0)\end{align*}$ and $\begin{align*}(2, 0)\end{align*}$ . These will be the foci.
::第1步:在一张图表纸上,绘制一组轴和绘图(-2,0)和(2,0)。

Step 2: From the definition, we can conclude a point $\begin{align*}(x, y)\end{align*}$ is on an ellipse if the sum of the distances is always constant. In the picture, $\begin{align*}d_1+d_2=r\end{align*}$ and $\begin{align*}g_1+g_2=r\end{align*}$ .
::第2步:从定义中,我们可以得出一个点(x,y)在椭圆上,如果距离总和总是不变。在图片中, d1+d2=r和 g1+g2=r。

Step 3: Determine how far apart the foci are. Then, find $\begin{align*}d_1\end{align*}$ and $\begin{align*}d_2\end{align*}$ .
::步骤 3 : 确定方形之间的距离。然后找到 d1 和 d2 。

Step 4: Determine if the point $\begin{align*}(-2, 3)\end{align*}$ is on the ellipse.
::第4步:确定点(-2.3)是否在椭圆上。

In this concept, the center of an ellipse will be $\begin{align*}(0, 0)\end{align*}$ . An ellipse can have either a vertical or horizontal orientation (see below). There are always two foci and they are on the major axis . The major axis is the longer of the two axes that pass through the center of an ellipse. Also on the major axis are the vertices , which its endpoints and are the furthest two points away from each other on an ellipse. The shorter axis that passes through the center is called the minor axis , with endpoints called co-vertices . The midpoint of both axes is the center.
::在这个概念中,椭圆的中心将是(0,0) 椭圆的垂直方向或水平方向(见下文)。椭圆可以有垂直方向或水平方向( 参见下面)。始终有两个角, 它们位于主轴上。主要的轴是穿过椭圆中心的两个轴的长度。在主要轴上还有脊椎, 其端点和在椭圆上距离对方最远的两点。穿过中心的短轴被称为小轴, 端点称为共同垂直。两个轴的中点是中点。

, Centered at the Origin
$\begin{align}\frac{x^2}{a^2}+ \frac{y^2}{b^2}=1\end{align}$	HORIZONTAL ::洪都拉斯 major axis is the $\begin{align}x\end{align}$ -axis with length $\begin{align}2a\end{align}$ . ::主轴是长度为 2a 的 X 轴。 minor axis is the $\begin{align}y\end{align}$ -axis with length $\begin{align}2b\end{align}$ . ::次要轴是长度为 2b 的 Y 轴。
$\begin{align}\frac{x^2}{b^2}+ \frac{y^2}{a^2}=1\end{align}$	VERTICAL ::核查、核查、核查、核查、 major axis is the $\begin{align}y\end{align}$ -axis with length $\begin{align}2a\end{align}$ . ::主轴是长度为 2a 的 Y 轴。 minor axis is the $\begin{align}x\end{align}$ -axis with length $\begin{align}2b\end{align}$ . ::次要轴是长度为2b的 X 轴。

Other Important Facts
::其他重要事实

$\begin{align*}a\end{align*}$ is ALWAYS greater than $\begin{align*}b\end{align*}$ . If they are equal, we have a circle.
::a AlwaysWAYS 大于 b。如果等值,我们有一个圆。

The foci, vertices, and co-vertices relate through a version of the Pythagorean Theorem: $\begin{align*}c^2=a^2-b^2\end{align*}$
::方形、脊椎和共白则通过版本的《毕达哥里安理论论:c2=a2-b2》进行关联。

Let's find the vertices, co-vertices, and foci of $\begin{align*}\frac{x^2}{64}+ \frac{y^2}{25}=1\end{align*}$ . Then, let's graph the ellipse.
::让我们找到 x264+y225=1 的顶点、共垂直点和角点。然后,让我们来绘制椭圆图。

First, we need to determine if this is a horizontal or vertical ellipse. Because $\begin{align*}64 > 25\end{align*}$ , we know that the ellipse will be horizontal. Therefore, $\begin{align*}a^2=64\end{align*}$ making $\begin{align*}a=\sqrt{64}=8\end{align*}$ and $\begin{align*}b^2=25\end{align*}$ , making $\begin{align*}b=\sqrt{25}=5\end{align*}$ . Using the pictures above, the vertices will be $\begin{align*}(8, 0)\end{align*}$ and $\begin{align*}(-8, 0)\end{align*}$ and the co-vertices will be $\begin{align*}(0, 5)\end{align*}$ and $\begin{align*}(0, -5)\end{align*}$ .
::首先,我们需要确定这是水平椭圆还是垂直的椭圆。因为 64> 25, 我们知道椭圆是水平的。因此, a2=64 making a= 64=8 和 b2=25, make b=25=5 上面的图片, 脊椎将是 8,0 和 (-8,0) , 双尾是 (0,5) 和 (0, 5) 。

To find the foci, we need to use the equation $\begin{align*}c^2=a^2-b^2\end{align*}$ and solve for $\begin{align*}c\end{align*}$ .
::要找到方块,我们需要使用方程式 c2=a2 -b2 并解决 c。

\begin{aligned} c^{2} & = 64 - 25 = 39 \\ c & = \sqrt{39} \end{aligned}

$\begin{align*}c^2&=64-25=39 \\ c&=\sqrt{39}\end{align*}$
::c2=64-25=39c=39

The foci are $\begin{align*}\left(\sqrt{39},0\right)\end{align*}$ and $\begin{align*}\left(- \sqrt{39},0\right)\end{align*}$ .
::底部是(39,0)和(-39,0)。

To graph the ellipse, plot the vertices and co-vertices and connect the four points to make the closed curve.
::绘制椭圆图,绘制脊椎和共同垂直图,并连接四点,以形成封闭曲线。

Now, let's graph $\begin{align*}49x^2+9y^2=441\end{align*}$ and identify the foci.
::现在,让我们用图49x2+9y2=441 来识别方位。

This equation is not in standard form. To rewrite it in standard form, the right side of the equation must be 1. Divide everything by 441.
::此方程式不是标准格式。要重写标准格式, 方程式的右侧必须是 1. 将所有方程式除以441 。

\begin{aligned} \frac{49 x^{2}}{441} + \frac{9 y^{2}}{441} & = \frac{441}{441} \\ \frac{x^{2}}{9} + \frac{y^{2}}{49} & = 1 \end{aligned}

$\begin{align*}\frac{49x^2}{441}+ \frac{9y^2}{441}&= \frac{441}{441} \\ \frac{x^2}{9}+ \frac{y^2}{49}&=1\end{align*}$
::49x2441+9y2441=441441x29+y249=1

Now, we can see that this is a vertical ellipse, where $\begin{align*}b=3\end{align*}$ and $\begin{align*}a=7\end{align*}$ .
::现在,我们可以看到,这是一个垂直的椭圆, b=3和a=7。

To find the foci, use $\begin{align*}c^2=a^2-b^2\end{align*}$ .
::要找到角,请使用 c2=a2-b2。

\begin{aligned} c^{2} & = 49 - 9 = 40 \\ c & = \sqrt{40} = 2 \sqrt{10} \end{aligned}

$\begin{align*}c^2&=49-9=40 \\ c&=\sqrt{40}=2\sqrt{10}\end{align*}$
::c2=49-9=40c=40=210

The foci are $\begin{align*}\left(0,2\sqrt{10}\right)\end{align*}$ and $\begin{align*}\left(0,-2\sqrt{10}\right)\end{align*}$ .
::表面为(0,210)和(0,-210)。

Finally, let's write equations for the with the given characteristics below and centered at the origin.
::最后,让我们写一个方程式, 以下面的特性为主, 以源代码为主。

In either part, you may wish to draw the ellipse to help with the orientation.
::在任一部分,您都不妨绘制椭圆来帮助指导方向。

vertex: $\begin{align*}(-6, 0)\end{align*}$ , co-vertex: $\begin{align*}(0, 4)\end{align*}$
::顶点 - 6,0) 共顶点 : (0,4)

We can conclude that $\begin{align*}a=6\end{align*}$ and $\begin{align*}b=4\end{align*}$ . The ellipse is horizontal, because the larger value, $\begin{align*}a\end{align*}$ , is the $\begin{align*}x\end{align*}$ -value of the vertex. The equation is $\begin{align*}\frac{x^2}{36}+ \frac{y^2}{16}=1\end{align*}$ .
::我们可以得出 a=6 和 b=4。椭圆是水平的, 因为较大的值, a, 是顶点的 x 值。方程式是 x236+y216=1 。

vertex: $\begin{align*}(0, 9)\end{align*}$ , focus: $\begin{align*}(0, -5)\end{align*}$
::顶点0,9),重点0,-5)

We know that $\begin{align*}a=9\end{align*}$ and $\begin{align*}c=5\end{align*}$ and that the ellipse is vertical. Solve for $\begin{align*}b\end{align*}$ using $\begin{align*}c^2=a^2-b^2\end{align*}$
::我们知道 a=9 和 c=5, 椭圆是垂直的。使用 c2=a2 - b2 解决 b 。

\begin{aligned} 5^{2} & = 9^{2} - b^{2} \\ 25 & = 81 - b^{2} \\ b^{2} & = 56 \to b = 2 \sqrt{14} \end{aligned}

$\begin{align*}5^2&=9^2-b^2 \\ 25&=81-b^2 \\ b^2&=56 \rightarrow b=2\sqrt{14}\end{align*}$
::52=92-b225=81-b2b2=56b=214

The equation is $\begin{align*}\frac{x^2}{56}+ \frac{y^2}{81}=1\end{align*}$
::方程式是 x256+y281=1

Examples
::实例

Example 1
::例1

Earlier, you were asked to determine where the foci of your graph would be located.
::早些时候,有人要求你确定你图表的方位位置

This equation is not in standard form. To rewrite it in standard form, the right side of the equation must be 1. Divide everything by 144.
::此方程式不是标准格式。要重写标准格式, 方程式的右侧必须是 1. 将每方除以144 。

\begin{aligned} \frac{16 x^{2}}{144} + \frac{4 y^{2}}{144} & = \frac{144}{144} \\ \frac{x^{2}}{9} + \frac{y^{2}}{36} & = 1 \end{aligned}

$\begin{align*}\frac{16x^2}{144}+ \frac{4y^2}{144}&= \frac{144}{144} \\ \frac{x^2}{9}+ \frac{y^2}{36}&=1\end{align*}$
::16x2144+4y2144=144144x29+y236=1

Now, we can see that this is a vertical ellipse, where $\begin{align*}b=3\end{align*}$ and $\begin{align*}a=6\end{align*}$ .
::现在,我们可以看到,这是一个垂直的椭圆, b=3和a=6。

To find the foci, use $\begin{align*}c^2=a^2-b^2\end{align*}$ .
::要找到角,请使用 c2=a2-b2。

\begin{aligned} c^{2} & = 36 - 9 = 27 \\ c & = \sqrt{27} = 3 \sqrt{3} \end{aligned}

$\begin{align*}c^2&=36-9=27 \\ c&=\sqrt{27}=3\sqrt{3}\end{align*}$
::c2=36-9=27c=27=33

The foci are therefore $\begin{align*}\left(0,3\sqrt{3}\right)\end{align*}$ and $\begin{align*}\left(0,-3\sqrt{3}\right)\end{align*}$ .
::因此,面为(0,33)和(0,33)。

Example 2
::例2

Find the vertices, co-vertices, and foci of $\begin{align*}\frac{x^2}{4}+ \frac{y^2}{36}=1\end{align*}$ . Then, graph the equation.
::查找 x24+y236=1 的顶点、共垂直点和角。然后, 绘制公式。

Because the larger number is under $\begin{align*}y^2\end{align*}$ , the ellipse is vertical. Therefore, $\begin{align*}a=6\end{align*}$ and $\begin{align*}b^2\end{align*}$ . Use $\begin{align*}c^2=a^2-b^2\end{align*}$ to find $\begin{align*}c\end{align*}$ .
::因为数量较大的是Y2, 椭圆是垂直的。因此, a=6 和 b2. 使用 c2=a2 - b2 来查找 c。

\begin{aligned} c^{2} & = 6^{2} - 2^{2} = 36 - 4 = 32 \\ c & = \sqrt{32} = 4 \sqrt{2} \end{aligned}

$\begin{align*}c^2&=6^2-2^2=36-4=32 \\ c&=\sqrt{32}=4\sqrt{2}\end{align*}$
::c2=62-22=36-4=32c=32=42

vertices: $\begin{align*}(0, 6)\end{align*}$ and $\begin{align*}(0, -6)\end{align*}$
::顶点0,6)和(0,-6)

co-vertices: $\begin{align*}(2, 0)\end{align*}$ and $\begin{align*}(-2, 0)\end{align*}$
::共同垂直数2,0)和(-2,0)

foci: $\begin{align*}\left(0,4\sqrt{2}\right)\end{align*}$ and $\begin{align*}\left(0,-4\sqrt{2}\right)\end{align*}$
::foci: (0,42)和(0,-42)

Example 3
::例3

Graph $\begin{align*}49x^2+64y^2=3136\end{align*}$ and find the foci.
::图49x2+64y2=3136,找到角。

Rewrite $\begin{align*}49x^2+64y^2=3136\end{align*}$ in standard form.
::以标准格式重写 49x2+64y2=3136 。

\begin{aligned} \frac{49 x^{2}}{3136} + \frac{64 y^{2}}{3136} & = \frac{3136}{3136} \\ \frac{x^{2}}{64} + \frac{y^{2}}{49} & = 1 \end{aligned}

$\begin{align*}\frac{49x^2}{3136}+ \frac{64y^2}{3136}&=\frac{3136}{3136} \\ \frac{x^2}{64}+ \frac{y^2}{49}&=1\end{align*}$
::49x23136+64y23136=313636x264+y249=1

This ellipse is horizontal with $\begin{align*}a=8\end{align*}$ and $\begin{align*}b=7\end{align*}$ . Find $\begin{align*}c\end{align*}$ .
::此椭圆是水平水平的, a=8 和 b=7. 查找 c。

\begin{aligned} c^{2} & = 64 - 49 = 15 \\ c & = \sqrt{15} \end{aligned}

$\begin{align*}c^2&=64-49=15 \\ c&=\sqrt{15}\end{align*}$
::c2=64-49=15c=15

The foci are $\begin{align*}\left(- \sqrt{15},0\right)\end{align*}$ and $\begin{align*}\left(\sqrt{15},0\right)\end{align*}$ .
::面部是(-1,5)和(15,0)。

Example 4
::例4

Find the equation of the ellipse with co-vertex $\begin{align*}(0, -7)\end{align*}$ , focus $\begin{align*}(15, 0)\end{align*}$ and centered at the origin.
::查找椭圆的等离子方程式,以共同顶点(0,-7)为焦点(15,0),以原点为中心。

Because the co-vertex is $\begin{align*}(0, -7), b = 7\end{align*}$ and the ellipse is horizontal. From the foci, we know that $\begin{align*}c = 15\end{align*}$ . Find $\begin{align*}a\end{align*}$ .
::因为共同顶点是 (0, -7, b=7) , 椭圆是水平的。从顶部, 我们知道 c=15, 找到一个。

\begin{aligned} 15^{2} & = a^{2} - 7^{2} \\ a^{2} & = 225 + 49 = 274 & The equation is \frac{x^{2}}{274} + \frac{y^{2}}{49} = 1. \\ a & = \sqrt{274} \end{aligned}

$\begin{align*}15^2&=a^2-7^2 \\ a^2&=225+49=274 && \text{The equation is} \ \frac{x^2}{274}+ \frac{y^2}{49}=1. \\ a&=\sqrt{274}\end{align*}$
::152=a2-72a2=225+49=274 方程式为 x2274+y249=1.a=274

Review
::回顾

Find the vertices, co-vertices, and foci of each ellipse below. Then, graph.
::找到下面每个椭圆的脊椎, 共同的脊椎, 和角。然后, 图表。

$\begin{align*}\frac{x^2}{9}+ \frac{y^2}{16}=1\end{align*}$
::x29+y216=1

$\begin{align*}4x^2+25y^2=100\end{align*}$
::4x2+25y2=100

$\begin{align*}\frac{x^2}{64}+y^2=1\end{align*}$
::x264+y2=1

$\begin{align*}81x^2+100y^2=8100\end{align*}$
::81x2+100y2=8100

$\begin{align*}\frac{x^2}{49}+ \frac{y^2}{16}=1\end{align*}$
::x249+y216=1

$\begin{align*}121x^2+9y^2=1089\end{align*}$
::121x2+9y2=1089

Find the equation of the ellipse, centered at the origin, with the given information.
::查找椭圆的方程, 以来源为中心, 并使用给定的信息。

vertex: $\begin{align*}(-3, 0)\end{align*}$ co-vertex: $\begin{align*}(0, 1)\end{align*}$
::顶点 - 3,0) 共同顶点 : (0,1)

co-vertex: $\begin{align*}(7, 0)\end{align*}$ major axis: 18 units
:7,0)主要轴:18个单位

vertex: $\begin{align*}(0, 5)\end{align*}$ minor axis: 4 units
::顶点: (0,5) 小轴: 4 个单位

vertex: $\begin{align*}(0, 6)\end{align*}$ co-vertex: $\begin{align*}(-2, 0)\end{align*}$
::顶点 : (0,6) 共同顶点 -2,0)

co-vertex: $\begin{align*}(17, 0)\end{align*}$ focus: $\begin{align*}(0, 17)\end{align*}$
::共同反差: (17,0) 焦点: (0,17)

vertex: $\begin{align*}(4, 0)\end{align*}$ focus: $\begin{align*}(-3, 0)\end{align*}$
::顶点: (4,0) 焦点-3,0)

co-vertex: $\begin{align*}(-6, 0)\end{align*}$ focus: $\begin{align*}(0, 5)\end{align*}$
:- 6,0) 焦点: (0,5)

focus: $\begin{align*}(0, -9)\end{align*}$ minor axis: 16 units
::焦点: (0,-) 次要轴: 16 个单位

Real Life Application A portion of the backyard of the White House is called The Ellipse. The major axis is 1058 feet and the minor axis is 903 feet. Find the equation of the horizontal ellipse, assuming it is centered at the origin.
::白宫后院的一部分“真实生活应用程序”被称为“椭圆 ” 。主轴为1 058英尺,小轴为903英尺。找到水平椭圆的方程式, 假设以原为中心。

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

Section outline

Ellipses Centered at the Origin ::位于起源点的椭圆

Drawing an Ellipse ::绘制椭圆

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

Review ::回顾

Review (Answers) ::回顾(答复)