复数数

播放段落

Plotting points was something you did back in early algebra, and it likely seems pretty simple now. For instance, plotting the point (4, 5) meant starting at the origin and moving 4 units to the right - the x direction, and 5 units up - the y direction.
::绘图点是你在早期代数时做过的, 现在看起来似乎很简单。 例如, 绘制点( 4, 5) 意味着从起始点开始, 向右移动 4 个单位- x 方向, 向上移动 5 个单位- y 方向 。

播放段落

In this lesson, one of the things we will consider is the graphing of complex numbers such as $\begin{align*}4 +3i\end{align*}$ .
::在这个教训中,我们将要考虑的一件事是绘制4+3i等复杂数字的图表。

播放段落

In essence it doesn't sound that hard, but which direction would you move 3 imaginary units?
::本质上,它听起来并不那么难, 但哪个方向你会移动 3个假想单位?

播放段落

Complex Numbers
::复数数

播放段落

Sometimes when you solve a quadratic equation, the solution has both a real part and an imaginary part. For example, if you want to solve
::有时当您解开二次方程时, 解决方案既包含真实部分, 也包含假想部分。 例如, 如果您想要解开

播放段落

$\begin{align*}(x - 1)^2 + 4 = 0\end{align*}$
:x-1)2+4=0

播放段落

then
::时当时

播放段落

$\begin{align*}(x - 1)^2 = -4\end{align*}$
:x-1)24

播放段落

$\begin{align*}x - 1 = \pm\sqrt{-4}\end{align*}$
::x-14

播放段落

$\begin{align*}x - 1 = \pm\sqrt{-1}\sqrt{4}\end{align*}$
::x-114

播放段落

$\begin{align*}x - 1 = \pm2i\end{align*}$
::x-12i

播放段落

$\begin{align*}x = 1 \pm 2i\end{align*}$
::x=12i

播放段落

$\begin{align*}x = 1 + 2i\end{align*}$ or $\begin{align*}1 - 2i\end{align*}$
::x=1+2ior1-2i x=1+2ior1-2i

播放段落

Notice that these two solutions involve a real part, 1, and an imaginary part, ±2 i
::请注意,这两种解决办法都包含一个真正的部分,一个是第1部分,一个是假想的一部分, 2i

播放段落

a + bi is the standard or rectangular form of a complex number .
::a + 双是复数的标准或矩形。

播放段落

A complex number is a number that has a real part (in this case a ) and an imaginary part, that is, the i with a coefficient b .
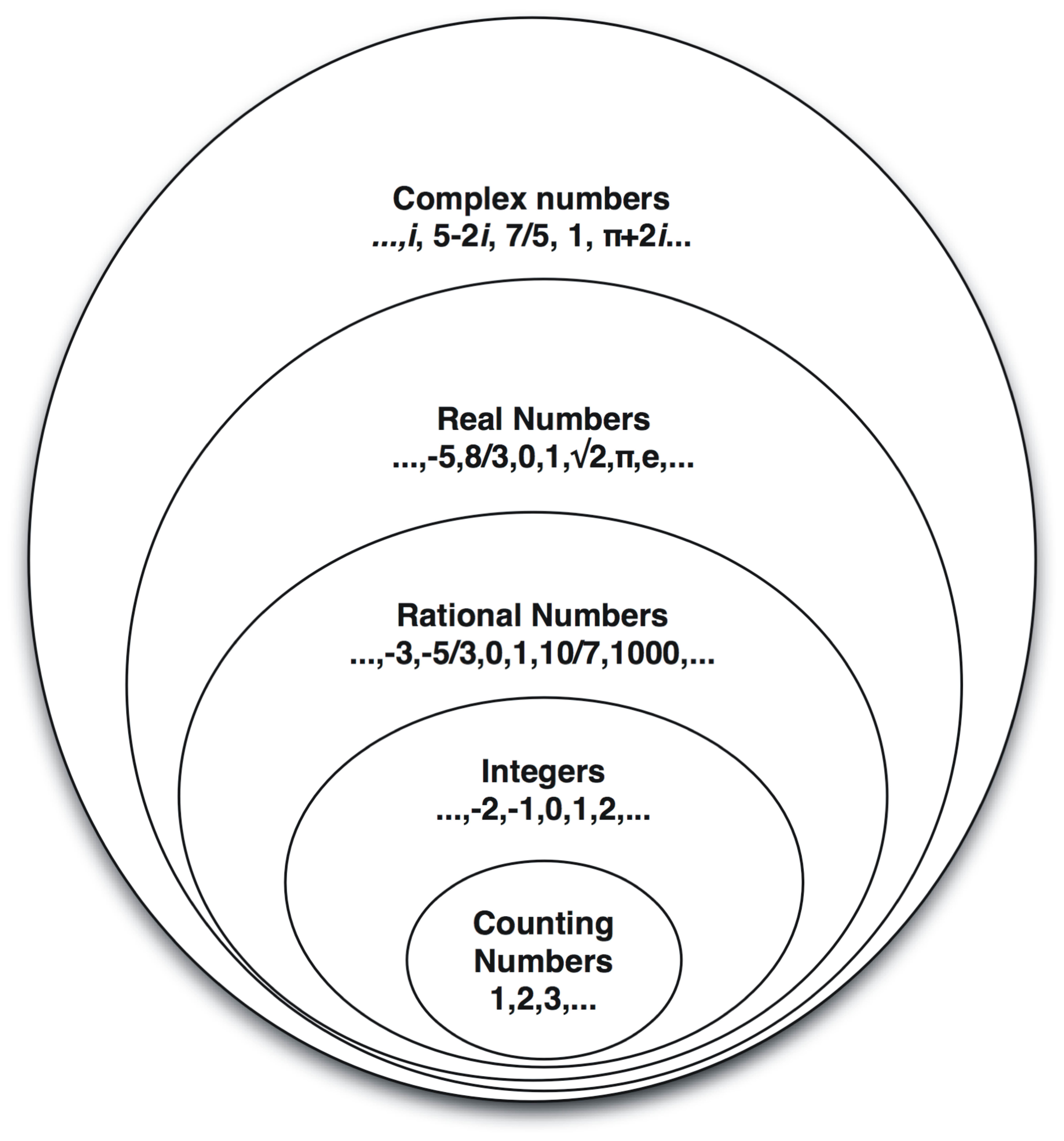
::复数是一个具有真实部分(在本案中a)和想象部分(即具有系数b的i)的数字。

播放段落

are a superset of the real numbers, meaning that all of the real numbers are part of the set of complex numbers:
::是一个真实数字的超级, 这意味着所有真实数字都是一组复杂数字的一部分:

播放段落

Given a + bi , if b = 0 (meaning there is no imaginary part to the complex number), then all you have remaining is a real number. Viewed this way, every real number can be written as a complex number (just let it equal a ), but there are many more complex numbers than real numbers. Hence the complex numbers are a superset of the real numbers.
::以 + 双 表示, 如果 b = 0( 意思是复数中没有虚构的部分) , 那么您所剩的只是一个真实的数字。 从这个角度看, 每个真实的数字都可以写成一个复杂的数字( 让它等于 a ) , 但数字比实际数字复杂得多。 因此, 复杂的数字是真实数字的超集 。

播放段落

Graphing Complex Numbers
::图形综合数字

播放段落

In standard form, a + bi , a complex number can be graphed using rectangular coordinates ( a , b ). The x - coordinate represents “real number” values, while the y - coordinate represents the “imaginary” values.
::在标准格式, + 双, 复数可以使用矩形坐标(a, b) 绘制图表。 x - 坐标代表“实际数字”值, Y - 坐标代表“想象”值。

播放段落

Examples
::实例

播放段落

Example 1
::例1

播放段落

Earlier, you were asked a question about which direction you move when you graph .
::早些时候,有人问过您在图形中移动的方向 。

播放段落

You of course don't  only imagine moving in one direction!
::当然,你不仅想象着向一个方向前进!

播放段落

When graphing complex numbers in standard form: a + bi , the real component a is plotted on the horizontal or x axis. The imaginary component bi is plotted on the y axis in just the same way a real number would be.
::当以标准格式绘制复合数字时: + 双形, 一个真实的元件是在水平轴或 x 轴上绘制的。 想象的元件双形以与实际数字相同的方式在 y 轴上绘制。

播放段落

$\begin{align*}\therefore 4 + 3i\end{align*}$ would be located 4 units to the right and 3 units up from the origin.
::4+3i将位于右边4个单元,从原产地往上3个单元。

播放段落

Example 2
::例2

播放段落

Graph the complex number: z = 2 + 2 i , in rectangular form .
::复数图:z = 2 + 2i, 矩形。

播放段落

The coordinate (2, 2) is graphed as shown below:
::坐标(2,2)如下图所示:

播放段落

Example 3
::例3

播放段落

Solve each equation and express it as a complex number. (Note: If the imaginary part is 0, express the solution as a + 0i )
:注:如果想象部分为0,则将溶液表示为+ 0i)

播放段落
1. x ² + 24 = 0
   ::x2+24=0

播放段落

$\begin{align*}x = \pm2\sqrt{6}i\end{align*}$
::x26i

播放段落
2. 2 x ² - 4 x + 7 = 0
   ::2x2 - 4x+7=0

播放段落

$\begin{align*}x = 1 \pm 2\sqrt{3}i\end{align*}$
::x=123i

播放段落

Example 4
::例4

播放段落

Plot each of the following complex numbers in rectangular form:
::以矩形形式绘制下列复杂数字的每一个:

播放段落
1. (4 + 2 i )
   :4+2)(一)
播放段落
2. (-3 + i )
   :-3+一)
播放段落
3. (3 - 4 i )
   :3-4)(一)
播放段落
4. 3 i
   ::3i 3i

播放段落

Your graph should look like:
::您的图表应该看起来像 :

播放段落

Example 5
::例5

播放段落

Simplify and express as a complex number $\begin{align*}-\sqrt{60} + \sqrt{-121}\end{align*}$ .
::简化和表达复杂编号-60121。

播放段落

$\begin{align*}-\sqrt{4 \cdot 15} + \sqrt{121 \cdot -1}\end{align*}$ Factor the numbers under the roots
::- 415+1211 根下数字乘数

播放段落

$\begin{align*}-2\sqrt{15} + 11\sqrt{-1}\end{align*}$ Simplify the perfect square roots
::- 215+11-1 简化完美的平方根

播放段落

$\begin{align*}-2\sqrt{15} + 11i\end{align*}$
::- 215+11i

播放段落

Example 6
::例6

播放段落

Solve the equation and express the answer as a simplified complex number $\begin{align*}x(4x) + 4 = 0\end{align*}$ .
::解析方程, 并用简化的复合号 x( 4x)+4=0 表示答案 。

播放段落

$\begin{align*}4x^2 + 4 = 0\end{align*}$ Distribute the x
::4x2+4=0 分配 x

播放段落

$\begin{align*}4x^2 = -4\end{align*}$ Subtract 4 from both sides
::4x24 双方减4

播放段落

$\begin{align*}x^2 = -1\end{align*}$ Divide both sides by 4
::x21 双方除以 4

播放段落

$\begin{align*}x = i\end{align*}$ Take the square root of both sides
::x=i 取两侧的平方根

播放段落

Example 7
::例7

播放段落

Graph the complex numbers:
::图形复合数字 :

播放段落
1. 3 + 2i
   ::3+2i 3+2i
播放段落
2. 2 - 3i
   ::2-3i 2 - 3i
播放段落
3. -2 + 2i
   ::-2+2i+2i

播放段落

To graph the complex numbers, graph the real value on the x axis, and the imaginary value on the y axis. The image below shows the points correctly graphed.
::要绘制复杂数字图,请绘制 x 轴上的真实值图,以及 y 轴上的假想值图。下面的图像显示正确绘制的点。

播放段落

Review
::回顾

播放段落
1. What are complex numbers technically the sum of?
   ::从技术上讲,什么是复杂数字的总和?
播放段落
2. What does the complex plane represent?
   ::复杂的飞机代表什么?

播放段落

Express in simplest form in terms of $\begin{align*}i\end{align*}$ .
::以最简单的形式,以i表示。

3. $\begin{align*}13 - \sqrt{-49}\end{align*}$
4. $\begin{align*}\sqrt{75} + \sqrt{\frac{-16}{256}}\end{align*}$
5. $\begin{align*}-3 - \sqrt{\frac{-25}{169}}\end{align*}$
6. $\begin{align*}-\sqrt{36} + \sqrt{-64}\end{align*}$
7. $\begin{align*}10 - \sqrt{\frac{-4}{36}}\end{align*}$
8. $\begin{align*}4 + \sqrt{-250}\end{align*}$
9. $\begin{align*}3^2 \sqrt{-0.0009}\end{align*}$
10. $\begin{align*}\sqrt{-0.16} -(- \sqrt{27})\end{align*}$
11. $\begin{align*}10 + \sqrt{-0.49}\end{align*}$
12. $\begin{align*}-3 + \sqrt{-0.0196}\end{align*}$
播放段落
13. $\begin{align*}9 \sqrt{-8j^9} + 3\sqrt{25}\end{align*}$
    ::9-8日9+325
播放段落
14. $\begin{align*}\sqrt{-676b^3a^1c^8} +\sqrt{112}\end{align*}$
    ::- 676b3a1c8+112

播放段落
15. Two complex numbers are graphed below. What are the numbers expressed in standard complex number form?
    ::下面以图表形式列出两个复杂数字。标准复杂数字表显示的数字是多少?

播放段落
16. Graph the complex number $\begin{align*}3 - 4i\end{align*}$ .
    ::3-4i号复合体图。
播放段落
17. Graph the complex number $\begin{align*}-2 + 3i\end{align*}$ .
    ::复数-2+3i 图形。
播放段落
18. Graph the complex point $\begin{align*}(3 + i)\end{align*}$ .
    ::绘制复合点(3+i)的图。
播放段落
19. Graph the complex point $\begin{align*}(-1 - 2i)\end{align*}$ .
    ::复杂点(-1-2i)的图解。

播放段落

Review (Answers)
::回顾(答复)

播放段落

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。