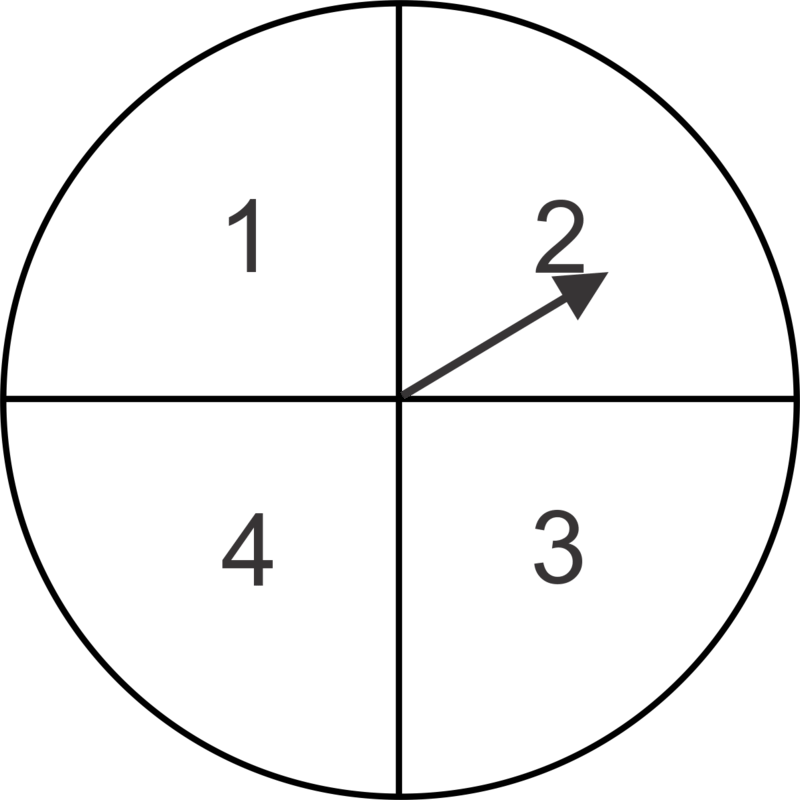Section: 计算联合活动的概率 | 12.9 计算联合活动的可能性

Section outline

A snack bag of animal crackers contains 5 elephants, 7 monkeys, and 4 lions. What is the probability that the first two crackers you randomly pull from the bag will be a lion followed by an elephant?
::一袋动物饼干包含5只大象、7只猴子和4只狮子。你随机从袋子中抽取的头两只饼干,有一只狮子跟随大象的几率有多大?

Probabilities of Combined Events
::联合活动的可能性

When multiple events occur we can calculate the probability of these combined events by finding their product if the events are independent. are events for which the outcome of one event does not affect the outcome of a second event. For example, if we roll a die and then roll it again, the outcome of the second roll is independent from the outcome of the first event.
::当发生多个事件时, 我们可以通过找到这些合并事件的产物来计算这些合并事件的概率, 如果事件是独立的。它们是一个事件的结果不影响第二个事件的结果的事件。例如, 如果我们滚动一个死亡然后再次滚动它, 第二卷的结果独立于第一个事件的结果。

To determine the probability of two independent events, $\begin{aligned} A \end{aligned}$ and $\begin{aligned} B \end{aligned}$ , both occurring, we multiply the probabilities of each of the two events together: $\begin{aligned} P (A) \times P (B) = P (A a n d B) \end{aligned}$ .
::为了确定发生两个独立事件(A和B)的概率,我们将两个事件(P(A)xxP(B)=P(A和B))的概率乘以两个事件(P(A)xxP(B)=P(A和B))的概率。

In some cases, the outcome of one event affects the outcome of a second event. For example, when a hand of cards is dealt in a game of poker, the probability of receiving a particular card changes based on what cards have already been dealt. This is an example of . We will introduce conditional probability here for situations in which we can manipulate the subsequent probabilities to make independent events as shown in problem 3 below .
::在某些情况下,一个事件的结果会影响第二个事件的结果。例如,在扑克牌游戏中处理牌手的情况,根据牌牌已经处理过的情况,收到特定卡片变动的概率。这是一个例子。我们将在此引入有条件的概率,以说明我们可以操纵随后的概率,使下文问题3所显示的独立事件成为独立事件的情况。

Let's solve the following problems.
::让我们解决以下的问题。

Given a fair die and a fair coin, find the following probabilities.
::如果有一个公平的死亡和一个公平的硬币, 找到以下的概率。

rolling a 5 and getting tails.
::5号滚动尾巴也跟着

rolling an odd number and getting heads.
::滚动一个奇数并获得头部。

Since the outcome of rolling the die does not affect the outcome of flipping the coin, these are independent events. Thus we can determine their individual probabilities and multiply them together.
::由于滚动死亡的结果并不影响翻转硬币的结果,这些是独立事件,因此我们可以确定它们各自的概率,并一起乘以它们。

$\begin{aligned} P (5) \times P (T) = \frac{1}{6} \times \frac{1}{2} = \frac{1}{12} \end{aligned}$
::P(5)xP( T) = 16x12= 112

$\begin{aligned} P (1, 3, 5) \times P (H) = \frac{3}{6} \times \frac{1}{2} = \frac{3}{12} = \frac{1}{4} \end{aligned}$
::P(1,3,5,6)xP(H)=36x12=312=14

What is the probability of rolling doubles twice in a row? Three times in a row?
::连续两次滚动双倍的概率是多少? 连续三次滚动双倍的概率是多少?

Each of these rolls are independent events. It is human nature to think that just because we have rolled doubles once or twice already that we are unlikely to roll them another time. It is true that that probability of rolling doubles three times in a row is smaller than rolling doubles once but this is not because the probability changes for each roll. Let’s look at why this occurs:
::这些卷卷都是独立的事件。仅仅因为我们已经翻了一倍或两倍,所以我们不可能再翻一次。诚然,每行翻了三次的概率比一次翻两次的概率要小,但这并非因为每卷的概率变化。让我们看看为什么会发生这种情况:

$\begin{aligned} P (doubles) = \frac{6}{36} = \frac{1}{6} \end{aligned}$ , since there are six ways to roll doubles.
::P(双倍)=636=16,因为有六种方法可以翻倍。

$\begin{aligned} P (doubles twice) = \frac{1}{6} \times \frac{1}{6} = \frac{1}{36} \end{aligned}$
::P(双倍)=16x16=136

$\begin{aligned} P (doubles three times) = \frac{1}{6} \times \frac{1}{6} \times \frac{1}{6} = \frac{1}{216} \end{aligned}$
::P( 双倍三次) = 16x16x16= 1216

What is the probability that you draw an ace from a deck of cards three times if each card is replaced before the next card is drawn? What if each card is not replaced?
::如果每张牌在下一张卡片之前被替换三次,那么从牌牌牌牌上抽取一张A的概率是多少?如果每张卡片没有被替换,则如何?

There are 4 aces in a deck of cards, so there is a $\begin{aligned} \frac{4}{52} = \frac{1}{13} \end{aligned}$ chance of drawing an ace each time a card is selected. For the first part of the question which requires each card chosen to be replaced, the probability of selecting an ace does not chance so the events are independent of one another.
::牌牌牌牌牌有4张A, 所以每选一张牌, 就有452=113个机会绘制一张A。对于问题第一部分, 每选一张牌都要被替换, 选择一张A的可能性并不大, 所以事件会彼此独立。

$\begin{aligned} P (three aces, with replacement) = {(\frac{1}{13})}^{3} = \frac{1}{2197} \end{aligned}$ .
::P(三A,替换)=(113)3=12197。

The second part of the question does not require replacement. Now the events are not strictly independent. We can, however, determine the probability of an independent event and use multiplication to find the probability of the combined events. For the first selection, there are 4 aces in the 52 card deck. After an ace is selected, how many cards remain? Well, to determine the probability of selecting three aces, we must assume the first selected was an ace so now there are 3 aces remaining in a deck of 51 cards. After the second ace is selected, there are 2 aces in a deck of 50 cards. Now we can find the product of these probabilities.
::问题第二部分不需要替换。现在事件并不严格独立。但是, 我们可以确定独立事件的概率, 并使用乘数来查找合并事件的概率。对于第一个选择, 52 张牌有 4 张A 。在选择一张牌后, 有多少张卡还存在? 那么, 为了确定选择三张A 的概率, 我们必须假设第一个选择的A 是一张A, 现在51张牌的甲牌中还剩下三张A。在选择第二个 A 牌后, 甲牌有两张A 。现在我们可以找到这些概率的产物。

$\begin{aligned} P (three aces, without replacement) = \frac{4}{52} \times \frac{3}{51} \times \frac{2}{50} = \frac{1}{13} \times \frac{1}{17} \times \frac{1}{25} = \frac{1}{5525} \end{aligned}$ .
::P(三A,无替换)=452×351×250=113×117×125=15525。

Notice that the probability of selecting an ace diminishes with each selection in this situation because the number of aces in the deck is being reduced.
::请注意,在这种情况下,由于甲板中的A数正在减少,选择A的概率随着每次选择而降低。

Examples
::实例

Example 1
::例1

Earlier, you were asked to find the probability that the first two crackers you randomly pull from the bag will be a lion followed by an elephant.
::早些时候,你被要求找到的可能性前两个饼干你随机抽取从袋子中抽取将是狮子跟着大象。

There are $\begin{aligned} 7 + 5 + 4 = 16 \end{aligned}$ crackers in the bag. The probability that the first cracker you pull will be a lion will therefore be $\begin{aligned} \frac{4}{16} = \frac{1}{4} \end{aligned}$ .
::袋子里有7+5+4=16饼干。因此, 你第一次拉的饼干是狮子的概率是 416=14。

Now there are 15 crackers remaining in the bag, so the probability that the second cracker you pull from the bag will be an elephant is $\begin{aligned} \frac{5}{15} = \frac{1}{3} \end{aligned}$ .
::现在袋子里还剩15个饼干所以从袋子里拉出来的第二个饼干可能是大象515=13

Finally, $\begin{aligned} P (lion followed by elephant, without replacement) = \frac{1}{4} \times \frac{1}{3} = \frac{1}{12} \end{aligned}$ .
::最后,P(一升后为大象,无替换)=14x13=112。

Determine the following probabilities.
::确定下列概率。

Example 2
::例2

Rolling snake eyes (double ones) and then rolling a sum of seven on a pair of dice.
::双眼滚动,双眼滚动,然后在一对骰子上滚动七分之七。

$\begin{aligned} P (snake eyes) \times P (seven) = \frac{1}{36} \times \frac{1}{6} = \frac{1}{216} \end{aligned}$ .
::P( snake eyes) xP( 7) =136x16=1216。

Example 3
::例3

Turning over a face card (jack, queen or king) followed by an ace from a full, shuffled deck of cards.
::翻过一张脸牌(杰克、王后或王牌),然后是一张牌牌全牌牌的A。

$\begin{aligned} P (jack, queen, king) \times P (ace) = \frac{12}{52} \times \frac{4}{51} = \frac{4}{221} \end{aligned}$
::P( 杰克、皇后、王) ×P( 冰) = 1252x451= 4221

Example 4
::例4

Drawing a hand of five cards which contains exactly 2 jacks, from a full, shuffled deck of cards.
::画一张五张牌的手, 里面有两张J, 从一张满满的打乱的牌牌牌牌上抽出来。

$\begin{aligned} P (jack) \times P (jack) \times P (non jack) \times P (non jack) \times P (non jack) = \frac{4}{52} \times \frac{3}{51} \times \frac{48}{50} \times \frac{47}{49} \times \frac{46}{48} = \frac{1081}{270725} \approx 0.00399298 \end{aligned}$
::P( 抓) ×P( 抓) ×P( 不抓) ×P( 不抓) ×( 不抓) ×( 不抓) ×( 不抓) ×( 抓) ×( 不抓) ×( 抓) ×( 抓) ×( 抓) ×( 抓) ×( 抓) ×( 抓) ×( 抓) ×( 抓) ×( 抓) ×( 抓) ×( 抓) ×( 抓) ×( 抓) ×( 不抓) ×( 抓) ×351×4850 ×4749} }}}}4648= 1081270725 0.00399298

We aren’t quite finished, however, because what we have determined here is the probability that the first two cards are the jacks and the last three are the non jacks. These cards could have been dealt in any order so we need to determine the number of permutations of these cards and multiply by that value . Keep in mind that the jacks are “non distinguishable” and the non jacks are “non distinguishable”. The permutations are: $\begin{aligned} \frac{5!}{2! 3!} = 10 \end{aligned}$ . This could also be described as the number of combinations of selecting two jacks from a set of five cards: $\begin{aligned} _{5} C_{2} = \frac{5!}{2! (5 - 2)!} = 10 \end{aligned}$ . These are just two ways to find the same result. Now that we have the number of combinations or arrangements, we can multiple our probability by this value:
::然而,我们还没有完全完成, 因为我们在这里确定的是, 前两张牌的概率是杰克, 最后三张是非杰克。这些卡可以按任何顺序处理, 所以我们需要确定这些卡的变异数, 并乘以这个数值。记住, 杰克是“ 无法区分的 ” , 非杰克是“ 无法区分的 ” 。变异是 : 5! 2! 3! = 10。这也可以被描述为从一套五张卡中选择两张J的组合数 : 5C2=5! 2! (5- 2)! =10。这些只是找到相同结果的两种方法。现在我们有了组合或安排的数目, 我们可以乘以这个数值的概率 :

$\begin{aligned} \frac{1081}{270725} \times 10 \approx 0.0399298181 \end{aligned}$ .

Example 5
::例5

Randomly selecting a pair of black socks followed by a pair of navy blue socks and then a pair of white socks from a drawer containing 5 black pairs, 4 navy blue pairs and 8 white pairs if each selection is replaced before the next pair is chosen. What if each pair is not replaced?
::随机选择一对黑袜子,然后从抽屉里挑选一对海军蓝袜子,然后从5对黑袜子,4对海军蓝袜子和8对白袜子,如果在选择下一对黑袜子之前替换了每对黑袜子,那么,如果每对白袜子没有被替换呢?

For the first part of the question, the total number of socks in the drawer remains the same for each selection, 17. So, $\begin{aligned} P (black, then blue, then white) = \frac{5}{17} \times \frac{4}{17} \times \frac{8}{17} = \frac{160}{4913} \approx 0.032567 \end{aligned}$ . Now, if we do not replace the socks, the number of socks decreases with each sock selected: $\begin{aligned} P (black, then blue, then white) = \frac{5}{17} \times \frac{4}{16} \times \frac{8}{15} = \frac{160}{4080} = \frac{2}{51} \approx 0.039216 \end{aligned}$ . This probability is slightly higher because removing one pair of black socks makes it more likely that we will select a different color pair of socks for the next pair and so on.
::对于问题的第一部分,抽屉中的袜子总数在每个选择区保持不变,17。所以,P(黑色,然后是蓝色,然后是白色)=517×417×817=16049130.032567. 如果我们不更换袜子,袜子数量会随着所选每只袜子而减少:P(黑色,然后是蓝色,然后是白色)=517×416×815=1604080=2510.039216. 这个概率略高一点,因为除去一双黑袜子,我们更有可能为下一对袜子选择另一双色袜子,等等。

Review
::回顾

Given a spinner as shown in the illustration below, two fair six sided dice and a standard deck of 52 playing cards, calculate the probability of each compound event below.
::鉴于下面插图所示的旋翼,两张六面骰子和一张52张牌的标准甲板,计算下方每场复合事件的概率。

Spin a 4 and roll doubles.
::旋转一个4,滚动双倍。

Spin an odd number and roll an odd sum.
::转一个奇数转一个奇数

Draw four red cards in a row without replacement.
::连续绘制四张红卡片,不替换。

Draw three face cards (jack, queen, king) without replacement.
::绘制三张脸牌(杰克、皇后、国王),

Rolling a sum of eight and spinning a 2.
::滚动了8个和转动了2个

Spin a three, three times in a row.
::连续旋转三三次

Roll an even sum and spin a prime number.
::滚动一个偶数和旋转一个质数。

Draw a five card hand containing exactly 3 red and 2 black cards.
::画一张五张纸牌手牌里面有3张红牌和2张黑卡

Draw a five card flush (a hand in which all cards are the same suit).
::绘制五张牌牌( 一张牌都是同一套西装的手) 。

Draw a hand of five cards containing exactly two hearts.
::绘制五张卡片的手, 里面有两张红桃。

Draw a hand of three cards that contains at least one spade.
::绘制三张卡片的手, 其中至少包含一个平方块。

Roll a sum of 7 or 11 and draw three cards in which at least one is a face card.
::滚动总和为7或11,并抽出三张卡片,其中至少一张是一张脸卡。

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

Section outline

Probabilities of Combined Events ::联合活动的可能性

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

Example 5 ::例5

Review ::回顾

Review (Answers) ::回顾(答复)

Probabilities of Combined Events
::联合活动的可能性

Examples
::实例

Example 1
::例1

Example 2
::例2

Example 3
::例3

Example 4
::例4

Example 5
::例5

Review
::回顾

Review (Answers)
::回顾(答复)