Section: 基本几何概率 | 12.11 基本几何概率

Section outline

A rectangular dartboard that measures 12 inches by 24 inches has a 2-inch by 2-inch red square painted at its center. What is the probability that a dart that hits the dartboard will land in the red square?
::以 12 英寸乘 24 英寸测量 12 英寸的矩形飞镖板在其中心涂上 2 英寸乘 2 英寸的红色方形。撞击飞镖的飞镖在红方方形降落的概率有多大 ?

Geometric Probabilities
::几何概率

Sometimes we need to use our knowledge of geometry to determine the likelihood of an event occurring. We may use areas, volumes, angles, polygons or circles.
::有时我们需要利用我们对几何学的知识来确定发生事件的可能性。我们可以使用区域、数量、角度、多边形或圆圈。

Let's s olve the following problems.
::让我们解决以下的问题。

A game of pin-the-tale-on-the-donkey has a rectangular poster that is 2ft by 2ft. The area in which the tale should be pinned is shown as a circle with radius 1 inch. Assuming that the pinning of the tale is completely random and that it will be pinned on the poster (or the player gets another try), find the probability of pinning the tale in the circle?
::平面图纸游戏的矩形海报是 2 英尺乘以 2 英尺。故事应该被固定的区域以圆形显示为圆形, 半径为 1 英寸。假设故事是完全随机的, 并且会被钉在海报上( 或者玩家再试一次) , 找到将故事钉在圆圈里的概率吗 ?

This probability can be found by dividing the area of the circle target by the area of the poster. We must have the same units of measure for each area so we will convert the feet to inches.
::此概率可以通过将圆形目标区域除以海报区域来找到。我们必须为每个区域设定相同的度量单位, 以便将脚转换为英寸。

$\begin{aligned} \frac{1^{2} π}{24^{2}} \approx 0.005454 o r about 0.5 % chance . \end{aligned}$

::12 2420.005454 或大约0.5%的机会。

In a game of chance, a pebble is dropped onto the board shown below. If the radius of each of blue circle is 1 cm, find the probability that the pebble will land in a blue circle.
::在一场偶然游戏中, 将一块石块投放到下面显示的棋盘上。如果每块蓝色圆的半径为 1 厘米, 请找到这个石块在蓝色圆圈中降落的概率。

The area of the square is $\begin{aligned} 16 c m^{2} \end{aligned}$ . The area of each of the 16 circles is $\begin{aligned} 1^{2} π = π \end{aligned}$ . The probability of the pebble landing in a circle is the sum of the areas of the circles divided by the area of the square.
::方块面积为16厘米。 16个圆圈中每个圆圈的面积为12英寸。方块降落在圆圈中的概率是圆圈区域除以方块的面积的总和。

$\begin{aligned} P (blue circle) = \frac{16 π}{64} \approx 0.785 \end{aligned}$
::P( 蓝色圆圈) = 16_ 64_ 0. 785

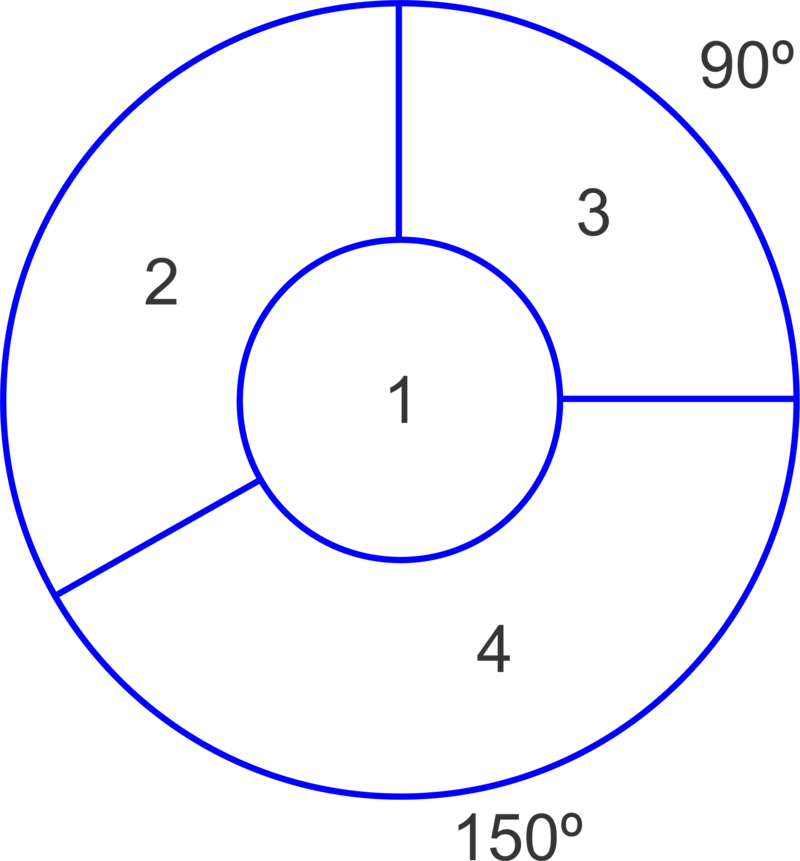
What is the probability that a randomly thrown dart will land in a red area on the dart board shown? What is the probability that exactly two of three shots will land in the red? The radius of the inner circle is 1 unit and the radius of each annulus is 1 unit as well.
::随机投射的飞镖在显示的飞镖板上的红色区域着陆的概率是多少?三发子弹中的两发会投入红色的概率是多少?内圆的半径是1个单位,每个失效装置的半径也是1个单位。

First we need to determine the probability of landing in the red. There are four rings of width 1 and the radius of the center circle is also 1 so the total radius is 5 units. The area of the whole target is thus $\begin{aligned} 25 π \end{aligned}$ square units. Now, we need to find the areas of the two red rings and the red circular center. The center circle area is $\begin{aligned} π \end{aligned}$ square units. The outside ring area can be found by subtracting the area inside from the entire circle’s area. The inside circle will have a radius of 4 units, the area of the outer ring is $\begin{aligned} 25 π - 16 π = 9 π \end{aligned}$ square units. This smaller red ring’s area can be found similarly. The circle with this red ring on the outside has a radius of 3 and the circle inside has a radius of 2 so, $\begin{aligned} 9 π - 4 π = 5 π \end{aligned}$ square units. Finally, we can add them together to get the total red area and divide by the area of the entire target. $\begin{aligned} \frac{9 π + 5 π + π}{25 π} = \frac{15 π}{25 π} = \frac{3}{5} \end{aligned}$ . So the probability of hitting the red area is $\begin{aligned} \frac{3}{5} \end{aligned}$ or 60%.
::首先,我们需要确定红色降落的概率。有四圈宽度 1, 中间圆的半径是 1, 这样整个半径是 5 个单位。整个目标区域是 25 平方单位。现在我们需要找到两个红环和红圆中心的区域。中间圆区域是 + 平方单位。外部环区域是 4 个单位 , 外环区域是 25 16 9 平方单位。这个较小的红环区域也同样可以找到。外环区域是 3 的半径 3 , 内部圆的半径是 9 4 5 5 平方单位。最后, 我们可以把它们加在一起, 以获得整个目标区域的红区域。 9 5 25 15 15 25 35 。因此, 红环的面积概率是 35 或 60 。

For the second part of the problem we will use a binomial probability. There are 3 trials, 2 successes and the probability of a success is 0.6: $\begin{aligned} (\binom{3}{2}) (0.6)^{2} (0.4) = 0.432 \end{aligned}$
::对于问题的第二部分,我们将使用二元概率。有3个试验,2个成功,成功概率为0.632)(0.6)(2(0.4)=0.432)

Examples
::实例

Example 1
::例1

Earlier, you were asked to find the probability that a dart that hits the dartboard will land in the red square.
::早些时候,有人要求你找到一个飞镖击中飞镖降落在红色广场的概率

This probability can be found by dividing the area of the red square by the area of the dartboard. The area of the dartboard is $\begin{aligned} 12 \times 24 = 288 \end{aligned}$ . The area of the red square is $\begin{aligned} 2 \times 2 = 4 \end{aligned}$ . Therefore, the probability of the dart landing in the red square is
::通过将红方的区域除以 dartboard 区域来找到此概率。 dartboard 区域为 12x24=288. 红方区域为 2x2= 4。因此, 飞镖在红方中着陆的概率为 12x24=288 。

$\begin{aligned} \frac{4}{288} \\ \frac{1}{72} \\ \approx 0.0139 \end{aligned}$

Therefore, there is about a 1.39% chance the dart will hit the red square.
::因此,有1.39%的概率飞镖会击中红方形

Example 2
::例2

Consider the picture below. If a “circle” is randomly chosen, what is the probability that it will be:
::如果随机选择一个“圆圈”,那么其概率是:

red
::红色红

$\begin{aligned} \frac{29}{225} \end{aligned}$

yellow
::黄黄色

$\begin{aligned} \frac{69}{225} \end{aligned}$

blue or green
::蓝色或绿色

$\begin{aligned} \frac{84}{225} \end{aligned}$

not orange
::非橙色

$\begin{aligned} \frac{182}{225} \end{aligned}$

Example 3
::例3

If a dart is randomly thrown at the target below, find the probability of the dart hitting in each of the regions and show that the sum of these probabilities is 1. The diameter of the center circle is 4 cm and the diameter of the outer circle is 10 cm. What is the probability that in 5 shots, at least two will land in the 4 region?
::如果飞镖随机投向下面的目标,发现每个区域的飞镖撞击概率,并显示这些概率的总和是1。中心圆的直径是4厘米,外圆的直径是10厘米。在5发子弹中,至少有2发子弹将降落在4个区域,概率是多少?

$\begin{aligned} P (1) & = \frac{2^{2} π}{5^{2} π} = \frac{4}{25} \\ P (2) & = \frac{120}{360} (\frac{5^{2} π - 2^{2} π}{5^{2} π}) = \frac{1}{3} \times \frac{21 π}{25 π} = \frac{7}{25} \\ P (3) & = \frac{90}{360} (\frac{5^{2} π - 2^{2} π}{5^{2} π}) = \frac{1}{4} \times \frac{21 π}{25 π} = \frac{21}{100} \\ P (4) & = \frac{150}{360} (\frac{5^{2} π - 2^{2} π}{5^{2} π}) = \frac{5}{12} \times \frac{21 π}{25 π} = \frac{35}{100} \end{aligned}$

::P(1)=2252425P(2)=120360(522225)=13x21_25}725P(3)=90360(522252)=14x21}25}21100P(4)=150360(522252)=512x21}25}35}100

Now add them up:
::现在加起来:

$\begin{aligned} P (1) + P (2) + P (3) + P (4) = \\ = \frac{4}{25} + \frac{7}{25} + \frac{21}{100} + \frac{35}{100} \\ = \frac{16}{100} + \frac{28}{100} + \frac{21}{100} + \frac{35}{100} \\ = \frac{100}{100} = 1 \end{aligned}$

::P(1)+P(2)+P(3)+P(3)+P(4)=425+725+21100+35100=16100+28100+21100+35100=100100=1

The probability of landing in region 4 at least twice in five shots is equivalent to $\begin{aligned} 1 - [P (0) + P (1)] \end{aligned}$ .
::在区域4上岸的概率至少是五发中的两次,相当于1-[P(0)+P(1)]。

Use binomial probability to determine these probabilities:
::使用二进制概率来确定这些概率:

$\begin{aligned} 1 - [(\binom{5}{0}) {(\frac{35}{100})}^{0} {(\frac{65}{100})}^{5} + (\binom{5}{1}) {(\frac{35}{100})}^{1} (\frac{65}{100}) 4] \\ = 1 - (0.116029 + 0.062477) \\ \approx 0.821 \end{aligned}$

Review
::回顾

Use the diagram below to find the probability that a randomly dropped object would land in a triangle of a particular color.
::使用下图查找随机投落的物体在特定颜色的三角形下着陆的概率。

yellow
::黄黄色

green
::绿绿色

plum
::李子

not yellow
::非黄色

not yellow or light blue
::不是黄色或浅蓝色

The dart board to the right has a red center circle (bull’s eye) with area $\begin{aligned} π c m^{2} \end{aligned}$ . Each ring surrounding this bull’s eye has a width of 2 cm. Use this information to answer the following questions.
::公牛右侧的飞镖板有一个红心圆(bull's eye),区域为 cm2。环绕公牛眼睛的每个环宽度为 2 厘米。使用此信息回答下列问题。

Given a random throw of a dart, what is the probability that it will land in a white ring?
::如果有飞镖随意投出飞镖在白环上降落的概率是多少?

What is the probability of a bull’s eye?
::牛眼的概率是多少?

What is the probability that in 10 throws, exactly 6 land in the black regions?
::在10个投球中黑区6个土地的概率是多少?

What is the probability that in 10 throws, at least one will land in the bull’s eye?
::在10次投球中,至少有1次投在公牛眼中的可能性有多大?

How many darts must be thrown to have a 95% chance of making a bull’s eye?
::有多少飞镖必须投出 95% 的机会使公牛的眼睛?

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

Section outline

Geometric Probabilities ::几何概率

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Review ::回顾

Review (Answers) ::回顾(答复)

Geometric Probabilities
::几何概率

Examples
::实例

Example 1
::例1

Example 2
::例2

Example 3
::例3

Review
::回顾

Review (Answers)
::回顾(答复)